К написанию статьи подтолкнул вот этот комментарий. А точнее, одна фраза из него.
… расходовать память или такты процессора на элементы в миллиардных объёмах — это нехорошо…Так сложилось, что в последнее время мне именно этим и пришлось заниматься. И, хотя, случай, который я рассмотрю в статье, довольно частный — выводы и применённые решения могут быть кому-нибудь полезны.
Немного контекста
Приложение iFunny имеет дело с колоссальным объёмом графического и видеоконтента, а нечёткий поиск дубликатов является одной из очень важных задач. Сама по себе это большая тема, заслуживающая отдельной статьи, но сегодня я просто немного расскажу о некоторых подходах к обсчёту очень больших массивов чисел, применительно к этому поиску. Конечно же, у всех разное понимание «очень больших массивов», и тягаться с Адронным коллайдером было бы глупо, но всё же. :)
Если совсем коротко про алгоритм, то для каждого изображения создаётся его цифровая подпись (сигнатура) из 968 целых чисел, а сравнение производится путем нахождения «расстояния» между двумя сигнатурами. Учитывая, что объём контента только за два последних месяца составил порядка 10 миллионов изображений, то, как легко прикинет в уме внимательный читатель, — это как раз те самые «элементы в миллиардных объёмах». Кому интересно — добро пожаловать под кат.
В начале будет скучный рассказ про экономию тактов и памяти, а в конце небольшая поучительная история, про то, что иногда очень полезно смотреть в исходники. Картинка для привлечения внимания имеет прямое отношение к этой поучительной истории.
Должен признаться, что я немного слукавил. При предварительном анализе алгоритма удалось сократить количество значений в каждой сигнатуре с 968 до 420. Уже в два раза лучше, но порядок величин остался тот же.
Хотя, если подумать, то не так уж я и слукавил, и это будет первым выводом: прежде чем приступать к задаче, стоит подумать — а нельзя ли её как-то заранее упростить?
Алгоритм сравнения довольно простой: вычисляется корень из суммы квадратов разностей двух сигнатур, делится на сумму предварительно рассчитанных значений (т.е. в каждой итерации суммирование всё же будет и совсем его в константу не вынести) и сравнивается с пороговым значением. Стоит отметить, что элементы сигнатуры ограничены значениями от -2 до +2, а, соответственно, абсолютное значение разности — значениями от 0 до 4.
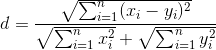
Ничего сложного, но количество решает.
Подход первый, наивный
// Порог
const val d = 0.3
// 10.000.000 объектов.
// Будем держать эту цифру в уме,
// чтобы не упоминать в каждом втором предложении
val collection: MutableList<Signature> = mutableListOf()
// signature — массив из 420 значений типа Byte
class Signature(val signature: Array<Byte>, val norma: Double)
fun getSimilar(signature: Signature) = collection
.filter { calculateDistance(it, signature) < d }
fun calculateDistance(first: Signature, second: Signature): Double =
Math.sqrt(first.signature.mapIndexed { index, value ->
Math.pow((value - second.signature[index]).toDouble(), 2.0)
}.sum()) / (first.norma + second.norma)
Давайте посчитаем, что у нас тут с количеством операций:
10M квадратных корней Math.sqrt10M сложений и делений / (first.norma + second.norma)4.200M вычитаний и возведений в квадрат Math.pow((value - second.signature[index]).toDouble(), 2.0)4.200M сложений .sum()Какие у нас есть варианты:
- При таких объёмах тратить целый
Byte(или, не дай бог, кто-то догадался бы использоватьInt) на хранение трёх значащих бит — это непростительное расточительство. - Может, как-то подсократить количество математики?
- А нельзя ли сделать какую-нибудь предварительную фильтрацию, не такую затратную по вычислениям?
Подход второй, упаковываем
Кстати, если кто-то предложит, как можно упростить вычисления при такой упаковке — получит большое спасибо и плюс в карму. Хоть и один, но зато от всей души :)
Один
Long — это 64 бита, что, в нашем случае, позволит хранить в нём 21 значение (и 1 бит останется неприкаянным).// массив из 20 значений типа Long
class Signature(val signature: Array<Long>, val norma: Double)
fun calculateDistance(first: Signature, second: Signature): Double =
Math.sqrt(first.signature.mapIndexed { index, value ->
calculatePartial(value, second.signature[index])
}.sum()) / (first.norma + second.norma)
fun calculatePartial(first: Long, second: Long): Double {
var sum = 0L
(0..60 step 3).onEach {
val current = (first.ushr(it) and 0x7) - (second.ushr(it) and 0x7)
sum += current * current
}
return sum.toDouble()
}
По памяти стало лучше (
4.200M против 1.600M байт, если грубо), но что там с вычислениями?Думаю, очевидно, что количество операций осталось прежним и к ним добавились
8.400M сдвигов и 8.400M логических И. Может и можно оптимизировать, но тенденция всё равно не радует — это не то, чего мы хотели.Подход третий, упаковываем заново с подвыподвертом
Нутром чую, тут можно использовать битовую магию!
Давайте хранить значения не в трёх, а в четырёх битах. Таким, вот, образом:
| -2 | 0b1100 |
| -1 | 0b0100 |
| 0 | 0b0000 |
| 1 | 0b0010 |
| 2 | 0b0011 |
Да, мы потеряем в плотности упаковки по сравнению с предыдущим вариантом, но зато получим возможность одним
XOR'ом получать Long с разностями (не совсем) сразу 16-ти элементов. Кроме того, будет всего 11 вариантов распределения бит в каждом конечном полубайте, что позволит использовать заранее рассчитанные значения квадратов разностей.// массив из 27 значений типа Long
class Signature(val signature: Array<Long>, val norma: Double)
// -1 для невозможных вариантов
val precomputed = arrayOf(0, 1, 1, 4, 1, -1, 4, 9, 1, -1, -1, -1, 4, -1, 9, 16)
fun calculatePartial(first: Long, second: Long): Double {
var sum = 0L
val difference = first xor second
(0..60 step 4).onEach {
sum += precomputed[(difference.ushr(it) and 0xF).toInt()]
}
return sum.toDouble()
}
По памяти стало
2.160M против 1.600M — неприятно, но всё же лучше, чем начальные 4.200M.Посчитаем операции:
10M квадратных корней, сложений и делений (никуда не делись)270M XOR'ов4.320 сложений, сдвигов, логических И и извлечений из массива.Выглядит уже более интересно, но, всё равно, слишком много вычислений. К сожалению, похоже, что те 20% усилий, дающих 80% результата, мы тут уже потратили и пора подумать, где ещё можно выгадать. Первое, что приходит на ум, — вообще не доводить до расчёта, отфильтровывая заведомо неподходящие сигнатуры каким-нибудь легковесным фильтром.
Подход четвёртый, крупное сито
Если немного преобразовать формулу расчёта, то можно получить такое неравенство (чем меньше рассчитанная дистанция — тем лучше):
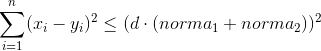
Т.е. теперь нам надо придумать, как на основании имеющейся у нас информации по количеству выставленных бит в
Long'ах вычислить минимальное возможное значение левой части неравенства. После чего просто отбрасывать все сигнатуры, ему не удовлетворяющие.Напомню, что xi может принимать значения от 0 до 4 (знак не важен, думаю, понятно почему). Учитывая, что каждое слагаемое возводится в квадрат, несложно вывести общую закономерность:
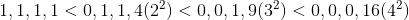
Конечная формула выглядит так (она нам не понадобится, но я довольно долго её выводил и было бы обидно просто забыть и никому не показать):
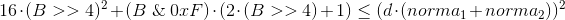
Где B — количество выставленных бит.
На самом то деле, в одном
Long'е всего 64 бита, читай 64 возможных результата. И они отлично рассчитываются заранее и складываются в массив, по аналогии с предыдущим разделом.Кроме того, совершенно необязательно просчитывать все 27
Long'ов — достаточно на очередном из них превысить порог и можно прерывать проверку и возвращать false. Такой же подход, кстати, можно использовать и при основном расчёте.fun getSimilar(signature: Signature) = collection
.asSequence() // Зачем нам лишняя промежуточная коллекция!?
.filter { estimate(it, signature) }
.filter { calculateDistance(it, signature) < d }
val estimateValues = arrayOf(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 19, 22, 25, 28, 31, 34, 37, 40, 43, 46, 49, 52, 55, 58, 61, 64, 69, 74, 79, 84, 89, 94, 99, 104, 109, 114, 119, 124, 129, 134, 139, 144, 151, 158, 165, 172, 179, 186, 193, 200, 207, 214, 221, 228, 235, 242, 249, 256)
fun estimate(first: Signature, second: Signature):Boolean{
var bitThreshold = Math.pow(d * (first.norma + second.norma), 2.0).toLong()
first.signature.forEachIndexed { index, value ->
bitThreshold -= estimateValues[java.lang.Long.bitCount(value xor second.signature[index])]
if (bitThreshold <= 0) return false
}
return true
}
Тут надо понимать, что эффективность данного фильтра (вплоть до отрицательной) катастрофически сильно зависит от выбранного порога и, чуть менее сильно, от входных данных. К счастью, для нужного нам порога
d=0.3 пройти фильтр удаётся довольно малому количеству объектов и вклад их обсчёта в общее время ответа настолько мизерный, что им можно пренебречь. А раз так, то можно ещё немножко сэкономить.Подход пятый, избавляемся от sequence
При работе с большими коллекциями,
sequence — это хорошая защита от крайне неприятного Out of memory. Однако если мы заведомо знаем, что на первом же фильтре коллекция уменьшится до вменяемых размеров, то гораздо более разумным выбором будет использовать обычный перебор в цикле с созданием промежуточной коллекции, потому как sequence — это не только модно и молодёжно, но ещё и итератор, у которого hasNext сотоварищи, которые совсем не бесплатны.fun getSimilar(signature: Signature) = collection
.filter { estimate(it, signature) }
.filter { calculateDistance(it, signature) < d }
Казалось бы, вот оно счастье, но захотелось «сделать красиво». Вот тут мы и подошли к обещанной поучительной истории.
Подход шестой, хотели как лучше
Мы же пишем на Kotlin, а тут какие-то инородные
java.lang.Long.bitCount! А ещё недавно в язык подвезли беззнаковые типы. В атаку!Сказано — сделано. Все
Long заменены на ULong, из исходников Java с корнем выдрана java.lang.Long.bitCount и переписана как функция расширения для ULongfun ULong.bitCount(): Int {
var i = this
i = i - (i.shr(1) and 0x5555555555555555uL)
i = (i and 0x3333333333333333uL) + (i.shr(2) and 0x3333333333333333uL)
i = i + i.shr(4) and 0x0f0f0f0f0f0f0f0fuL
i = i + i.shr(8)
i = i + i.shr(16)
i = i + i.shr(32)
return i.toInt() and 0x7f
}
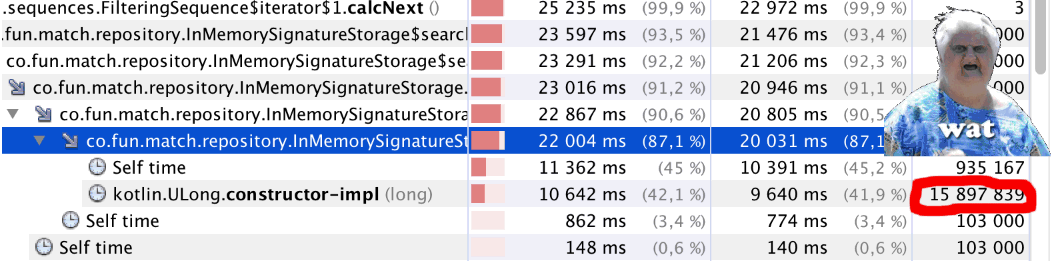
Запускаем и… Что-то не так. Код стал отрабатывать заметно медленнее. Запускаем профайлер и видим странное (см. заглавную иллюстрацию статьи): на чуть меньше миллиона вызовов
bitCount() почти 16 миллионов вызовов Kotlin.ULong.constructor-impl. WAT!?Загадка объясняется просто — достаточно посмотреть в код класса
ULongpublic inline class ULong @PublishedApi internal constructor(@PublishedApi internal val data: Long) : Comparable<ULong> {
@kotlin.internal.InlineOnly
public inline operator fun plus(other: ULong): ULong = ULong(this.data.plus(other.data))
@kotlin.internal.InlineOnly
public inline operator fun minus(other: ULong): ULong = ULong(this.data.minus(other.data))
@kotlin.internal.InlineOnly
public inline infix fun shl(bitCount: Int): ULong = ULong(data shl bitCount)
@kotlin.internal.InlineOnly
public inline operator fun inc(): ULong = ULong(data.inc())
и т.д.
}
Нет, я всё понимаю,
ULong сейчас experimental, но как так-то!?В общем и целом, признаём подход несостоявшимся, а жаль.
Ну, а всё-таки, может можно ещё что-то улучшить?
На самом деле, можно. Оригинальный код
java.lang.Long.bitCount — не самый оптимальный. Он даёт хороший результат в общем случае, но если мы заранее знаем на каких процессорах будет работать наше приложение, то можно подобрать более оптимальный способ — вот очень хорошая статья об этом на Хабре Обстоятельно о подсчёте единичных битов, крайне рекомендую к прочтению.Я использовал «Комбинированный метод»
fun Long.bitCount(): Int {
var n = this
n -= (n.shr(1)) and 0x5555555555555555L
n = ((n.shr(2)) and 0x3333333333333333L) + (n and 0x3333333333333333L)
n = ((((n.shr(4)) + n) and 0x0F0F0F0F0F0F0F0FL) * 0x0101010101010101).shr(56)
return n.toInt() and 0x7F
}
Считаем попугаев
Все замеры производились бессистемно, по ходу разработки на локальной машине и воспроизводятся по памяти, так что о какой-либо точности говорить сложно, но оценить приблизительный вклад каждого из подходов можно.
| Что делали | попугаи (секунды) |
|---|---|
| Подход первый, наивный | 25± |
| Подход второй, упаковываем | - |
| Подход третий, упаковываем заново с подвыподвертом | 11-14 |
| Подход четвёртый, крупное сито | 2-3 |
| Подход пятый, избавляемся от sequence | 1.8-2.2 |
| Подход шестой, хотели как лучше | 3-4 |
| «Комбинированный метод» подсчёта установленных битов | 1.5-1.7 |
Выводы
- Когда имеешь дело с обработкой большого количества данных, то стоит потратить время на предварительный анализ. Возможно, не все из этих данных надо обрабатывать.
- Если есть возможность использовать грубую, но дешёвую предварительную фильтрацию, то это может сильно помочь.
- Битовая магия — наше всё. Ну там, где она применима, конечно.
- Посмотреть исходники стандартных классов и функций иногда бывает очень полезно.
Спасибо за внимание! :)
И да, продолжение следует.
Комментарии (34)

APXEOLOG
16.05.2019 12:23+1Кстати, если кто-то предложит, как можно упростить вычисления при такой упаковке — получит большое спасибо и плюс в карму. Хоть и один, но зато от всей души :)
Честно скажу, лично не проверял и сам не использовал, но вроде как для битовых операций есть BitSet. Возможно он будет эффективнее
fun getSimilar(signature: Signature) = collection .filter { estimate(it, signature) } // Полный проход по коллекции .filter { calculateDistance(it, signature) < d } // Еще один полный проход
Мне кажется, если оставить только один фильтр, то вы избавитесь от лишнего прохода по коллекции
Вообще реализация фильтра основывается на ArrayList'е
public inline fun <T> Iterable<T>.filter(predicate: (T) -> Boolean): List<T> { return filterTo(ArrayList<T>(), predicate) }
Не забывайте, что ArrayList основывается на массиве и будет расширяться (т.е. выделяться новая память и производится копирование), что в вашем случае с 10 миллионами записей скорее всего приводит к сильному оверхеду. Как вариант — убрать все эти фильтры и оставить обычный
for (i in collection) {}который будет складывать результаты в заранее инициализированный ArrayList с примерно прикинутым размером
rjhdby Автор
16.05.2019 12:27Да, наверное стоило бы написать, что объединенные фильтры более выгодны (в реальном коде так и сделано). Тут для наглядности два оставлено.
Но на самом деле, как я отметил в статье, первый фильтр работает настолько хорошо, что на вход второго фильтра попадает уже довольно малая коллекция и вклад ее обработки в общее время ответа даже под микроскопом не видно.

rjhdby Автор
16.05.2019 12:48Ход мыслей верный, но в данном конкретном случае это не даст сколько-нибудь значимого прироста производительности, поскольку, как я отмечал, выходная коллекция первого фильтра крайне мала, а под капотом все эти красивые map'ы и filter'ы все одно преобразуются в for.
Как вариант — убрать все эти фильтры и оставить обычный for (i in collection) {}
:) Угадали, ловите плюсик

areht
16.05.2019 14:40так в итоге переход от byte к long что-то дал? Кажется, что упаковать по 4 бита можно и так и эдак, но код с byte будет проще.

rjhdby Автор
16.05.2019 14:42Будет в 8 раз больше XOR'ов и, соответственно, на предфильтрации больше шагов сравнения.

areht
16.05.2019 15:55> Кроме того, совершенно необязательно просчитывать все 27 Long'ов — достаточно на очередном из них превысить порог и можно прерывать проверку и возвращать false.
Не обязательно больше — может быть и меньше.
Да и в 8 раз больше XOR — это ещё не в 8 раз медленнее. На накиданном в лоб тесте (for(..) a xor b) разница 12%, если вычесть п.1 может ничего не остаться.
Но если нет — может в сторону SSE смотреть? Там можно не только XOR, но и биты считать.
rjhdby Автор
16.05.2019 17:30Хороший повод, чтобы потестить, займусь на досуге и отпишусь по результатам. :)
По SSE — тут двояко. Да, может дать хороший прирост, но это прибитие гвоздями к конкретной архитектуре. Если x64 VS x86 — еще более-менее прогнозируемо, то вот SSE… Поправьте, если не прав — не сильно углублялся в тему.

areht
16.05.2019 17:52А что, у вас есть планы переезда с x64?
ИМХО «переносимый код» бывает в библиотеках, а в вашей конкретной задаче вы же, наверное, знаете на чем это запускать будете ближайшие 5 лет.

a__v__k
16.05.2019 17:11А значения (x-y)^2 предвычисляете? всего-то 25 вариантов.

rjhdby Автор
16.05.2019 17:11Меньше.
val precomputed = arrayOf(0, 1, 1, 4, 1, -1, 4, 9, 1, -1, -1, -1, 4, -1, 9, 16)
a__v__k
16.05.2019 23:41А частоты выпадений для этих квадратов считать пробовали?
У вас ведь есть верхний предел — d^2 * (Nx + Ny)^2.
Можно посчитать частоты для (x-y) — массив счетчиков всего из 4 элементов (с отбросом знака и 0). А потом считать дистанцию, начиная с больших: 16 * Q[4] + 9 * Q[3] + 4 * Q[2] + 5 * Q[1]. В какой то момент дистанция перейдет за лимит и следующее умножение можно не проводить.
rjhdby Автор
16.05.2019 23:48Не совсем понял, что вы предлагаете.
Идея с предфильтрацией именно в том и состоит, чтобы максимально быстро/просто (с минимумом операций) отфильтровать гарантируя отсутствие ложно-негативных срабатываний.

vagola
16.05.2019 17:12По умолчанию реализация bitCount заменяется интринсиком

rjhdby Автор
16.05.2019 17:16Возможно, не буду спорить. Для 11 версии Java он помечен как кандидат в интрисики.
По факту собственная реализация оказалась быстрее, чем использованиеjava.lang.Long.bitCount. Буду благодарен, если расскажете, почему так получается.

masyaman
16.05.2019 19:16+1Можно сумму квадратов разности посчитать без циклов и ветвлений. Скорее всего будет быстрее, чем в приведенном примере.
В данном случае для значений [-2..2] я использовал по 4 бита на число: [0b0110, 0b0111, 0b0000, 0b0001, 0b0010].
Идея использовать побитовую магию для паралельного подсчета всех полубайтов лонга одновременно.
Код на джаве:
public static long sumSqDiff(long l1, long l2) { // l1 = l1 - l2 l1 |= 0x8888888888888888L; l1 -= l2; // l2 = negatives l2 = (l1 & 0x4444444444444444L) >>> 2; // l1 = abs(l1) l1 = (l1 ^ (l2 | (l2 << 1) | (l2 << 2))) + l2; // Calculate separate bits, prepare for multiplication long b0 = l1 & 0x1111111111111111L; // Bit 0b0001 b0 = b0 | (b0 << 1); // Bit 0b0001 -> 0b0011 long b1 = l1 & 0x2222222222222222L; // Bit 0b0010 b1 = b1 | (b1 >>> 1); // Bit 0b0010 -> 0b0011 long b2 = (l1 & 0x4444444444444444L) >>> 2; // Bit 0b0100 -> 0b0001 // l1 = l1 * l1 (low 2 bits only) l1 = ((l1 & b1) << 1) + (l1 & b0); // Calculate special case for value 4 0b0100 b2 = (b2 + (b2 >>> 4)) & 0x0F0F0F0F0F0F0F0FL; // Combine alltogether l1 = (l1 & 0x0F0F0F0F0F0F0F0FL) + ((l1 >>> 4) & 0x0F0F0F0F0F0F0F0FL) ; l1 += b2 << 4; l1 = (l1 + (l1 >>> 8)) & 0x00FF00FF00FF00FFL; l1 = (l1 + (l1 >>> 16)); l1 = (l1 + (l1 >>> 32)); return l1 & 0xFFFF; }
Надеюсь, у автора будет возможность проверить и написать результат.

rjhdby Автор
16.05.2019 19:31Не скрою — была у меня тайная цель увидеть комментарии такого рода ;)

masyaman
16.05.2019 23:14+1Не сомневаюсь, что ради этого и писалась статья :)
И, раз уж Вы так хотели уложить данные в 3 бита, то это тоже можно сделать. Правда, только 20 штук в long, а не 21, если без костылей просаживающих производительность.
Значения такие же как и в предыдущем примере, [0b110, 0b111, 0b000, 0b001, 0b010]. И все так же без веток и циклов:
public static final long BITS_001 = 0b001001001001001001001001001001001001001001001001001001001001001L; public static final long BITS_010 = BITS_001 << 1; public static final long BITS_100 = BITS_001 << 2; public static final long BITS_011 = BITS_010 | BITS_001; public static final long BITS_GROUP_0N =0b000111000111000111000111000111000111000111000111000111000111000L; public static final long BITS_GROUP_0 = 0b111000111000111000111000111000111000111000111000111000111000111L; public static final long BITS_GROUP_1 = 0b111000000111111000000111111000000111111000000111111000000111111L; public static final long BITS_GROUP_2 = 0b000111111111111000000000000111111111111000000000000111111111111L; public static long sumSqDiff(long l1, long l2) { // l2 = -l2, inverse L2 to use sum instead of substraction long l2Neg001 = (l2 | (l2 >>> 1) | (l2 >>> 2)) & BITS_001; long l2Neg111 = (l2Neg001 << 2) | (l2Neg001 << 1) | l2Neg001; l2 = (l2 ^ l2Neg111) + l2Neg001; // Calculate where substraction is needed (flip highest bit) long oneNeg100 = (l1 ^ l2) & BITS_100; // sum = l1 + l2 long sum = ((l1 & BITS_011) + (l2 & BITS_011)) ^ oneNeg100; // sum = abs(sum) long sumNeg001 = (sum & BITS_100) >>> 2; long sumNeg111 = (sumNeg001 << 2) | (sumNeg001 << 1) | sumNeg001; sum = (sum ^ sumNeg111) + sumNeg001; // Calculate separate bits, prepare for multiplication long b0 = sum & BITS_001; // Bit 0b001 b0 = b0 | (b0 << 1); // Bit 0b001 -> 0b011 long b1 = sum & BITS_010; // Bit 0b010 b1 = b1 | (b1 >>> 1); // Bit 0b010 -> 0b011 long b2 = (sum & BITS_100) >>> 2; // Bit 0b100 -> 0b001 // mul011 = l1 * l1 (low 2 bits only) long sumPart1 = sum & BITS_GROUP_0; long sumPart2 = sum & BITS_GROUP_0N; long res = ((sumPart1 & b1) << 1) + (sumPart1 & b0) + ((((sumPart2 & b1) << 1) + (sumPart2 & b0)) >>> 3); // Calculate special case for value 4 = 0b100 b2 = (b2 + (b2 >>> 3)) & BITS_GROUP_0; b2 = (b2 + (b2 >>> 6)) & BITS_GROUP_1; // Combine alltogether res = (res + (res >>> 6)) & BITS_GROUP_1; res += b2 << 4; res = (res + (res >>> 12)) & BITS_GROUP_2; res = (res + (res >>> 24)); res = (res + (res >>> 48)); return res & 0xFFF; }
Не знаю как будет по скорости. Наверно можно еще что-то соптимизировать, но я пока пас. Скорее всего примерно так же, как и в предыдущем примере. Но памяти меньше.
Буду ждать от Вас результатов тестов.

rjhdby Автор
17.05.2019 01:09То на то вышло: 1.5-1.7, но надо посмотреть, возможно получится где-нибудь еще сэкономить. Ну и пару нюансов еще проверить.
Но вообще зачет — сам люблю битики посмещать, но до вас еще очень далеко. Супер! :)
masyaman
17.05.2019 09:53Странно, что нет повышения производительности. Возможно, что узкое место где-то не здесь. Попробуйте сравнить два (или три) решения без применения предварительного фильтра.
Я еще немного подчистил код для трехбитной реализации. Улучшение производительности в рамках погрешности, хотя вроде и есть.
public static long sumSqDiff(long l1, long l2) { // l2 = -l2, inverse L2 to use sum instead of substraction long l2NotZero001 = (l2 | (l2 >>> 1)) & BITS_001; long l2Neg111 = (l2NotZero001 << 2) | (l2NotZero001 << 1) | l2NotZero001; l2 = (l2 ^ l2Neg111) + l2NotZero001; // Calculate where only one negative value is present (flip highest bit) long oneNeg100 = (l1 ^ l2) & BITS_100; // sum = l1 + l2 long sum = ((l1 & BITS_011) + (l2 & BITS_011)) ^ oneNeg100; // sum = abs(sum) long sumNeg100 = sum & BITS_100; long sumNeg001 = sumNeg100 >>> 2; long sumNeg111 = sumNeg100 | (sumNeg001 << 1) | sumNeg001; sum = (sum ^ sumNeg111) + sumNeg001; // Calculate separate bits, prepare for multiplication long b0 = sum & BITS_001; // Bit 0b001 b0 = b0 | (b0 << 1); // Bit 0b001 -> 0b011 long b1 = sum & BITS_010; // Bit 0b010 b1 = b1 | (b1 >>> 1); // Bit 0b010 -> 0b011 long b2 = (sum & BITS_100) >>> 2; // Bit 0b100 -> 0b001 // mul011 = l1 * l1 (low 2 bits only) long sumPart1 = sum & BITS_GROUP_0; long sumPart2 = sum & BITS_GROUP_0N; long res = ((sumPart1 & b1) << 1) + (sumPart1 & b0) + ((((sumPart2 & b1) << 1) + (sumPart2 & b0)) >>> 3); // Calculate special case for value 4 = 0b100 b2 = (b2 + (b2 >>> 3)) & BITS_GROUP_0; // Combine alltogether res += b2 << 4; res = (res & BITS_GROUP_1) + ((res >>> 6) & BITS_GROUP_1); res = (res + (res >>> 12)); res = (res + (res >>> 24)); res = (res + (res >>> 48)); return res & 0xFFF; }
rjhdby Автор
18.05.2019 10:18Странно, что нет повышения производительности. Возможно, что узкое место где-то не здесь. Попробуйте сравнить два (или три) решения без применения предварительного фильтра.
На всякий случай поясню, чтобы не оказалось, что о разном говорим. Фильтр по количеству бит крайне эффективен и, из-за этого, является узким местом. Грубо говоря, 99% времени тратится именно на него. Соответственно, отдельно улучшать окончательный расчет смысла мало — надо что-то делать с фильтром. И вот тут ваш вариант оказывается эдакой "серебряной пулей", которая может заменить фильтр и, как приятный бонус, сразу рассчитать результат.
Почему производительность осталась той же? (с равными шансами она могла как вырости, так и снизиться кстати)
Моя реализация фильтра хоть и режет исходя из самого негативного сценария (обрабатывается больше Long'ов из каждой сигнатуры), но крайне легковесна. Ваша реализация работает с реальными данными, cutoff происходит на более ранних стадиях, но вес каждой итерации больше.
Как-то так. :)
PS А не написать ли вам статью про битовую магию? Разные подходы, приемы, занятные алгоритмы. Я бы с удовольствием почитал.

masyaman
18.05.2019 12:41Я понял.
Переписал Ваш код на джаву и проверил производительность с помощью JMH.
Реализация с циклом примерно в 2 раза медленнее моей 4хбитной реализации. Трехбитная реализация была медленнее, но у меня уже есть решение с оптимизацией. Новое решение даже чуть обгоняет четырехбитное (правда, не понимаю почему), но в нем на 25% больше данных, так что в итоге должно быть быстрее и с меньшим потреблением памяти. Грубый фильтр примерно в 6 раз быстрее моей самой быстрой реализации (но это в пересчете на один long а не на количество реальных данных в нем).
Вот результаты тестов:
Benchmark Mode Cnt Score Error Units Jmh.bits3new thrpt 5 171994.412 ± 925.414 ops/s Jmh.bits3old thrpt 5 117730.344 ± 10353.670 ops/s Jmh.bits4 thrpt 5 163883.382 ± 2206.193 ops/s Jmh.ref thrpt 5 77606.405 ± 968.108 ops/s Jmh.refEstimate thrpt 5 1027086.177 ± 23775.351 ops/s
Ну и оптимизированый код:
public static final long BITS_001 = 0b001001001001001001001001001001001001001001001001001001001001001L; public static final long BITS_010 = BITS_001 << 1; public static final long BITS_100 = BITS_001 << 2; public static final long BITS_011 = BITS_010 | BITS_001; public static final long BITS_GROUP_0N =0b000111000111000111000111000111000111000111000111000111000111000L; public static final long BITS_GROUP_0 = 0b111000111000111000111000111000111000111000111000111000111000111L; public static final long BITS_GROUP_1 = 0b111000000111111000000111111000000111111000000111111000000111111L; public static final long BITS_MUL = 0b000000000000001000000000001000000000001000000000001000000000001L; public static long sumSqDiff(long l1, long l2) { // Calculate same sign places long sameSign100 = (~(l1 ^ l2)) & BITS_100; // sum = l1 - l2 long sum = ((l1 | BITS_100) - (l2 & BITS_011)) ^ sameSign100; // sum = abs(sum) long sumNeg001 = (sum & BITS_100) >>> 2; sum = (sum ^ (sumNeg001 * 7)) + sumNeg001; // Calculate separate bits, prepare for multiplication long b0 = (sum & BITS_001) * 3; // Bit 0b001 -> 0b011 long b1 = (sum & BITS_010) * 3; // Bit 0b010 -> 0b110 // mul011 = l1 * l1 (low 2 bits only) long sumPart1 = sum & BITS_GROUP_0; long sumPart2 = sum & BITS_GROUP_0N; long res = ((sumPart1 << 1) & b1) + (sumPart1 & b0) + ((((sumPart2 << 1) & b1) + (sumPart2 & b0)) >>> 3); // Calculate special case for value 4 = 0b100 long b2 = (sum & BITS_100) << 2; res += (b2 + (b2 >>> 3)) & BITS_GROUP_0N; // Combine alltogether res = (res & BITS_GROUP_1) + ((res >>> 6) & BITS_GROUP_1); res = (res * BITS_MUL) >>> 48; return res & 0xFFF; }
Статью писать я вряд ли буду, я не так много могу рассказать по этому поводу. Но могу порекомендовать отличную книгу по теме, называется
Hacker's Delightили в русском переводеАлгоритмические трюки для программистов.

masyaman
19.05.2019 13:35Ваша задача не отпускает :)
Обнаружил, что джава считает Long.bitCount очень быстро, по крайней мере на моей системе. Скорее всего задействует SSE инструкции или типа того.
А в связи с этим открываются новые возможности по оптимизации:
public static long sumSqDiff(long l1, long l2) { long sameSign100 = (~(l1 ^ l2)) & BITS_100; // sum = l1 - l2 long sum = ((l1 | BITS_100) - (l2 & BITS_011)) ^ sameSign100; // correct estimate: add cases for values +/-3 return Long.bitCount(((sum ^ (sum << 1)) & BITS_100) & (sum << 2)) * 8 + estimate(l1, l2); } public static long estimate(long l1, long l2) { long xor = l1 ^ l2; long ones = xor & BITS_001; long res = Long.bitCount(ones); xor &= ~(ones * 7); long twos = xor & BITS_010; res += Long.bitCount(twos) * 4; xor &= ~(twos * 3); res += Long.bitCount(xor) * 16; return res; }
Это пока самый быстрый код, который я смог получить на своей системе. Не факт что на Вашей системе будет так же.
Методestimateмедленнее, чем у Вас, но более точный. Из плюсов, можно грубо посчитать грубую оценку, а потом при необходимости досчитать. Хотя в Вашем случае выигрыш от такого подхода будет совсем небольшой.
rjhdby Автор
19.05.2019 19:40Тут все упирается в баланс "количество операций"*"вес операции" и, на самом, деле, оптимальность того или иного кода будет сильно зависит от входных данных. Если, допустим разница на каждом лонге (с моим методом кодирования, для простоты) будет
0001 0001 0001 0001, то быстрее работать будет мой способ оценки, а если0000 0000 0000 1111, то ваш. Промежуточные варианты — тут надо оценивать, скорее всего можно высчитать порог1,1,1,1->0,1,1,2->0,0,1,3->0,0,0,4, на котором перадается первенство.

rjhdby Автор
19.05.2019 20:01Кстати, не думали на тему скомбинировать битовую магию с массивом предрасчитанных значений? Например (чисто полет фантазии) всего 256 комбинаций выставленных первых бит в каждом байте для Long'а.

masyaman
19.05.2019 21:20Идея интересная. У меня получился результат примерно на уровне моего последнего решения. Но в тут таки можно использовать память по полной и поместить 21 значения в long.
Из минусов такого подхода — надо подбирать размер массива для конкретного железа. У меня получился лучший результат при 2^12 интов, по 4 трехбитных слова. При использовании 2^9 или 2^15 производительность становится хуже. Так же она становится хуже при использовании массива байтов вместо инта. На Вашем железе может быть по-другому.
Алгоритм простой, сначала посчитать разность (см. предыдуйие код, 2 первые строчки), а потом посуммировать из массива. Если захотите проверить, то разберетесь как это сделать :)
Ну и я бы рекомендовал все-таки проверить мои 2 последних решения на Ваших данных и Вашем железе. Даже если по скорости он окажется таким же, то по памяти будет выигрыш. И мне тоже хотелось бы узнать результат :)

khayrov
16.05.2019 20:11Эта статья про константу, а продолжение, случаем, не о поиске быстрее O(N) планируется? Поиск соседей в многомерном пространстве с евклидовой метрикой вроде сравнительно хорошо проработанная тема: locality-sensitive hashing и т.д.

rjhdby Автор
17.05.2019 00:29В планах есть, но пока в неопределенных. Следующая будет обзорная про алгоритм Голдберга поиска схожих изображений с некоторыми его доработками (на самом то деле писалось именно она, но в процессе пришло понимание, что вот этот кусок про нюансы конкретной реализации будет там совсем не к месту)

igormich88
17.05.2019 03:08Я кстати так и не понял зачем происходит вызов constructor-impl для inline классов. Так как этот конструктор для всех inline классов компилируется в статический метод примерно такого вида, а из-за запрета на блок init в inline классе мы при всём желании не сможем его расширить (ниже декомпилированный метод)
Почему его не инлайнят непонятно.@NotNull public static ActualClass constructor-impl(@NotNull ActualClass s) { Intrinsics.checkParameterIsNotNull(s, "s"); return s; }
Для примитивных типов метод выглядит еще проще (и бесполезней).
Может быть при выводе из экспериментальной версии исправят эту проблему.public static long constructor-impl(long data) { return data; }


koldyr
Может быть я не правильно понял, но, считайте не d, а d в квадрате. Нормы и квадраты норм x и y можно предвычислить и хранить рядом с ними. И того, после преобразований, из тяжёлого останется только (x,y).
rjhdby Автор
Да, естественно предвычисляем все, что только возможно. Нормы вот они — вторым параметром конструктора.
koldyr
Зачем вам плавающие с двойной точностью, если исходные данные целые по два бита? Мне кажется это сильный оверпауэр. Может быть достаточно fixpoint с четырьмя знаками после точки?
rjhdby Автор
Хм… Стоит попробовать, спасибо.
koldyr
Ещё раз посмотрел текст статьи и повторюсь. Не считайте d считайте d^2. Тогда в числителе будет сумма квадратов норм минус удвоенное скалярное произведение, а в знаменателе — сумма квадратов норм плюс удвоенное произведение норм. Если вы протягиваете элемент по коллекции, то можно умножения на 2 сделать один раз за прогон. Корень извлекать не надо, сравнивайте с квадратом порогового значения.
rjhdby Автор
Могу лишь повторить
Эта идея лежит на поверхности и я решил не акцентировать на ней внимания в пользу наглядности и простоты кода. (вы же не думаете, что в реальном проекте вот ровно вот это все написано и именно таким образом?)