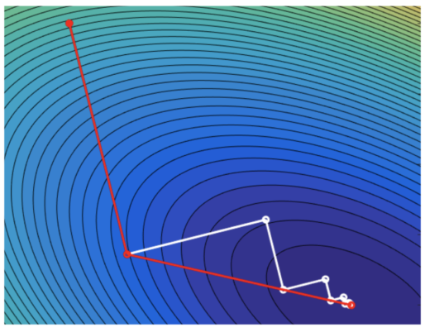
Я работаю в американской компании, разрабатывающей софт для химической и нефтегазовой промышленности. Одной из наиболее востребованных тем в этой области является оптимизация чего-либо при заданных параметрах производства. Например, минимизация расходов на выработку какого-нибудь газа, максимизация прибыли при реализации топлива, максимизация давления в какой-нибудь трубе при вариабельных термодинамических параметрах на другой части проектируемого завода и заданных ограничениях и т.д. Я занимался реализацией методов оптимизации для подобных задач и, думаю, накопил ощутимый опыт в этой области. С этого поста хотел бы начать серию обзоров известных методов оптимизации.
Введение
Оптимизация — это процесс нахождения точки экстремального значения некоторой заданной целевой функции . Это один из крупнейших краеугольных камней прикладной математики, физики, инженерии, экономики, промышленности. Область её применений необъятна и может распространяться от минимизации физических величин на микро- и макроуровнях до максимизации прибыли или эффективности логистических цепочек. Машинное обучение также заострено на оптимизации: всевозможные регрессии и нейроные сети пытаются минимизировать ошибку между предсказанием и реальными данными.
Экстремум может быть как минимумом, так и максимумом, но обычно принято изучать любую оптимизацию исключительно как поиск минимума, поскольку любая максимизация эквивалентна минимизации из-за возможности поменять знак перед целевой функцией: . Следовательно, в любом месте ниже под оптимизацией мы будем понимать именно минимизацию.
Некоторые посты по оптимизации на Хабре от других авторов:
Обзор градиентных методов в задачах математической оптимизации
Обзор основных методов математической оптимизации для задач с ограничениями
Метод BFGS или один из самых эффективных методов оптимизации. Пример реализации на Python
Квазиньютоновские методы, или когда вторых производных для Атоса слишком много
Метод оптимизации Trust-Region DOGLEG. Пример реализации на Python
Раздел численных методов, изучающий оптимизацию общих нелинейных функций, называется нелинейным программированием, или NLP (конечно, сейчас на слуху у всех другое NLP — Natural Language Processing, но это не тот случай).
Кто хочет сразу перейти к сердцевине — можно перескочить к главе «Характеристики методов».
Типы оптимизаций
Безусловная vs условная
Следующая оптимизация
является безусловной и имеет решение , в то время как добавление неравенства как показано
делает оптимизацию условной и порождает решение .
В механике равенства соответствуют двусторонним ограничениям. Это может быть, например, условие, при котором материальная точка никогда не покидает определённую поверхность, пока её потенциальная энергия сводится к минимуму. Односторонние ограничения, с другой стороны, соответствуют неравенствам и распространены в негладкой механике, например: столкновения, непроникновение поверхностей сквозь друг друга, трение и т. д. Такие системы рассматриваются с помощью множителей Лагранжа, представляющих силы реакции со стороны поверхностей.
В данном посте мы будем рассматривать безусловную оптимизацию, а к условной, может быть, перейдём в другой раз.
Локальная vs глобальная
Определение. Точка является локальным минимизатором (точкой локального минимума) целевой функции , если существует окрестность точки такая, что для любой точки в . Локальный минимизатор называется строгим, если указанное выше неравенство строгое для всех из и .
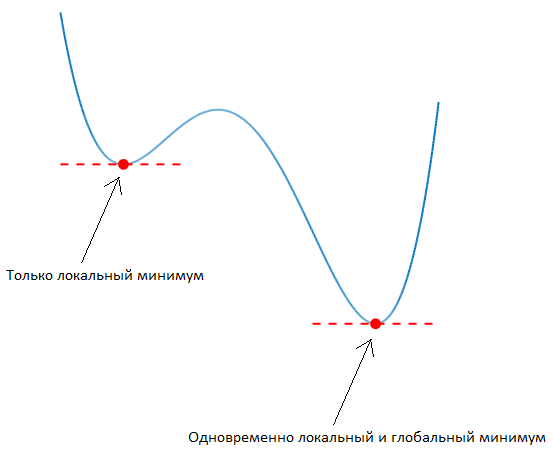
Мы будем здесь рассматривать только локальную оптимизацию.
Гладкая vs негладкая
В другом случае смысл «Гладкая vs негладкая» состоит в том, что идёт разделение между самими функциями: какие-то гладкие, а какие-то только непрерывные или даже разрывные. Понятно, что считать производные для последних не всегда будет корректным, или её расчёт крайне неточен. Например, метод Нелдера-Мида не требует какой-то информации о гладкости функции выше непрерывности для своей работы и вполне себе подходит для работы с функциями класса (само по себе это, конечно, не значит, что на более гладких функциях он не будет работать надёжнее).
Во втором разделении я не шибко разбираюсь и подозреваю, что набор методов эксклюзивно для негладких функции более худосочен, чем для гладких функций. В любом случае, эти два разделения условны и часто не имеют чёткой границы.
Ниже мы рассмотрим методы, которые нацелены как минимум на непрерывно-дифференцируемые функции, т.е. из класса . Последнее условие требуется, чтобы иметь возможность положиться на обширную доступную теорию гладких функций, а также использовать как минимум градиент функции для ускорения процесса поиска. Как известно, если является локальным минимизатором, то . Обратное, к сожалению, неверно.
Трудоёмкость целевой функции
Дополнительные трудности могут возникать в задачах, в которых целевая функции вычислется неточно, а с некоторым шумом, вносящим неопределённость.
Алгоритмы, которые мы будем рассматривать ниже, не принимают во внимание возможную трудоёмкость целевой функции и предполагают, что мы можем её вычислять без ограничений столько раз, сколько нам нужно. Нам важна оптимальность самих алгоритмов оптимизации.
Разделений ещё больше
Поскольку оптимизация является активно развивающейся и актуальной областью, она содержит слишком много — безумного много — тематических подобластей и вариаций. Задачи, требующие оптимизации, и методы для них растут как грибы после дождя на протяжении многих лет.
Например, есть огромная подобласть Mixed-Integer Programming, в которой рассматриваются дискретные сценарии. Есть недетерминированная (хаотическая) оптимизация, использующая вероятностные подходы в своей работе. Есть робастная оптимизация, в которую заложены параметры, не являющиеся переменными. Есть оптимизация динамических систем, в которых присутствует эволюция во времени. Есть всевозможные мета-эвристические методы: метод имитируемого отжига (simulated annealing), генетические алгоритмы, методы эволюции роя. Есть оптимизация неопределённой логики (fuzzy logic optimization).
Есть бог знает что! Я знаю лишь какую-то часть из представленного, и обо всём точно не расскажу никогда.
Даже по гладким методам я не смогу представить их все с достаточно глубоким анализом по каждому из них из-за нехватки времени и ресурсов. Я, однако, сделаю все возможное, чтобы передать основные идеи читателю.
Наши реалии
Численная минимизация непрерывной невыпуклой функции не дает гарантии, что полученное решение действительно является точкой локального минимума. Критерий останова метода проверяет магнитуду градиента функции и прерывает алгоритм в случае, если эта магнитуда ниже некоторого малого значения . Теоретически доказанные результаты сходимости с таким критерием существуют для многих методов, но его можно обмануть, заменив минимизатор произвольной стационарной точкой, что приведёт к невозможности предоставить истинное решение.
Например, для функции начальное приближение уже будет ответом, ввиду того, что , но ответ этот фейковый, т.к. представляет собой локальный максимум, в то время как реальная точка минимума — это любая из .
Что в этом случае делать? Ничего. Скрестить пальцы и надеяться на лучшее.
По этой причине, наши методы отвечают только за определение местоположения стационарной точки, хоть и будучи подкреплены сильной теоретической базой, подогревающей наши надежды на то, что такая точка всё-таки является локальным минимизатором для большинства функций, с которыми мы сталкиваемся в реальных задачах.
Есть и другая оговорка. Некоторые функции, которые формально являются гладкими, на самом деле могут быть слишком нерегулярными, чтобы методы надёжно производили минимизацию. И это ожидаемо, когда дискретный подход используется на задачах континуума (в отличие, например, от фундаментально дискретных задач, связанных с разреженными матрицами, графами и т. д.).
Как пример, картинка ниже демонстрирует гипотетический сценарий, когда математически реальный минимум может быть скрыт от глаз за счёт неплотности чисел с плавающей точкой во множестве . Чёрные точки показывают возможные итерации метода.
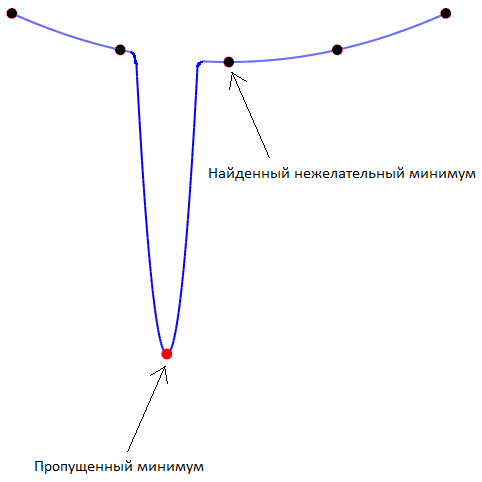
Что в этом случае делать? Ничего. Скрестить пальцы и надеяться на лучшее.
Характеристики методов
Рассматриваемые ниже методы минимизации можно разделить по множеству актуальных характеристик. В этом посте нам могут быть интересны следующие:
- Глобальная сходимость.
- Скорость локальной сходимости.
- Размеры задачи, на которую они нацелены.
- Требуется ли хранить в памяти матрицы или нет.
- Требуется ли матрица Гессе или нет.
- Требуется ли масштабирование или нет.
Первые два пункта являются теоретическими, другие же более приземлены и непосредственно относятся к практической реализации. Пройдёмся по каждому из пунктов.
Говорят, что метод имеет свойство глобальной сходимости, если его итерации сходятся к локальному минимизатору независимо от начального положения (не путать с поиском глобального минимизатора!). Скорость локальной сходимости показывает, насколько быстро метод «настигает» минимизатор, когда он уже достаточно близко подошёл к нему. Удивительно, но эти две характеристики метода, будучи обе очень желательными в реальных вычислениях, могут конфликтовать между собой в многих методах оптимизации. Так называемые гибридные методы умело используют оба этих преимущества.
Размер задачи сужает выбор до тех методов, которые мы можем себе позволить. Для крупных задач интенсивное использование памяти может быть недопустимым, и для таких задач используют методы, возникшие из таких ограничений и основанные на экономном потреблении памяти. Параллельно рассматривается вопрос, нужны ли нам плотные матрицы в итерационных вычислениях или нет, поскольку объём памяти для матриц растёт квадратично с увеличением размера задачи.
Матрица Гессе это такая матрица, у которой -компонента равна . Эта матрица использует информацию о второй производной функции (кривизне) и, при правильном использовании, обеспечивает более быструю сходимость за счёт лучшего определения направления шага. Получить такую матрицу для решателя может быть проблематично, в зависимости от типа и условий задачи. Это особенно верно для крупномасштабных задач или сценариев, использующих опосредованный расчёт функции (когда функция не предоставляется нам удобной аналитической формулой). Из матана известно, что если в стационарной точке матрица Гессе положительно определена (SPD), то эта точка является строгим локальным минимизатором. На практике это условие не проверяется даже при наличии матрицы Гессе, ибо слишком затратно проверять знаковую определённость матрицы.
Наконец, для некоторых методов может потребоваться масштабирование (скейлинг). Эффективность метода может зависеть от того, как именно поставлена задача. Задача плохо масштабируется, если изменения для в определённом направлении приводят к гораздо большим изменениям в значении , чем в другом направлении. Простым примером является , которая чувствительна к изменениям , но не чувствительна к изменениям . Некоторые методы, применяемые к таким задачам, могут страдать от медленной сходимости. Чтобы ускорить сходимость в этом примере, рекомендуется выполнить масштабирование, изменив переменные на новую пару . Некоторые методы нечувствительны к масштабированию, поэтому они предпочтительнее в практических ситуациях. Увы, на практике о целевой функции мало что бывает известно, и никто нам не предоставляет масштабирующих коэффициентов.
Ну а теперь, имея представления об основных характеристиках методов оптимизации, мы наконец можем перечислить сами методы — наиболее известные из них. На самом высоком уровне все методы гладкой локальной безусловной оптимизации можно разделить на два больших класса: методы линейного поиска (или методы линий) и методы доверительной области. В этом посте нас будет интересовать только первый класс.
Методы линий
Основная суть методов линий заключается в том, что на каждой итерации они выполняют поиск одномерного минимизатора в заданном направлении, которое они вычислили ранее. Грубо говоря, их алгоритмы имеют следующий паттерн:
k := 0
while
- рассчитать направление
- найти такое , что функция минимизируется
- k := k + 1
Методы этого класса между собой различаются, как правило, тем, как они генерируют направление на шаге 1, и — реже — тем, как они реализуют шаг 2. Тем не менее, что объединяет эти методы при выполнении шага 1 — это то, что все они пытаются рассчитать так называемое направление спуска . Это такое направление, которое обеспечивает мгновенное уменьшение целевой функции, если движется вдоль него. Можно провести аналогию из реальной жизни: человек, идущий по холму, всегда знает, в каком направлении в данном месте идет подъём, а в каком спуск, и выбирает то, которое ему нужно.
Формально, направление спуска определяется так, что выполняется неравенство , означающее, что угол между градиентом функции, всегда указывающим в сторону роста, и направлением больше 90 градусов. Указание направления спуска гарантирует корректность одномерной подзадачи минимизации на шаге 2, если предполагать, конечно, что целевая функция начинает расти, когда становится достаточно большим. А это, в свою очередь, гарантируется ограниченностью функции снизу. Не будем же мы искать минимум у неограниченной снизу функции. :)
Шаг 2 почти никогда не вычисляется точно, несмотря на одномерность задачи. Дело в том, что для этого может потребоваться дорогостоящая оценка матрицы Гессе целевой функции. По этой причине эта подзадача заменяется неточным аналогом, запрашивающим такую позицию , которая обеспечивает в каком-то смысле «хорошее» уменьшение функции. Существует несколько типов условий, которые используются как критерии решения этой неточной задачи, и все они формализованы как те или иные неравенства. Наиболее известны следующие:
- Условие Армиджо (или Армихо, фиг знает), или условие достаточного убывания
- Условия Вульфа двух типов: стандартное и сильное
- Условия Голдштайна
Первое условие заботится о том, чтобы в направлении поиска достигалось достаточно существенное уменьшение целевой функции. Несоблюдение этого условия может привести к стагнации процесса редукции (например, уменьшение может происходить на положительное значение, уменьшающееся от итерации к итерации) во всём алгоритме минимизации. Условия Вульфа в оригинале состоят из двух, первое из которых — само условие Армиджо, а второе называется условием кривизны. Последнее в свою очередь делится на стандартное и сильное условия кривизны и означает, что число достаточно велико, чтобы обеспечивать разумный прогресс в пространстве переменных (простым языком: мы хотим, чтобы сдвигался достаточно далеко, а не топтался на месте).
Сильное условие Вульфа, как очевидно из названия, «усиливает» условие кривизны таким образом, что помещается в окрестность точного минимизатора. Наконец, условия Голдштайна имеют примерно ту же цель, что и условия Вульфа, хотя они могут исключить фактический одномерный минимизатор из области поиска по чистой случайности. Условия представлены в таблице ниже, где мы используем обозначения , , .
| Название | Армиджо | Вульф: стандартное | Вульф: сильное | Голдштайн |
|---|---|---|---|---|
| Неравенства |
Ниже изображены четыре условия из таблицы, в указанном порядке: Армиджо, стандартный Вульф, сильный Вульф, Голдштайн. График относится к во всех случаях. Его красные части соответствуют тем значениям , которые удовлетворяют соответствующему условию. обозначает точный одномерный минимизатор: .
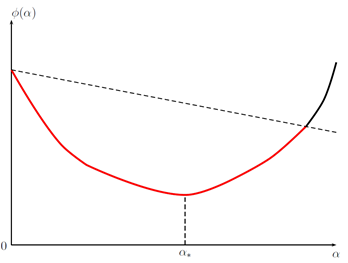
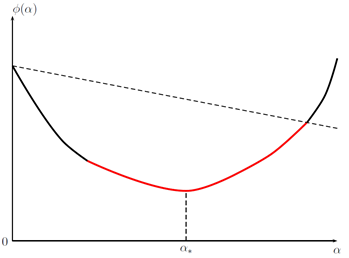
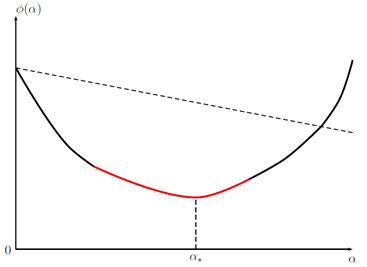
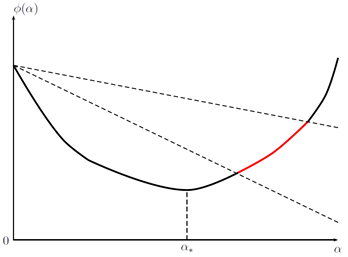
Кстати, в машинном обучении коэффициент называют скоростью обучения — learning rate (в самой же оптимизации названия не помню, может что-то вроде «шаг поиска»?).
Условия Вульфа обладают некоторыми доказанными свойствами, связанными с глобальной сходимостью. Приведём ниже очень важную теорему о глобальной сходимости методов линий.
Теорема. Пусть целевая функция ограничена снизу и везде дифференцируема, причём её градиент непрерывен по Липшицу: существует константа такая, что для любой пары . Пусть есть направление спуска, а удовлетворяет стандратному условию Вульфа для всех . Обозначим положительный косинус угла между и как . Тогда ряд сходится.
Непрерывность по Липшицу не является слишком ограничивающим условием. Напомним из математического анализа, что это условие гладкости находится между равномерной непрерывностью и дифференцируемостью. Другими словами, если дважды дифференцируема, то липшицева непрерывность градиента гарантируется.
Хорошая новость в том, что сходимость ряда означает сходимость его последовательности к нулю, что также известно из математического анализа. Иными словами, заключаем, что . Плохая же новость в том, что это само по себе не гарантирует сходимости к стационарной точке из-за присутствия косинуса рядом. Если можно показать, что последовательность косинусов ограничена снизу положительной константой, то сходимость к стационарной точке подразумевается. Но если выяснится, что , т.е. что направление становится всё меньше и меньше направлением спуска из-за стремления к ортогональности градиенту, то факта стремления к стационарной точке может и не быть. Этот фундаментальный недостаток алгоритма может быть одной из основных причин, по которым методы доверительной области имеют такое же право на существование, как и методы линий.
Одномерная минимизация
Второй шаг в алгоритме методов линий выглядит так:
Как можно добиться приближённого решения для этой задачи одномерной минимизации?
Более конкретно, нас интересует удовлетворение того или иного условия Вульфа.
Есть относительно простой алогоритм для этих целей. Допустим, нам требуется сильное условие Вульфа. Начиная с некоторого начального приближения , мы каким-нибудь образом шагаем либо вперёд (т.е. последовательность возрастает), либо назад (т.е. убывает, по-английски это называется backtracking). А по ходу шагания, мы проверяем следующие условия в представленном порядке, при учёте невыполнения предыдущих:
- Неравенство Армиджо не выполнено или
- Условие Вульфа выполнено
Если выполнено второе условие, то цель достигнута. Если выполнено первое или третье, то мы проваливаемся в следующий алгоритм по названием «Зум», позволяющий локализовать нужную нам точку для выполнения условия Вульфа. Это напоминает работу под увеличительным стеклом, отсюда и название.
Если выполнено первое условие, то мы на вход «Зуму» подаём два параметра . Если же третье, то подаём их же, но в другом порядке.

Вот так графически могут выглядеть итерации алгоритма «Зум», где красный участок соответствует выполнению сильного условия Вульфа:
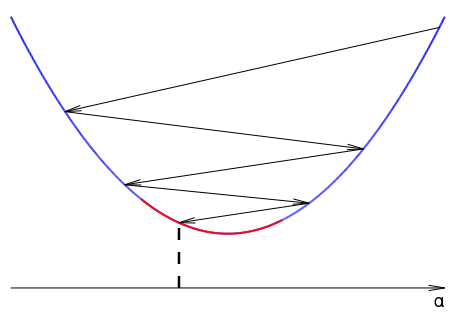
Давайте теперь посмотрим на самые известные алгоритмы безусловной оптимизации метода линий.
Метод наискорейшего спуска
Он же метод градиентного спуска. В алгоритме 1, шаг 1 цикла просто нам выдаёт . Да, вот так просто. Для этого случая просто всегда имеем , и глобальная сходимость по теореме выше нам гарантирована. Скорость сходимости линейна, и метод требует масштабирования. Например, для целевой функции с начальным положением наискорейший спуск может потребовать десятки итераций, чтобы сойтись к минимизатору , в то время как при масштабировании с коэффициентами , которые применяются к градиенту, уже одной итерации может быть достаточно, поскольку такое направление указывает непосредственно на начало координат. Метод не требует никакого матричного хранения в памяти.
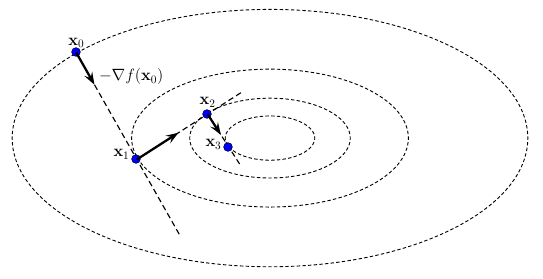
На рисунке выше показаны первые три итерации, выполненные методом наискорейшего спуска в сторону минимизатора на возможной выпуклой функции, например, выпуклой квадратичной функции. Здесь продемонстированы точные одномерные минимизаторы вдоль направлений , что эквивалентно тому, что вектор антиградиента касателен линии уровня функции, на которой лежит следующее приближение . Это также эквивалентно тому, что два последовательных градиента ортогональны друг другу. На практике, т.е. при неточной одномерной минимизации вдоль направления, такое случается крайне редко.
На рисунке ниже показано, как ведет себя наискорейший спуск при масштабировании с идеально подходящими положительными коэффициентами, содержащимися в диагональной матрице для той же целевой функции, что изображена на предыдущем рисунке.
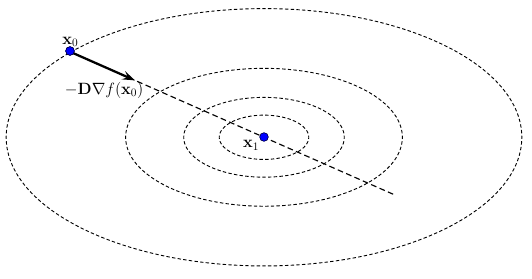
Антиградиент сразу указывает на точный минимизатор! Обратите внимание, что в случае неточного поиска вдоль линий, например, с использованием условий Вульфа, даже этот сценарий может потребовать немного больше одной итерации, чтобы сойтись. Все направления в этом случае будут параллельны друг другу.
Метод наискорейшего спуска является бесспорным «королём» глобальной сходимости. Это значит, что он сможет, во что бы то ни стало, достичь ямы, в которой располагается искомый минимизатор. Однако метод страдает от первого порядка сходимости, не позволяющего ему быстро «схватить» этот минимизатор. Он будет топтаться в его окрестности, неуверенно приближаясь к нему. Именно по этой причине я называю этот метод «дальнозорким».
Тем не менее, наискорейший спуск известен и используется всеми, от студентов, сдающих зачёты, до питоновских инженеров по машинному обучению. Причина в его теоретической простоте и одновременно в дешевизне реализации. Производные второго порядка целевой функции, как правило, недоступны при фиттинге нейронными сетями, поэтому дорогостоящий метод Ньютона (популярный больше среди академических исследователей) в таких ситуациях даёт дорогу наискорейшему спуску.
Метод Ньютона
Классический метод Ньютона полагается на решение на каждой итерации системы линейных уравнений с матрицей Гессе в левой части. При возможности используется коэффициент в одномерном поиске. Любая матрица Гессе симметрична. Если дополнительно предположить, что она положительно определена (SPD), то созданное направление является наравлением спуска, что несложно показать напрямую:
Если известно, что число обусловленности матрицы Гессе равноверно ограничено, т.е. существует константа такая, что для всех , то , и, cледовательно, глобальная сходимость гарантируется в случае матрицы Гессе из класса SPD. Однако матрица Гессе не является SPD для невыпуклой функции во всей области её определения. В таких случаях используют разнообразные методы для корретикровки собственных значений матрицы Гессе, до тех пор, пока участки положительной определённости в пространстве переменных не будут достигнуты, так чтобы потом итерации могли продолжать свою работу с настоящей матрице Гессе. Такие методы относятся к классу модифицированного метода Ньютона, и затрагивать здесь мы их не будем.
Несмотря на отсутствие глобальной сходимости стандартного метода Ньютона для общего класса функций, преимущество его использования заключается в квадратичной скорости сходимости вблизи минимизатора. Вблизи минимизатора выбор сразу же удовлетворяет условиям Вульфа. Метод также инвариантен по отношению к масштабированию задачи, что является безусловным плюсом. Естественно, необходимость вычислять и сохранять в памяти матрицу Гессе, а также решать линейные системы на каждом шаге, во многих случаях не делает метод Ньютона напрямую доступным на практике.
Откуда шаг в методе Ньютона берётся? Из полиномиальной аппроксимации второго порядка для функции в окрестности точки . Мы просто заменяем функцию её квадратичным многочленом Тейлора и ищем для него минимум, предполагая, конечно, что этот многочлен выпуклый:
Вот одномерный пример, в котором красная парабола есть квадратичное приближение к целевой функции, имеющей синий график:
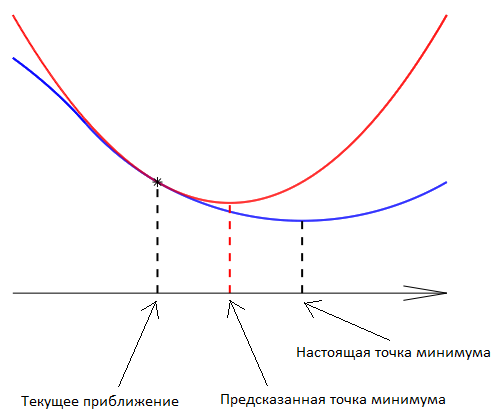
Метод Ньютона является антиподом наискорейшего спуска: иногда он не может углядеть яму с минимизатором, но, найдя её, он быстро «хватает» свою цель. В чистом виде, это «близорукий» метод.
Методы квази-Ньютона
Этот класс методов пытается воспользоваться преимуществами высокой скорости сходимости исходного метода Ньютона, в то же время избегая прямого вычисления матрицы Гессе, а иногда даже решения линейной системы, показанной выше. Вычисление направления в этом случае может быть условно описано как с некоторой приближённой обратной матрицей Гессе.
В методах семейства Бройдена используются некоторые эвристические условия (такие как, например, уравнение секущей) для аппроксимации фактической матрицы Гессе или её обратной таким способом, который желателен для сходимости. Наиболее известные методы из этого семейства — DFP, BFGS, SR1, при этом BFGS является среди них признанным лидером. Построение обратной матрицы Гессе в соответствии с алгоритмом BFGS сохраняет симметрию и положительную определённость матрицы при условии выполнения условий Вульфа на каждой итерации. Последнее требование важно, так как эти условия сильно привязаны к построению матрицы. Следовательно, BFGS гарантирует направление спуска. Однако мало что известно об ограниченности числа обусловленности построенной матрицы для общего класса целевых функций, и поэтому известные теоретические результаты о глобальной сходимости довольно узкие (в частности, они требуют выпуклости функции). Тем не менее, BFGS оказался очень надёжным методом на практике. Кроме того, он обладает сверхлинейной сходимостью, хотя квази-ньютоновские методы в этом отношении все ещё уступают чистому методу Ньютона.
Общее преимущество методов семейства Бройдена заключается в отсутствии необходимости вычислять фактическую матрицу Гессе. Матрица строится исключительно на основе информации о градиенте на предыдущем и текущем шагах. Метод не требует масштабирования, как и метод Ньютона.
SR1 не гарантирует, что его приближённые матрицы Гессе являются положительно определёнными, но, похоже, он хорошо работает в рамках методов доверительной области, где приближённые неопределённые матрицы Гессе могут быть даже предпочтительнее. Мы вернёмся к технике SR1 в случае, если я напишу пост о методах доверительной области.
Покажем наконец формулы для обновления приближённой обратной матрицы Гессе в соответствии с методом BFGS:
Обратите внимание на то, что член всегда положителен при выполнении условия кривизны в неравенствах Вульфа.
Завершим эту секцию обсуждением геометрического смысла квази-ньютоновского приближения матрицы Гессе в одномерном случае. С геометрической точки зрения, квази-ньютоновские методы реализуют обычный метод секущих для решения уравнения . Действительно, шаг Ньютона для оптимизации одномерной целевой функции записывается как Обозначим . Мы, в результате, ищем корень функции , т.е. решение уравнения , методом Ньютона Метод секущих заменяет производную тангенсом угла секущей, построенной на двух ближайших приближениях:
См. рисунок с итерациями на графике :
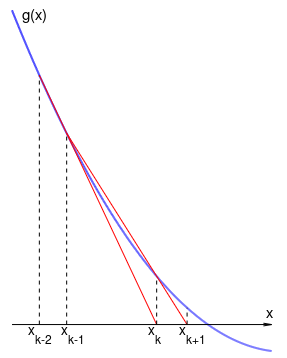
Это и порождает квази-ньютоновский алгоритм оптимизации (правда, в данном случае, с фиксированным шагом поиска ):
Приглушённый BFGS
В случае, если условия Вульфа не выполняются на каком-то шаге , мы не можем быть уверены, что наша следующая матрица Гессе, полученная с помощью формулы BFGS, будет положительно определённой. Это может нарушить глобальную сходимость метода линий. Чтобы избежать этой проблемы, можно расширить формулу BFGS на более общий случай, как показано ниже.
Обозначим , где означает приближённую SPD-матрицу Гессе на итерации . Член теперь может иметь любой знак, в то время как член строго положителен. Рассмотрим
и .
Тогда формула обновления приближённой матрицы Гессе (не её обратной, как в случае с оригинальным BFGS) следующая:
Эта формула, называемая формулой приглушённого BFGS (damped BFGS), обеспечивает положительную определённость матрицы . Релевантность подобной аппроксимации — тема для дебатов, но, по крайней мере, направление спуска будет сохранено (Подобные трюкачества с изменением матрицы Гессе, искажающие аппроксимацию, происходят и в модифицированном методе Ньютона ради достижения направления спуска, см. выше ). Эту формулу можно пытаться использовать для поиска минимизатора самой общей невыпуклой целевой функции в рамках метода линий.
Метод нелинейных сопряжённых градиентов (NCG)
Методы класса NCG в некотором смысле уникальны. Они возникли из прямой адаптации традиционного метода сопряжённых градиентов (CG) для решения линейных SPD-систем к нелинейной оптимизации.
Методы NCG являются единственными в этом списке, которые строят текущее направление на основе предыдущего: . Все методы в пределах этого класса в основном различаются тем, как задаётся скалярный параметр . Они так или иначе используют информацию о текущем и предыдущем градиентах при вычислении . Идея NCG принадлежит авторам Fletcher-Reeves (FR). Последующие модификации предложены следующими авторами: Polac-Rabier (PR), Hestenes-Stiefel (HS), Dai-Yuan (DY), Hager-Zhang (HZ). Если также модификации с обозначениями PR+, FR-PR.
Результаты по глобальной сходимости весьма неопределённы. Для FR наилучший результат по сходимости заключается в том, что последовательность магнитуд не отделена от нуля (т.е. нижний предел последовательности равен нулю), но ничего не говорится о том, существует ли сам предел, равный нулю. Что касается PR, даже если на практике он работает лучше, чем FR, теоретические результаты по нему ещё хуже, поскольку для него был построен расходящийся пример с специальной, но достаточно гладкой целевой функцией. FR гарантирует направление спуска до тех пор, пока выполняются строгие условия Вульфа с параметрами . Но с практической точки зрения FR является наихудшим методом, так как он может стагнировать из-за почти прямого угла между градиентом и направлением спуска и никогда не выйти из этой стагнации. Его можно улучшить, выполняя перезапуски (restarts), т.е. полагая всякий раз, когда обнаруживается близкий к прямому угол. Это заменяет направление FR на направление по антиградиенту.
Методы PR+ и HS гарантируют направление спуска, но требуют выполнения так называемого условия достаточного спуска во время одномерного поиска. Для DY и HZ сильных условий Вульфа достаточно для генерации направления спуска на следующей итерации, и эти два метода по сей день остаются одними из самых надежных.
Методы NCG часто рекомендуют использовать только для крупномасштабных задач ввиду их дешевизны, поскольку они менее устойчивы по сравнению с другими методами линий. Они не требуют хранения матрицы в памяти, и считается, что они в целом сходятся быстрее, чем метод наискорейшего спуска. Скорость сходимости NCG обычно линейна, но в некоторых работах была показана квадратичная или даже так называемая суперквадратичная -сходимость. Некоторое масштабирование для NCG может быть предпочтительным.
Ниже приведём формулы для для упомянутых методов из класса NCG:
- FR:
- PR:
- HS:
- DY:
- HZ:
В последней формуле , как и для формулы BFGS.
Усечённый метод Ньютона (truncated Newton method)
Для крупных задач, даже если матрица Гессе у нас в наличии и используются методы для решения разреженных систем линейных уравнений, часто бывает слишком сложно вычислить шаг Ньютона «в лоб». По этой причине на сцену выходит итерационный линейный решатель, такой как метод сопряженных градиентов (CG, см. упоминание выше). Это даёт начало семейству так называемых неточных, или усечённых, методов Ньютона (не путать с модифицированным). Критерием останова CG в этом случае будет с некоторой точностью .
Этот метод имеет сверхлинейную скорость сходимости при соблюдении определённых условий. Поскольку решатель CG сходится только для матриц SPD, неточный метод Ньютона адаптирует CG так, чтобы тот обрывал итерации сразу после обнаружения отрицательной кривизны (т.е. попадает в зону невыпуклости функции), и затем использует полученное, «обрезанное» направление спуска.
Явное знание матрицы Гессе не требуется, поскольку в итерационных решателях требуется знать только результат произведения матрицы на вектор. Такое произведение можно аппроксимировать с помощью автоматического дифференцирования или метода конечных разностей, применяемого к градиенту вдоль необходимого нам направления. Например, самая простая конечная разность — первого порядка точности — может выглядеть вот так:
Недостатком усечённого метода Ньютона является его плохая сходимость для почти сингулярных или плохо обусловленных матриц Гессе (что верно и для обычного метода Ньютона). Жетально ли для усеченного метода Ньютона масштабирование, я до конца не уверен.
Усечённый метод Ньютона я бы отнёс к гибридным методам. Во-первых, вдали от решения он проводит глобализацию — уверенно ищет зону расположения точки минимума. Делается это как раз благодаря избеганию отрицательной кривизны, причём самая первая и единственная итерация СG в этом случае выполняется как при наискорейшем спуске, что и помогает глобальной сходимости. Во-вторых, найдя эту зону с точкой минимума, включается вся мощь метода Ньютона с его быстрой хваткой.
BFGS c ограниченной памятью
BFGS c ограниченной памятью, также известный как L-BFGS, является адаптацией стандартного метода BFGS для задач с большим количеством переменных. Проблема стандартного BFGS, как и остальных квази-ньютоновских методов, в том, что обновление матрицы Гессе или её обратной на каждом шаге использует внешнее произведение плотных векторов. Имеется в виду произведение вертикального вектора на горизонтальный, например, вот так: (см. формулу BFGS выше). Такое произведение генерирует плотную матрицу. По этой причине, из-за быстрого расхода памяти с ростом размерности задачи, была разработана экономичная версия BFGS.
В основе этой версии лежит запись последовательности разностей градиентов и координат из последних итераций, где обычно принимает значение от 3 до 20. В процессе расчёта квази-ньютоновского направления , обновление матрицы заменяется конкретной рекурсивной формулой произведения матрицы на вектор градиента с использованием заданной последовательности на каждом шаге. После этого последовательность обновляется путём удаления самой старой пары и добавления в очередь новой пары. По сути мы сохраняем память, немного жертвуя производительностью за счёт прикручивания двух циклов на каждой итерации метода.
L-BFGS точно воспроизводит процедуру BFGS, как если бы она применялась для последних шагов, начиная с заданного начального матричного приближения. Это приближение предоставляется специальным образом.
Вот скетч алгоритма L-BFGS для вычисления .
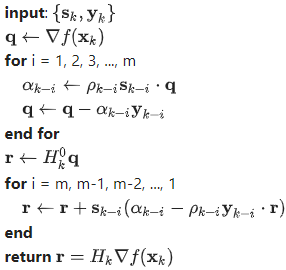
В алгоритме выше член означает .
Несмотря на то, что L-BFGS плохо себя ведёт для плохо обусловленных задач (с широким распределением собственных значений в истинной матрице Гессе), он часто является удовлетворительным методом для задач безусловной минимизации с большим количеством переменных. Существуют и другие квази-ньютоновские методы с ограниченной памятью, но они мне кажутся менее популярными, чем L-BFGS.
Итог
Подытожим. В таблице ниже представлены описанные выше методы с точки зрения 6 характеристик, которые для нас представляли интерес.
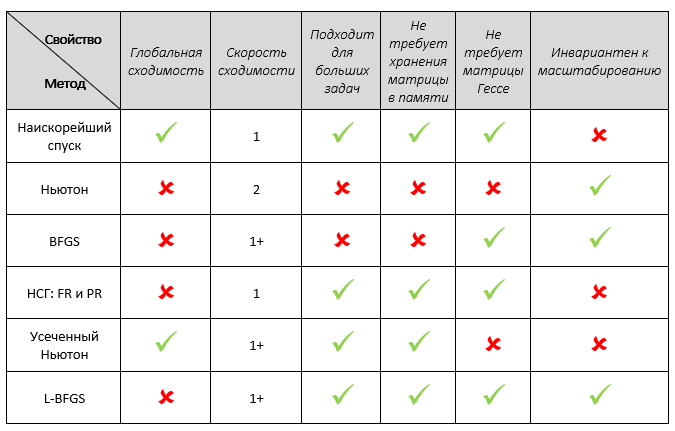
Оговорюсь, не в 100% пунктов выше я уверен, например, что касается масштабирования, но в целом, думаю, таблица достаточно информативная.
Примеры
Рассмотрим два кейса для минимизации в :
- , начальное приближение , глобальный минимизатор .
- , начальное приближение , два глобальных минимизатора , .
В втором кейсе есть участки невыпуклости функции, что должно создать дополнительные трудности для оптимизатора. Точка в этом примере является стационарной (более конкретно — седловой), поэтому наше начальное приближение немного сдвинуто от неё, однако оно расположено в зоне невыпуклости.
Критерием остановки мы в обоих случаях полагаем .
Мы посмотрим, как сработают три алгоритма метода линий: наискорейший спуск, BFGS, FR. Последний мы используем с перезапуском: при нарушении условия , где есть угол между и , мы полагаем .
Вот такие параметры мы использовали для одномерной минимизации:
| Метод | Наискорейший спуск | BFGS | FR |
|---|---|---|---|
| Условие Вульфа | сильное | стандартное | сильное |
Первый кейс
Наискорейший спуск, 9 итераций:
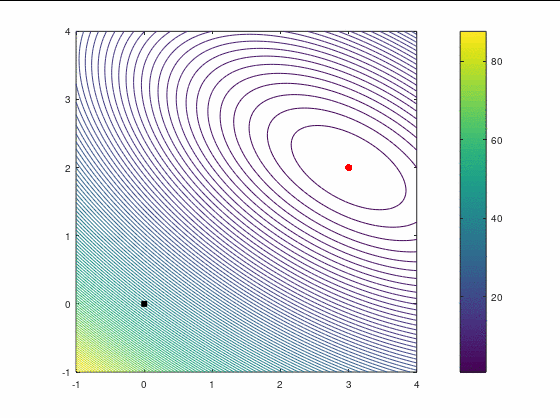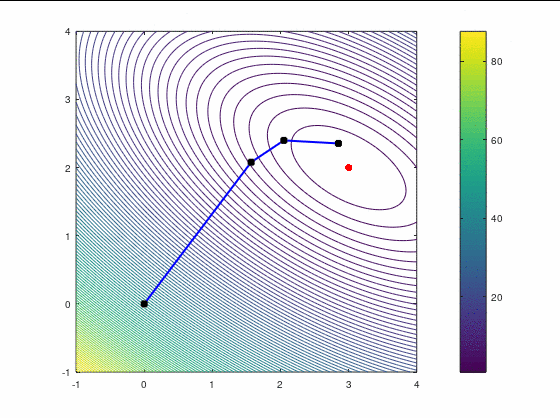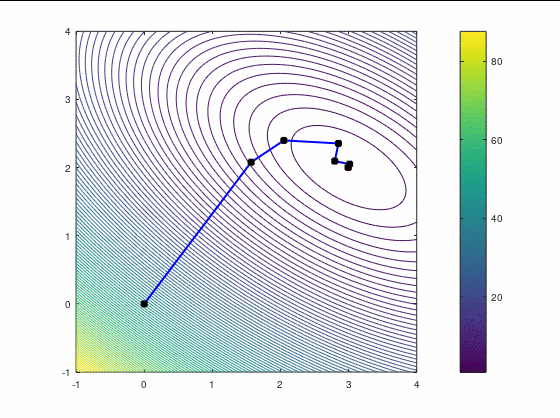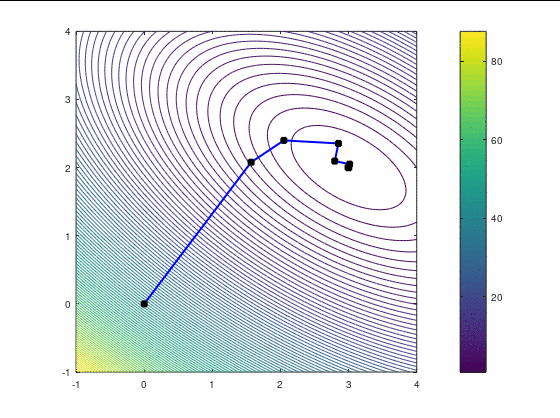
BFGS, 7 итераций (ожидаемо чуть увереннее, чем наискорейший спуск, на выпуклой функции):
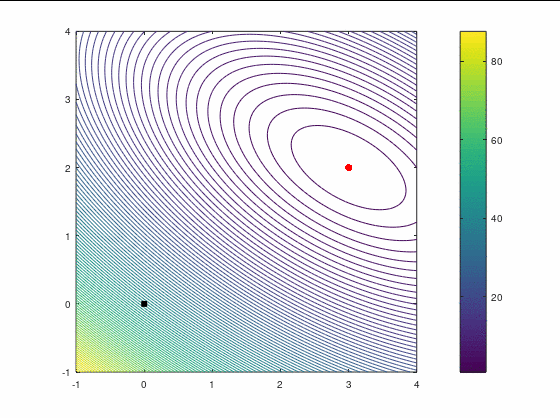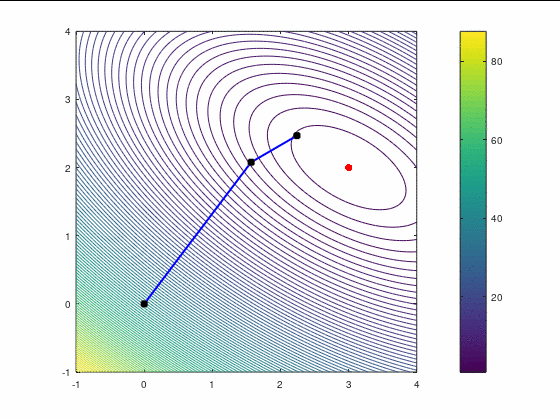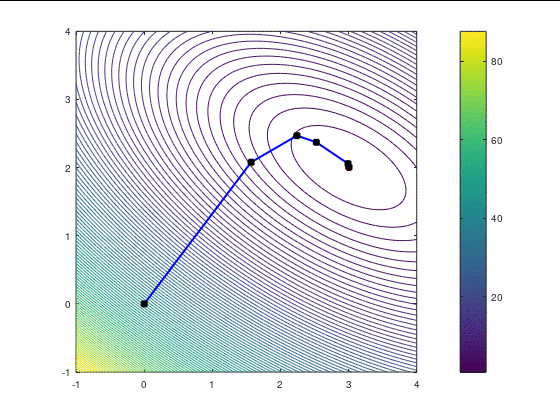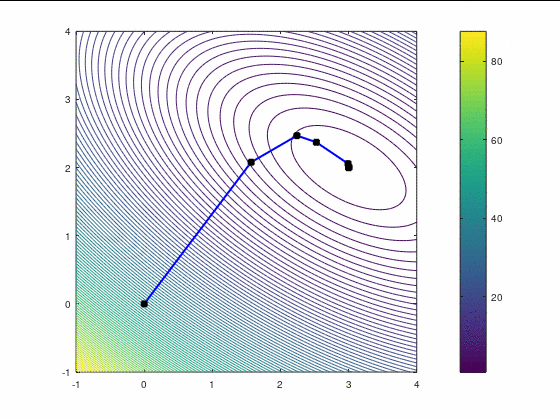
FR, 14 итераций:
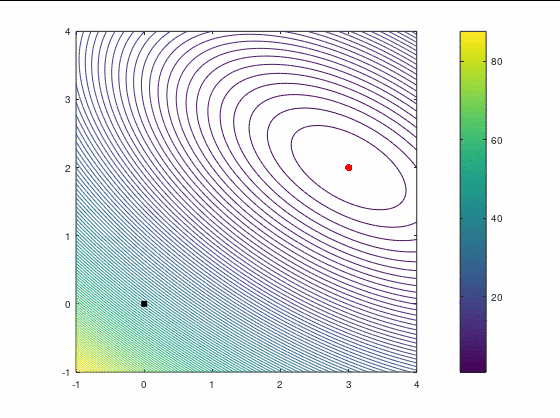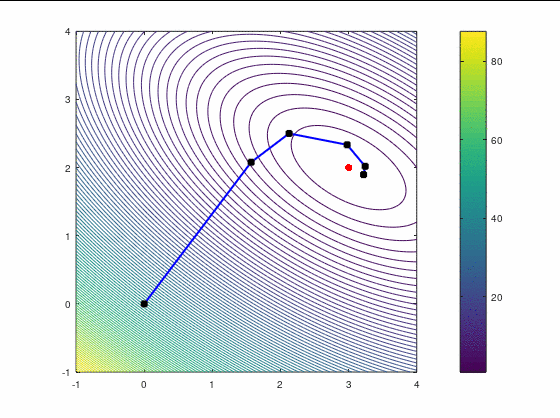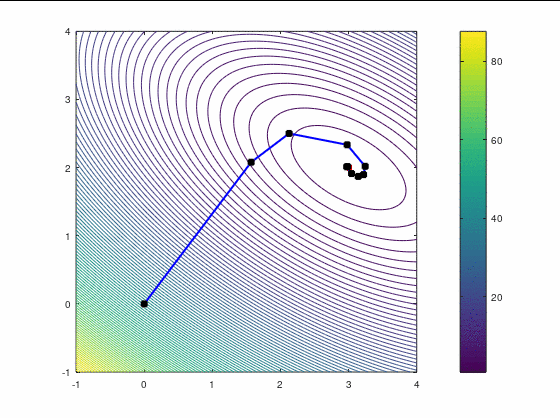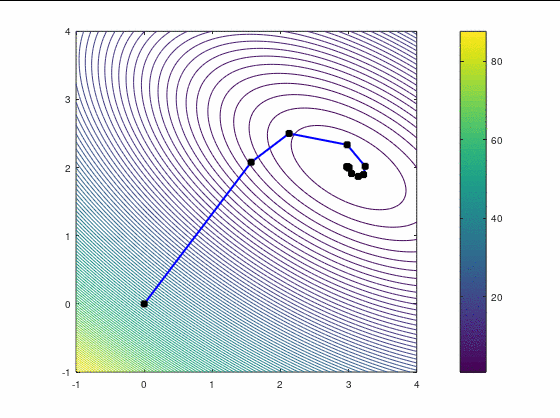
Второй кейс
Наискорейший спуск, 14 итераций:
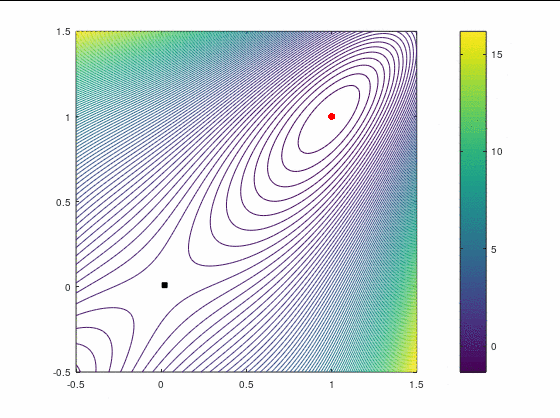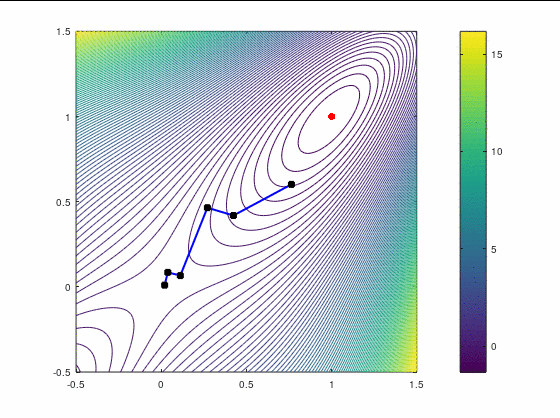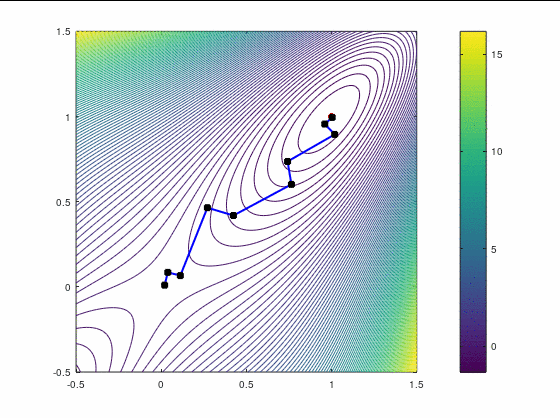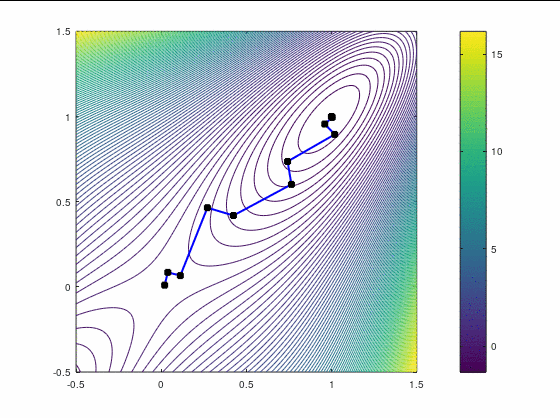
BFGS, 15 итераций:
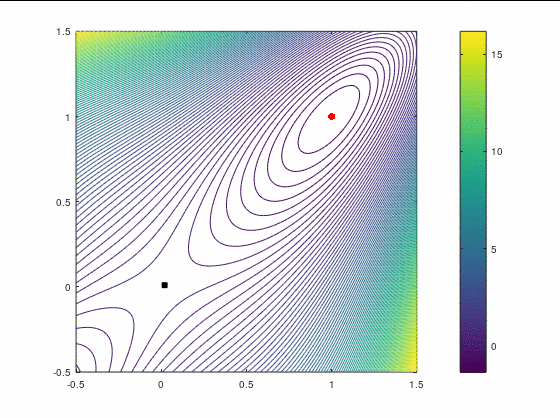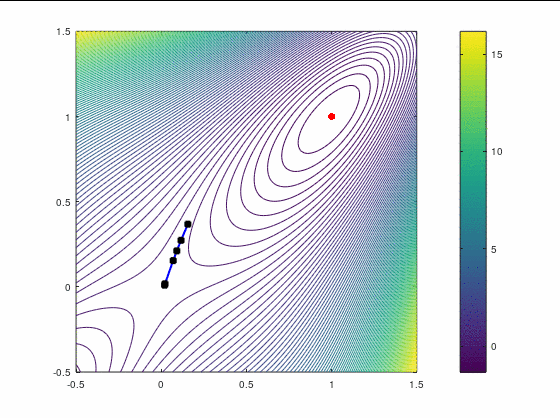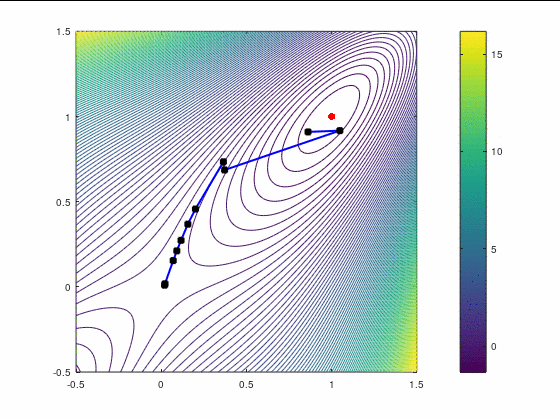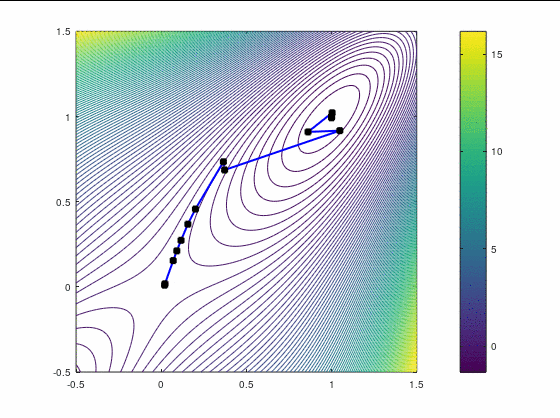
FR, 25 итераций:
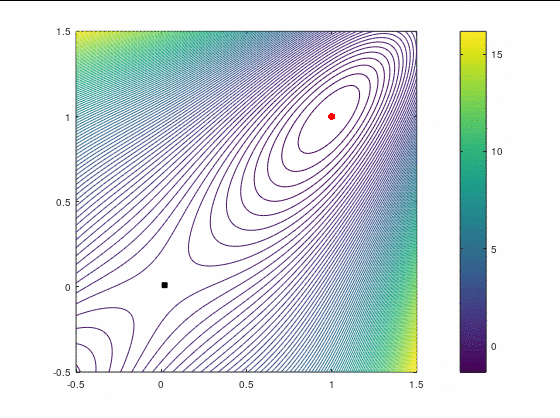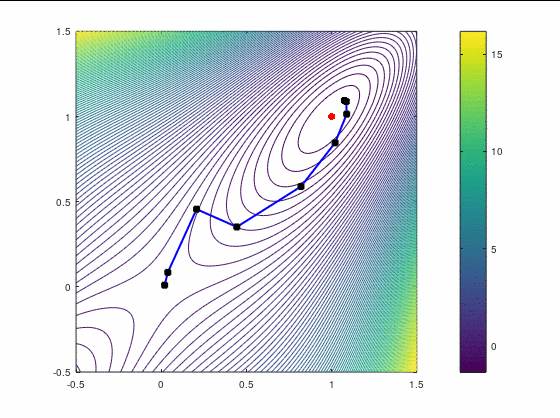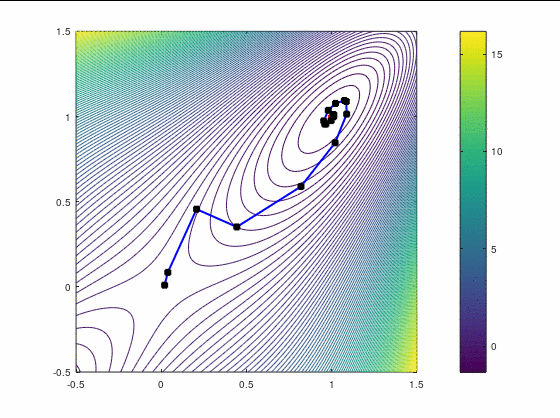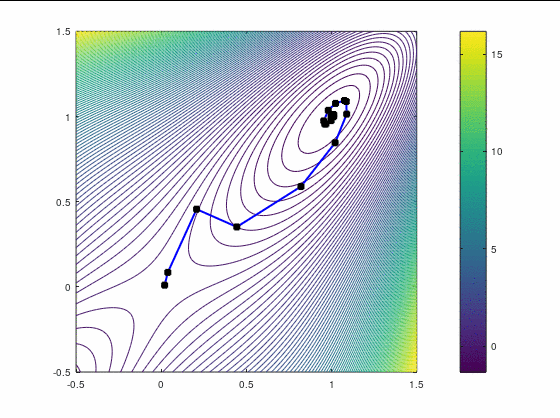
В обоих случаях, FR потребовал больше итераций, чем даже наискорейший спуск, хотя необходимость перезапуска возникла только раз — на третьей итерации в втором кейсе. Также ни в одном из двух кейсов BFGS не потребовал приглушения, т.к. нам удалось на каждой итерации удовлетворить условию Вульфа.
В будущем, если ничто не помешает, хотел бы продолжить эту тему. Следующий кандидат на очереди — метод доверительной области (trust-region method).
А на горизонте маячит условная оптимизация.
Всем добра!
Список литературы
(Разумеется, список далеко не полный)[1] Аттетков, А. В., Галкин, С. В., & Зарубин, В. С. (2001). Методы оптимизации. Изд. МГТУ им. Баумана.
[2] Nocedal, J., Wright, S. J., Numerical Optimization. Second Edition. Springer 2006.
[3] More, J. J., Newton’s method. Studies in Numerical Analysis, MAA Studies in Mathematics, 24 (1984): 29–82.
[4] Gill P.E., Murray W., Wright M. H., Practical Optimization, Academic Press, 1981.
[5] Powell M. J. D., Some global convergence properties of a variable metric algorithm for minimization without exact line searches, Nonlinear Programming, SIAM-AMS Proceedings, R. W. Cottle and C. E. Lemke, eds., SIAM Publications, IX(1976): 53–72.
[6] Fletcher R., Reeves C. M., Function minimization by conjugate gradients, Computer Journal, 7 (1964): 149–154.
[7] Dai Y., Yuan Y., A nonlinear conjugate gradient method with a strong global convergence property, SIAM Journal on Optimization, 10 (1999): 177–182.
[8] Hager W. W., Zhang H., A new conjugate gradient method with guaranteed descent and an efficient line search, SIAM Journal on Optimization, 16 (2005): 170–192.
[9] Al-Baali M., Descent property and global convergence of the Fletcher-Reeves method with inexact
line search, I.M.A. Journal on Numerical Analysis, 5 (1985): 121–124.
[10] Powell M. J. D., Nonconvex minimization calculations and the conjugate gradient method, Lecture Notes in Mathematics, 1066 (1984): 122–141.
[11] Gilbert J., Nocedal J., Global convergence properties of conjugate gradient methods for optimization, SIAM Journal on Optimization, 2 (1992): 21–42.


omxela
Тема замечательная, одна из моих любимых. С интересом освежил, спасибо. По этому поводу и написано много, что скрывать. И вот я бы сделал упор не на тех случаях, когда эти методы эффектно работают. А на тех, когда возникают трудности и алгоритм заходит "не туда". Иначе возникает ощущение, что вот есть функция, задвинем ее, скажем, в метод градиентного спуска - и готово дело. Пара слов была сказана: про невыпуклость, и про разброс СЗ. Но как-то вскользь. А есть еще овраги. Есть супер узкие воронки, где на конечной разрядной сетке можно вылететь с поверхности. И так далее.
MajinSaha Автор
Спасибо. По поводу незахода метода «не туда» конечно всё зависит от конкретного случая и требует отдельного разбирательства. Однако я надеюсь, что снял часть вопросов за счёт обсуждения глобальной сходимости — той концепции, которую, как мне показалось, другие авторы по оптимизации обычно не затрагивают. Конкретно для метода градиентного спуска, если функция гладкая и одномерный поиск делается с «головой», то зайти «не туда» он не может! Как я написал выше, он «король» глобальной сходимости. И это касается и невыпуклых функций в том числе.
Но я не спорю, что часто дело касается не самой математики, а реализации на практике. Даже теоретически хорошие функции в коде могут быть реализованы кривовато и/или давать существенную ошибку и препятствовать хорошей работе одномерного поиска, что вредит сходимости. Тут уж общих рецептов у меня нет.