Недавно я написал непобедимую игру «Крестики-Нолики». Это был интересный и поучительный проект, который многому меня научил. Если у вас есть желание посмотреть результат — это можно сделать здесь.
Для того чтобы сделать игру непобедимой, было необходимо создать алгоритм, который может рассчитать все возможные ходы для «компьютерного» игрока. Далее, нужно использовать некоторую метрику, чтобы определить, какой ход является предпочтительным. После долгих исследований стало понятно, что алгоритм Минимакс, был тем, что мне нужно.
Понимание основ алгоритма и реализация игры заняли некоторое время. Я нашел много примеров кода и объяснений, тем не менее это оказалось не такой уж простой затеей. Надеюсь этот пост поможет некоторым из читателей оценить элегантность этого алгоритма.
Для начала давайте опишем, что мы понимаем под «идеальной» игрой — если я играю идеально, я или побеждаю в игре, или играю вничью. В случае если я играю против другого «идеального» игрока, я всегда играю вничью.
Можно ли описать эти требования количественно? Давайте для всех возможных вариантов конечного состояния игры назначить какое-то количество очков:
Теперь мы можем количественно оценить любое конечное состояние игры.
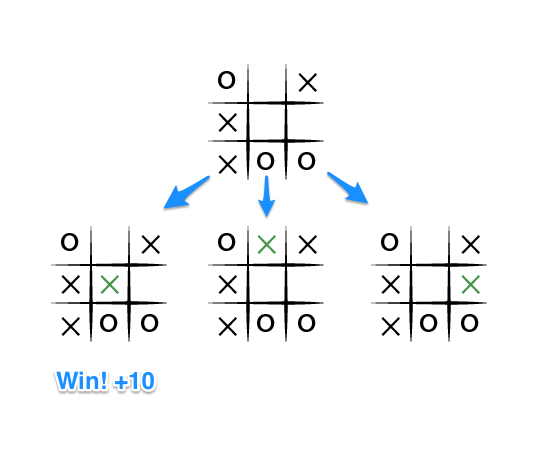
На картинке изображено состояние игрового поля, и мой черед ходить. Я играю за «Х». Моя цель, очевидно, максимизация количества очков, которые я получу.

Верхняя часть картинки показывает состояние игры, и, в зависимости от моего выбора, я могу попасть в одно из трех состояний из нижней части картинки. Очевидно, что состояние, в котором я побеждаю (снизу слева) является наилучший. Если я не сделаю этот ход, игрок «О» может легко победить, и я не хочу, чтоб он победил. Таким образом, выберу ход, который принесет мне наибольшее число очков.
Но что мы знаем о втором игроке? Мы можем предположить, что он тоже играет с целью победить в игре. Игрок «О» хочет выбрать ход, который приведет к наименьшему выигрышу для нас, он хочет минимизировать наш выигрыш. Давайте посмотрим на вещи с точки зрения игрока «О» начиная с двух других состояний игры из предыдущего примера, тех, в которых я не побеждаю:
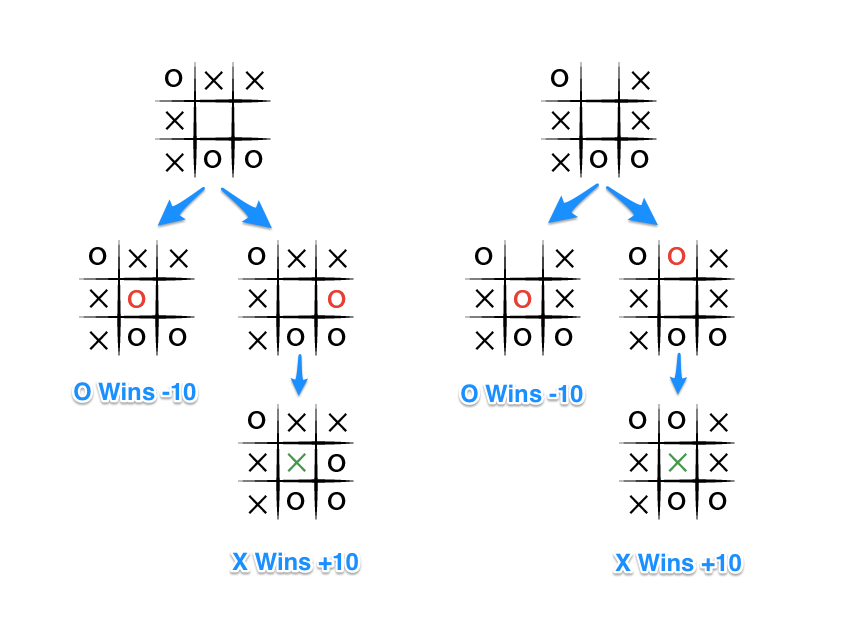
Выбор очевиден, «О» выберит один из ходов, который приведет нас к результату -10.
Суть алгоритма Минимакс это поочередный перебор возможных ходов двух игроков, при котором мы считаем, что игрок «чья очередь» выберет ход, приносящий максимальное количество очков. Предположим, что мы играем за игрока «Х», тогда описание алгоритма будет примерное таким:
Алгоритм является рекурсивным, и расчёт производится по очереди для каждого из игроков до тех пор, пока не рассчитан финальный выигрыш. Давайте посмотрим, как алгоритм работает с полным деревом ходов, и посмотрим, как будет выбран наилучший ход:

Как видите, здесь немалое количество вычислений, и именно поэтому нам нужен компьютер, чтоб применить этот алгоритм.
Надеюсь теперь у вас есть общее представление, как алгоритм Минимакс определяет наилучший ход. Давайте рассмотрим имплементацию алгоритма, чтоб закрепить наше понимание.
Вот функция, которая производит оценку состояния:
Достаточно просто, вернуть +10 если текущий игрок побеждает в игре, -10, если проигрывает и 0 в случае ничьи. Вы также можете отметить, что с точки зрения алгоритма нет разницы, какой это игрок (»Х" или «О»), важно лишь чей ход.
А теперь собственно сам алгоритм; обратите внимания что в приведенном варианте выбор хода это просто адрес ячейки на поле, т.е. [0,2] это правая верхняя ячейка на игровом поле размером 3x3.
Когда алгоритм выполняется в классе PerfectPlayer, выбор наилучшего ходя сохраняется в переменной choice, которая впоследствии используется для того, чтобы вернуть новое состояние игры в которое мы попадаем в результате выбранного игроком хода.
Эта имплементация алгоритма позволит вам создать игру в «крестики-нолики», в которую вы не сможете победить. Но есть маленький нюанс, который я обнаружил в процессе тестирования игры. В случае, если мой «идеальный игрок» обнаружит состояние, в котором он или проиграет, или закончит вничью, его ход будет самоубийственным. Проще говоря, алгоритм говорит «я все равно проиграю, поэтому без разницы сейчас, или через 6 ходов».
Я обнаружил это когда передал явно некорректное состояние игрового поля и попытался выяснить, какой ход предложит алгоритм. Я ожидал, что «идеальный игрок» попытается помешать мне выиграть так долго, как сможет, но этого не произошло:
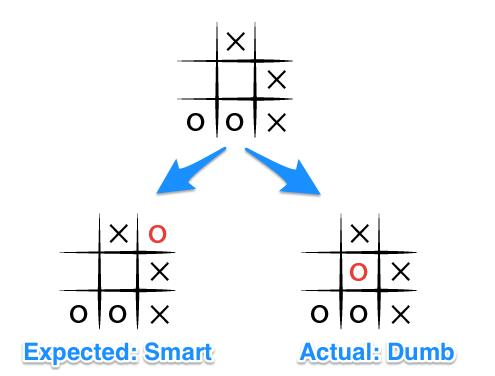
Давайте рассмотрим, что происходит здесь через призму возможных ходов (для простоты я удалил некоторые состояния)

В результате данных расчетов, принимая во внимание факт, что при расчёте выигрыша мы итерируемся слева направо, снизу вверх, не проводя различий между ходами, будет выбран ход, приводящий в состояние 5, так как это последний доступный ход из состояния 1.
Черт побери, что же мастер «крестиков-ноликов» должен сделать?
Наилучшим улучшением для алгоритма будет изменить его так, чтоб «идеальный игрок» играл «идеально» до самого конца, т.е. взять «глубину» (количество ходов до возможного проигрыша) в расчет при выборе хода. Простыми словами, идеальный игрок будет играть идеально, и постарается играть так долго, как только сможет.
Для того чтобы достигнуть такого результата мы будем отнимать глубину рекурсии\количество ходов от конечного состояния игры. Т.е. чем больше ходов до минимального выигрыша (и чем меньше ходов до максимального) — тем лучше.
Так, каждый раз при вызове алгоритма Минимакс глубина будет увеличена на 1, и когда мы наконец рассчитаем возможный выигрыш для конкретного конечного состояния игры мы введем поправку на глубину. Давайте посмотрим, как это выглядит на примере следующего дерева ходов:

Теперь учет глубины (как показано черным слева) приводит к тому, что оценка различается для каждого конечного состояния, и, потому что на первом уровне Минимакс будет пытаться максимизировать возможный выигрыш (т.к. ход игрока «О») предпочтительная оценка выигрыша составит -6, т.к. это выше чем альтернативный вариант в -8. И потому, несмотря на то, что игроку грозит верная смерть, наш надежный «идеальный игрок» выберет ход, который приведет к достойной смерти, и заблокирует выигрыш игрока «Х».
Я надеюсь все эти пояснения помогли вам получше понять алгоритм Минимакс, и, возможно, как можно всегда выигрывать в «крестики-нолики». Если у вас есть вопросы, или что-то вам кажется непонятным, напишите, пожалуйста, в комментариях и я улучшу статью. Полный код можно найти у меня на Github. А поиграть в получившуюся игру можно здесь: http://perfecttictactoe.herokuapp.com/.
Перевод сделан с разрешения автора. Мне понравилась эта статья тем, что она просто и наглядно описала алгоритм Минимакс. В статье присутствуют неточности и упрощения а также, местами, неточная терминология.
Возможно вам также будет интересен мой YouTube канал.

Для того чтобы сделать игру непобедимой, было необходимо создать алгоритм, который может рассчитать все возможные ходы для «компьютерного» игрока. Далее, нужно использовать некоторую метрику, чтобы определить, какой ход является предпочтительным. После долгих исследований стало понятно, что алгоритм Минимакс, был тем, что мне нужно.
Понимание основ алгоритма и реализация игры заняли некоторое время. Я нашел много примеров кода и объяснений, тем не менее это оказалось не такой уж простой затеей. Надеюсь этот пост поможет некоторым из читателей оценить элегантность этого алгоритма.
Описание «Идеальной» игры «Крестики-Нолики»
Для начала давайте опишем, что мы понимаем под «идеальной» игрой — если я играю идеально, я или побеждаю в игре, или играю вничью. В случае если я играю против другого «идеального» игрока, я всегда играю вничью.
Можно ли описать эти требования количественно? Давайте для всех возможных вариантов конечного состояния игры назначить какое-то количество очков:
- Я победил, ура! Я получаю 10 очков!
- Я проиграл, блин. Я теряю 10 очков (потому, что другой игрок получает 10 очков).
- Ничья. Я получаю ноль, и другой игрок получает ноль.
Теперь мы можем количественно оценить любое конечное состояние игры.
Давайте рассмотрим короткий пример.
На картинке изображено состояние игрового поля, и мой черед ходить. Я играю за «Х». Моя цель, очевидно, максимизация количества очков, которые я получу.

Верхняя часть картинки показывает состояние игры, и, в зависимости от моего выбора, я могу попасть в одно из трех состояний из нижней части картинки. Очевидно, что состояние, в котором я побеждаю (снизу слева) является наилучший. Если я не сделаю этот ход, игрок «О» может легко победить, и я не хочу, чтоб он победил. Таким образом, выберу ход, который принесет мне наибольшее число очков.
Но что мы знаем о втором игроке? Мы можем предположить, что он тоже играет с целью победить в игре. Игрок «О» хочет выбрать ход, который приведет к наименьшему выигрышу для нас, он хочет минимизировать наш выигрыш. Давайте посмотрим на вещи с точки зрения игрока «О» начиная с двух других состояний игры из предыдущего примера, тех, в которых я не побеждаю:

Выбор очевиден, «О» выберит один из ходов, который приведет нас к результату -10.
Описание алгоритма Минимакс
Суть алгоритма Минимакс это поочередный перебор возможных ходов двух игроков, при котором мы считаем, что игрок «чья очередь» выберет ход, приносящий максимальное количество очков. Предположим, что мы играем за игрока «Х», тогда описание алгоритма будет примерное таким:
- Если игра закончена, вернуть количество очков для игрока «Х»
- В противном случае, получить список новых состояний игровой области для каждого возможного хода
- Оценить возможный выигрыш для каждого возможного состояния
- Для каждого из возможных состояний добавить «Минимакс» оценку текущего состояния
- Если ход игрока «Х» — вернуть ход с максимальным количеством очков
- Если ход игрока «О» — вернуть ход с минимальным количеством очков
Алгоритм является рекурсивным, и расчёт производится по очереди для каждого из игроков до тех пор, пока не рассчитан финальный выигрыш. Давайте посмотрим, как алгоритм работает с полным деревом ходов, и посмотрим, как будет выбран наилучший ход:

- В состоянии 1 — очередь ходить у игрока «Х». «Х» генерирует состояния 2, 3 и 4 и рекурсивно применяет алгоритм к сгенерированным состояниям
- Состояние 2 добавляет выигрыш в размере +10 к оценке состояния 1, потому что игра выиграна
- Состояния 3 и 4 не являются конечными состояниями, поэтому из состояния 3 генерируются состояния 5 и 6, из состояния 4 генерируются состояния 7 и 8, после чего к каждому из сгенерированных состояний применяется алгоритм Минимакс.
- Состояние 5 добавляет «проигрыш в размере -10 для состояния 3, то же самое происходит и с состоянием 7 для состояния 4.
- Состояния 6 и 8 генерируют лишь конечные выигрышные состояния, поэтому каждое из них добавляет выигрыш в размере +10 для состояний 3 и 4.
- Так как на состояниях 3 и 4 очередь ходить игрока „О“, „О“ будет искать наименьший выигрыш. Исходя из выбора в -10 и +10, оба состояния вернут -10
- Наконец, оценка выигрыша для состояний 2, 3 и 4 будет рассчитана как +10, -10 и -10 соответственно. Так как игрок „Х“ стремиться максимизировать выигрыш, будет сделан выбор в пользу состояния 2.
Как видите, здесь немалое количество вычислений, и именно поэтому нам нужен компьютер, чтоб применить этот алгоритм.
Реализация алгоритма Минимакс
Надеюсь теперь у вас есть общее представление, как алгоритм Минимакс определяет наилучший ход. Давайте рассмотрим имплементацию алгоритма, чтоб закрепить наше понимание.
Вот функция, которая производит оценку состояния:
# @player is the turn taking player
def score(game)
if game.win?(@player)
return 10
elsif game.win?(@opponent)
return -10
else
return 0
end
end
Достаточно просто, вернуть +10 если текущий игрок побеждает в игре, -10, если проигрывает и 0 в случае ничьи. Вы также можете отметить, что с точки зрения алгоритма нет разницы, какой это игрок (»Х" или «О»), важно лишь чей ход.
А теперь собственно сам алгоритм; обратите внимания что в приведенном варианте выбор хода это просто адрес ячейки на поле, т.е. [0,2] это правая верхняя ячейка на игровом поле размером 3x3.
def minimax(game)
return score(game) if game.over?
scores = [] # an array of scores
moves = [] # an array of moves
# Populate the scores array, recursing as needed
game.get_available_moves.each do |move|
possible_game = game.get_new_state(move)
scores.push minimax(possible_game)
moves.push move
end
# Do the min or the max calculation
if game.active_turn == @player
# This is the max calculation
max_score_index = scores.each_with_index.max[1]
@choice = moves[max_score_index]
return scores[max_score_index]
else
# This is the min calculation
min_score_index = scores.each_with_index.min[1]
@choice = moves[min_score_index]
return scores[min_score_index]
end
end
Когда алгоритм выполняется в классе PerfectPlayer, выбор наилучшего ходя сохраняется в переменной choice, которая впоследствии используется для того, чтобы вернуть новое состояние игры в которое мы попадаем в результате выбранного игроком хода.
Идеальный игрок-самоубийца
Эта имплементация алгоритма позволит вам создать игру в «крестики-нолики», в которую вы не сможете победить. Но есть маленький нюанс, который я обнаружил в процессе тестирования игры. В случае, если мой «идеальный игрок» обнаружит состояние, в котором он или проиграет, или закончит вничью, его ход будет самоубийственным. Проще говоря, алгоритм говорит «я все равно проиграю, поэтому без разницы сейчас, или через 6 ходов».
Я обнаружил это когда передал явно некорректное состояние игрового поля и попытался выяснить, какой ход предложит алгоритм. Я ожидал, что «идеальный игрок» попытается помешать мне выиграть так долго, как сможет, но этого не произошло:

Давайте рассмотрим, что происходит здесь через призму возможных ходов (для простоты я удалил некоторые состояния)

- В случае если игровое поле в состоянии 1, и оба игрока играют идеально, и компьютер играет на стороне «О», «О» принимает решение идти в состояние 5, что ведет к немедленному проигрышу, когда игрок «Х» переходит в состояние 9.
- Но если «О» заблокирует ход «Х» перейдя в состояние 3, «Х» заблокирует потенциально победный ход «О», как показано в состоянии 7.
- Исходя из этого очевидно, что «Х» победит, как показано в состояниях 10 и 11, несмотря на то, какой ход выберет «О».
В результате данных расчетов, принимая во внимание факт, что при расчёте выигрыша мы итерируемся слева направо, снизу вверх, не проводя различий между ходами, будет выбран ход, приводящий в состояние 5, так как это последний доступный ход из состояния 1.
Черт побери, что же мастер «крестиков-ноликов» должен сделать?
Даем противнику хороший бой: глубина
Наилучшим улучшением для алгоритма будет изменить его так, чтоб «идеальный игрок» играл «идеально» до самого конца, т.е. взять «глубину» (количество ходов до возможного проигрыша) в расчет при выборе хода. Простыми словами, идеальный игрок будет играть идеально, и постарается играть так долго, как только сможет.
Для того чтобы достигнуть такого результата мы будем отнимать глубину рекурсии\количество ходов от конечного состояния игры. Т.е. чем больше ходов до минимального выигрыша (и чем меньше ходов до максимального) — тем лучше.
def score(game, depth)
if game.win?(@player)
return 10 - depth
elsif game.win?(@opponent)
return depth - 10
else
return 0
end
end
def minimax(game, depth)
return score(game) if game.over?
depth += 1
scores = [] # an array of scores
moves = [] # an array of moves
# Populate the scores array, recursing as needed
game.get_available_moves.each do |move|
possible_game = game.get_new_state(move)
scores.push minimax(possible_game, depth)
moves.push move
end
# Do the min or the max calculation
if game.active_turn == @player
# This is the max calculation
max_score_index = scores.each_with_index.max[1]
@choice = moves[max_score_index]
return scores[max_score_index]
else
# This is the min calculation
min_score_index = scores.each_with_index.min[1]
@choice = moves[min_score_index]
return scores[min_score_index]
end
end
Так, каждый раз при вызове алгоритма Минимакс глубина будет увеличена на 1, и когда мы наконец рассчитаем возможный выигрыш для конкретного конечного состояния игры мы введем поправку на глубину. Давайте посмотрим, как это выглядит на примере следующего дерева ходов:

Теперь учет глубины (как показано черным слева) приводит к тому, что оценка различается для каждого конечного состояния, и, потому что на первом уровне Минимакс будет пытаться максимизировать возможный выигрыш (т.к. ход игрока «О») предпочтительная оценка выигрыша составит -6, т.к. это выше чем альтернативный вариант в -8. И потому, несмотря на то, что игроку грозит верная смерть, наш надежный «идеальный игрок» выберет ход, который приведет к достойной смерти, и заблокирует выигрыш игрока «Х».
В заключение
Я надеюсь все эти пояснения помогли вам получше понять алгоритм Минимакс, и, возможно, как можно всегда выигрывать в «крестики-нолики». Если у вас есть вопросы, или что-то вам кажется непонятным, напишите, пожалуйста, в комментариях и я улучшу статью. Полный код можно найти у меня на Github. А поиграть в получившуюся игру можно здесь: http://perfecttictactoe.herokuapp.com/.
От переводчика
Перевод сделан с разрешения автора. Мне понравилась эта статья тем, что она просто и наглядно описала алгоритм Минимакс. В статье присутствуют неточности и упрощения а также, местами, неточная терминология.
Возможно вам также будет интересен мой YouTube канал.


a-tk
А теперь то же самое для открытой сетки с соответствующей длины линией…
numitus2
А в чем проблема? Просто не надо искать финальную комбинацию, а надо как в шахматах просчитывать на 8-12 ходов и максимизировать "очки"