12.09.2021 19:10
madschumacher 11 8500 Источник

Начался новый учебный год, и преподавателям, студентам и школьникам, возможно, требуется (или просто хочется) посмотреть на то, как выглядят орбитальки, на которых сидят электроны в атомах: все эти завораживающие буковки s, p, d, f, и т.д. Да, картинок полно как в учебниках, так и в Интернете, но покрутить орбитальки на картинке не получится, а картинку из учебника/с левого сайта в презентацию/реферат без мороки с лицензией пихать (по-хорошему) не стоит. Поэтому в этом посте мы разберём одну из возможных реализаций рисовалки для этих самых орбиталек.

Саму концепцию того, что такое атомные орбитали я уже разбирал (https://habr.com/ru/post/443232/), то как рисовать эти орбитали при помощи метода Монте-Карло в варианте алгоритма Метрополиса тоже (https://habr.com/ru/post/548704/),

cобственно, вот и сам код рисовалки на Python (с комментариями),
#! /usr/bin/python3

import numpy as np  # NumPy нужен для всего
import argparse     # Это модуль, для "общения" с юзером



# Эта функция даёт значение "орбитали" в некоторой точке пространства
# Орбиталь является суммой трёх угловых компонент с тремя коэффициентами, домноженной на единую 
# радиальную компоненту.
# r  -- это трёхмерный вектор, расположение электрона в пространстве
# n1,n2,n3 -- это трёхмерный вектор степеней x,y,z компонент вектора в угловой части каждой из трёх компонент
# coeff1,coeff2,coeff3 -- это собственно коэффициенты перед угловыми компонентами
# r0 -- это "размер" радиальной части, даваемой выражением exp(-|r|/r0)
def orb(r, n1, n2=None, n3=None, coeff1=1., coeff2=1., coeff3=1., r0 = 1.0):

    # считаем значение угловой компоненты Ang
    Ang = coeff1 * np.prod(np.power(r,n1))
    if not n2 is None:
         Ang += coeff2 * np.prod(np.power(r,n2))
    if not n3 is None:
         Ang += coeff3 * np.prod(np.power(r,n3))

    Arg = np.sqrt(np.dot(r,r))/r0 # это аргумент для радиальной компоненты

    Rad = np.exp(-Arg)   # считаем значение радиальной компоненты орбитали
    
    return  Rad * Ang # ответ -- это произведение радиальной и угловой компонент
    
# данная функция нужна, чтобы сделать название орбитали
# нам нужны только степени угловой компоненты (n) и коэффициент перед ней
def PowToName(n, coeff=1.):
    FunctionName = ""

    # нет угловой компоненты -- нет и функции
    if n is None or coeff is None:
        return ""
        
    # смотрим на знак коэффициента для углового компонента    
    if not coeff is None:
        if coeff > 0:
            FunctionName += "+%.2f"  % coeff
        elif coeff <0:
            FunctionName += "%.2f" % coeff
        else:
            return "" # если коэффициент нулевой, эта компонента ничего и не даёт
    
    # Степень полинома угловой компоненты -- это тип функции (s/p/d/f...), его мы и проверяем
    if np.sum(n) == 0:
        FunctionName += "s"
    elif np.sum(n) == 1:
        FunctionName += "p"
    elif np.sum(n) == 2:
        FunctionName += "d"
    elif np.sum(n) == 3:
        FunctionName += "f"
    elif np.sum(n) == 4:
        FunctionName += "g"
    elif np.sum(n) == 5:
        FunctionName += "h"
    else:
        FunctionName += "X3" # можно пойти и дальше, но кому это нужно?
    
    
    # и показываем какая конкретно радиальная компонента у нас тут есть (естественно, нулевые степени мы не печатаем)
    if n[0]>0:
        FunctionName += "x"
        if n[0] > 1:
            FunctionName += "%i" %  (n[0])
    if n[1]>0:
        FunctionName += "y"
        if n[1] > 1:
            FunctionName += "%i" %  (n[1])
    if n[2]>0:
        FunctionName += "z"
        if n[2] > 1:
            FunctionName += "%i" %  (n[2])
               
    return FunctionName
   


# argument parser to get options from command line
parser = argparse.ArgumentParser(description='Давайте-ка нарисуем орбитальки при помощи метода Монте-Кало (МК)!') 


parser.add_argument('--c1', type=float, default=1.0, 
                    help="Коэффициент перед первой угловой функцией")  


parser.add_argument('--c2', type=float, default=0.0, 
                    help="Коэффициент перед второй угловой функцией")  


parser.add_argument('--c3', type=float, default=0.0, 
                    help="Коэффициент перед третьей угловой функцией")  

parser.add_argument('--nx1', type=int, default=0, 
                    help="Степень n в функции x**n для первой угловой функции") 

parser.add_argument('--nx2', type=int, default=0, 
                    help="Степень n в функции x**n для второй угловой функции") 

parser.add_argument('--nx3', type=int, default=0, 
                    help="Степень n в функции x**n для третьей угловой функции") 

parser.add_argument('--ny1', type=int, default=0, 
                    help="Степень n в функции y**n для первой угловой функции") 

parser.add_argument('--ny2', type=int, default=0, 
                    help="Степень n в функции y**n для второй угловой функции") 

parser.add_argument('--ny3', type=int, default=0, 
                    help="Степень n в функции y**n для третьей угловой функции") 

parser.add_argument('--nz1', type=int, default=0, 
                    help="Степень n в функции z**n для первой угловой функции") 

parser.add_argument('--nz2', type=int, default=0, 
                    help="Степень n в функции z**n для второй угловой функции") 

parser.add_argument('--nz3', type=int, default=0, 
                    help="Степень n в функции z**n для третьей угловой функции") 

parser.add_argument('--NumSteps', type=int, default=50000, 
                    help="Число шагов в МК симуляции") 

parser.add_argument('--R0', type=float, default=1.0, 
                    help="Размер орбитали R0") 

parser.add_argument('--PartToIgnore', type=float, default=0.1, 
                    help="Доля МК траектории в начале, которая игнорируется в расчётах, как стадия уравновешивания") 


parser.add_argument('--MaxBox', type=float, default=0.1, 
                    help="Размер стартовой области, из которой случайно выбирается стартовая точка МК-траектории") 


parser.add_argument('--MaxStep', type=float, default=2.0, 
                    help="Максимальная длина шага в МК-траектории") 


parser.add_argument('--MaxSmallShift', type=float, default=0.1, 
                    help="Маленькая добавочка к значениям траектории, когда мы остаёмся в той же точке (для красоты)") 


parser.add_argument('--plot',action='store_true', 
                    help="Флаг, чтобы нарисовать орбитальку при помощи matplotlib") 



# а теперь распарсим аргументы
args,unknown = parser.parse_known_args()


# составляем вектора из степеней для каждой из трёх угловых функций из того, что ввёл юзер
NPow1 = np.array([args.nx1,args.ny1,args.nz1] ,dtype=int)
NPow2 = np.array([args.nx2,args.ny2,args.nz2] ,dtype=int)
NPow3 = np.array([args.nx3,args.ny3,args.nz3] ,dtype=int)    
        

# выбираем случайную стартовую точку в заданной юзером области пространства (кубике вокруг r=(0,0,0) со стороной 2*MaxBox)
currentR = np.random.uniform(low=-args.MaxBox, high=args.MaxBox, size=3) 
# считаем значение орибитали в этой точке
currentOrbP = orb(r=currentR, n1=NPow1, n2=NPow2, n3=NPow3, coeff1=args.c1, coeff2=args.c2, coeff3=args.c3, r0 = args.R0)

# в этот файл мы будем сохранять саму траекторию
FileName="orbital_%s%s%s.dat" % (PowToName(NPow1, args.c1),PowToName(NPow2, args.c2),PowToName(NPow3, args.c3))
outf = open(FileName, "w")

AccRate = 0 # Это количество принимаемых шагов в траектории, чтобы вычислить долю принятия (должна быть в диапазоне 20-60 %)

# начинаем итерации метода Метрополиса 
for nstep in range(0,args.NumSteps):
    # генерируем новую точку, приписывая случайное смещение к нынешнему положению в пространстве
    trialR = currentR + np.random.uniform(low=-args.MaxStep, high=args.MaxStep, size=3) 
    # считаем значение орбитали в этой точке
    trialOrbP = orb(r=trialR, n1=NPow1, n2=NPow2, n3=NPow3, coeff1=args.c1, coeff2=args.c2, coeff3=args.c3, r0 = args.R0)        
    # выбрасываем вероятность принятия новой точки
    Ptrial = np.random.uniform(low=0, high=1)
    
    # а здесь мы сохраним значение того, примем ли мы новую точку, или нет
    DoWeAccept = False
    
    # сначала просто проверим, что новая вероятность (квадрат орбитали) выше, чем была, и если да, то принимаем точку
    if (trialOrbP**2 > currentOrbP**2):
        DoWeAccept = True
    else:
        # если вероятность новой точки ниже, сравниваем вероятность перехода в эту точку с вероятностью принятия
        if trialOrbP**2/currentOrbP**2 > Ptrial:
            DoWeAccept = True
    
    # если новую точку принимаем, то она становится новым значенем точки в траектории, а ещё увеличиваем число принятых точек
    if DoWeAccept:
        currentR = trialR
        currentOrbP = trialOrbP
        AccRate += 1
        shift = np.zeros(currentR.shape) # в этом случае сдвиг никакой нам не нужен
    else:
        # если точку не приняли, чтобы было не очень уныло, сохраним значение старой точки с некоторым малым случайным сдвигом
        shift = np.random.uniform(low=-args.MaxSmallShift, high=args.MaxSmallShift, size=3)
    
    # и если часть игнорирования траектории закончилась, то сохраняем новое значение    
    if nstep > int(args.NumSteps * args.PartToIgnore):
        outf.write(" %15.10f %15.10f %15.10f " % tuple(currentR + shift))
        outf.write("  %15.5e   %10i\n" % (currentOrbP, nstep))    
        outf.flush()
    
    
# в конце выдаём процент принятых точек в траекторию (хотелось бы, чтобы оно было в районе 20-60 %)
print("Acc rate = %15.10f %%" % (100.*float(AccRate)/float(args.NumSteps)) )
outf.close()    


############## А теперь построим всю эту красоту, если юзер захотел
if args.plot:
    import matplotlib.pyplot as plt
    from mpl_toolkits.mplot3d import Axes3D
    
    fig = plt.figure()
    ax = fig.add_subplot(projection='3d')
    
    data = np.loadtxt(FileName)
    ax.scatter(data[:,0], data[:,1], data[:,2], c=data[:,3],cmap = 'coolwarm',s=args.MaxSmallShift*0.1)
    ax.set_xlabel('X')
    ax.set_ylabel('Y')
    ax.set_zlabel('Z')
    
    plt.show()

спасибо за внимание.

Ладно, шучу, здесь мы ещё раз немного пройдёмся по тому, что такое орбитали, какие они бывают, и как их строить с помощью вышеприведённого скрипта.

Как выглядят орбитали?

Атомная орбиталь -- это волновая функция для выбранного электрона в атоме, поэтому будем обозначать их буковкой ψ. Согласно квантовой механике, мы не можем знать где электрон находится и как быстро он куда-то летит, но нам доступно знание (например) о вероятности нахождения этого электрона в пространстве. И орбитали это знание нам и предоставляют: найти электрон в месте с координатой x (p(x)) даётся квадратом волновой функции: p(x)=|ψ(x)|2. Сами атомные орбитали можно представить в виде двух компонент: радиальной (R, зависящей только от того, как далеко от ядра убежал электрон) и угловой (A, зависящей только от того, с какой именно стороны от ядра находится наша частица), так что ψ=R·A.

Для наших целей визуализации мы вполне можем себе представить каждую орбиталь в виде:

\psi(x,y,z) = \underbrace{\exp\left(-\frac{\sqrt{x^2 + y^2 +z^2}}{R_0}\right)}_{R} \cdot \underbrace{x^{n_x} \cdot y^{n_y} \cdot z^{n_z}}_{A}

здесь радиальная часть дана как экспоненциально убывающая вероятность найти электрон вдали от ядра, где параметр R0 контролирует "размер" орбитали, а угловая часть дана как произведение координат в некоторых степенях n≥0. Собственно, тип орбитали, который даётся орбитальным квантовым числом l в данном представлении -- это просто сумма всех степеней для x,y,z координат:

l = n_x + n_y + n_z

Т.е. для s-орбиталей (l=0) нам нужны nx=ny=nz=0, для p-орбиталей, которых у нас три штуки, нам нужны следующие комбинации:

  • nx=1, ny=nz=0 (px-орбиталь),

  • ny=1, nx=nz=0 (py-орбиталь),

  • nz=1, nx=ny=0 (pz-орбиталь).

Но дальше всё будет плохо. Для каждого орбитального квантового числа l у нас должна быть N=2l+1 орбиталь, и для s и p у нас всё удовлетворяло этому соотношению. А вот дальше, из условия l=nx+ny+nz у нас будет получаться слишком много допустимых комбинаций. Например, для d-орбиталей (l=2) по формуле у нас должно быть 5 функций, но возможных комбинаций у нас будет уже 6 штук. Что делать с лишними?

Весь сыр-бор будет заключаться в том, что лишние орбитали -- это будут какие-то комбинации некоторых N=2l+1-избранных, настоящих орбиталей, которые то нас и интересуют. Поэтому, чтобы их построить, нужно будет несколько обобщить угловую часть волновой функции, взяв взвешенную сумму различных форм орбиталей:

A_\text{комб} = c_1 x^{n_{x1}} y^{n_{y1}} z^{n_{z1}} + c_2 x^{n_{x2}} y^{n_{y2}} z^{n_{z}} + c_3 x^{n_{x3}} y^{n_{y3}} z^{n_{z3}} + \ldots

где c -- это некие постоянные коэффициенты. И вот для окончательного изображения орбиталек мы и будем использовать выражение для волновой функции

\psi(x,y,z) = A_\text{комб} \cdot \overbrace{ \exp\left( -\frac{\sqrt{x^2 + y^2 +z^2}}{R_0} \right) }^{R}

В скрипте все эти степени n и коэффициенты c задаются различными аргументами (о чём можно узнать запустив скрипт с опциями -h или --help):

  --c1 C1               Коэффициент перед первой угловой функцией
  --c2 C2               Коэффициент перед второй угловой функцией
  --c3 C3               Коэффициент перед третьей угловой функцией
  --nx1 NX1             Степень n в функции x**n для первой угловой функции
  --nx2 NX2             Степень n в функции x**n для второй угловой функции
  --nx3 NX3             Степень n в функции x**n для третьей угловой функции
  --ny1 NY1             Степень n в функции y**n для первой угловой функции
  --ny2 NY2             Степень n в функции y**n для второй угловой функции
  --ny3 NY3             Степень n в функции y**n для третьей угловой функции
  --nz1 NZ1             Степень n в функции z**n для первой угловой функции
  --nz2 NZ2             Степень n в функции z**n для второй угловой функции
  --nz3 NZ3             Степень n в функции z**n для третьей угловой функции

С этими знаниями попробуем нарисовать простейшие типы орбиталек.

S-орбитали

Как многие могут помнить (из курса школьной химии) -- это такие "шарики", когда электрон летает вокруг атома в виде шарообразного облака. Наша волновая функция имеет вид c1=1, nx1=ny1=nz1=0. Чтобы построить эту орбитальку скриптом, данным в самом начале поста, надо будет выполнить команду,

python3 gen-plot_orb.py --plot

где gen-plot_orb.py -- это название скрипта, а "--plot" -- это опция, чтобы включить отрисовку полученной орбитали. В результате мы получим картинку, где число точек и их цвет будет отображать значение волновой функции:

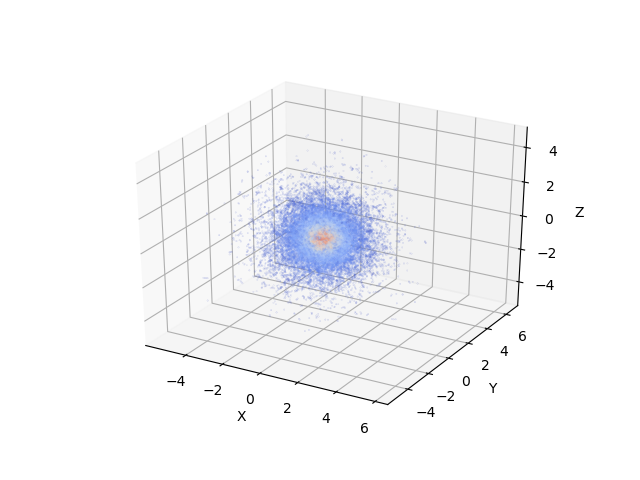
Изображение s-орбитали, полученное скриптом выше
Изображение s-орбитали, полученное скриптом выше

Я никакущий специалист по Matplotlib, поэтому отсюда и далее я буду приводить картинки, построенные при помощи Gnuplot косыми скриптами, типа того, что убран под спойлер.

Скрипт для Gnuplot
set view 82.,32.

set xlabel "x"
set xtics 0.,1e5,1e5


set ylabel "y"
set ytics 0.,1e5,1e5

set zlabel "z"
set ztics 0.,1e5,1e5

set cblabel "ψ"
set cbtics 0.,1e5,1e5

set xyplane at 0
set view equal xyz

unset key

set terminal pngcairo size 1000,1000 font "FreeMono,24"


##### s #################################
set title "s"
FNAME="orbital_+1.00s.dat"
set output "s.png"
maxWFN=0.9089320000
###########################################

set cbrange [-maxWFN:maxWFN]
splot FNAME u 1:2:3:4 w p pt 7 ps 0.1 lc palette

Соответственно, перестроенная Gnuplot-ом s-орбиталь будет выглядеть так:

s-орбиталь, построенная Gnuplot-ом.
s-орбиталь, построенная Gnuplot-ом.

Всё, как мы и привыкли, шарик.

P-орбитали

Здесь l=1, и, соответственно, три p-орбитали, мы можем построить командами:

python3 gen-plot_orb.py --nx1 1 --plot
python3 gen-plot_orb.py --ny1 1 --plot
python3 gen-plot_orb.py --nz1 1 --plot

В результате чего мы получим следующие изображения орбиталей:

Три p-орбитали.
Три p-орбитали.

Вновь, всё выглядит как и ожидалось после изучения школьной программы: три "гантельки", направленные в три разные стороны, и каждая половинка орбитали имеет знак, противоположный другой половинке той же гантели.

D-орбитали

l=3, и тут должно быть пять орбиталей. Три из них строятся просто (т.н. dxy, dxz, dyz):

python3 gen-plot_orb.py --nx1 1 --ny1 1 --plot
python3 gen-plot_orb.py --nx1 1 --nz1 1 --plot
python3 gen-plot_orb.py --ny1 1 --nz1 1 --plot

Выглядят они как две спаренные гантели p-орбиталей но с изменёнными знаками половинок, например:

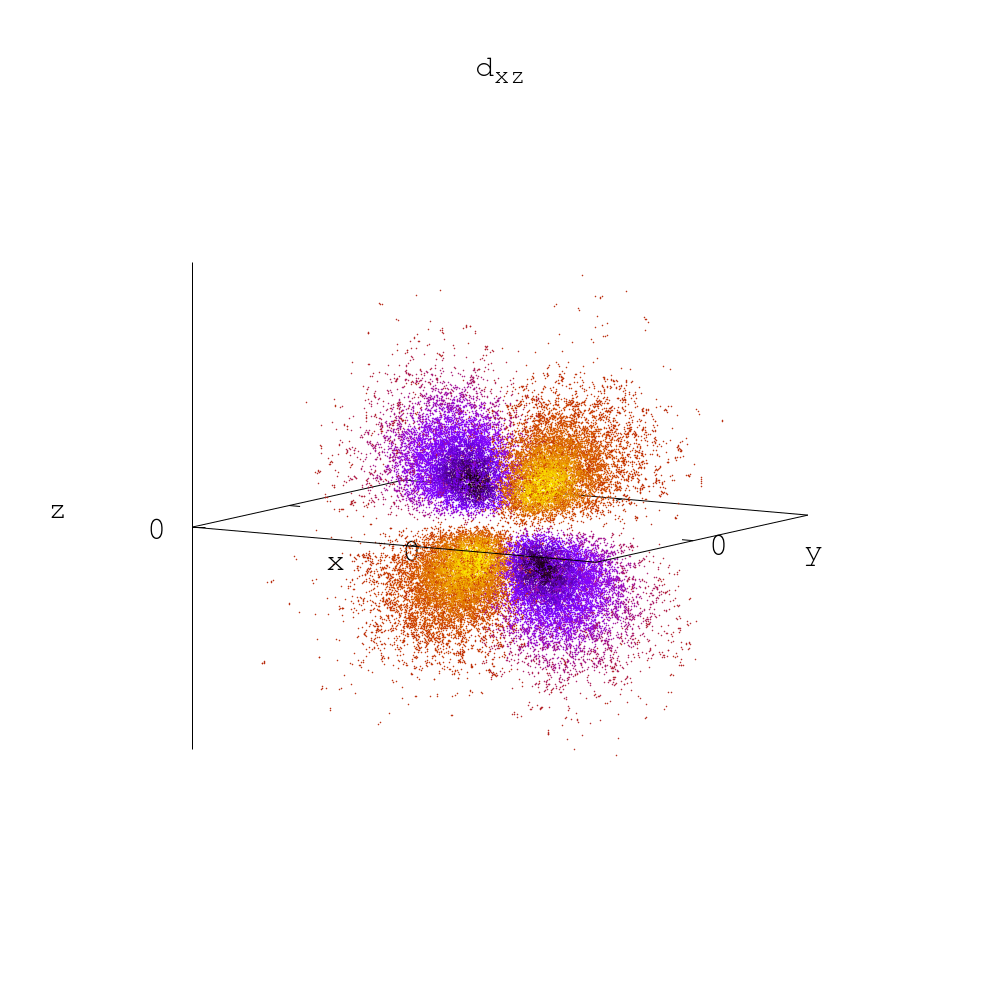
dxz-орбиталька
dxz-орбиталька

Ещё одна из таких спаренных гантелей получается как разность x2 и y2 орбиталей командой 

python3 gen-plot_orb.py --nx1 2 --ny2 2 --c1 1 --c2 -1 --plot

А вот последняя орбиталь, называемая d(z2) -- самая сложная, она на самом деле состоит из трёх наших орбиталей-кирпичиков. Коэффициенты между положительными и отрицательными кусками на самом деле можно найти, но это надо или копать литературу, или поднимать зубодробительный матан, так что я их просто подобрал, чтобы было похоже на то, как эта орбиталь должна выглядеть:

python3 gen-plot_orb.py --nz1 2 --nx2 2 --ny3 2 --c1 3 --c2 -1 --c3 -1 --plot

что даёт в результате искомую форму однозначной гантельки с надетым на неё бубликом тором:

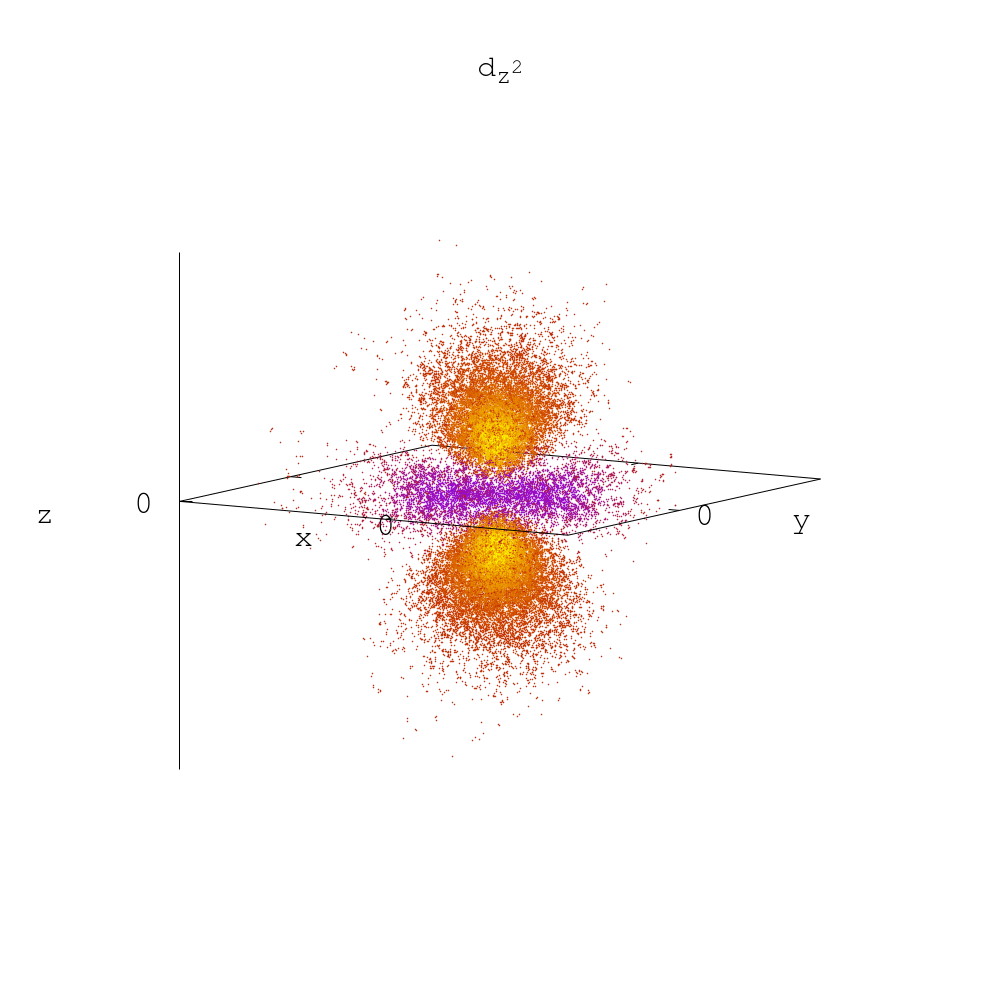
dz2-орбиталька
dz2-орбиталька

А более сложные виды орбиталей оставляю на самостоятельный разбор, ибо f-функций будет уже 7 штук, конструируемых из 10 простейших орбиталек.

Парочка дисклеймеров и альтернатив

Просто парочка комментариев, которые я не знаю куда запихать ещё.

  • На самом деле, радиальная часть атомных орбиталей имеет существенно более сложный вид, но для целей визуализации это не очень важно, и в тех же квантово-химических расчётах по методу МО ЛКАО (молекулярные орбитали как линейные комбинации атомных орбиталей) используются именно выражения, аналогичные тому, что использовали мы, так что сильно мы от такого упрощения не соврали.

  • Я понимаю, что мог уже достать всякими штуками типа орбиталек и Монте-Карло. Если это так, дайте знать в комментах (там можно как выразить своё "фи", так и добавить более конструктивных комментов, например, о чём бы хотелось видеть статьи).

  • Много кому не нравится этот стиль изображения орбиталей (достаточно посмотреть на отклики к посту https://habr.com/ru/post/548704/). Мне этот стиль, очевидно, нравится, поскольку он, как мне кажется, отражает статистическую природу волновой функции, а ещё в моём больном мозгу, видимо, он ассициируется с чем-то типа импрессионизма. Этот скрипт и картинки я делал для своей образовательной деятельности, так что могу только сказать "не нравится -- не ешьте".

  • В качестве простой (и бесплатной!) альтернативы, могу посоветовать молекулярный визуализатор Jmol (http://jmol.sourceforge.net/). Помимо кучи реально полезных в работе функций, он умеет и просто строить орбитали водородоподобного атома в стандартном виде. Например, орбитали можно построить из консоли парочкой команд (см. например здесь).

  • А ещё на YouTube есть классный ролик об изображении орбиталей в виде Бомовских траекторий: https://youtu.be/W2Xb2GFK2yc .

P.S.

Чтобы не быть голословным по поводу Jmol, вот изображение d-орбитальки, полученное командами ниже:

isosurface phase atomicOrbital 3 2 0
set axesMolecular;set axesScale 0.5;axes on
moveto 1.0 { 462 -868 -180 47.18} 141

Спасибо за внимание.

Комментарии (11)


  1. uoak
    12.09.2021 20:18
    #23475540
    +4

    >>А вот дальше, из условия l=nx+ny+nz у нас будет получаться слишком много допустимых >>комбинаций.

    казалось бы, вопрос "лишних" орбиталей можно решить, если вместо указания полиномов "руками" использовать сферические гармоники https://en.wikipedia.org/wiki/Spherical_harmonics
    которые кажется есть в scipy
    https://docs.scipy.org/doc/scipy/reference/generated/scipy.special.sph_harm.html

    Это я не к тому, чтобы обесценивать данную визуализацию (картинки красивые), просто кажется что значительно проще было бы указать скрипту 2 целых числа (полный момент L и его проекцию M=-L..L) вместо того чтобы мучаться с шестью коэффициентами в качестве входных параметров "-nz1 2 --nx2 2 --ny3 2 --c1 3 --c2 -1 --c3 -1"


    1. Moskus
      12.09.2021 22:43
      #23475874
      +1

      Это я не к тому, чтобы обесценивать данную визуализацию

      Где-то в обществе глубоко неправильно, если перед объективной критикой и предложением, как сделать лучше, приходится (или возникает ощущение, что приходится) делать такие вступления.


    1. madschumacher Автор
      12.09.2021 23:26
      #23475970

      Спасибо за комментарий.

      Да, это действительно можно делать. Там это концептуально чуточку посложнее, т.к. надо залезать в алгебру сферических гармоник, чтобы сделать для начала действительные комбинации (впрочем, там не сложно, надо брать комбинации с противоположными значениями магнитного квантового числа), а потом ещё избавиться от комплексных чисел, но в целом это вполне хорошая задачка: переделать код под такое.

      Собственно, нынешнее представление бралось ещё и из-за удобства построения различных демонстраций гибридизации, там это чуточку более визуально понятно, чем в терминах сферических гармоник.


  1. CrazyScientist
    12.09.2021 23:26
    #23475972

    По-моему надо количество точек увеличить, чтоб более заметна форма была в виде размытого облака. По факту классическая рисовка - это поверхность доверительной вероятности. Можете построить их для квартилей волновой функции, в дополнение к точкам.


    1. madschumacher Автор
      12.09.2021 23:33
      #23475994

      По факту классическая рисовка - это поверхность доверительной вероятности.

      Не совсем так: стандартная рисовка -- это изоповерхности для заданного значения вероятности (чисто из-за простоты).

      По факту классическая рисовка - это поверхность доверительной вероятности.

      А для этого есть в коде отдельный ключик: --NumSteps. Я на него не обращал внимания, т.к. концептуально он мало на что влияет, а форма в таком построении всегда на дальних рубежах будет "рваной".

      Можете построить их для квартилей волновой функции, в дополнение к точкам.

      Спасибо, но мне кажется это лишнее, чисто из-за того, что изображение в виде поверхности умеет хорошо строить тот же Jmol.


  1. flx0
    13.09.2021 12:32
    #23477580
    +3

    matplotlib очень тормозной с 3D-графиками. Я крайне рекомендую mayavi. Туда можно напихать намного больше точек, с прозрачностью, покрасом и всем остальным, и при этом его можно будет на приемлемой скорости вертеть, приближать и т.д. Интерфейс примерно такой же как в matplotlib, я только помнял


    ax.scatter(data[:,0], data[:,1], data[:,2], c=data[:,3],
    cmap = 'coolwarm',s=args.MaxSmallShift*0.1)

    на


    mlab.points3d(data[:,0], data[:,1], data[:,2], data[:,3],
    colormap='coolwarm', scale_factor=args.MaxSmallShift*0.2, scale_mode='none')

    и получилось вот это


    картинка

    image


    1. madschumacher Автор
      13.09.2021 16:04
      #23478562

      Спасибо большое, очень классная рекомендация.


  1. multibook
    13.09.2021 21:45
    #23479918

    А где на картинках ядро атома?


    1. QDeathNick
      13.09.2021 22:18
      #23480024
      +2

      В центре :)

      Оно слишком мало, чтобы отобразить в масштабе


  1. APrioriAPosteriori
    15.09.2021 22:20
    #23487886

    Ой визуалочка прямо для меня!

    Вопрос от дилетанта: не могли бы Вы на пальцах разъяснить, что такое R_0, которая "контролирует "размер" орбитали". Особенный конфуз вызывает "размер орбитали," можно для людей простых н(насколько это возможно) объяснить, как вообще определяется мера для размера орбитали, короче, что это такое и как замерить или определить размер орбитали?


    1. madschumacher Автор
      15.09.2021 22:23
      #23487892

      не могли бы Вы на пальцах разъяснить, что такое R_0, которая "контролирует "размер" орбитали".

      А очень просто. Например, мы можем посчитать размер орбитали как среднее значение радиуса полёта электрона (просто усреднить расстояние от ядра по соответствующему распределению). И вот эта величина и будет пропорциональна R_{0}.