31.07.2021 17:03
madschumacher 23 4700 Источник

В этой публикации мы попробуем подробно разобрать, что же такое сфера Блоха, иллюстрирующая пространство состояний одного двухуровневой квантовой системы, что в области квантовых вычислений зовётся "кубитом". Для тех, кто желает понять, зачем на математике мучают бесполезными комплексными числами, узреть одно из красивейших применений комплексных чисел и сферической системы координат.

Сфера Блоха
Сфера Блоха

Центральной идеей квантовых компьютеров является переход от использования кодировки информации в виде последовательности битов, которые могут принимать значения 0 и 1, к последовательностям кубитов. Каждый кубит -- это двухуровневая квантовая система далее мы будем использовать эти определения как эквивалентные понятия: у нас есть состояние |0⟩, являющееся аналогом 0 бита, и состояние |1⟩, аналог 1 бита. Вариантов того, что из себя могут представлять |0⟩ и |1⟩, очень много: спины |0⟩ = |↑⟩, |1⟩= |↓⟩ "вверх"/"вниз", состояния ангармонического осциллятора, поляризации фотонов (см. подробнее, например, здесь). Но в квантовой механике, согласно принципу суперпозиции, все подобные кубиты описываются при помощи волновой функции, вектора состояния |ψ⟩:

|\psi\rangle = c_0 |0\rangle + c_1 |1\rangle

Поскольку наша система по нашему же предположению, имеет только два возможных состояния для финального измерения, то получается, что состояние описывается двумерным вектором комплексных коэффициентов перед состояниями c0 и c1, т.е. (c0,c1)T, а наши состояния |0⟩ и |1⟩ являются базисными векторами, причём перпендикулярными друг другу, записывается это как

\begin{cases} \langle 0 | 0\rangle = \langle 1|1\rangle =1 \\ \langle 0 | 1\rangle = 0 \end{cases}

Но не всё так просто с этим выражением, по своему смыслу, коэффициенты c0 и c1 связаны с вероятностью обнаружить кубит в состоянии |0⟩ или |1⟩, обозначим их p0 и p1:

\begin{cases} p_0 = \frac{|c_0|^2}{|c_0|^2 + |c_1|^2} \\ p_1 = \frac{|c_1|^2}{|c_0|^2 + |c_1|^2} \end{cases}

Мы, конечно, можем позволить себе выбирать эти коэффициенты какими угодно, но физически значимыми являются т.н. нормированные коэффициенты, такие что

\langle \psi | \psi \rangle = |c_0|^2 + |c_1|^2 = 1

Т.е. полная вероятность найти систему в состоянии |ψ⟩ равна единице, в этом случае квадрат модуля каждого из коэффициентов -- это просто вероятность найти кубит в соответствующем базисном состоянии |n⟩ (pn=|cn|2, n=0,1). Выражение |c0|2+|c1|2=1 можно легко параметризовать при помощи основного тригонометрического тождества:

\overbrace{ \cos^2\left(\frac{\theta}{2}\right) }^{|c_0|^2} + \overbrace{\sin^2\left( \frac{\theta}{2} \right)}^{|c_1|^2} = 1

Любое комплексное число z=a+b·i можно представить в показательной форме:

z = a+b\cdot i = \underbrace{A}_{\sqrt{a^2 + b^2}} \cdot \exp(i\varphi)

где A=|z|≥0 -- это модуль комплексного числа, а φ -- фаза z, вычисляемая через преобразование в полярные координаты:

\begin{cases} a = A \cdot \cos(\varphi) \\ b= A \cdot \sin(\varphi) \end{cases} \Rightarrow \frac{b}{a} = \tan(\varphi)

Отсюда видно, что модули коэффициентов c0 и c1 должны быть неотрицательными. Исходя из основного тригонометрического тождества, мы можем определить коэффициенты волновой функции |ψ⟩ как

\begin{cases} |c_0| = \cos(\theta/2) \\ |c_1| = \sin(\theta/2) \end{cases}

При такой параметризации, из условия |cn|≥0, у нас получается, что угол θ может меняться от 0 до π, и мы выбираем это, осознанно, чтобы этот угол был похож на полярный азимутальный угол в сферических координатах, собственно, для этого и нужна двойка в θ/2. Но на самом деле для этого есть и более физические предпосылки

И, само, собой, используя показательную форму комплексных чисел, мы можем представить коэффициенты волновой функции в виде:

\begin{cases} c_0 = \cos(\theta/2) \cdot e^{i\varphi_0} \\ c_1 = \sin(\theta/2) \cdot e^{i\varphi_1} \end{cases}

Где по смыслу углы φn -- это полярные углы. Вроде всё хорошо, но у нас оказывается, что состояние |ψ⟩ определяют три числа: азимутальный угол (θ) и два полярных (φ0 и φ1). Но возникает резонный вопрос: а все ли они нужны, и ответ, как все уже догадались, нет.

В квантовой механике нас интересуют наблюдаемые величины, а представляются они в виде операторов, например, если у нас есть величина O от слова "observable", то её оператор обозначается добавлением сверху крышечки. В случае двухуровневой системы, оператор -- это по-сути, матрица, действующая на вектор коэффициентов (c0,c1)T, и превращающая его в вектор новых коэффициентов:

\hat{O} = \begin{pmatrix} \langle 0 | \hat{O} | 0\rangle & \langle 0|\hat{O} |1 \rangle \\ \langle 1|\hat{O}|0\rangle & \langle 1 | \hat{O} | 1 \rangle \end{pmatrix} = \begin{pmatrix} O_{00} & O_{01} \\ O_{10} & O_{11} \end{pmatrix}

где Onm=⟨n|O|m⟩ -- это обозначение соответствующих матричных элементов. Стоит заметить, что матрица оператора у нас эрмитова, т.е. ⟨0|O|1⟩=⟨1|O|0⟩* звёздочка в верхнем индексе обозначает комплексное сопряжение. Для нас важно, что среднее значение любой произвольной наблюдаемой для заданного состояния было бы одним и тем же числом, т.е. если

\langle \psi | \hat{O} | \psi \rangle = \langle \psi' | \hat{O} | \psi'\rangle

то мы разницы между состояниями |ψ⟩ и |ψ'⟩ не увидим: для нас они будут наблюдаемо одним и тем же состоянием. Теперь предположим, что |ψ'⟩=eiφ·|ψ⟩, тогда ⟨ψ'|=e-iφ·⟨ψ|, а значит

\langle \psi' | \hat{O} | \psi' \rangle = \exp(-i\varphi + i\varphi) \cdot \langle \psi | \hat{O} | \psi\rangle = \langle \psi| \hat{O} | \psi \rangle

т.е. фаза всего состояния даёт нам то же самое наблюдаемое состояние. Поэтому мы можем переписать наше двухуровневое состояние

|\psi\rangle = \cos(\theta/2) e^{i\varphi_0} |0\rangle + \sin(\theta/2) e^{i\varphi_1} |1\rangle

как

|\psi\rangle = e^{i\varphi_0} \cdot ( \cos(\theta/2) |0\rangle + \sin(\theta/2) e^{i(\varphi_1 - \varphi_0)} |1\rangle )

Соответственно, исходя из вышесказанного, можно спокойно проигнорить множитель eiφ0, и тогда единственным полярным углом, который у нас останется, будет разность фаз φ=φ1-φ0, и только сий угол определяет наше квантовое состояние.

В сухом остатке, наше состояние |ψ⟩ имеет вид:

|\psi\rangle = \cos\left(\frac{\theta}{2}\right) |0\rangle + e^{i\varphi} \cdot \sin\left(\frac{\theta}{2}\right) |1\rangle

и параметризуется двумя параметрами:

  • углом φ в интервале от 0 до 2π имеющим смысл разности фаз между двумя двумя базисными состояниями,

  • углом θ, от 0 до π, задающим относительное "содержание" базисных состояний |0⟩ и |1⟩ в нашей волновой функции |ψ⟩.

Но вся наша конструкция очень подозрительно напоминает сферические координаты, которые, традиционно, задаются следующим образом:

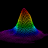
\begin{cases} x = r \cos(\varphi) \sin(\theta) \\ y = r \sin(\varphi) \sin(\theta) \\ z = r \cos(\theta) \end{cases}

где r -- радиус, φ -- полярный угол (от 0 до 2π), а θ -- азимутальный угол (от 0 до π). Если мы зафиксируем радиус, то изменение углов опишет нам сферу в трёхмерном пространстве, а поскольку углы определены точно так же, как и для нашей волновой функции для двухуровневой системы, то мы можем отобразить все возможные состояния, как точки на сфере фиксированного радиуса r, и такое представление состояний двухуровневой системы зовётся сферой Блоха, в честь Нобелевского лауреата по физике Феликса Блоха.

Разберёмся как эта сфера устроена см. рисунок в самом начале статьи, разобрав, какие вектора (x,y,z)T в трёхмерном пространстве соответствуют каким состояниям |ψ⟩.

  • При θ=0 (и любом значении φ) мы получим состояние |ψ⟩=|0⟩, это будет соответствовать вектору (0,0,r)T, это верхняя точка сферы, её "северный полюс".

  • Напротив "северного полюса" будет южный полюс (0,0,-r)T, при θ=π (и любом значении φ), это соответствует состоянию |ψ⟩=|1⟩. В этом смысле, наши базисные состояния -- это уникальные противоположности.

  • При θ=π/2 и каком-то значении φ, мы окажемся на экваторе (z=0, x2+y2=r2), когда в нашем состоянии |ψ⟩ ровно 50/50 вкладов от состояний |0⟩ и |1⟩.

  • Соответственно, в "северном полушарии" (выше экватора, при z>0) у нас будет больше |0⟩ в состоянии |ψ⟩, а в "южном полушарии" (ниже экватора, при z<0), наоборот, больше |1⟩.

Вот таким вот нехитрым способом можно легко и просто визуально изображать всякие весёлости, происходящие с состоянием двухуровневой системы. Конечно, физический смысл этого изображения существенно богаче: например, для частиц со спином 1/2 эта сфера будет давать пространственное направление спина, но это уже отдельный интересный вопрос.

UPDATE:

Спасибо за комментарии к статье, благодаря ним я вспомнил, что совсем забыл о важном куске: зачем в принципе нужен угол φ. Распишем, как выглядит для произвольного состояния |ψ⟩ среднее значение некоторой наблюдаемой O заданной оператором с матричными элементами :

\langle \psi | \hat{O} | \psi\rangle = |c_0|^2 \overbrace{ \langle 0|\hat{O}|0 \rangle }^{O_{00}} + 2 \mathrm{Re} (c_0^* c_1 \overbrace{\langle 0 | \hat{O}|1\rangle}^{O_{01}} ) + |c_1|^2 \overbrace{\langle 1|\hat{O}|1 \rangle}^{O_{11}}

Здесь мы использовали тот факт, что сумма комплексного числа z=a+i·b и его комплексно-сопряжённого числа z*=a-i·b равна удвоенной действительной части любого из них, т.е. z+z*=2·a=2·Re(z)). Если переписать это выражение в терминах полярного и азимутального угла сферы Блоха, мы получим

\langle \psi | \hat{O}|\psi \rangle = \cos^2\left(\frac{\theta}{2} \right) O_{00} + \sin(\theta) \mathrm{Re}(e^{i\varphi} O_{01}) + \sin^2\left(\frac{\theta}{2} \right) O_{11}

то есть значение каждой из наблюдаемых в явном виде зависит от обоих углов, поэтому ни один из них выкинуть из рассмотрения уже не получится. Как-то так.

Комментарии (23)


  1. Tyusha
    31.07.2021 18:11
    #23321038
    +1

    Да-а, группа SU(2) она такая. Мне нравится то, что 360 градусов не является в этом представлении тождественным преобразованием! У моих студентов обычно это вызывает ступор. :)


  1. da-nie
    31.07.2021 20:47
    #23321300

    О, квантмех. Может, вы меня просветите: меня вот занимает один вопрос. Если энергия фотона hv и не зависит от амплитуды ЭМ волны, а зависит только от частоты, то почему энергия ЭМ волны (вектор Умова-Пойтинга — плотность потока) зависит от амплитуды E и H волны.
    Как так получается? Я видел разбор этого вопроса в одной книжке. Там указано, что данную проблему снимает квантовая электродинамика. Но вот именно её я и не изучал. Не знаете ли вы ответа на этот вопрос («Мы хотим получить ответ простой и ясный» :) )? Но не 42. :)


    1. madschumacher Автор
      31.07.2021 20:55
      #23321330
      +1

      Может, вы меня просветите: меня вот занимает один вопрос. Если энергия фотона hv и не зависит от амплитуды ЭМ волны, а зависит только от частоты, то почему энергия ЭМ волны (вектор Умова-Пойтинга — плотность потока) зависит от амплитуды E и H волны.

      Всё очень просто: для монохроматической волны с частотой v, амплитуда ЭМ поля пропорциональна числу фотонов. Детали там более забавные, но суть такая.


      1. da-nie
        31.07.2021 21:08
        #23321356

        амплитуда ЭМ поля пропорциональна числу фотонов.


        Да вроде как так просто это не решается.


        1. madschumacher Автор
          31.07.2021 23:05
          #23321564
          +1

          Не понимаю к чему приведенный фрагмент, что Вы хотели этим сказать?

          Но да, Вы правы, там всё непросто. Там нужно сначала написать гамильтониан свободного поля, произвести его вторичное квантование, и уже в конце получить факт, что оператор амплитуды, например, электрического, поля пропорционален сумме операторов рождения/уничтожения фотонов, что приводит к тому, что среднее значение квадрата амплитуды поля пропорционально числу фотонов.


          1. Tyusha
            31.07.2021 23:57
            #23321658
            +1

            Когда-то давно в студенчестве меня мучал один вопрос. Допустим, мы взяли поле, разложили на моды, получили операторы рождения-уничтожения этих мод. Но ведь разложение по модам можно взять какое угодно. Можно взять плоские волны, а можно по бесселям и сферическим полиномам разложить или как-то ещё, поэтому операторы вторичного квантования у нас будут разные, т.к. относятся к разным базисам разложения поля.

            Так вот, допустим мы зарегистрировали фотон детектором и знаем его энергию. А что это была за мода, которую мы поймали? Фотон, он вообще не в курсе, что мы тут поле раскладываем по системе функций.


            1. madschumacher Автор
              01.08.2021 10:33
              #23322342

              Так вот, допустим мы зарегистрировали фотон детектором и знаем его энергию. А что это была за мода, которую мы поймали? Фотон, он вообще не в курсе, что мы тут поле раскладываем по системе функций.

              Я тут сам могу наломать дров, но по ощущению (и без долгих размышлений), кажется, что надо копать сюда: один зарегистрированный фотон (без априорного знания его состояния) -- это не очень полезное измерение, т.к. тут выдирается один маленький кусочек состояния при помощи проекционного постулата.

              Тут надо или взять кучу этих систем в одном и том же состоянии, облепить её детекторами во всех направлениях, и тогда удастся что-то установить об изначальном состоянии этого фотона, и кучи его собратьев, или иметь какое-то априорное знание о начальном состоянии, чтобы знать, куда и как ставить детекторы.


              1. Tyusha
                01.08.2021 15:02
                #23322916

                Мой ответ такой. Это зависит от физики детектора и от конкретных условий регистрации: сохранения квантовых чисел, типа момента, неопределённости импульса и координаты детектирования. При этом из поля "изымается" соответствующий такому набору условий пакет.

                Для каждого такого процесса существует некое представление гамильтонина поля, априорно неизвестное, где процесс поглощения будет выражаться изменением чисел заполнения в чистом виде с изменением на единицу. Но в других привычных нам гамильтонианах, например с использованием разложения по плоским волнам, данный процесс собственным отнюдь не будет.

                UPD: Стоит заметить, что при поглощении нашим детектором фотона типа наивной бесконечной плоской волны из ЭМ поля изымается мода в том числе где-то в галактике Андромеда.


                1. Tyusha
                  01.08.2021 15:26
                  #23323006

                  Я тут сама набросила на вентилятор про Андромеду, сама и отвечу.

                  Пускай действительно мы располагаем детектором совершенно монохроматичных фотонов – плоских волн. До тех пор, пока мы у себе этот фотон не зарегистрировали, ни мы, ни в Андромеде никто не может сказать, а присутствует такая мода в конфигурации поля.

                  После регистрации мы можем заявить: "Ой, смотрите-ка, оказывается и у нас, и вас там в Андромеде, вот такая мода была... но, извиняйте, уже нету, мы её сломали". Но могло случиться, что не мы поймали бы этот фотон, а на Андромеде причём в это же время(!). И тогда бы они слали нам миллионы лет сообщение с извинениями за порчу фотона и известием, что оказывается, и в наших, земных, окрестностях такая мода тоже присутствовала. Этот фотон одновременно везде и ничей. Кто поймал, тот и молодец. Если подумать, то парадокса тут нет.

                  Но ещё раз напомню об огромном допущении, что мы умеем ловить бесконечноплоские фотоны.


          1. da-nie
            01.08.2021 08:51
            #23322164
            -1

            Там просто перечислены вопросы, возникающие если так считать. И указание на их разрешение в теории поля.

            среднее значение квадрата амплитуды поля пропорционально числу фотонов.


            А тогда получается интересно. Среднее значение. Не точно равна, а среднее. Поле само-то квантуется? Или оно непрерывное? Если квантуется, то среднее значение тоже квантуется?


            1. madschumacher Автор
              01.08.2021 10:40
              #23322358

              Поле само-то квантуется? Или оно непрерывное?

              Поскольку электродинамика, которая описывает всё это дело, квантовая, то, естественно, поле тоже квантуется. Но при обычных интенсивностях полей, эффекты от квантования не заметны, поэтому в обычной жизни можно об этом не думать, и считать поле непрерывным, и описываемым классической электродинамикой.


        1. Tyusha
          31.07.2021 23:45
          #23321640
          +3

          Это очень очень плохой текст. Не знаю, что за книжка, но выбросите её, возьмите нормальную. Автор навязывает совершенно неправильные понятийные вопросы, которые сбивают с толку. Впечатление, что он сам недостаточно понимает квантовую механику.

          UPD: Нашла. Это "Курс физики" Геворкян Р.Г., Высшая школа, 1979

          В аннотации: "Предназначается для студентов вузов, в основном для вечерних и заочных отделений." Оно и видно.


          1. Stronczzz
            01.08.2021 07:37
            #23322076

            А какая книжка хорошая, чтоб без излишнего формализма, но с объяснением сути процессов?


            1. Tyusha
              01.08.2021 11:28
              #23322446
              +1

              Ожидала такой вопрос. Не знаю. К сожалению, возможно, лучше накачаться терфизным формализмом сначала, и там в конце откроется понимание. Как говорит, Райгородский, произойдёт катарсис. У меня нет рецепта, как хорошо понять кванты без математики.

              Во всех книжках по квантовой механике мне не нравится объяснение с самого начала, когда говорят про волновую функцию (ВФ), как о волне, как о некой распределённой плотности в пространстве. Да это так, но лишь отчасти, и нужно для того, чтобы хоть как-то начать изучать квантовую физику.

              Правда в том, что нет никакой ВФ. У меня долго тоже был вопрос, ну хорошо, ВФ — волна, а что колеблется-то? Сейчас моим ответом будет: а ничего не колеблется. ВФ в виде каких-то волн в пространстве — это всего лишь одно из ПРЕДСТАВЛЕНИЙ (в терминах теории групп) квантового состояния.

              Нет никакой ВФ в наивном понимании. Есть ВЕКТОР СОСТОЯНИЯ в абстрактном гильбертовом пространстве, которое к нашему физическому пространству не имеет никакого отношения.

              Не буду продолжать. Смысл в том, что глубина понимания приходит через математический аппарат. Но т.к. на таком продвинутом языке объяснить школьникам и первокурсникам никак не получится, вот мы и рассказываем про дуализм "частица-волна" (тьфу на него) про облака плотности вероятности...


            1. qbertych
              01.08.2021 14:53
              #23322892
              +1

              Попробуйте «Как понимать квантовую механику» Иванова. Он весьма крут, хотя будучи его студентом я за ним с трудом поспевал ;)

              А лучше всего взять конкретную задачу — скажем, квантовые вычисления, или какие-нибудь двущелевые эксперименты, или атомные часы/ЯМР/ЭПР/томографию — и разобраться с ней. Лучше по совету Tyusha начать с математики (она простая, максимум линейная алгебра для 1 курса), а потом уже осознавать, как оно работает.

              И главное: не надо лезть в интерпретации квантмеха без минимального бэкграунда, будет только хуже.


  1. freestlr
    01.08.2021 16:53
    #23323294

    Добрый день. Спасибо за статью, очень легко читается, не смотря на сложность темы.

    Но мне непонятен один вопрос. Для чего нужен угол φ? В выводе у вас все состояния зависят только от угла θ, а φ нужен только для того, чтобы поместить результат на поверхность сферы. Почему тогда нельзя обойтись просто углом θ на окружности?


    1. madschumacher Автор
      01.08.2021 17:12
      #23323350

      Спасибо большое за вопрос: это очень важный аспект, который у меня вылетел из головы во время написания статьи. Я проапдейтил текст, добавив нужное пояснение в конец.

      Спасибо ещё раз большое.


  1. plus79501445397
    03.08.2021 07:43
    #23329668

    Я бы еще упомянул о современных попытках преодолеть некоторые ограничения сферы Блоха, например о qsphere, используемой в квантовых вычислениях для визуализации многокубитного состояния.


    1. madschumacher Автор
      03.08.2021 07:59
      #23329698
      +1

      Это же попытка визуализации

      \mathbb{R}^N \rightarrow \mathbb{R}^3, \ N >3

      на мой взгляд все такие попытки: а) мало читаемые и чересчур сложные (всякие одномерные срезы или столбиковые диаграммы тут будут приятнее, на мой вкус), b) имеют различные ограничения, c) на порядок более сложные конструктивно.


    1. qbertych
      03.08.2021 21:22
      #23332692
      +1

      Это слишком сложно и почти бесполезно. Такие вещи гораздо лучше описываются при помощи Wigner function или Husimi Q-representation, и то не всегда.


      1. madschumacher Автор
        05.08.2021 19:57
        #23341018

        А как там поможет вигнеровская функция? Она же определена для x-p фазового пространства, а в многокубитных случаях обычно просто прямое произведение конечномерных пространств одночастичных состояний?


        1. qbertych
          05.08.2021 20:40
          #23341142

          Там фишка в разложении матрицы плотности системы по сферическим гармоникам, что позволяет представить состояние на обобщенной сфере Блоха (то есть сфере для N частиц). Поверхность этой сферы — это уже не Гильбертово, а фазовое пространство, и функция Вигнера там вполне применима.

          Это хорошо работает не только для простой запутанности типа сжатых состояний, но и для GHZ, Dicke states и прочих хардовых вещей. Началось все кажется с этой статьи, ну и сейчас встречается очень часто (например).


          1. madschumacher Автор
            07.08.2021 23:24
            #23347514

            Прикольно, спасибо большое.