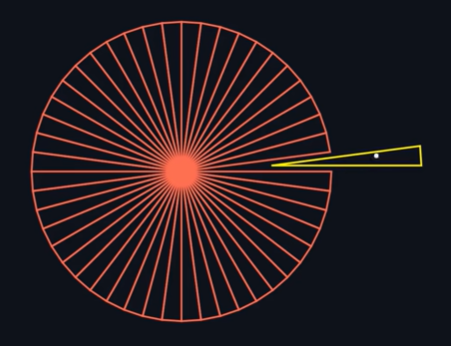
Допустим, вам нужно найти случайную точку с равномерным распределением в круге. Как же это сделать лучше всего? Когда я впервые начал изучать эту задачу, я работал над программным проектом, требовавшим случайного распределения значений в круге, но довольно быстро я спустился в неожиданно глубокую кроличью нору, заполненную любопытной математикой, поэтому решил объединить все свои находки в одну статью.
Прежде чем переходить к кругу, давайте упростим задачу и выберем случайную точку внутри квадрата. Для этого достаточно выбрать случайные координаты
Способ вполне рабочий, но мне не совсем нравится то, что этот алгоритм иногда приходится исполнять множество раз. Предположим ради простоты, что радиус нашей окружности равен
Давайте реализуем алгоритм на Python.
def rejection_sampling():
while True:
x = random() * 2 - 1
y = random() * 2 - 1
if x * x + y * y < 1:
return x, yЕсли я выполню эту функцию красивое количество раз (

На этом можно было бы и остановиться, но мы можем сделать так, чтобы подходящая точка гарантированно выбиралась с первого раза. Проблема в том, что мы используем неправильную систему координат (декартову), которая ограничивает нас, заставляя выбирать два значения, представляющие собой расстояния на перпендикулярных осях, которые мы называем
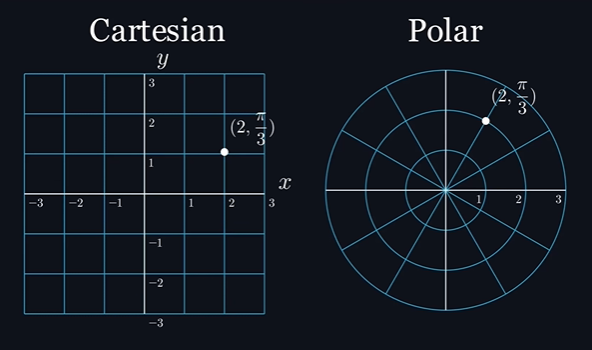
Достаточно взглянуть на графическое представление этих систем координат, чтобы понять, почему полярная система координат больше подходит для работы с кругами. Итак, всё, что нам нужно сделать — выбрать случайный радиус

Реализация этого алгоритма на Python содержит случайную переменную
def random_polar():
theta = random() * 2 * pi
r = random()
return r * cos(theta), r * sin(theta)Если мы снова выполним этот алгоритм 3141 раз, результаты должны выглядеть похожими на алгоритм выборки с отклонением… но это не так.

Как видите, точки гораздо плотнее располагаются в центре круга. Давайте разберёмся, почему. Мы знаем, что проблема не в генерировании

Мы можем описать процесс выбора радиуса или значения

Итак, мы знаем, что эта PDF нам не подходит. Давайте выясним, как она должна выглядеть для того, чтобы точки были равномерно распределены в круге. Так как длина окружности линейно зависит от радиуса, для сохранения одинаковой плотности точек их количество должно тоже линейно зависеть от радиуса. Следовательно, наша PDF должна быть линейной функцией, которую мы обозначим как

Любопытно то, что каждая PDF имеет интеграл

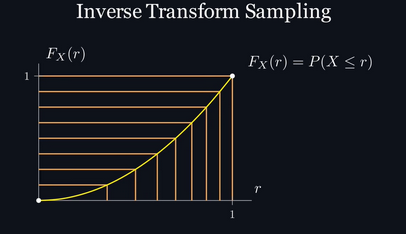
При помощи этой CDF мы можем воспользоваться стратегией под названием «метод обратного преобразования» (inverse transform sampling): берётся равномерное распределение, например, распределение нашего генератора случайных чисел, и преобразуется так, что хотя наша случайная переменная x не будет иметь равномерного распределения, сами вероятности, отложенные на оси y, будут им обладать. Давайте посмотрим, что произойдёт, если мы возьмём эти вероятности в качестве аргумента функции, по сути получив функцию, обратную нашей CDF. Если мы возьмём какое-то число из равномерно расположенных значений
Такое понимание уже достаточно ценно, но я покажу вам более строгое доказательство того, что подстановка случайной переменной с равномерным распределением в функцию, обратную нашей CDF, даст нужное нам распределение. Пока мы знаем, что CDF обозначает вероятность того, что случайная переменная

def sqrt_dist():
theta = random * 2 * pi
r = sqrt(random())
return r * cos(theta), r * sin(theta)Единственное отличие между этой и предыдущей функциями заключается в том, что для вычисления

Итак, теперь у нас есть два приемлемых способа выбора случайной точки с равномерным распределением внутри круга, но давайте не будем останавливаться. Существует и ещё один очень любопытный способ, приводящий точно к такому же результату.
Круг можно рассматривать как набор бесконечного множества бесконечно узких равнобедренных треугольников, повёрнутых относительно точки. Поэтому мы можем выбрать случайный треугольник, а затем выбрать в этом треугольнике случайную точку, чтобы получить случайную точку с равномерным распределением в круге.

Давайте вернёмся к тому, как мы выбирали случайную точку в квадрате — этот способ можно применить и к параллелограммам. Так как мы имеем дело с равнобедренными треугольниками, воспользуемся ромбом, который, как известно, состоит из двух равнобедренных треугольников, соединённых основаниями. Просто выберем случайную точку на двух соседних сторонах, а затем из каждой точки проведём линию, параллельную соседней стороне, и найдём точку их пересечения. Чтобы ограничить интервал только треугольником, мы можем провести диагональ и отражать все точки, попавшие не в ту часть ромба. Давайте обозначим четыре вершины ромба как

Теперь мы при необходимости сможем отразить точку относительно диагонали, которая находится посередине между точками

Всё это уже можно преобразовать в код на Python. Во-первых,
def sum_dist():
theta = random() * 2 * pi
r = random() + random()
if r >= 1:
r = 2 - r;
return r * cos(theta), r * sin(theta)Мы снова выполним алгоритм 3141 раз и получим равномерное распределение точек по кругу.
Однако у меня возник вопрос: почему сложение двух случайных величин не равно умножению одной случайной переменной на два? Проще всего рассуждать над этим вопросом на примере игровых костей. Если мы возьмём результат броска одной честной кости и умножим его на два, то увидим, что возвращаются только чётные числа и что кость имеет равномерное распределение. Однако если сложить результаты двух честных костей, то можно увидеть, что вероятность результата

Если мы представим, что отражаем правую половину графика, результат будет выглядеть очень похожим на желаемую PDF, но на этом я заметил кое-что странное. Оба этих способа вычисляют
К счастью, уже существует распределение Ирвина-Холла, сообщающее нам распределение суммы

Можно использовать их, но на самом деле это необязательно, потому что существует очень изящный геометрический вывод, хорошо работающий с низкими значениями

Но нужно помнить о том, что любое значение

Но зачем останавливаться на этом? Любая функция, имеющая такое распределение, теоретически должна выбирать значение
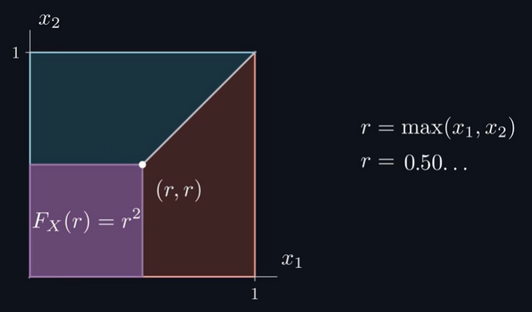
Я покажу вам ещё один способ, но призываю вас попробовать найти собственный, поскольку я перечислил далеко не все варианты. В этом последнем способе выбор значения
def max_dist():
theta = random() * 2 * pi
r = random()
x = random()
if x > r:
r = x
return r * cos(theta), r * sin(theta)Мы снова равномерно распределим 3141 точку в круге, но это нужно доказать. Доказательство выполняется схожим с распределением Ирвина-Холла способом — откладыванием величин
После разбора этих четырёх способов нам осталось протестировать их, чтобы узнать, какой выполняется быстрее всего. Выполнив каждую функцию 3 142 592 раза, мы получили такие значения времени:

По увеличению скорости выполнения: первый способ (rejection_sampling), четвёртый (max_dist), второй (sqrt_dist) и третий (sum_dist)
Значительно быстрее остальных оказалась выборка с отклонением (rejection sampling), и это логично, потому что остальные три способа содержат дополнительные затраты на выполнение операций синуса и косинуса. Значит ли это, что бОльшая часть нашей работы была проделана напрасно и что нам нужно было остановиться раньше? Я так не считаю, потому что если бы не эта задача, мне никогда бы не довелось познакомиться с PDF и CDF, да и с целым множеством интересных геометрических доказательств.
Комментарии (40)

FreeNickname
29.10.2021 09:45+6Выполнив каждую функцию 3 142 592 раза
Мне кажется, там должно быть 3 141 592 :) Интересная статья, спасибо!

mobi
29.10.2021 09:47+3Еще бы замеры скорости привести, потому что у меня есть стойкое ощущение, что для быстрого генератора случайных чисел (как правило, это вихрь Мерсенна) будет быстрее отбросить "неправильную" пару случайных чисел, чем рассчитывать значения синуса и косинуса.

osmanpasha
29.10.2021 11:39+4Дак они же приведены в самом конце. Правда, судя по всему, на чистом питоне, что несколько снижает ценность такого замера.

iroln
29.10.2021 21:41+1Да, в Python для подобных задач надо использовать numpy. Тогда и миллионы точек будут вычисляться за миллисекунды.
def sqrt_dist(n): theta = np.random.rand(n) * 2 * np.pi r = np.sqrt(np.random.rand(n)) return r * np.cos(theta), r * np.sin(theta) %timeit x, y = sqrt_dist(3141592) 139 ms ± 9.76 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
squaremirrow
30.10.2021 18:30+2Можно ускорить еще почти в два раза, просто поставив декоратор numba.njit:
import numpy as np from numba import njit def sqrt_dist(n): theta = np.random.rand(n) * 2 * np.pi r = np.sqrt(np.random.rand(n)) return r * np.cos(theta), r * np.sin(theta) @njit def sqrt_dist_nb(n): theta = np.random.rand(n) * 2 * np.pi r = np.sqrt(np.random.rand(n)) return r * np.cos(theta), r * np.sin(theta) %timeit x, y = sqrt_dist(3141592) 170 ms ± 1.21 ms per loop (mean ± std. dev. of 7 runs, 10 loops each) %timeit x, y = sqrt_dist_nb(3141592) 91.4 ms ± 715 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)

Goodwinnew
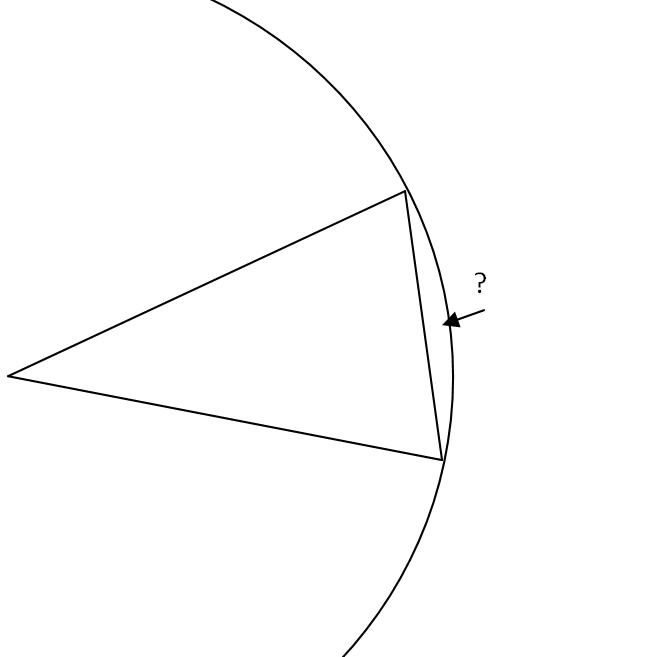
29.10.2021 09:48Только участок BD в треугольнике на самом деле является частью окружности.
Т.е. в данном алгоритме существуют области (предельно малые - но они есть), где точек принципиально не будет.
Я правильно понимаю?

Tiriet
29.10.2021 09:58+2мне тоже так померещилось сначала. но выбрав треугольник безконечно узким мы эту проблему в пределе полностью устраним.

Goodwinnew
29.10.2021 11:13-2IMHO - численными методами проблему полностью не устраним. "В пределе" - это математика.
А тут уменьшая "толщину" треугольников мы увеличиваем покрытие круга - но не 100%, всегда будут существовать зоны, свободные от точек. Да - это будет вида 0,00001% от общей площади - но будет.
Это как с интегралами. Площадь под кривой 3Х^2 от 1 до 2. Интеграл - легко видеть Х^3 и точное решение 8-1=7
А численными методами (суммируем площади прямоугольников под кривой) мы получим или 6,999999 или 7,000001 (смотря какие прямоугольники). Уменьшая толщину - мы повышаем точность = но точно 7 мы не получим.
PS
причем заданная точность вычислений (численные методы) будет работать в случае интеграла = нам нужна например точность 0,001%. уменьшаем толщину прямоугольников, пока разность между двумя вычислениями не составит требуемую величину.
а в случае случайного распределения точек мы не знаем исходной задачи, насколько критично наличие областей, в которых точек не будет вообще.

Tiriet
29.10.2021 11:33+3мы сначала переходим к пределу и получаем абсолютно точную (не на 0,0001%, а строго!) формулу для получения случайной равномерно-распределенной координаты точки внутри круга, а потом уже по этой точной формуле строим свои точки.

wataru
29.10.2021 14:08+4Да нет, там же математически показывается, что распределение у формулы точно такое же, как у предыдущей (с подстановкой в обратную CDF). Треугольник лишь нужен, чтобы додуматься до такой формулы.

AVI-crak
29.10.2021 10:23-2Заполнить квадрат, обрезать лишнее до круга.

FreeNickname
29.10.2021 12:16Так это тот же самый метод с отсечением (отбрасыванием), только вы шаг отсечения переносите в конец для всех точек. Плюс, сложнее понять, что мы закончили. Допустим, нам надо сгенерировать строго 100 точек внутри круга. Как мы поймём, что мы это сделали? Мы же не знаем, сколько из них в пределах круга, а сколько за пределами, пока не "обрежем".

vesper-bot
29.10.2021 10:46Неплохо, для студента второго курса, изучающего тервер. Для продакшн имеет смысл использовать оба способа — вначале приближение целевой фигуры примитивом, для которого "легко" построить функцию равномерного распределения, затем проверка на попадание точки в фигуру.

Tiriet
29.10.2021 11:59а зачем нужен примитив?
проверка попадания x*x+y*y < R^2- в худшем случае- три умножения, сложение и сравнение.
примитив- определение сектора, в котором используем примитив (два сравнения- по xy), определение координаты внутри примитива, отображение на круг и снова проверка попадания с теми же накладными расходами. в чем профит? Если мне надо простой читаемый код, вызываемый сто раз в секунду- то используем равномерный квадрат с отбрасыванием- все просто и понятно, а если надо миллиарды раз в секунду такие точки строить- то я бы тогда больше не за отбрасывание переживал, а за синусы и косинусы- (или любые другие трансцендентные функции)- и снова вернулся бы к отбрасыванию- пересчитать рандом каждые 3 из 10 случаев быстрее и проще, чем два синуса в каждом случае.

vesper-bot
29.10.2021 13:40+1Не в этой задаче, тут и так примитивом является или квадрат, или круг, и собственно вся статья посвящена способам сгенерировать равномерное распределение для примитива "круг". Я о более сложных задачах, где дана фигура неопределенной формы, но со списком условий на проверку принадлежности точки фигуре, и в ней нужно сделать равномерное распределение.

MuKPo6
29.10.2021 12:46Забавно. Ровно эту же задачу я решал, делая для игры Arma 3 скрипт бомбардировки участка в определенном радиусе. Выбирал именно второй метод с полярными координатами. Помню, что заметил странную "равномерность" в распределения бомб, но списал это на "показалось".

zamboga
30.10.2021 22:55Иными словами, до выпуска следующего релиза, бомбы (или повреждения от них) точнее, чем должны были бы быть, и игровой баланс слегка нарушен. Кто-то в реале заметил это, интересно?

v-oz
10.11.2021 14:07из бомбера? да там бы от истребителей уйти, а не статистику собрать для вычисления распределения :)

janatem
29.10.2021 12:56+1Скорости выполнения получились примерно одинаковы, потому что весь пар уходит в вычисление тригонометрических функций. Стоит побороться за то, чтобы от них избавиться.
Навскидку вижу такой способ, который, правда, требует вычисления квадратного корня, что гораздо дешевле синуса, но тоже дороговато. Рассмотрим, как распределено значение координаты x. Ее плотность должна быть пропорциональнa длине хорды, которая образуется прямой, заданной уравнением x=const. То есть нужно вычислять отображение sqrt(1-x^2). Осталось найти распределение координаты y при заданном значении x: оно будет распределено равномерно по всей длине хорды. И нужен еще один вызов квадратного корня для нахождения длины хорды.

5oclock
29.10.2021 13:34+1вместо того, чтобы преобразовать некое распределение, мы просто отклоняем все результаты, находящиеся вне нужного нам интервала.
Я не специалист, поэтому мне не очевидно: а характер распределения (в данном случае — равномерного) после отбрасывания части результатов — сохраняется?
vesper-bot
29.10.2021 13:41Для равномерного распределения это как раз верно. Но неверно в общем случае, но там и распределения в среднем имеют бесконечные хвосты.

Sayonji
30.10.2021 04:18Будет чуть более очевидно, если представить, что мы сперва накидываем много точек на квадрат, а потом лишние убираем, и обратить внимание, что результат по сути тот же.
Если же хочется унылое доказательство, то можно считать вероятность попасть в элемент площади х. Это будет вероятность сразу попасть в него, плюс вероятность попасть в молоко и следом в х, плюс вероятность дважды в молоко и следом в х... Прогрессию складываем, выходит х нормированное на площадь круга.
Если хочется нормальное доказательство, то выйдет равномерно в силу симметрии: попадание в молоко не влияет на то, куда полетит следующая точка. Другими словами, в параграфе выше ответ зависит от площади х, но не зависит от того, где эта площадь.

iShrimp
29.10.2021 19:24+2Если помнить, что суммирование двух случайных величин эквивалентно свёртке их PDF, то код можно сделать ещё проще:
def sum_dist(): theta = random() * pi r = random() - random() return r * cos(theta), r * sin(theta)— так как вычисление random() - random () даёт случайную величину с треугольным распределением, симметричным относительно 0.

pprometey
30.10.2021 12:28Мне на ум сразу пришло одно наиболее востребованное применение - онлайн казино, рулетка)

CImanov
30.10.2021 16:37Есть еще такой вариант, не проверял на скорость но по моему он может быть даже быстрее чем Rejection sampling. Не знаю как назвать этот вариант, она просто изменяет область значений y основываясь на значении x.
def nosin_dist(n): x = random() * 2 - 1; y = (random() * 2 - 1)*sqrt(1 - x^2); return x, y;
mobi
30.10.2021 16:43+1Такой способ не даст равномерное распределение, плотность в окрестности точек (-1,0) и (1,0) будет заметно выше.

wataru
30.10.2021 17:58Тут та же проблема что и в наивном методе в полярных координатах — не равномерное распределение.

Tarakanator
08.11.2021 14:53Значительно быстрее остальных оказалась выборка с отклонением (rejection sampling)
Не совсем так. В среднем, да.
А если считать для систем реального времени, то мы должны закладывать самую долгий вариант расчёта. А он тут бесконечность.



Tiriet
Подход с треугольниками неаккуратный- он дает распределение, очень близкое к случайному, но отличающееся от него в самой близи от границы круга. дело в том, что Ваш узкий треугольник- это все-таки треугольник, и между его основанием и окружностью есть небольшой участок, в котором точка уже за треугольником, но еще внутри круга. Как следствие- такие точки чуть-чуть отличаются по вероятности возникновения от "нормальных". На практике при малых тетах и небольших выборках это невозможно отследить, но для моделирования чего-нибудь методом Монте-Карло- вполне может дать заметные чудеса.
mobi
Там треугольник приводится только для объяснения окончательной формулы, и из текста программы видно, что зависимость от угла будет равномерной.
Tiriet
а, точно, недопонял.