Сумма целых чисел — что может быть проще? Сумма есть в SQL, в Java Stream API… в крайнем случае напишем сами. Как и всякая абстракция, она расходится с реальностью.
Вот счёт клиента в банке, по нему движения — положительные пополнения и отрицательные списания — в сумме дают текущий баланс. Так сумма работает в идеальном мире. А в реальности при большом минусе банк с отсрочкой, но предпримет нетривиальные действия вплоть до обращения в суд, чтобы закрыть финансовую брешь.
static long usualSum(LongStream changes) {
return changes.reduce(0, (a, b) -> a + b);
}Для склада вроде бы те же положительные приходы и отрицательные отгрузки в сумме дают текущий остаток. Но действия по увязке абстракции с реальностью придётся предпринимать безотлагательно — нельзя отгрузить товар, которого физически нет, нужно сразу считать неотрицательную сумму, поправляя отгрузку. Это касается всех материально-физических объектов — хоть наличных в кошельке, хоть овец в стаде.
static long nonNegativeSum(LongStream changes) {
return changes.reduce(0, (a, b) -> Math.max(0, a + b));
}А здесь уже проблемы реализации:
Неассоциативная бинарная операция нарушает контракт свёртки
Stream.reduce(). При вычислении послеStream.parallel()результат будет некорректным, отличным от результата последовательного вычисления.Внутри
Math.max()есть ветвление и заранее неизвестно, хватит ли остатка на складе для отгрузки. Как разбить вычисление на независимые куски для параллельных вычислителей, если следующий кусок последовательно зависит от предыдущего?В SQL нет аналога, а пользовательский агрегат, опять же, должен быть ассоциативным для параллелизации.
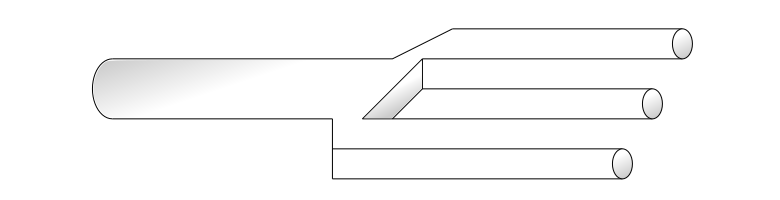
"Невозможная" параллельная реализация неотрицательной суммы всё же существует. Весь немногословный код поместим в
public class Example {
…
}Для тестирования создадим длинную историю псевдослучайных изменений, пусть распределённых на отрезке [-99, 99]
static LongStream changes() {
return LongStream
.range(1, 1000_000_000)
.map(i -> (i * 137) % 199 - 99);
}Чтобы на коленке оценить корректность и эффект от параллелизации, печатаем время вычисления и результат.
static void bench(ToLongFunction<LongStream> function, LongStream changes) {
long start = System.currentTimeMillis();
long result = function.applyAsLong(changes);
long end = System.currentTimeMillis();
System.out.printf("%4sms: %s\n", end - start, result);
}Проверим обычную сумму: вычисления параллелятся идеально и результат совпадает с последовательным. Догадайтесь, сколько ядер в процессоре?
bench(Example::usualSum, changes());
bench(Example::usualSum, changes().parallel());
> 1585ms: 147
> 390ms: 147Наивная реализация считается быстро, но неправильно при параллельном вычислении.
bench(Example::nonNegativeSum, changes());
bench(Example::nonNegativeSum, changes().parallel());
> 1274ms: 300
> 390ms: 13309Для верного параллельного решения познакомимся с группой Гротендика, которая позволяет представить целое, в том числе отрицательное, парой натуральных чисел
-2 ~ (5, 3) ~ (15, 13) ~ (105, 103) ~ …
где первый элемент пары трактуется как вычитаемое, а второй элемент — как уменьшаемое. Класс с двумя полями в представлении Гротендика будет хранить промежуточное состояние агрегата неотрицательной суммы.
static final class Gro {
private long fall;
private long grow;
}
Место для удара головой ????
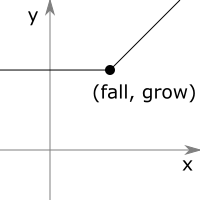
Семейство функций смещённых ReLU с двумя параметрами fall и grow, задающих точку излома, замкнуто относительно композиции. То есть y₂(y₁(x)) имеет такой же вид смещённого ReLU, ибо
max(0, a + max(0, b)) = max(0, a) + max(0, b + min(0, a))
Композиция функций ассоциативна, значит, композиция смещённых ReLU тоже ассоциативна.
Неотрицательную сумму реализуем через мутабельную свёртку Stream.collect():
Параллельным вычислителям раздаём по пустому агрегату
Gro::new;Агрегируем
accumulatorнезависимые куски данных;В конце попарно, сохраняя порядок кусков, объединяем через
combinerагрегаты всех вычислителей в один.-
Результатом из объединённого агрегата достаём только уменьшаемое, а про вычитаемое забываем.
static long grosum(LongStream changes) { return changes.collect(Gro::new, Example::accumulator, Example::combiner) .grow; } static void accumulator(Gro a, long value) { a.grow += value; if (a.grow < 0) { a.fall -= a.grow; a.grow = 0; } } static void combiner(Gro a, Gro b) { if (a.grow < b.fall) { a.fall += b.fall - a.grow; a.grow = b.grow; } else { a.grow += b.grow - b.fall; } }
Проверяем параллельную реализацию неотрицательной суммы: вычисления параллелятся отлично и результат совпадает с последовательным.
bench(Example::grosum, changes());
bench(Example::grosum, changes().parallel());
> 1277ms: 300
> 402ms: 300Исходники на разных языках: Java, SQL, Haskell, русский
Кроме кода на Java, можно глянуть SQL, реализованный пользовательским агрегатом на Oracle. В отличие от обычной ассоциативной и коммутативной sum, grosum ассоциативна, но некоммутативна. Поэтому требуется всегда указывать порядок.
select grosum(change) over (order by time) as balance
from changesЕсть реализация моноида на Haskell, которых хорош тем, что тесты в 2 строки.
prop_eq xs = grosum xs == foldl' (⊞) 0 xs
prop_monoid = monoid (mempty :: Gro Int)На русском языке можно посмотреть доклад, слайды и транскрипт.
Какая-то абстрактная магия в реальности работает на благо человека.
Комментарии (33)

middle
02.01.2022 14:28Можно посчитать сумму параллельно, а потом, получив её на финальном узле, за O(1) -- max.

gchebanov
02.01.2022 15:09+2Пример последовательности: 1 -2 3. Если считать правильно то получится: relu(1-2)+3=3; а если наивно: 2.
Легко понять что порядок важен: если переставить 3 в начало то переносов при сложении не возникнет, и результат совпадет, в то время как подход "сложить все" - теряет информацию о порядке.

unsignedchar
02.01.2022 16:37+2Забавно :) Но не понятна область применения.
Пример последовательности: 1 -2 3
Если это как-то относится к остаткам на складе или состоянию счета, то на этапе -2 нужно генерировать exception. Банкомат, например, либо выдает заказанную сумму, либо не выдает ничего.
deb Автор
02.01.2022 17:13Очень правильный вопрос. Подобрать подходящий инструмент под задачу и наоборот — полдела к успеху в любом начинании. Могу предложить варианты для
grosum:Кладовщик ограничен максимальной пропускной способностью — на входе потенциальный расход, а не фактический, который меньше.
Банкомат выдаёт максимум, сколько может.
Глязные данные, которые нужно почистить online или offline.
Запоздалые транзакции оформлены задним числом. Нужно быстро инкрементально за O(ln n) пересчитать хвост журнала.

unsignedchar
02.01.2022 17:44Запоздалые транзакции оформлены задним числом.
Это воще всё ломает. Если такое допустимо (транзакция уже оформлена) — её нельзя не проводить. Без овердрафта никак.
Сложно прогнуть реальный мир под стройные математические абстракции.
mayorovp
02.01.2022 17:48+1Но можно использовать конструкцию из статьи для валидации журнала, чтобы определить всё ли в порядке, или явно забыта ещё какая-нибудь транзакция.

mayorovp
02.01.2022 17:29О, кстати про исключения. Я только что понял, что случай "суммы с исключениями", во-первых, точно так же не является ассоциативным, а во-вторых вычисляется тем же самым алгоритмом, только с проверкой fall на последнем шаге:
static long grosumEx(LongStream changes) { Gro x = changes.collect(Gro::new, Example::accumulator, Example::combiner); if (x.fall > 0) throw …; return x.grow; }Но это только для случая, когда любое исключение ломает процесс. Если рассматривать модель банкомата, который при исключении продолжает работу с неизменным остатком (a+b<0? a: a+b) — то пара ⊕a ⊖b из моего комментария ниже перестанет редуцироваться до ⊖(b — a) и вся конструкция рассыпается.

mayorovp
02.01.2022 15:27+23В статье показана магия, но явно не хватает объяснений. И группа Гротендика тут ничего не объясняет, а лишь усложняет, потому что, к примеру, сложение в группе Гротендика отличается от операции combine.
Поэтому попробую раскрыть магию подробнее. Вот у нас есть операция ⊕, которая "неудобна" из-за отсутствия ассоциативности. Сопоставим теперь каждому числу a функцию fa(x) = x ⊕ a, эта функция выражает наше "намерение" прибавить a. Обозначим такую функцию (⊕a).
Теперь рассмотрим пару чисел a и b, и функцию-"намерение" для этой пары: ga, b(x) = (x ⊕ a) ⊕ b. Эта функция является композицией функций ⊕a и ⊕b: ga, b = (⊕b) ∘ (⊕a). Кстати, обозначим для простоты в дальнейшем такую функцию как ⊕a ⊕b. Теперь вспомним что композиция функций всегда ассоциативна, и мы получаем, что любую операцию можно "сделать" ассоциативной если перейти от исходного множества и операции к множеству функций-"намерений" над первым и композиции функций.
Кстати, по-научному "намерения" называются эндоморфизмами, а построенный нами моноид так и называется — моноид эндоморфизмов.
К сожалению, операция композиции функций ничего не вычисляет, а лишь откладывает вычисление, поэтому "в лоб" всё перечисленное выше не применить. Нужно найти какой-то способ упрощения сложных композиций, чтобы закодировать эндоморфизмы пригодным для вычислений способом.
Теперь переходим к самой "магии". Для начала, разделим все эндоморфизмы по знаку: здесь и далее,
⊕a означает функцию fa(x) = x ⊕ a, где a ≥ 0
⊖a означает функцию fa(x) = x ⊕ -a, где a ≥ 0Заметим, что намерения одного знака друг с другом складываются:
⊕a ⊕b = ⊕(a+b)
⊖a ⊖b = ⊖(a+b)Также заметим, что операции ⊕ и ⊖ могут компенсировать друг друга, но только если идут именно в этом порядке:
⊕a ⊖b = ⊕(a — b), если a ≥ b
⊕a ⊖b = ⊖(b — a), если a ≤ b(случай a=b тут разобран два раза, но это не ошибка, потому что ⊕0 и ⊖0 — одна и та же операция, и нет разницы как считать)
А вот последовательность операций ⊖a ⊕b никак не упрощается, поэтому в общем случае любая последовательность операций упростится до этой формы. Ну так давайте именно такую форму и выберем в качестве конструктивного представления "намерения"!
И так, любой интересующий нас эндоморфизм мы будем представлять в виде пары чисел (a, b): f(x) = (x ⊕ -a) ⊕ b, где a и b ≥ 0.
Теперь можно наконец-то выразить операцию композиции намерений:
(a, b) ⊕ (c, d) = ⊖a ⊕b ⊖c ⊕d = ⊖a ⊕(b-c) ⊕d = ⊖a ⊕(b-c+d) = (a, b-c+d), если b ≥ c
(a, b) ⊕ (c, d) = ⊖a ⊕b ⊖c ⊕d = ⊖a ⊖(c-b) ⊕d = ⊖(a-b+c) ⊕d = (a-b+c, d), если b ≤ cПроверяйте, эта формула соответствует функции combiner из поста. Функцию accumulator можно получить, если подставить в эту формулу формулу перехода от числе к намерениям. Ну а финальное получение поля grow в функции grosum — это ни что иное как подстановка x=0 в формулу эндоморфизма:
(a, b)(0) = (0 ⊕ -a) ⊕ b = 0 ⊕ b = b.

mayorovp
02.01.2022 15:33+6А вот применять неотрицательную сумму к складу я бы поостерёгся: отрицательный остаток на складе — явно исключительная ситуация, и молча исправлять такие ситуации в ноль — не совсем то, что ожидается от надёжной системы.
Опять-таки, если из пустого склада увезли 16 единиц продукта, а потом эту операцию сторнировали (что было отражено в журнале как +16 единиц продукта) — в итоге остаток должен быть 0, а не 16.
deb Автор
02.01.2022 16:49Зависит от целей, а не от того, что это склад. У нас, например, оптимизационная NP задача составления расписаний сотрудников, в том числе на складе. А быстрый инкрементальный пересчёт позволил считать на ноутбуке, а не на кластере.
Абстракция отличается от реальности и выбирать нужно подходящую под действия.
grosumничем не лучше и не хужеsum— ещё один кирпичик конструктора приложений.Кстати, в поле
fallнакопится сумма, которую нужно сторнировать, чтобы баланс сошёлся. Тоже может быть кому-нибудь полезно.
mayorovp
02.01.2022 17:08+1Э-э-э, ну уж нет. Коли история содержит недостоверные данные — сумма, которую нужно сторнировать, может быть найдена только по результатам инвентаризации.

dmanikhine
02.01.2022 15:40Большое спасибо за статью. Порекомендуйте пожалуйста литературу по функциональному программированию. У меня каша в голове от всех возможностей которые даёт фп. Хотелось бы привести это всё в порядок, но достойной книги где бы это всё хорошо разжёвывалось я пока не нашел. Заранее большое спасибо за любые ссылки или любую информацию.

csl
02.01.2022 17:42+1https://en.m.wikibooks.org/wiki/Haskell
Привожу в порядок этим, там и примеры (с ответами)
deb Автор
02.01.2022 17:52ФП не так далеко от ООП, как принято считать. Хотя одни и те же вещи называют разными именами.

dmanikhine
02.01.2022 20:25К сожалению "имена" не добавляют ясности и понятности.
Я раз пять прочитал Ваше "определение" Вариантности......ни чего не понял. Думаю что и после 50 прочтения тоже ничего не пойму..... Мне кажется дело не во мне, а в "определении" ))))) Возможно я ошибаюсь. (
Хотя Вариантность достаточно простая и понятная штука. Если конечно её просто и понятно объяснять.
Может есть смысл улучшить Ваше "определение" Вариантности?
Возможно пример того, как Вариантность можно использовать в реальном проекте, сделает Ваше "определение" Вариантности более понятным.
deb Автор
02.01.2022 21:27К сожалению, только читать бесполезно, хоть 5, хоть 1000 раз. В том посте ошибка — "определение" надо переназывать "понятиями" — сам только недавно научился различать. Прочитав множество имён снега, вы не научитесь ими пользоваться. Попробуйте написать для детей простой туториал езды на велосипеде. Мы можем понять друг друга только в деятельности.
Человеку вот понравилось описание функторов и монад, но думаю только потому, что он уже достаточно попрактиковался, наработал понятие и прочувствовал несколько примеров монад, чтобы их сравнить и найти между ними что-то общее.

dmanikhine
02.01.2022 21:50+1Напишу понятнее. Я знаю что такое Covariance and Сontravariance. Ваше "определение" "Вариантности" сложное и запутывает читателя. Когда читаешь Ваше "определение" возникает впечатление, что автор сам плохо понимает то о чем пишет.
IMHO Ваше определение "Вариантности" можно значительно улучшить.
Возможно есть смысл не использовать слово "Вариантность". А использовать Covariance and Сontravariance.
deb Автор
02.01.2022 22:15автор сам плохо понимает то о чем пишет.
IMHO Ваше определение "Вариантности" можно значительно улучшить.
А вот я в вас верю. Не держите в себе, пишите, улучшайте!

Stiver
02.01.2022 17:27А если считать действительно сумму, без инициализации аккумулятора нулем? Если правильно понимаю, вот эта строчка
return changes.reduce(0, (a, b) -> Math.max(0, a + b));
приводит к тому, что для списка (a,b,c,d...) мы считаем на самом деле 0 ⊕ a ⊕ b ⊕ c ⊕ d +… (вместо a ⊕ b ⊕ c ⊕ d + ...). Благодаря этому функция ⊕ у нас применяется всегда для неотрицательного первого числа, отсюда например и⊕a ⊕b = ⊕(a+b)
хотя в общем случае x ⊕ 1 ⊕ 2 != x ⊕ 3
mayorovp
02.01.2022 17:34Да, если разрешить начальному значению быть отрицательным — то ⊕a ⊕b перестаёт редуцироваться до ⊕(a+b) и всё рассыпается.
Но решение тут простое — надо разделить исходный список на "голову" и "хвост":
S ⊕ a ⊕ b ⊕ c ⊕ d +… = (S ⊕ a) ⊕ b ⊕ c ⊕ d +…
Здесь S ⊕ a всегда неотрицательное, а значит для хвоста можно использовать обсуждаемый алгоритм.
Точно так же решается задача и для случая, когда у нас вообще нет никакого аккумулятора, только теперь придётся выделить уже два элемента из головы списка:
a ⊕ b ⊕ c ⊕ d +… = (a ⊕ b) ⊕ c ⊕ d +…
deb Автор
02.01.2022 19:00Возможно, @mayorovp меня поправит, что он имел в виду. Я за круглым плюсом ⊕ вижу 2 смысла. Чтобы их не путать, введём квадратный плюс ⊞.
⊖fall отрицательный морфизм;
⊕grow положительный морфизм;
a ⊞ b = max(0, a + b) = relu(a + b), неудобная неассоциативная бинарная операция;кусок истории ((((x ⊞ a) ⊞ b) ⊞ c) ⊞ …) представим смесью морфизмов, парой
(⊖fall, ⊕grow).
Да, считаем (((0 ⊞ a) ⊞ b) ⊞ c) ⊞ …, как будто начинаем с пустого склада. Не забываем про неявные скобочки левой свёртки.
В общем случае верны оба:
(x ⊞ 1) ⊞ 2 = x ⊞ 3. Но неассоциативно.(⊕1)∘(⊕2) = (⊕3). Ассоциативно и в длинных скобки можно выражениях скобки можно опускать⊕a∘⊕b∘⊕c = ⊕(a+b+c). Но представление не полно, нужны ещё отрицательные морфизмы⊖, для записи произвольной истории нужна пара(⊖fall, ⊕grow).
Фух! Сложно объяснить простой код :(

mayorovp
02.01.2022 19:18+2Вам говорят, что (x ⊞ 1) ⊞ 2 не всегда равно x ⊞ 3. К примеру, (-2 ⊞ 1) ⊞ 2 = 2, в то время как -2 ⊞ 3 = 1.
Если начинать с пустого или хотя бы валидного склада — это не играет роли, но если начать со склада в невалидном состоянии — алгоритм отработает некорректно. Является ли это ошибкой — другой вопрос. Для случая со складом — наверное, нет. В общем случае — наверное, да.
deb Автор
02.01.2022 20:09Пример с
x=-2понятен, действительно, в этом случае будут проблемы, но не уgrosum. Дальше зависит от договорённостей, что такое общий случай :) Я предполагаюfallиgrowнеотрицательными, как у Гротендика, соответственно,xне может быть-2. В посте я ухожу даже от плавающей точки, чтобы не касаться неассоциативности при округлении. Опущены даже вопросы переполненияlong. Множество других вопросов остаются на совести разработчика приложения.Но алгоритм из поста,
grosum [-2, 1, 2] = 3 = grosum [1, 2] = grosum [3]. Алгоритм, который вернёт2или1— это некий другой, модифицированный алгоритм. Прежде чем рассуждать о нём, сначала необходимо зафиксировать его код.
mayorovp
02.01.2022 20:21Вам же с самого начала написали:
А если считать действительно сумму, без инициализации аккумулятора нулем?
Разумеется, grosum, считающая что в аккумуляторе настолько ноль, что его даже нет в алгоритме, для этого случая напрямую не подходит.
Вот вам обсуждаемая задача, если до сих пор не понятно:
changes.reduce((a, b) -> Math.max(0, a + b));
deb Автор
02.01.2022 20:53-1А если считать действительно сумму, без инициализации аккумулятора нулем?
Без примера кода точный смысл этого высказывания мне не ясен: инициализировать его чем-то другим, чтобы что сделать? Какой тезис обсуждаем?
Знаю только, что в неотрицательной сумме нет отрицательных чисел ни в начальном балансе
S, ни в промежуточном балансе (в том числе вS⊞a), ни даже в названии :) А из ложной посылки (Sотрицательно) можно вывести всё, что угодно, так что заранее согласен.
mayorovp
02.01.2022 20:56Вот вам пример:
changes.reduce((a, b) -> Math.max(0, a + b));Что тут непонятно-то? Как распаралелить этот код?
deb Автор
02.01.2022 21:51-1Этот код не полон. Перед тем, как параллелить, сначала типы поправьте: результат должен быть числом, что делать с
OptionalLong, почему и зачем?Был код, который решал задачу, вы его сломали и спрашиваете как починить? Не знаю, что может быть лучше, чем откатить коммит :) Вы хорошо разбираетесь в вопросе — ваш первый комментарий это показал. Уверен, вы правы, только я не понимаю постановку задачи, которую вы решаете — она у вас в голове. Ветка дискуссии разрослась, поэтому прошу в личку.

mayorovp
02.01.2022 21:54+1Чего именно тут не хватает?
что делать с OptionalLong
вернуть
почему и зачем
потому что задача такая

aamonster
03.01.2022 00:54+1Спасибо, было интересно, но почему работает – не понимал, пока не вывел алгоритм сам. Привычней всё-таки идти по старинке, не от монад, а от инвариантов цикла.


CrazyOpossum
Идея довольно простая, на самом деле. Но с моноидом внутри, действительно, получается красиво.
deb Автор
Tony Hoare