
Привет, Habr. В данный момент я разрабатываю игру про животных, где они должны беспорядочно бегать по карте. Идеей является то, что есть несколько видов животных, которые могут бегать только по своей территории, например:
Кошка, собака - по земле(Ground)
Рыбы и утки - по воде
и т.д.
В итоге я пришел к выводу, что зону проще всего разграничивать с помощью PolygoneCollider2D, как это реализовано в Cinemachine

Реализация №1(Медленный способ)
Я решил реализовать, что-то подобное, но только так, чтобы бралась на поверхности случайная точка и животное шло к ней. Поискав решение данной проблемы, я нашел лишь единственное решение:
public Vector3 PointInArea() {
var bounds = collider.bounds;
var center = bounds.center;
float x = 0;
float y = 0;
do {
x = UnityEngine.Random.Range(center.x - bounds.extents.x, center.x + bounds.extents.x);
y = UnityEngine.Random.Range(center.y - bounds.extents.y, center.y + bounds.extents.y);
} while (Physics2D.OverlapPoint(new Vector2(x, y), LayerMask.NameToLayer("Area")) == null);
return new Vector3(x, y, 0);
}
// https://forum.unity.com/threads/how-can-i-choose-random-points-inside-a-polygon-collider-2d.264985/Оно основано на взятии случайной точки по границам polygonCollider2D и проверка, что эта точка попадает на поверхность PolygonCollider2D.OverlapPoint();

Минус данного подхода, что он если polygonCollider2D сильно искажен, то while будет выполнятся долго. Но для моей игры нужны именно искаженная поверхность.
Я проверил, и даже вывел метод нахождения точки в отдельный поток, но все равно скорость поиска меня не устраивала, тем более имелись проблемы со синхронизацией List с параллельными потоками.
Вывод по методу:
Плюсы:
Быстрый в реализации
Минусы:
Медленный в бою
Нельзя использовать со сложными геометриями
Реализация №2
Далее я решил уже пораскинуть мозгами и попробовать решить задачу математическим путем:
если выбрать 2 соседние вершины у многоугольника
найти случайную точку между ними
найти центр многоугольника
polygonCollider2D.bounds.centerи выбрать случайную точку между координатами центра и случайной точки между вершинами.

Как можно увидеть на втором примере, отрезок, образованный случайной точкой между двумя соседними вершинами и центром может выходить за пределы площади, а это мне не нужно.
Я порыскал по просторам интернета и нашел интересную статью: Generating Random Points within a Polygon in Unity. В ней автор пишет свою реализацию поиска точки в многоугольнике, но решает это для трехмерного пространства, а меня интересует 2D, но из этой статьи я узнал о методе разбиения многоугольника на треугольники(Delaunay triangulation).
Pеализацию этого алгоритма я нашел на C# в GitHub у k-j0 (сам алгоритм ТЫК).
С этими знаниями я придумал новый алгоритм:
Разбиваем многоугольник на треугольники с помощью алгоритма k-j0
Выбираем случайный треугольник
Ищем точку между двумя случайными две случайные вершинами, выбранного треугольника
Ищем центр тяжести треугольника по формуле
-
Находим случайную точку на отрезке ((3 пункт) и (4 пункт))
Вуаля, теперь точка попадает со 100% шансом на площадь многоугольника.
Переносим в Unity
Разбиваем polygonCollider2D на треугольники методом Triangulator.Triangulate
List<Triangulator.Triangle> _triangles =
Triangulator.Triangulate(polygonCollider2D.points.ToList());
Triangulator.Triangle triangle = _triangles[Random.Range(0, _triangles.Count)];Ищем две случайные вершины треугольника
Vector2 onePoint = Vector2.zero;
Vector2 twoPoint = Vector2.zero;
switch (Random.Range(0, 3))
{
case 0:
onePoint = triangle.a;
twoPoint = triangle.b;
break;
case 1:
onePoint = triangle.b;
twoPoint = triangle.c;
break;
case 2:
onePoint = triangle.a;
twoPoint = triangle.c;
break;
}Находим центр тяжести треугольника
Vector2 center = triangle.centerOfMass();Далее нам нужно находить случайную точку между двумя точками. Для этого реализуем метод RandomPointBetween2Points, который возвращает Vector2
private static Vector3 RandomPointBetween2Points(Vector3 start, Vector3 end){
return (start + Random.Range(0f, 1f) * (end - start));
}Находим случайную точку между вершинами
Vector2 randomBetween2Vector = RandomPointBetween2Points(onePoint, twoPoint);И в итоге генерируем готовую точку
Vector2 randomPoint = RandomPointBetween2Points(center, randomBetween2Vector);Теперь метод можно вызывать легко и просто:
Vector2 point = RandomPoint.GetRandomPoint(polygonCollider2D);Протестируем функцию на poligonCollider2D и найдем 100 точек

А 10000?

ВАЖНО! Нужно учесть, что точки генерируются относительно PolygonCollider2D, поэтому их потом следует приводить к Мировым координатам
Все ссылки и источники:
Исходники: https://github.com/LivelyPuer/RandomPoint
Haze Triangulator: https://github.com/k-j0/haze-triangulator
Готовый проект можно скачать ТУТ!
Спасибо за внимание!
Комментарии (10)

SadOcean
08.02.2022 15:13Я решал похожую задачу для неровных поверхностей чуть по другому, с помощью ускоряющей структуры.
Задача легко разбивается на 2 - выбор случайного треугольника и выбор случайной точки на нем.
Первую задачу для некоторых случаев можно решать наивно - выбрать просто случайный треугольник. Это будет работать плохо, если в меше есть треугольники с очень разной площадью. Второй вариант - найти площади всех треугольников, просуммированный вариант сложить в сортированный массив и выбирать бинарным поиском.
Найти случайную точку на треугольнике достаточно легко - находим такую в квадрате с размером 1 (случайный X/Y), потом те точки, для которых x + y > 1 разворачиваем (умножаем на -1), а потом X умножаем на вектор AB целевого треугольника, а Y - на AC и складываем.

SadOcean
08.02.2022 15:17Да, естественно алгоритм исходил из того, что тесселяцию искать не нужно - у нас ведь есть данные меша, который отправляется в коллайдер.
Ускоряющая структура соответственно состояла из массива, который содержал суммы площадей треугольников для поиска взвешенного случайного и вектора AB/AC для поиска точки

iROOT
08.02.2022 15:30Про равномерное распеделение точек были статьи, например этот перевод https://habr.com/ru/post/440316/.
Я первое что подумал это поискать про вычисление площади треугольника (полигонов) методом Монте-Карло.

DimPal
08.02.2022 16:06Площадь треугольника вычисляется за пару сложений и умножений, зачем Монте-Карло? Если точек много, то целесообразно после триангулизации посчитать площади каждого треугольника, затем, зная нужное количество точек вычислить сколько точек для каждого треуголника (пропорционально площади), и наконец, сгенерировать в каждом треугольнике нужное количество случайных точек. Все. Задача для школьников.

Flux
08.02.2022 18:08Если уж вы всё равно делаете триангуляцию, легко допилить алгоритм чтобы он выдавал действительно равномерно распределенные точки.
Сначала выбираете треугольник в котором будет лежать конечная точка, вероятность выбора треугольника пропорциональна его площади. Можно использовать, например, reservoir sampling.
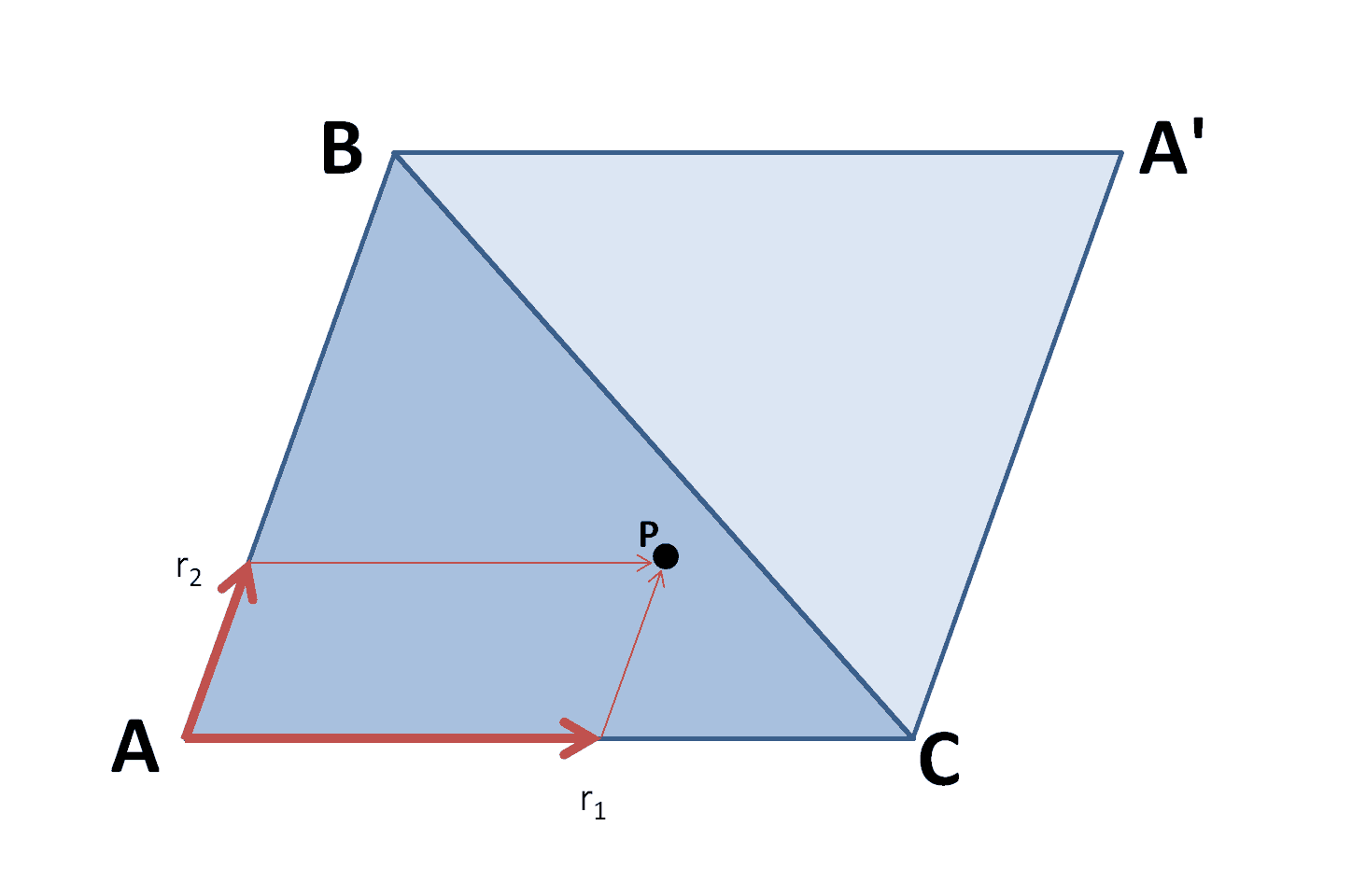
После этого выбираете случайную точку в треугольнике. Ваш метод, к сожалению, выдаёт неравномерное распределение что видно даже в вашем примере с 10к точек. Лёгкий способ — в уме дополнить треугольник до параллелограма как на картинке ниже. Становится очевидным что можно выбрать случайную точку в единичном квадрате, если она попала в верхний треугольник — отразить относительно центра, а потом перемапить базисные вектора с (0, 1), (1, 0) на AB, AC.



Ingvarior
Я бы немного усовершенстовал алгоритм. Если вы хотите добиться действительно случайного выбора точки и маскимально равномерного распределения.
Ибо сейчас выбор точки вовсе не случайный как минимум потому что площади треугольников разные. А вы выбираете их случайно с одинаковой вероятностью. На треуголниках более менее одинакового размера не очень заметно. Но даже на вашем скрине видно, что маленькие заполненны сильнее.
Нужно сделать, чтобы вероятность была взвешена относительно площади треугольника, то бишь равна площади треугольника деленной на площадь всей фигуры.
Ну и по поводу генерации случайной точки внутри самого треугольника, я бы тоже немного подумал. Для равносторонних треугольников ваш аглоритм возможно работает исправно. Но здесь вы опять же не учитываете разные длины сторон треугольника, при этом выбирая их с одинаковой вероятностью. На скрине это тоже заметно немного, что есть четкие зоны с большей и меньшей плотностью распределения
LivelyPuer Автор
Спасибо за комментарий, я учту ваши замечания для улучшения алгоритма поиска!
Если Вы хотите помочь в модернизации работы программы, то исходный код открыт на GitHub
Alexandroppolus
Даже для них - не совсем. Как я понимаю, выбор точки на стороне треугольника (п.3) и выбор точки на отрезке между п.3 и центром масс (точка О) делается с равномерной вероятностью по отрезку. Соответственно, приоритет будет у точек, которые лежат вблизи перпендикуляра от т.О до стороны (он самый короткий из отрезков), и разумеется у точек вблизи т.О.
На самом деле, не надо здесь точку О. Пусть у нас треугольник АВС, то просто берем случайную точку М на стороне ВС, потом случайную точку на отрезке АМ. И остается смекнуть такие функции распределения вероятностей на отрезках ВС и АМ, чтобы вышеописанных проблем не было.
Tiriet
если мы выбираем центр треугольника, из него пускаем случайный луч, и на этом луче случайно ставим точку- перпендикуляры к сторонам короткие, а лучи, идущие в углы- длинные, и на этих лучах плотность точек будет разная, вне зависимости от равносторонности или равнобедренности треугольников. Равномерное распределение точек по треугольнику можно получить примерно так: пусть треугольник задан точками А1, А2, А3.
возьмем два базисных вектора
b1=А2-А1 и b2=А3-А1.
возьмем два весовых коэффициента
k1=Rand(1.0) и k2=Rand(1.0);
Если k1+k2<1.0
построим точку Р= A1 + k1*b1+k2*b2,
иначе- построим точку P= A1+ (1-k1)*b1+(1-k2)*b2.
векторы b1 b2 задают параллелограмм A1,A2,A2+A3-A1,A3.
k1*b1+k2*b2- случайная точка в этом параллелограмме с равномерным распределением. k1+k2>1- условие того, что эта точка находится в этом параллелограмме за диагональю A2-A3. В этом случае мы отражаем эту точку относительно диагонали А2-А3, возвращая ее в требуемый нам треугольник и сохраняя равномерное распределение точек.. А если k1+k2<1- то точка сразу попала в исходный треугольник, и ничего делать не надо. И все это почти минимумом операций.
И обязательно надо выбирать вероятность попадания в треугольник не согласно его порядковому номеру, а по площади. То есть, каждому треугольнику присваиваем вес
S_summ = Summ(TriangleArea)
w[k]= Triangle[k].Area/S_summ;
а потом для поиска нового случайного треугольника делаем что-то типа такого:
r= Rand(1.0)
k=0
while (r>w[k]) {
r -= w[k]
k++
}
return k
Вам, судя по задаче, производительность расчетов не суть как важна, да и на равномерность распределения точек по полигону Вам тоже, видимо, можно закрыть глаза, если бы все треугольники были примерно близкой площади. Но лучше все-таки использовать аккуратные алгоритмы. А вот если в триангуляции вдруг вылезет область, где будет много мелких треугольников- то тогда Ваши коты будут тереться именно в ней, изредка выбегая в большие треугольники, и это будет заметно.
z0ic
Или как на сфере, чтобы точки не скапливались у полюса, применяют релаксацию.