В наше время информационные технологии развиваются с невероятной скоростью, и поэтому поддержание информационной безопасности является неотъемлемым атрибутом любой организации, а знаменитое высказывание братьев Ротшильдов «Кто владеет информацией, тот владеет миром» актуально как никогда. В сущности, информационные технологии являются одним из главных элементов предприятия, который поддерживает работоспособность бизнеса и повышает его эффективность и конкурентоспособность.

В условиях информатизации общества стоит уделять большое внимание таким информационным активам предприятия как конфиденциальные и персональные данные. Возможные последствия утечки этой информации всегда будут оказывать негативное влияние на эффективность деятельности организации.

Применение современных для настоящего времени средств безопасности, таких как антивирусное программное обеспечение и межсетевые экраны, позволяет выполнять функции защиты информационных активов лишь на высоком уровне, используя готовые криптографические примитивы, в то время как именно из них и слагается степень надёжности тех или иных элементов. Именно поэтому криптография является краеугольным камнем всех аспектов защиты информации.

На сегодняшний день максимальная разрядность ключа, который возможно подобрать прямым перебором, составляет порядка 74 бит, что означает допустимых значений. Но даже такой результат был достигнут за четыре с лишним года, и как следствие подобный метод в большинстве случаев гарантирует потерю информативности данных на момент их получения. Все разработанные методы поиска ключа в той или иной степени должны позволять находить его за время меньшее, чем потребовалось бы для полного перебора всех значений.

Подобные методы, два из которых линейный (ЛК) и дифференциальный криптоанализ (ДК), впервые были изложены в работах Ади Шамира в начале 90- годов. На тот момент стандартом де-факто являлся алгоритм DES (Data Encryption Standard), и публикации о методах его анализа носили скудный характер. В 2001 году был разработан алгоритм AES (Advanced Encryption Standard), который обладает большей стойкостью как минимум из-за большего размера ключа. Несмотря на это, DES до сих пор является основой многих защитных систем. Это связано в первую очередь с особенностями аппаратной реализации алгоритмов и размером вырабатываемых ключей. Более того, стандарт по-прежнему рекомендован для использования в коммерческих структурах.

Общий принцип обоих методов заключается в сравнении открытого и закрытого текстов, и выявлении закономерностей при наличии определенных криптографических примитивов, числа раундов и структуры самого алгоритма. Конечно, это требует наличия n-го числа пар открытого и закрытого текста, но число операций, необходимое для вскрытия ключа, существенно меньше, нежели в случае с полным перебором. Именно поэтому реализация оных методов носит актуальный характер.

Отметим еще раз, что ранее алгоритмы шифрования тестировались путём возможности использования метода полного перебора, и, несмотря на всю простоту данного метода, ложка дёгтя была в огромном количестве вариантов значений ключа, так как даже для самой относительной малой (для DES она составляет 56 бит) длины количество вариантов составляло . И даже несмотря на то, что современные компьютеры позволяют перебрать столь большое число вариантов за приемлемое время, для алгоритма AES, где 128 битный ключ, такая возможность отсутствует.

Именно этот факт поспособствовал появлению новых методов получения секретного ключа, в частности ЛК и ДК, а также пересмотру взглядов на криптографию в целом, так как подобные новшества породили более высокие требования к алгоритмам шифрования. Использование подобных методов позволяет сократить время поиска ключа, то есть уменьшить сократить количество операций (в случае с DES) в среднем до , причем число исследуемых пар текстов должно составлять около , что всё равно меньше .

Итак, для начала рассмотрим работу алгоритма DES. В основе его работы лежит однородная, сбалансированная сеть Фейстеля (т.к. сообщение разбивается на равное количество битов, а функция F одинакова каждый раунд). На рисунке 1 изображена структура алгоритма. Его работа такова: на вход поступает последовательность из 64 бит, после чего каждых из них подвергается перестановке. Далее полученная последовательность проходит через сеть Фейстеля 16 раз, а затем снова подвергается обратной перестановке. Для DES-подобных алгоритмов уже после 8-го раунда наблюдается строгий лавинный эффект, так что 16-ти раундов вполне достаточно для надежного шифрования данных.

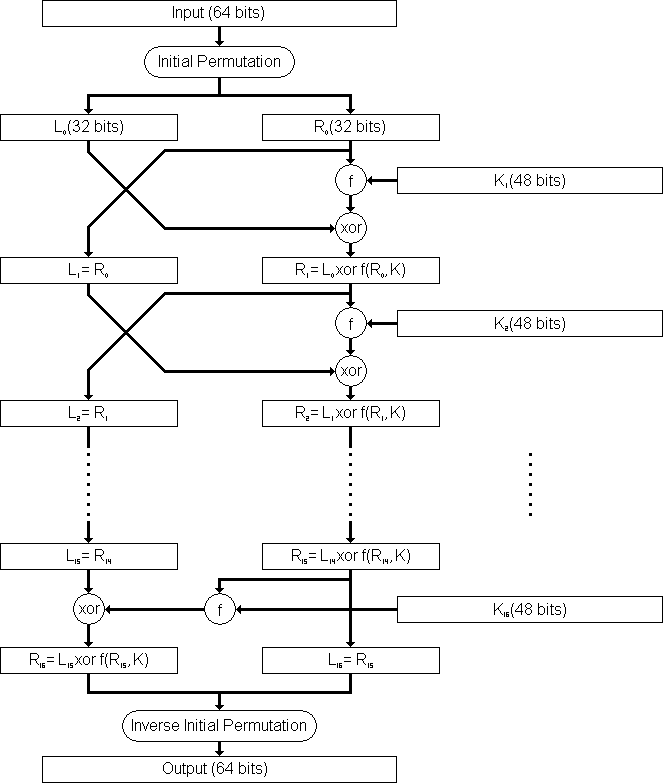
Основным ядром подобных алгоритмов является раундовая функция F, алгоритм работы которой представлен на рисунке 2. Правая часть текста подвергается расширению до 48 бит, после чего складывается с раундовым ключом по модулю 2. Такие операции как перестановка и расширение линейны по отношению к входным данным, то есть:

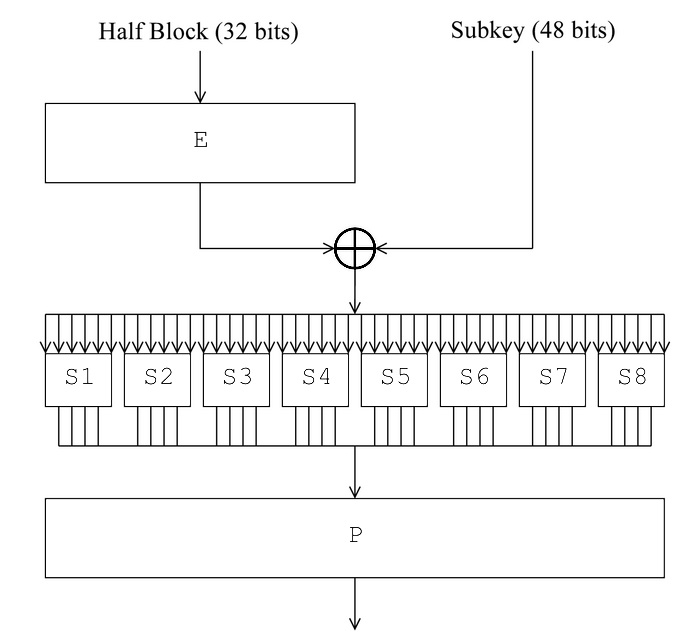
Однако, S–блоки подстановок не являются линейными, что положительно влияет на стойкость шифра, но вместе с тем затрудняет задачу криптоанализа. Идея метода ДК базируется на последовательном сравнении дифференциалов до и после выхода из S–блоков. Рассмотрим пример. Возьмем дифференциал . Подберем два таких открытых текста, для которых . Из равенства (2) мы можем получить последовательность , не вычисляя по отдельности расширения открытых текстов. Далее к ним добавляется раундовый подключ . Но, он добавляется как к первому тексту, так и ко второму, и поэтому не влияет на конечную разность. То есть:

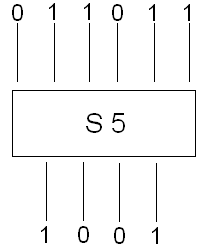
Рассмотрим детально работу S–блоков. На вход каждого из них поступает 6 битов, а на выходе 4. На рисунке 3 изображен пример работы пятого S–блока. Два крайних бита последовательности 0 и 1 обозначают первую строку таблицы подстановки, а 4 в середине,1101, 13 столбец. На их пересечении находится число 5, то есть, 1001 в двоичном виде. Очевидно, что всего может быть 64 входных дифференциала, а на выходе лишь 16.

Последовательно перебирая каждый дифференциал мы можем убедиться, что те или иные значения получаются с разной вероятностью. Сформулируем алгоритм  составления статистики для произвольного S–блока:

1. Возьмем дифференциал .  Подберем два таких открытых текста, для которых .

2. Каждое значение прогоняем через анализируемый S–блок.

3. Затем складываем между собой получившиеся значения.

4. Далее подбираем другое значение , которые так же в сумме дают исходный дифференциал и возвращаемся к пунктам 2 и 3.

5. Так продолжаем раз, где n – разрядность входа S–блока.

6. После подсчитываем число похожих выходных разностей.

7. Берём следующий дифференциал, и так раз.

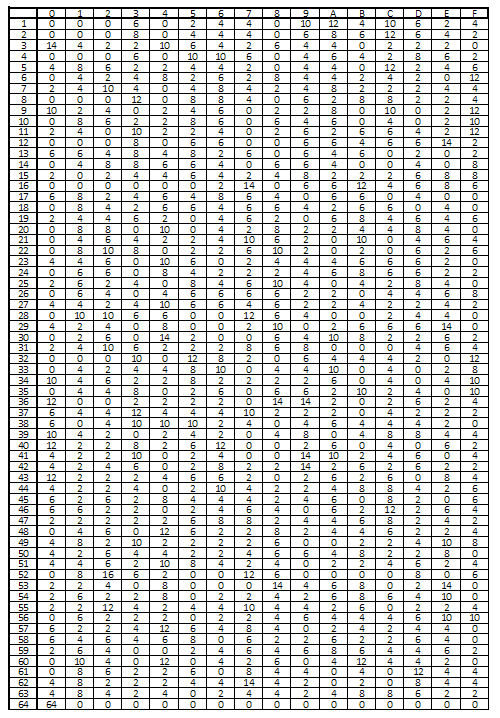
Данные,  полученные в результате анализа первого S–блока содержатся в таблице 1. Далее, по полученным характеристикам находят правильные пары текстов. Это те входные значения, которые соответствуют входным разностям из статистики каждого S–блока, то есть, соответствующая несходству чаще остальных. Именно эти найденные пары помогут вскрыть подключ последнего раунда.

Для поиска правильных пар лучше всего подавать на вход дифференциал такой, чтобы на выходе из F – функции первого раунда он давал левую часть исходного текста. Например, подобным дифференциалом может послужить . Правая часть пройдя через раундовую функцию F с большой вероятностью даст , что при сложении с левой похожей частью даст в свою очередь 0. В результате, на выходе мы с определенной вероятностью будем иметь ту же разность . Пара текстов, при которых подобное соответствие получилось,  будет правильной парой. Для успешной атаки на 16 раундовый DES необходимо рассмотреть пар.

Так же, стоит учесть, что в приведенной таблице 1 есть нулевые значения, то есть те, которые никогда не могут появиться. Например, при входной разности 7 значение никогда не сможет получиться. Таким образом, если из каждой таблицы исключить невозможные дифференциалы, количество операций на поиск правильных пар сократится на 25%. Для нахождения подключа последнего раунда на вход функции F подают найденную разность и анализируют выходные значения, перебирая разные значения подключей. Тот подключ, который будет появляться чаще остальных и будет искомым. Найденные 48 бит позволят без труда найти остальные 8 до полного восстановления ключа. Используя парадокс дней рождений можно посчитать, что для нахождения верного значения с вероятностью больше чем 0,5 необходимо перебрать пар.