В данной статье на конкретном примере рассматриваются особенности применения различных методов поворота 3D объекта в пространстве. В частности, сравнивается применение углов Эйлера и кватернионов.
Данная статья пригодится вам, если вы уже прочитали определение кватерниона и давно ищете наглядный материал для того, чтобы понять, зачем придумали кватернионы, и чем же они отличаются от углов Эйлера.
Наглядная демонстрация поворота по углам Эйлера уже была описана в статье на Хабре, особенно интересно поиграть с моделью самолётика (ссылки на программу в той же статье внизу).
Заручившись помощью чудесного сайта tinkercad.com представляю вам более наглядную демонстрацию поворотов предмета по углам Эйлера и сравнение с поворотом на основе кватерниона.
Демонстрация поворотов по углам Эйлера
Поворачивать будем избушку на курьих ножках. Вот ссылка на модель: Izba3D.
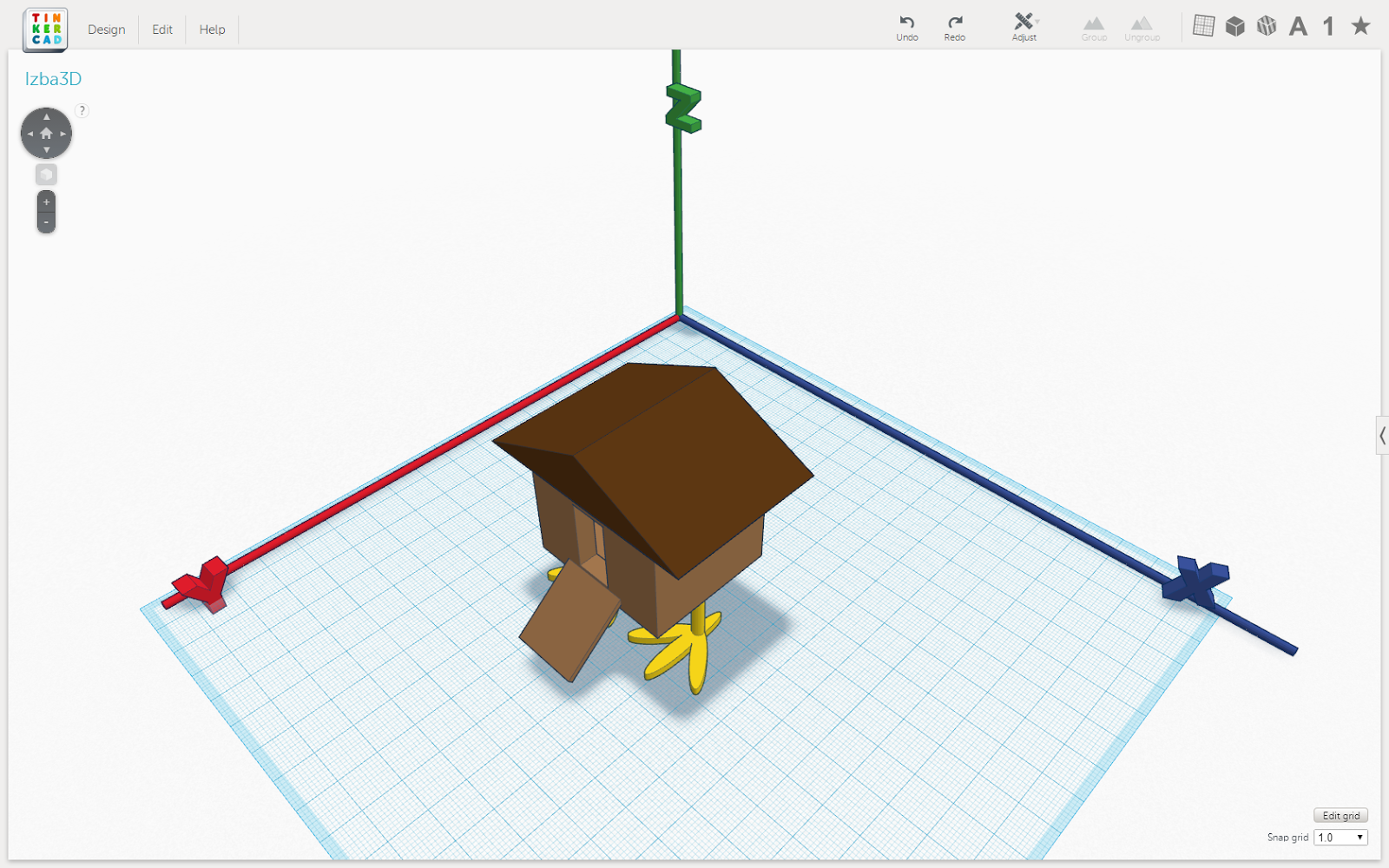
Рис. 1. Избушка в изометрии
Поворот вокруг оси Z, а потом оси Y
- Повернуть на 90 градусов вокруг оси Z
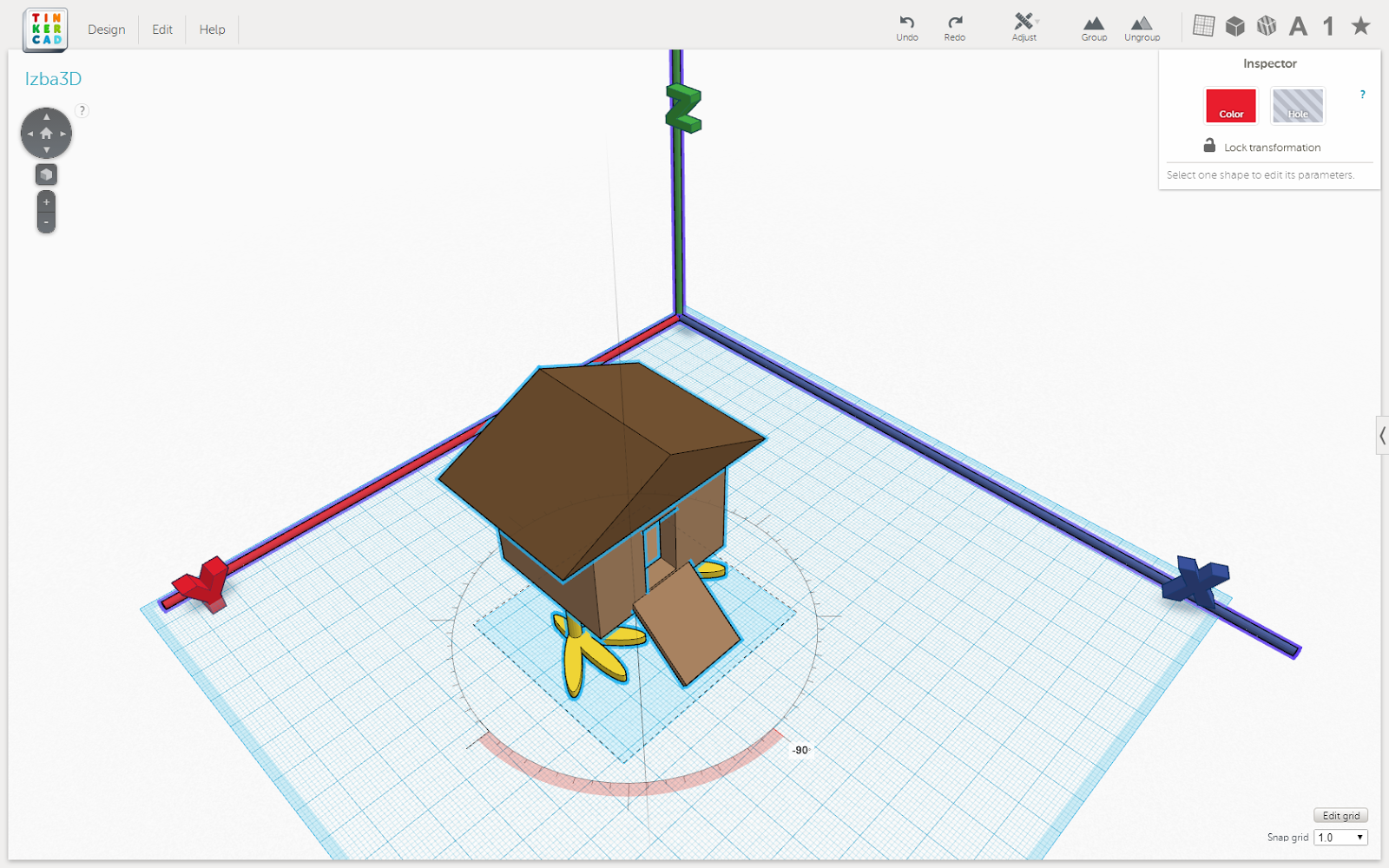
Рис. 2. Результат поворота рисунка 1 на 90 градусов вокруг оси Z
- Повернуть на 90 градусов вокруг оси Y
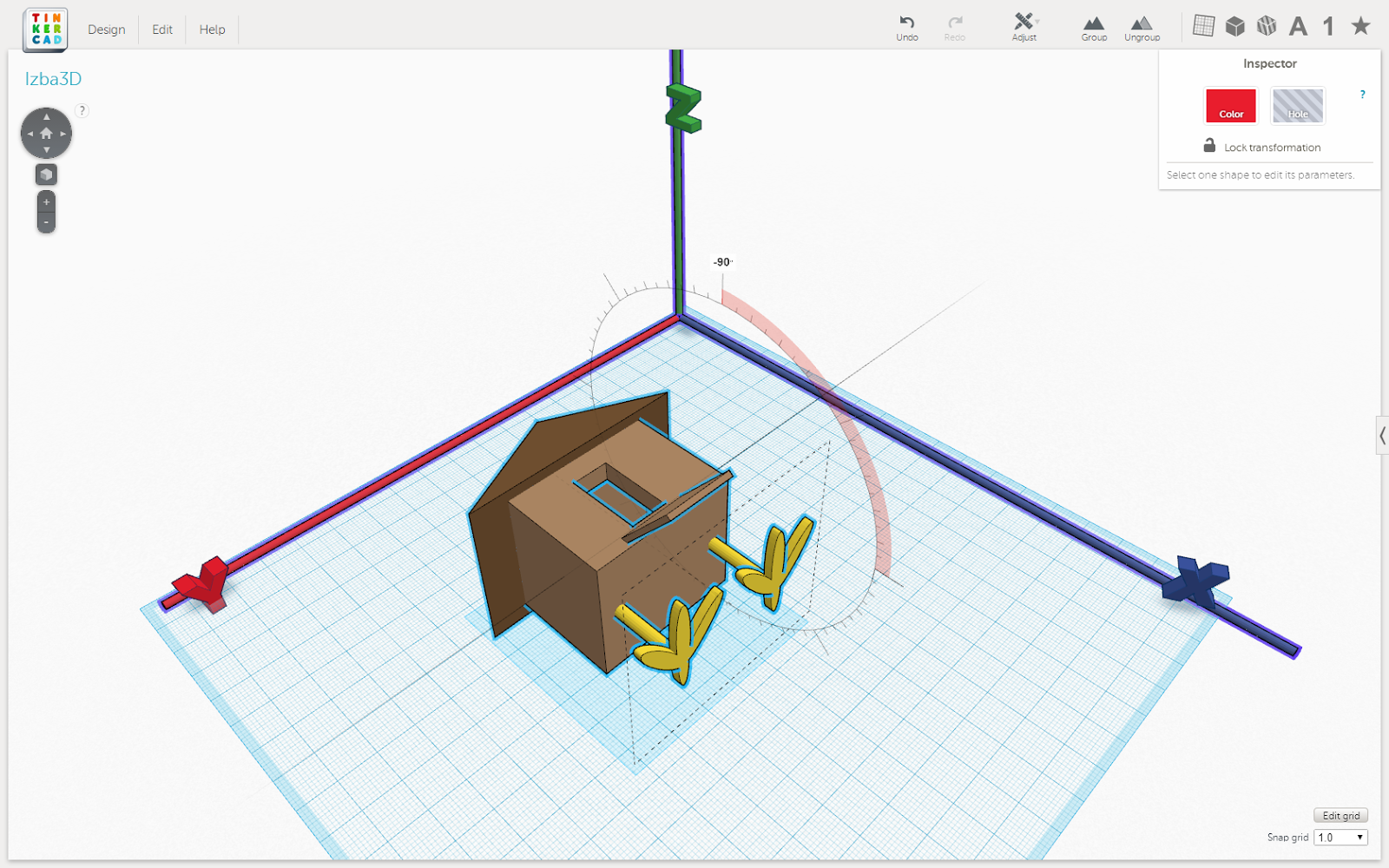
Рис. 3. Результат поворота рисунка 2 на 90 градусов вокруг оси Y
Поворот вокруг оси Y, а потом оси Z
- Повернуть на 90 градусов вокруг оси Y
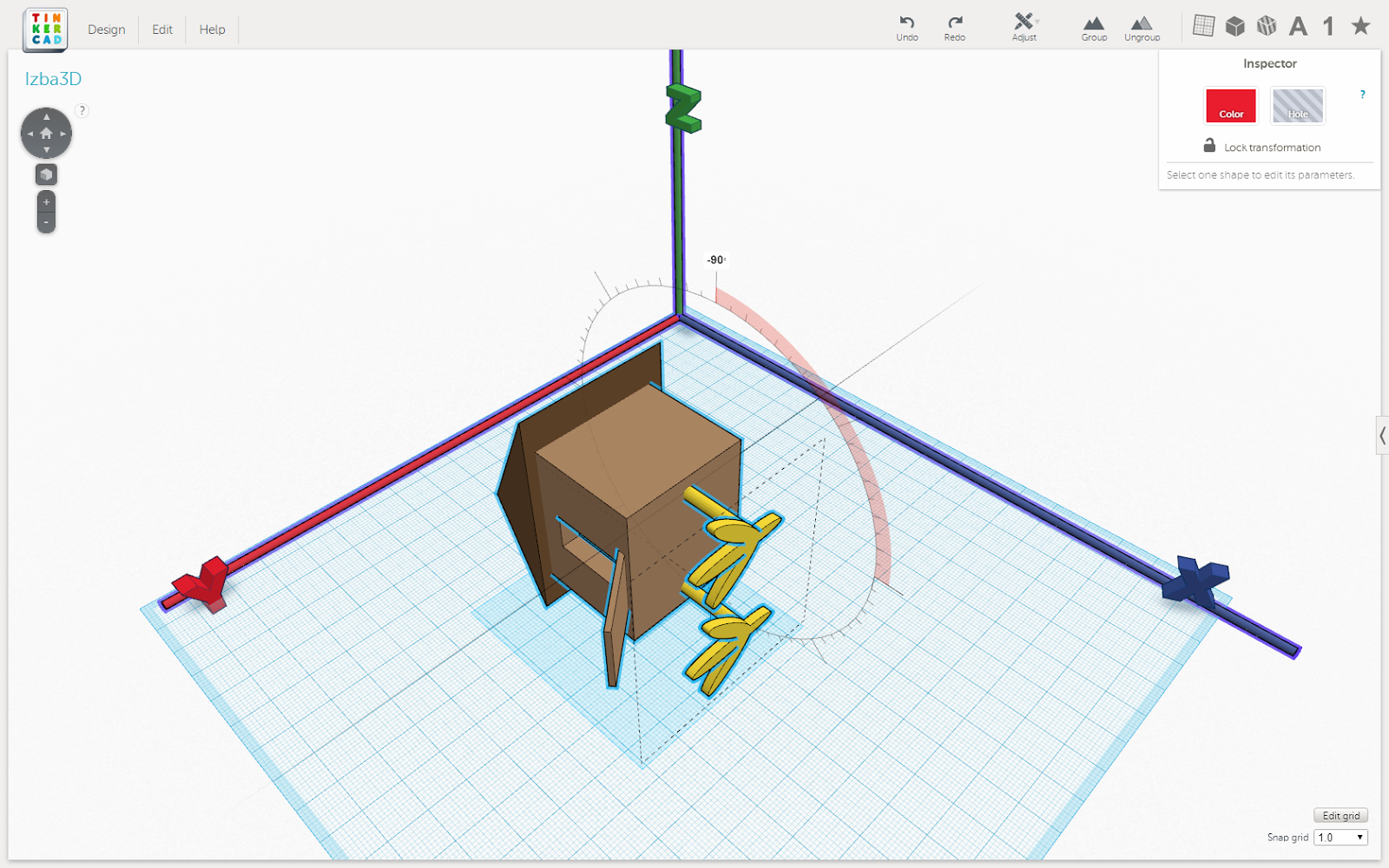
Рис. 4. Результат поворота рисунка 1 на 90 градусов вокруг оси Y
- Повернуть на 90 градусов вокруг оси Z
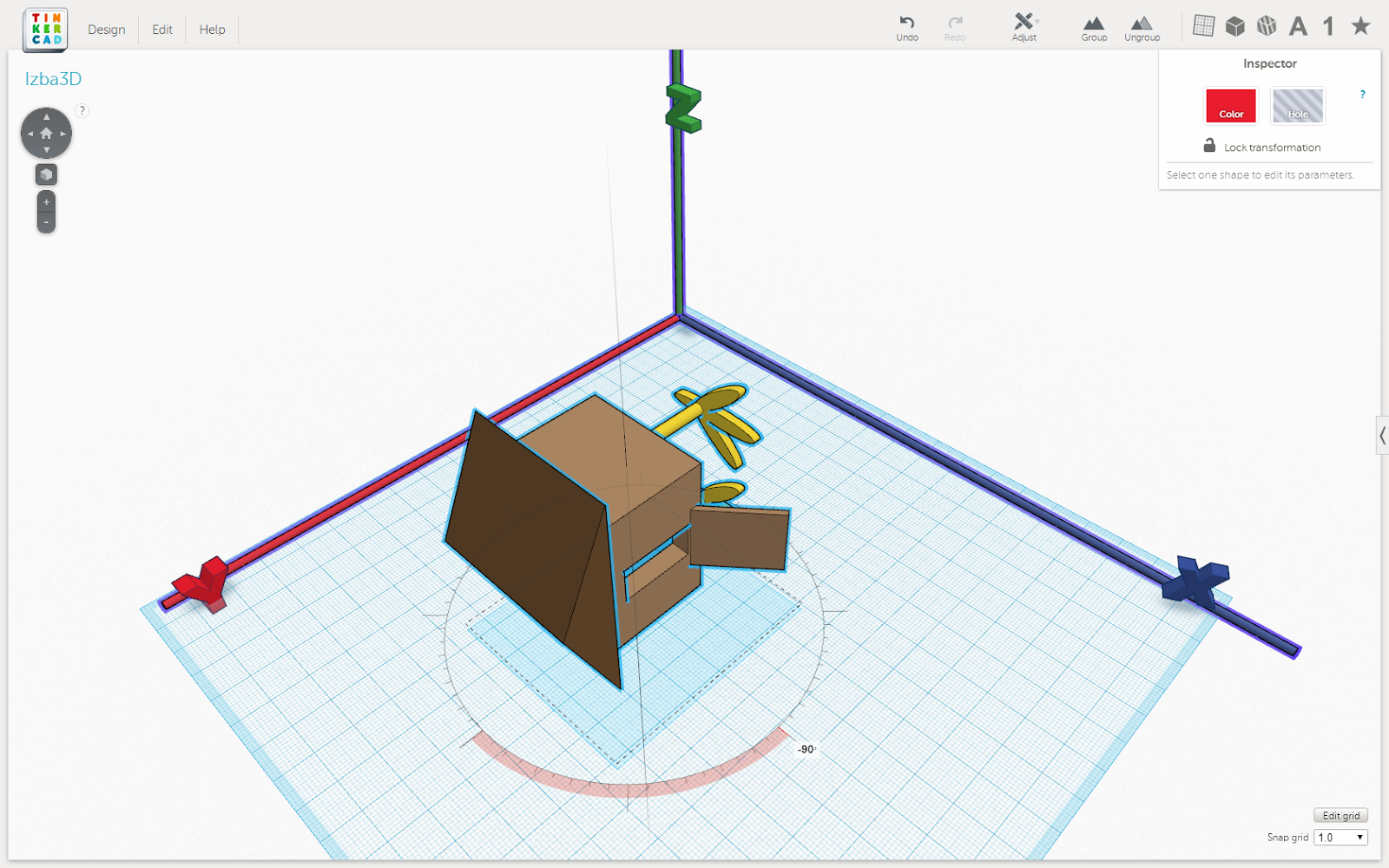
Рис. 5. Результат поворота рисунка 4 на 90 градусов вокруг оси Z
Сравнение и выводы
Сравним получившиеся картинки:

Рис. 6. Сравнение результатов поворота
Вывод: Порядок применения поворотов влияет на результат.
Кватернион
Гораздо удобнее пользоваться кватернионом, а именно, вектором и величиной поворота вокруг этого вектора.
Допустим, мы хотим повернуть избушку вокруг зелёного крылечка на 90, а потом снова на 90 градусов. Тогда пусть направление вектора совпадает с направлением зелёного крылечка.
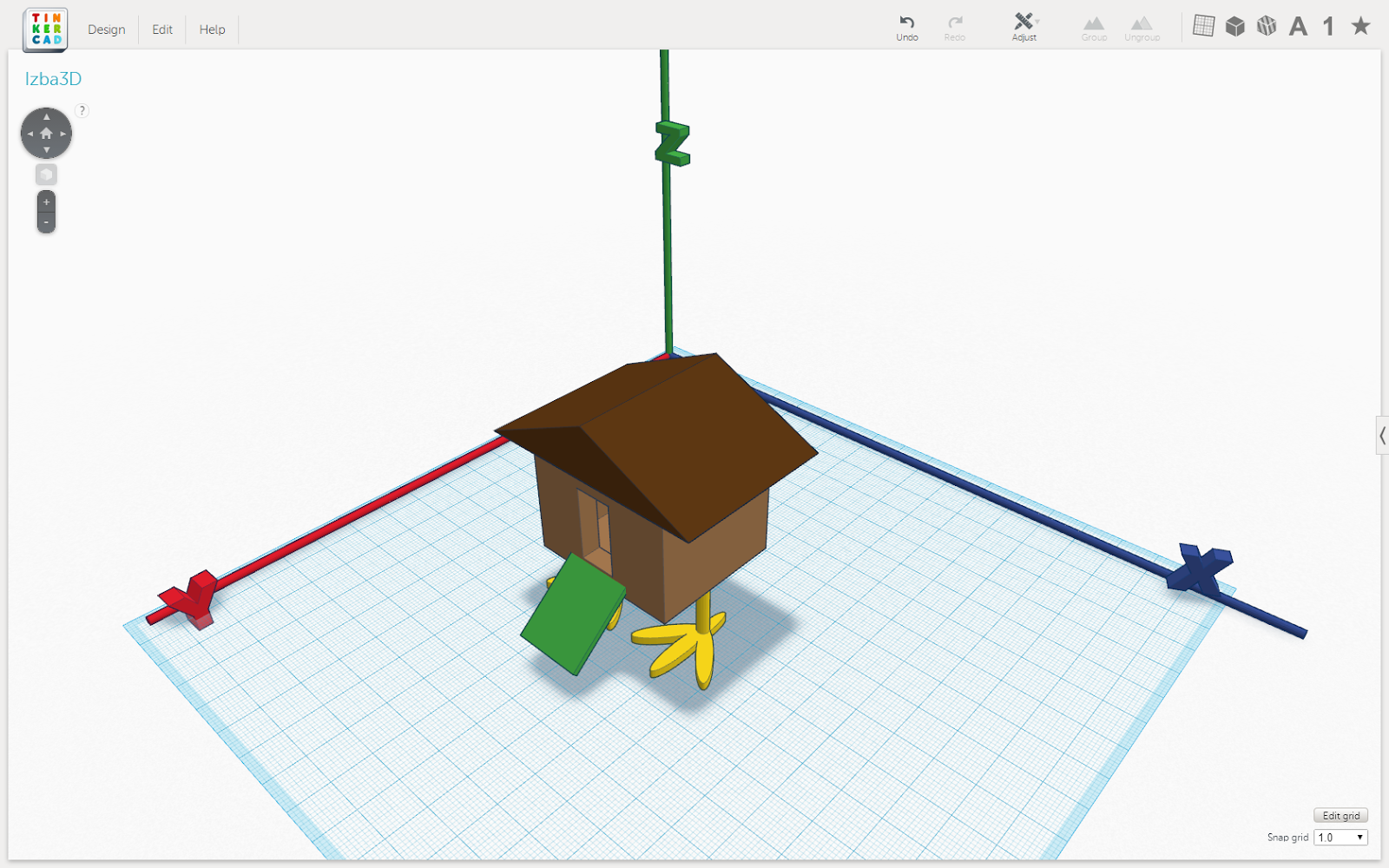
Рис. 7. Избушка на курьих ножках с зелёным крылечком
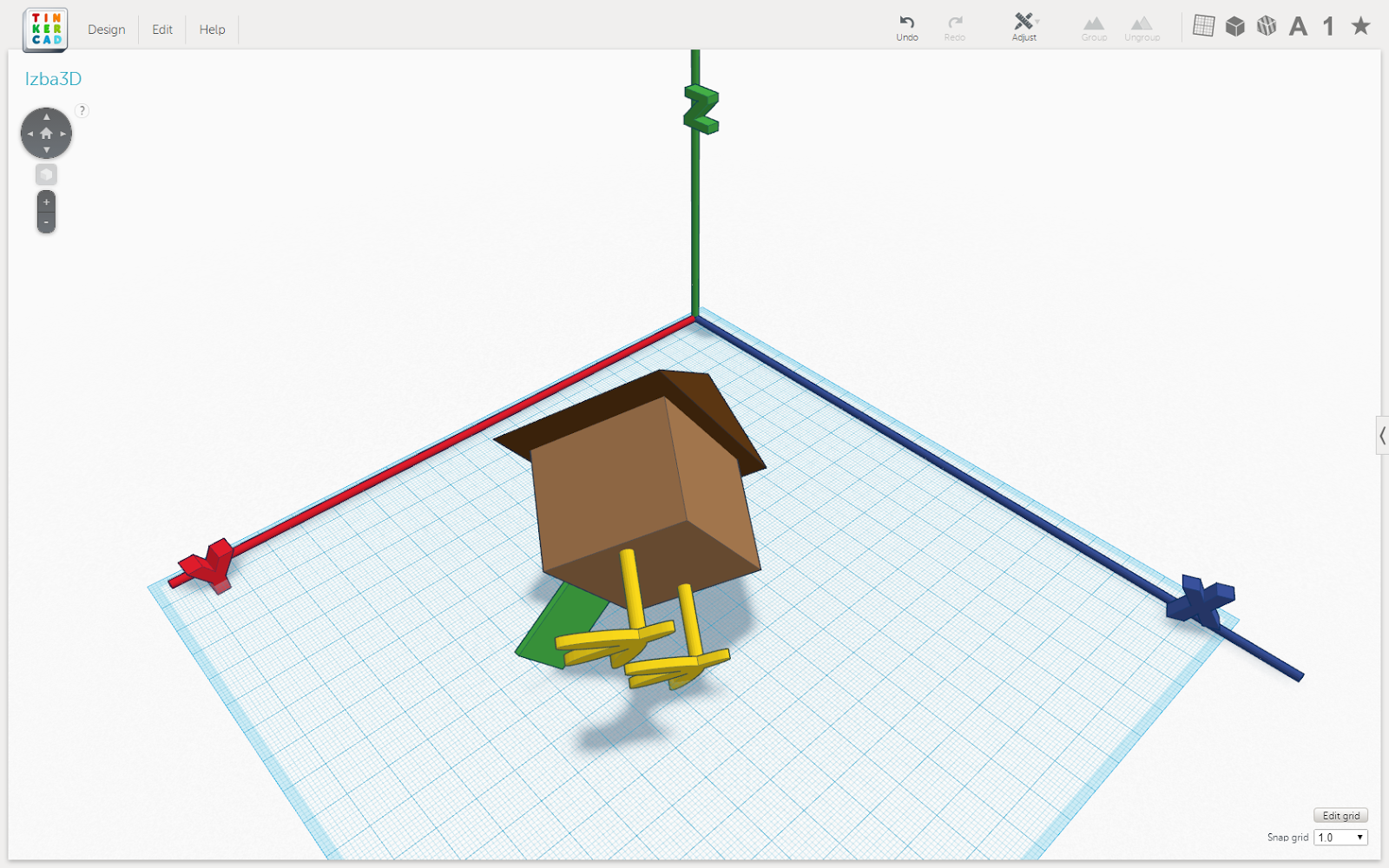
Рис. 8. Поворот на 90 градусов вокруг вектора, совпадающего с крылечком
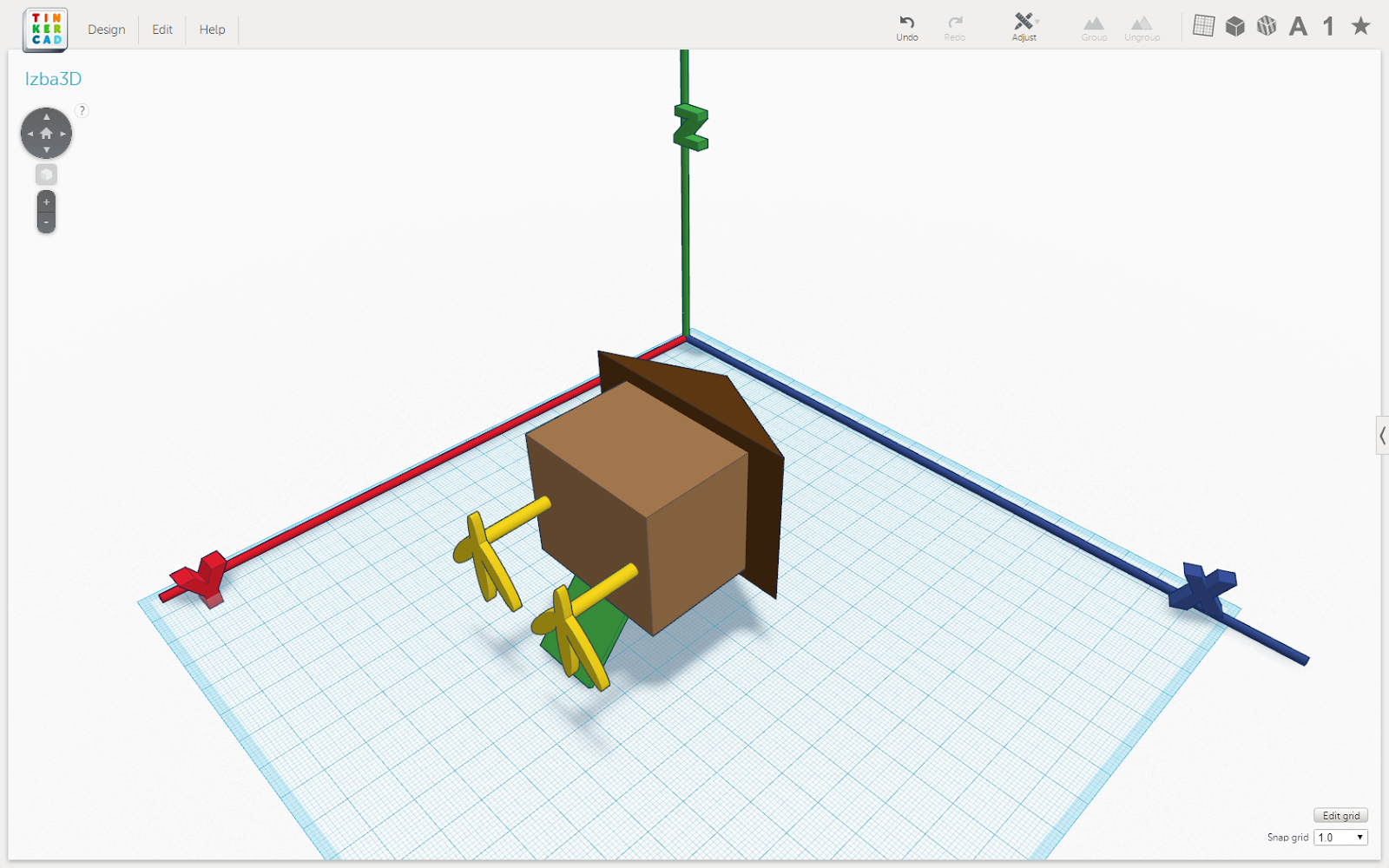
Рис. 9. Второй поворот на 90 градусов вокруг вектора, совпадающего с крылечком
- Кручу-верчу, запутать хочу: углы Эйлера и Gimbal lock, http://habrahabr.ru/post/183116/, 23.06.2014
- Углы Эйлера, Википедия, http://ru.wikipedia.org/wiki/%D0%A3%D0%B3%D0%BB%D1%8B_%D0%AD%D0%B9%D0%BB%D0%B5%D1%80%D0%B0, 23.06.2014
- Maths — AxisAngle to Quaternion, http://www.euclideanspace.com/maths/geometry/rotations/conversions/angleToQuaternion/, 23.06.2014
- Вращение и кватернионы. Сборник рецептов, http://www.gamedev.ru/code/articles/?id=4215, 23.06.2014
- https://tinkercad.com/
Комментарии (10)

sbars
08.06.2022 20:37+5Учитывая, что крылечко не вектор, то какому-либо вектору тяжело будет "совпасть" с крылечком.
И ещё, поворачивая избушку вокруг оси, не проходящей через начало координат, Вам нужно задать эту ось - это какая либо точка на оси и вектор, коллинеарный этой оси. Для этого понадобятся два поворота, если мне не изменяет память. Т.е. два кватерниона.

FD4A
08.06.2022 23:05+1Ось и угол это хорошо, но я думал что (еденичный) квартерион это 4-х елементный ветор:
[v*sin(alpha/2) cos(alpha/2)], где v еденичный вектор направленный вдоль оси, а alpha это угол.

Zenitchik
08.06.2022 23:15+1А матрица поворота чем плоха?

Refridgerator
09.06.2022 07:08Отсутствием гарантированной консистентности (в силу избыточности данных) и дискретной направленностью. Возвести матрицу в нецелую степень, найти производную, посчитать длину пройденного пути будет не просто.

Zenitchik
09.06.2022 15:55Так для поворота кватернион тоже избыточен. Достаточно угла
в векторной форме.
Я чую, что всё удобство кватерниона должно быть в том, что он - число, а вектор или матрица - нет. Моя догадка верна?

Refridgerator
10.06.2022 05:49Кватернион тоже не число, а гиперкомплексное число — такая же математическая абстракция, как и матрица, в этом нет преимущества. Преимущества в аналитичности и одинаковой размерности — не нужно смешивать вектора и матрицы, не нужно использовать множество вариантов умножения (скалярное, векторное и т.д.). Недостатки — в большей сложности, векторы и матрицы интуитивно проще (и в школе их проходят, в отличие от).

Zenitchik
10.06.2022 15:28Кватернион тоже не число, а гиперкомплексное число — такая же математическая абстракция, как и матрица, в этом нет преимущества.
Отнюдь. Не такая же. Гиперкомплексные числа - это такая же абстракция, как действительные числа, но не такая же, как вектора или матрицы.
Преимущества в аналитичности и одинаковой размерности — не нужно смешивать вектора и матрицы, не нужно использовать множество вариантов умножения
Так это и есть следствие того, что кватернион - число, и на него распространены все операции с числовыми операндами и функции числовых аргументов.

Robgnokfar Автор
09.06.2022 19:26+2Господи, и 10 лет не прошло, а статья вышла!
Я писал эту статью в далёком 2014 году, кажется. Разбирался с тем, как задавать углы для сервомашинок робота в ROS и решил то, что понял выложить в виде статьи.
Сейчас конечно с улыбкой смотрю на эту пробу пера. Избушка - не совсем удачное объяснение. Лучше всего для математиков объясняет Савватеев.
А я тут попытался для программистов и робототехников, так сказать, с практической стороны.


Aquahawk
самое лучшее и понятное объяснение того что такое кватернион что я видел в жизни.