Привет, Хабр! Я Ани, отвечаю в Ozon Tech за обучение.
Сегодня поводом для поста на столь многоуважаемую аудиторию стал разбор задач контеста, который прошёл в рамках отбора участников на курсы Route 256.
Для справки: Route 256 — бесплатные курсы для мидл разработчиков от опытных инженеров Ozon Tech. В мае этого года мы запустили пять направлений: Go, QA, C#, iOS, Android. Это наш второй набор, сам проект стартовал осенью прошлого года.
Контест нам заменяет скрининг — мы проверяем технические навыки и опыт работы будущих участников, так как курсы рассчитаны на мидлов.
Ранее мы публиковали разбор задач по направлениям Go и QA (раз, два), пришло время поделиться задачами для C#, iOS (Swift) и Android (Kotlin, Java).
В этот раз нам посчастливилось провести контест совместно с Codeforces, и, судя по фидбеку участников, задачи зашли на ура. Надеюсь, разбор будет полезен и вам. А если захотите попробовать свои силы и попасть на курс, ищите ссылку на регистрацию ниже.

Задача «Сумма к оплате»
Дан массив цен за список продуктов, купленных в магазине. Товары с одинаковой стоимостью считаются одинаковыми.
Требуется посчитать, сколько потребуется заплатить суммарно за весь поход в магазин при условии, что в магазине проводится акция — «купи три одинаковых товара и заплати только за два».
Решение
План решения данной задачи можно сформулировать следующим образом:
Первым делом требуется посчитать количество товаров, имеющих одинаковую цену — обозначим эту величину для некоторой стоимости за
. Сделать это можно несколькими способами, самым простым из них является складывание всех цен товаров в структуру данных, предоставляющую быстрое изменение элемента и последующий проход по полученному контейнеру.
Примеры такого контейнера в разных языках программирования
Map в Kotlin, Dictionary в Swift, Dictionary в C#.
Также есть решение, требующее только константную дополнительную память и работающее быстрее на практике — отсортировать массив любой сортировкой и затем разбить получившийся массив на блоки одинаковых элементов линейным проходом.
Затем нам просто требуется посчитать , это и есть ответ.
Время работы и память
Асимптотика такого решения — где
— сумма количество купленных товаров по всем тестам, дополнительной памяти требуется линейное или константное количество в зависимости от реализации.
Разбор задачи «Электронная таблица»
Задана прямоугольная таблица из чисел. Требуется обработать
запросов: примените стабильную сортировку по неубыванию к столбцу
.
Требуется вывести таблицу после обработки всех запросов.
Решение
В данной задаче можно было сдать решение в лоб:
Первым делом считаем таблицу — будем хранить ее как массив , состоящий из массивов строк таблицы. Затем будем по порядку считывать запросы. Для каждого запроса (отсортировать столбец
) нам нужно применить стабильную сортировку к массиву
с компаратором, сравнивающим в
и
элемент с индексом
, то есть нам просто нужно использовать компаратор
.
Самое главное в этой задаче — придумать и написать правильно компаратор, а также знать стабильную сортировку из стандартной библиотеки или уметь писать ее самому.
Примеры стабильной сортировки в языках программирования
OrderBy в C#, sort() (начиная с Swift 5), sortedWith в Kotlin.
Время работы и память
В данной задаче проходили решения с любой разумной асимптотикой, но например решение описанное выше работает за .
Дополнительной памяти требуется константное количество.
Разбор задачи «Подсистема регистрации»
На вход подаются логинов, для каждого логина вам нужно сказать, можно ли его зарегистрировать. Логин должен соответствовать следующим правилам:
Логин — это последовательность из латинских букв в любом регистре, цифр и символов «_» или «-» (подчеркивание и дефис).
Логин не должен начинаться с дефиса.
Логин должен иметь длину от
до
символов.
Логины, которые отличаются только регистром, считаются одинаковыми.
Решение
Решение данной задачи состоит из двух основных идей:
Первая часть решения — проверка логина на первые три правила, это можно сделать либо напрямую проверить каждое из условий без использования регулярных выражений, либо с помощью регулярных выражений.
Регулярное выражение, рещающее задачу:
[0-9a-zA-Z_][0-9a-zA-Z_-]{1, 23}
Вторая часть решения — проверка логина, на то что раньше его еще не было. Для этого нам нужно привести логин в общий вид (например в нижний регистр), а затем использовать структуру, которая умеет быстро добавлять элемент и проверять элемент на наличие в множестве.
Подходящие структуры в разных языках
Set в C#, Set в Kotlin, Set в Swift.
Время работы и память
Асимптотика такого решения , дополнительной памяти требуется линейное количество.
Разбор задачи «Адресная книга»
Дается журнал звонков — набор записей (имя звонившего, телефон звонившего). Записи даны в хронологическом порядке от наиболее ранней к самой последней. Требуется восстановить для каждого звонившего 5 последних его номеров телефона.
Записи могут встречаться несколько раз, то есть возможна ситуация, когда одна пара (имя звонившего, телефон звонившего) встречается два и более раза во входных данных.
Решение
Заведем словарь из звонившего в очередь его номеров телефонов. Затем проходимся по набору всех записей. Для каждой записи проверяем, верно ли, что у звонившего в очереди уже есть этот номер телефона. Если это так, то просто удаляем его из очереди и кладем заново в конец очереди. Если же этого номера в очереди нет, то просто добавляем номер в очередь и в случае необходимости (число элементов в очереди больше 5) удаляем элемент из очереди.
В конце просто проходимся по словарю в лексикографическом порядке и выводим ответ.
Время работы и память
Время работы — , где
— сумма количеств записей по всем тестам, такое время работы обуславливается тем, что очередь у нас всегда размера не более 5, а следовательно все операции с ней работают за константное время.
Дополнительная память в данном случае будет линейной.
Разбор задачи «Система продажи билетов на поезда»
Есть купе, пронумерованных от
до
, в каждом купе два места, поступают запросы трех видов:
Занять место, если оно еще не занято.
Освободить место, если оно занято.
Занять купе с наименьшим номером, в котором все места свободны.
Если в купе освободили все места — то оно также считается свободным.
Решение
Собственно решим задачу сначала только для обычных мест (без купе). Для решения этой задачи давайте заведем словарь для мест — где для каждого места запомним свободно оно или нет. Для первого запроса мы просто проверим занято место и если нет, пометим занятым. Для второго же запроса мы наоборот проверим занято ли место и если да, пометим его незанятым.
Для обработки купе заведем структуру, которая позволяет удалять произвольный элемент, находить минимальный элемент и вставлять — по таким критериям подходит любое балансирующее дерево или правильная куча, поддерживающая удаление произвольного элемента.
Пример подходящей структуры
SortedSet в C#, sortedSetOf в Kotlin.
На запросы третьего типа мы теперь просто ищем минимум в нашей структуре и помечаем места в словаре занятыми. Также теперь нам требуется дополнительно реализовать в запросах первого и второго типа обработку проверки: забронировали купе или его освободили (это можно делать даже в наивную просто проверяя оба места из купе).
Время работы и памяти
Для каждого запроса мы требуем времени (поиск/удаление/вставка в выбранную нами структуру или словарь), итого суммарное время работы —
, где
— суммарное количество запросов.
Также нам требуется дополнительной памяти для хранения всех мест и всех купе.
Разбор задачи «Многомодульный проект»
Есть модулей, для каждого известны зависимости, которые нужны для его установки. Есть
запросов — на каждой запрос нужно установить какой-то модуль, предварительно поставив все его зависимости, игнорируя уже установленные модули.
Решение
Для решения этой задачи нужно было составить для каждого модуля список его зависимостей.
Рисунок связей для первого теста из условия:
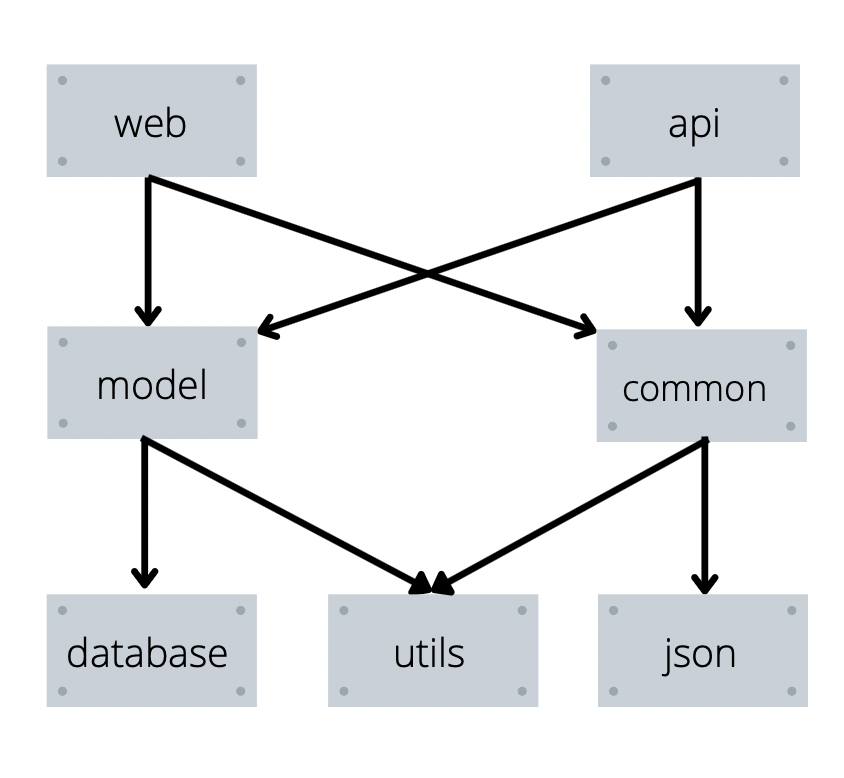
Затем на запрос установки модуля запустим функцию, которая для каждого модуля проверяет были ли установлены все его зависимости и если нет, то поочередно будет запускаться из его зависимостей, до тех пор пока не установит все зависимости модуля.
Например, когда на рисунке выше вызывается установка модуля web, то наша функция сначала попытается установить model, установит для нее database и utils, а затем точно также попробует установить commons и получит нужный порядок установки.
Пример работы функции в рисунках
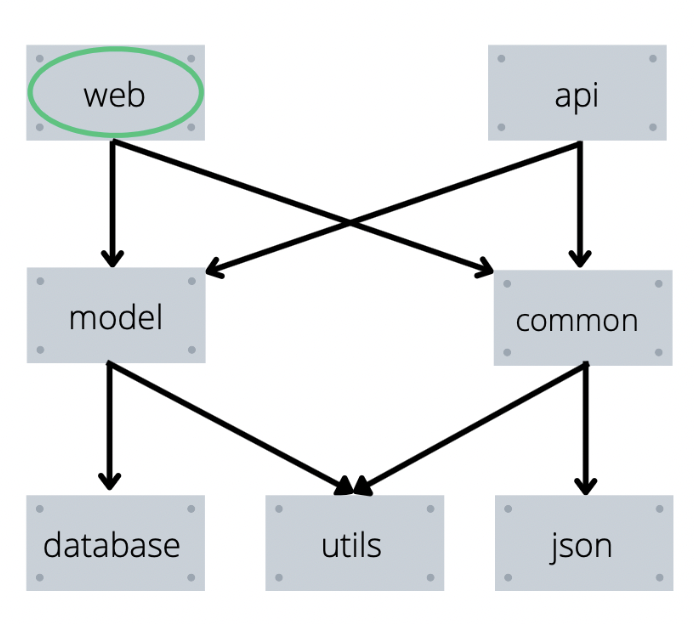
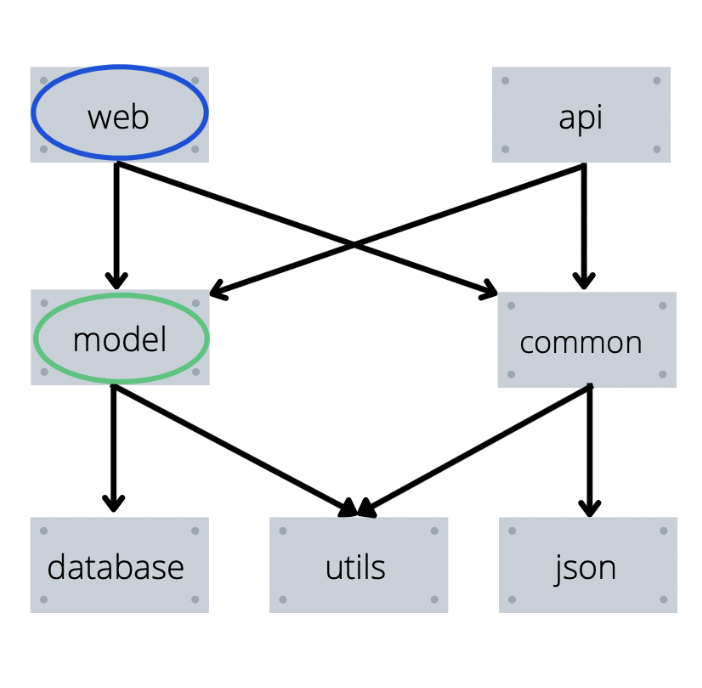
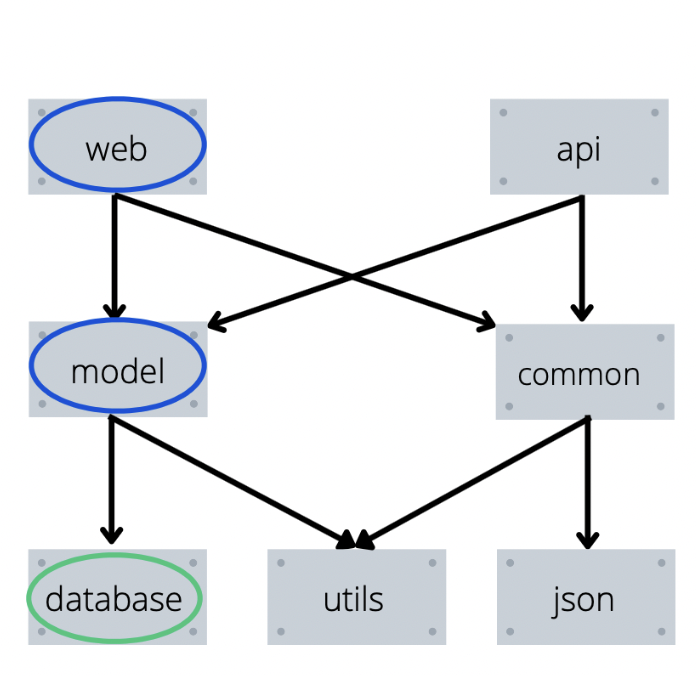
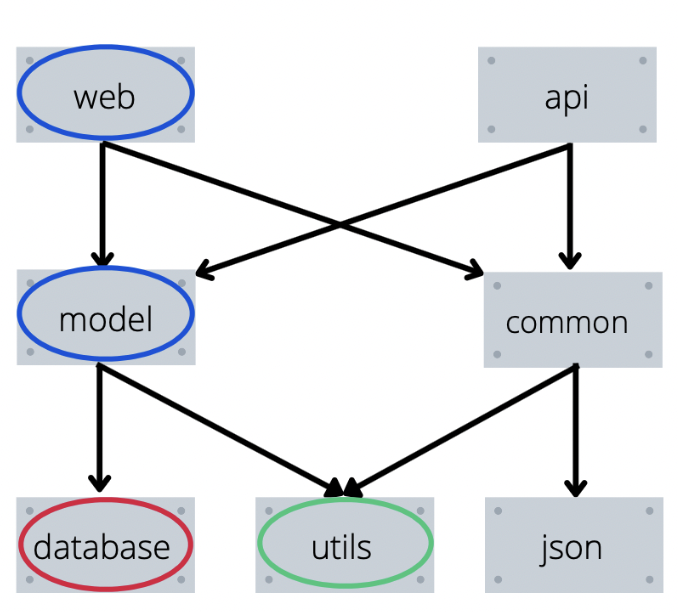
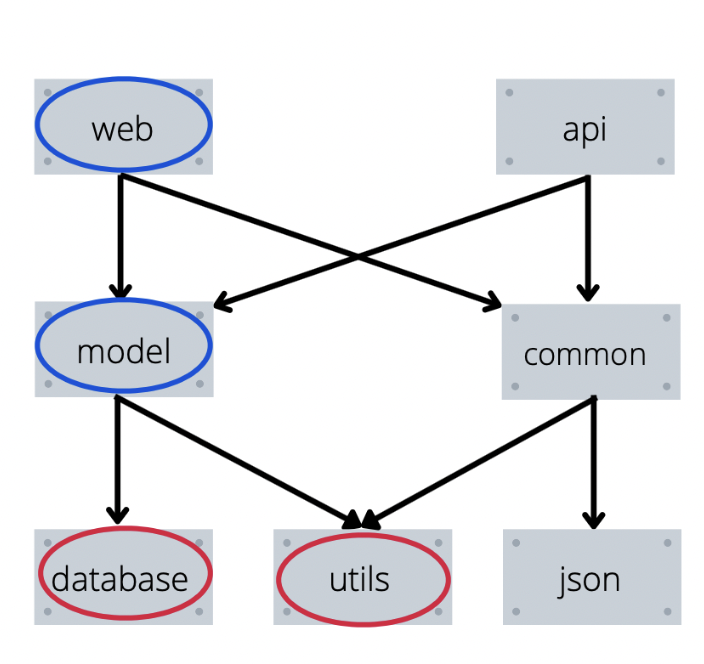
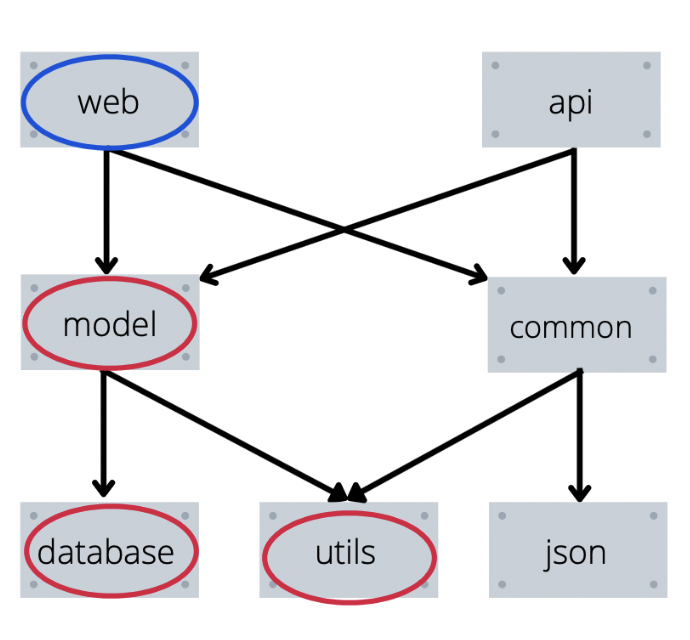

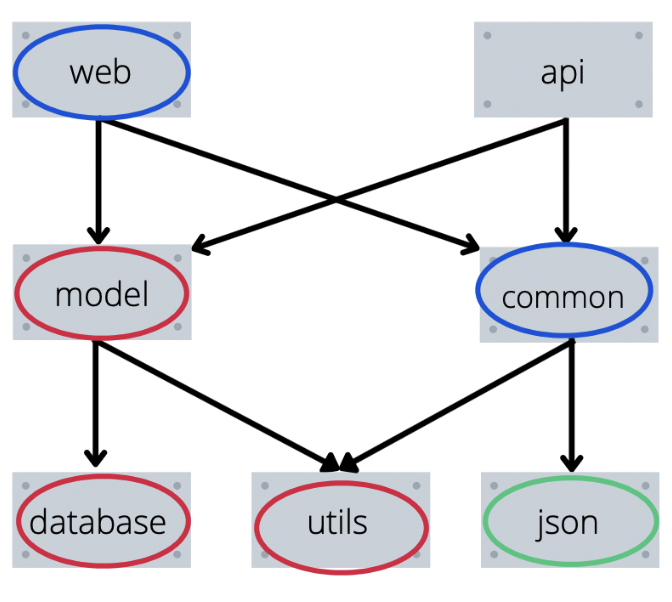
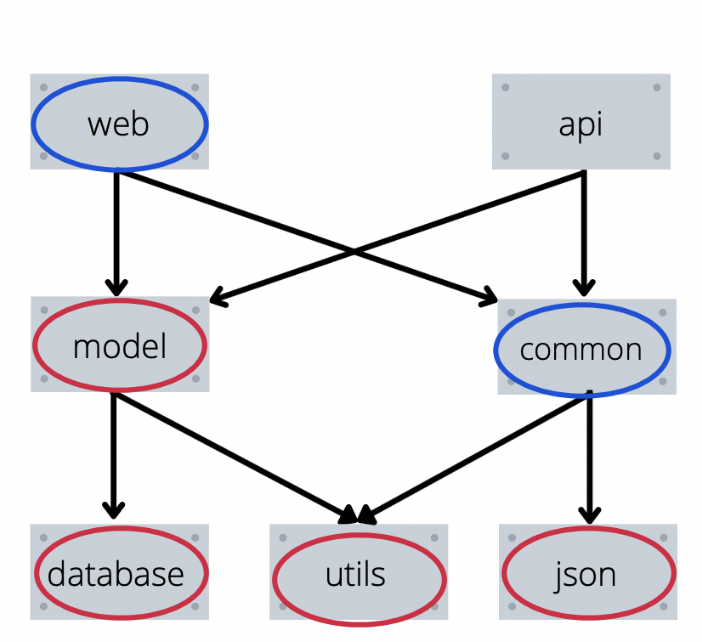
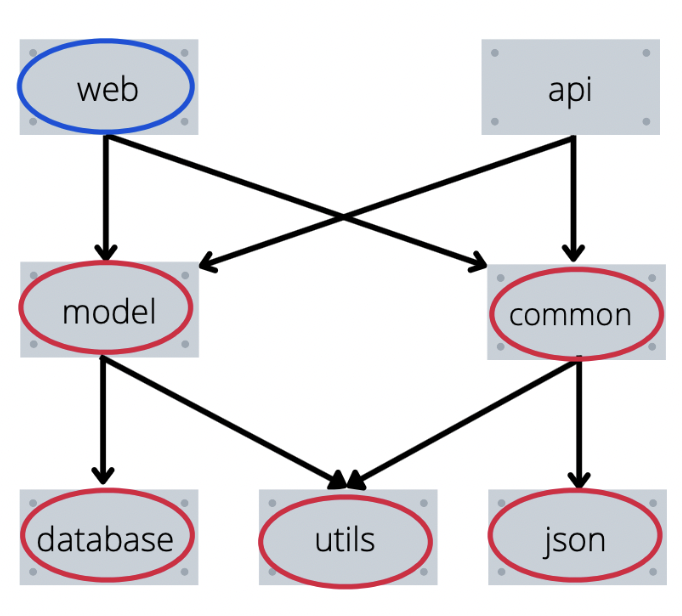
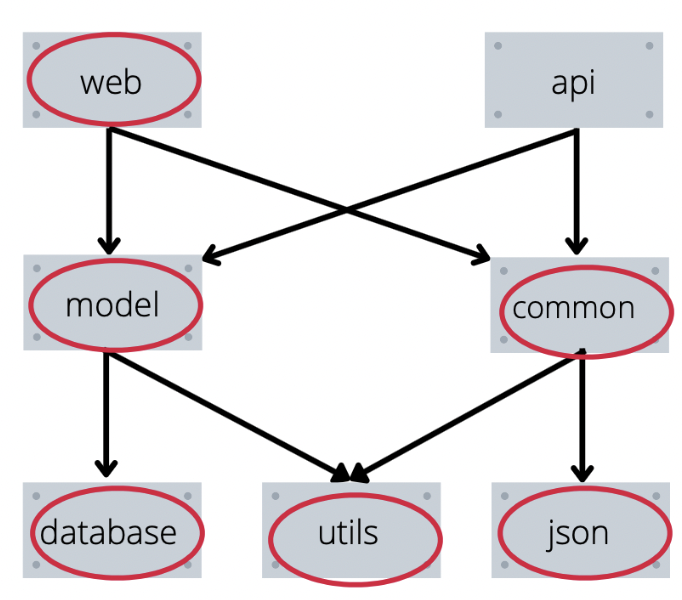
Пояснение к рисункам выше:
Красным будет выделен элемент, который мы уже установили.
Синим — элемент который мы пытались установить, но перешли в его зависимости.
Зеленым — элемент который мы пытаемся установить сейчас.
Не выделены цветом — элементы, которые мы вообще не трогали.
На самом деле такое решение называется топологической сортировкой.
Время работы и памяти
Каждый модуль мы не можем установить более 1 раза, а также каждую зависимость мы не можем посмотреть более 1 раза на каждый запрос. А следовательно наше решение работает за .
Дополнительная память требуется только для рекурсии, которая в худшем случае просто обойдет все модули, а следовательно нам требуется не более дополнительной памяти.
Разбор задачи «Г-образный морской бой»
Есть поле , некоторые клетки свободны, они обозначаются символом «.», а некоторые заняты — «*». Корабль — Г-образная фигура размера 1, 3, 5 или 7 точек.
Ниже можно видеть все примеры кораблей:
... .... ..... ......
.*. .**. .***. .****.
... .*.. .*... .*....
.... .*... .*....
..... .*....
......
Корабли можно вращать
Требуется проверить может ли поле, данное в тесте, быть полем для морского боя, при условии правильного размещения кораблей (корабли не должны прикасаться ни по горизонтали, ни по вертикали, ни по диагонали).
Решение
Данная задача — задача в основном на реализацию, так как требуется просто реализовать, то что спрашивается в условии — то есть просто проходить по полю и явно убирать корабли, если они размещены правильно. Но есть несколько способов упростить себе решение:
Первым делом для проверки, правильно ли размещён корабль, можно использовать шаблоны: сделать 4 шаблона для каждого из кораблей. Для проверки «верно ли, что в этой позиции находится корабль» — нам просто нужно проверять, подходит ли кусочек поля под шаблон. При сравнении по шаблону нам нужно считать, что элементы за границами поля при сравнении считаются пустыми ячейками.
... .... ..... ......
.*. .**. .***. .****.
... .*.. .*... .*....
...X .*.XX .*.XXX
...XX .*.XXX
...XXX
X — любой символ.2. Так как корабли можно вращать, то нужно было сделать не 4 шаблона, а целых 16, но так как в шаблонах было бы легко запутаться, то можно просто написать функцию rotate, которая будет вращать шаблон на 90 градусов и таким образом получить все нужные нам шаблоны.
Пример работы такого алгоритма
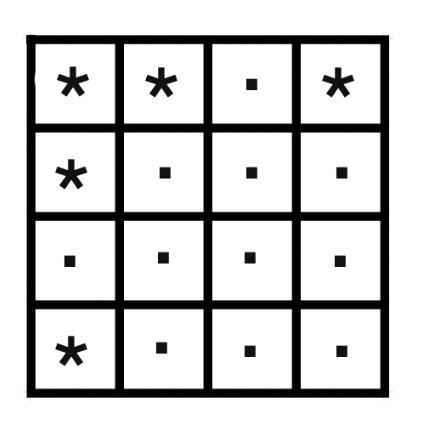
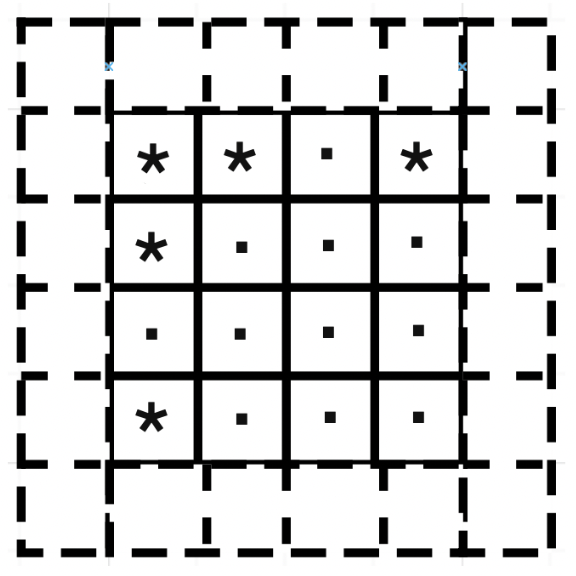
Начнем с клетки (0, 0) — там будет стоять звёздочка, далее:
Будем по очереди проверять все шаблоны.
Когда дойдем до шаблона размера 2, увидим, что он нам подходит, так как клетки (-1, -1), (-1, 0), (-1, 1), (-1, 2), (0, -1), (0, -2) находятся за границей и считаются в нашем алгоритме свободными.
Удалим корабль с центром в точке (0, 0).
Продолжим алгоритм.
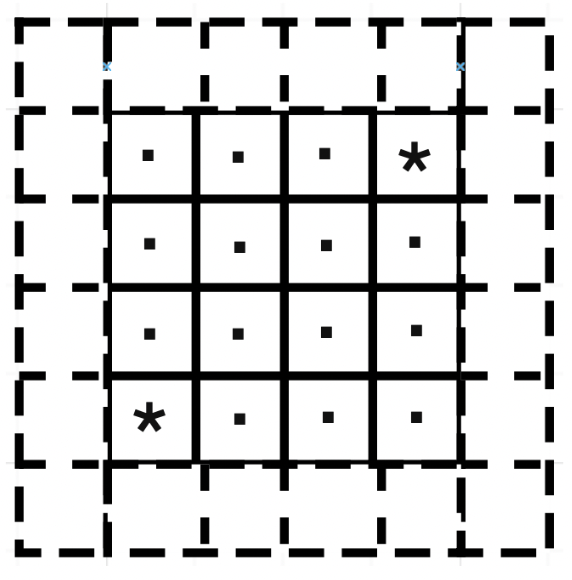
Затем проверим клетку (0, 3) — найдём подходящий шаблон и удалим корабль, также проверим клетку (3, 0) — в результате получим пустое поле. Так что изначальное поле было полем для морского боя.
Время работы и памяти
Так как в каждую клеточку поля мы пытаемся подставить корабль, напрямую проверяя кусок поля с шаблоном, то данное решение будет требовать , где
— размер шаблона,
— количество шаблонов. Так как
и
— константы, то в итоге мы получили решение за
.
Дополнительной памяти же нам достаточно , то есть константное число дополнительной памяти.
Такими были задачи для поступления на курсы:
Если вы нашли более изящное решение — делитесь в комментариях:)
Комментарии (4)

paranoik
14.06.2022 21:38Г-образный морской бой:
Бежим по полю ищем звёздочку. Если встречаем, заменяем ее на что-то другое (на x) чтобы не зациклилось, рекурсивно проверяем и заменяем соседние, ищем минимальную и максимальную координаты. Получаем левый верхний и правый нижний угол поля, содержащего корабль. Анализируем, можно сравнить с шаблонами, можно аналитически - это квадрат, кол-во символов корабля (1,3,5,7) и их взаимную симметрию.

BellaLugoshi
15.06.2022 09:58Пардон, я не привыкший решать задачки, но с Морским боем у меня непонятки уже на этапе условий задачи (какое-то "это" поле например), я конечно почитал решение и понял о чем там речь, но написать нужно было так:
Дано поле M*N с уже размещенными кораблями, где символом "точка" отмечаются пустые ячейки, а символом "звезда" элементы корабля. Нужно проверить - являются ли все расставленные корабли соответствующими набору "Г"-образных кораблей и соблюдаются ли условия взаимного размещения - на соседних ячейках разных кораблей не должно быть ячеек "звезда" ни по горизонтали, ни по вертикали, ни по диагонали.
Так же в условии ничего не сказано про границу поля. Видимо граница может соприкасаться с кораблём. Но в примерах кораблей и затем в шаблонах явно указана невозможность соприкасания с границей поля.
Касательно решения - так как шаблоны друг от друга отличаются, но и подобранный шаблон будет блокировать часть поля как одобренную (ну или прерываться если будет нарушено хотя бы одно условие). Отсюда потребуется хранить информацию о всё еще непроверенных ячейках.
Я бы предложил такое решение:
Делаем проход по M*N и проверяем на такие основные признаки:
а) ищем корабли 1х1
... .*. ...б) ищем шаблоны для возможных частей кораблей
.*. ... ... .*. .** .** **. **. ... .*. .*. ...Сохраняем информацию и найденных шаблонах в виде координат центральной точки. Дальнейшие проверки делаем отталкиваясь от них.
Я с шаблонами работал ранее и мне понравилась линейная схема хранения шаблонов, например шаблон
... .*. ...хранится как
{{-1, -1}, {0, -1}, {1, -1}, {-1, 0}, {0, 0}, {1, 0}, {-1, 1}, {0, 1}, {1, 1}}Тут за опорную точку взят центральный сектор, это если привязываться к тому, что я описал выше, в целом можно привязаться к любой точке, но именно здесь удобно это делать на сектор, который есть во всех шаблонах и является центром вращения.

TiesP
15.06.2022 10:02Адресная книгаХраним найденные телефоны в словаре словарей.
Основная идея в том, чтобы идти с конца, поэтому мы не будем перезаписывать уже найденные телефоны.
Также пользуемся тем, что `dict` в python сохраняет порядок, в котором он заполнялся.
Поэтому для получения правильного списка телефонов нам нужно будет всего лишь перевернуть найденный список телефонов.def restore_5_last_phone(arr): log = defaultdict(dict) for name, phone in arr[::-1]: if len(log[name]) < 5: if phone not in log[name]: log[name][phone] = True # выводим имена в алфавитном порядке, # также для списка телефонов делаем reverse, поскольку мы записывали с конца for name in sorted(log): print(name, ' '.join(list(log[name])[::-1])) """ Пример ввода 10 b 222 a 777 a 333 a 111 a 111 b 111 a 333 a 666 a 444 a 555 Пример вывода a 111 333 666 444 555 b 222 111 """


TiesP
Извиняюсь что на python :) Использую только стандартные библиотеки… И только изящные решения)
Транспонируем матрицу. Запоминаем, какие колонки сортировали.
Таким образом сложность решения будет максимальное из O(n * m) и O(uniq(k) * n log n), где uniq(k) — это кол-во уникальных колонок для сортировки.
… остальные пока не решал