Переработал первоначальное оформление статьи по советам администраторов сайта. Им спасибо. Надеюсь текст стал понятнее.

Описание гипотезы Коллатца в вики: https://ru.wikipedia.org/wiki/Гипотеза_Коллатца
цитирую : Берём любое натуральное число N. Если оно чётное, то делим его на 2,
а если нечётное, то умножаем на 3 и прибавляем 1 (получаем 3*N + 1).
Над полученным числом выполняем те же самые действия, и так далее.
Гипотеза Коллатца заключается в том, что какое бы начальное число N мы ни взяли, рано или поздно мы получим единицу.

Попробуем сделать шаг в сторону и исследовать преобразование с вычитанием 1,
то есть умножаем на 3 и вычитаем 1 (получаем 3*N - 1).
Результат делим на 2 до нечетного значения и так далее. Результат с вычитанием 1 состоит в том, что есть несколько точек остановки алгоритма, а не только единица. Примеры на картинках ниже.

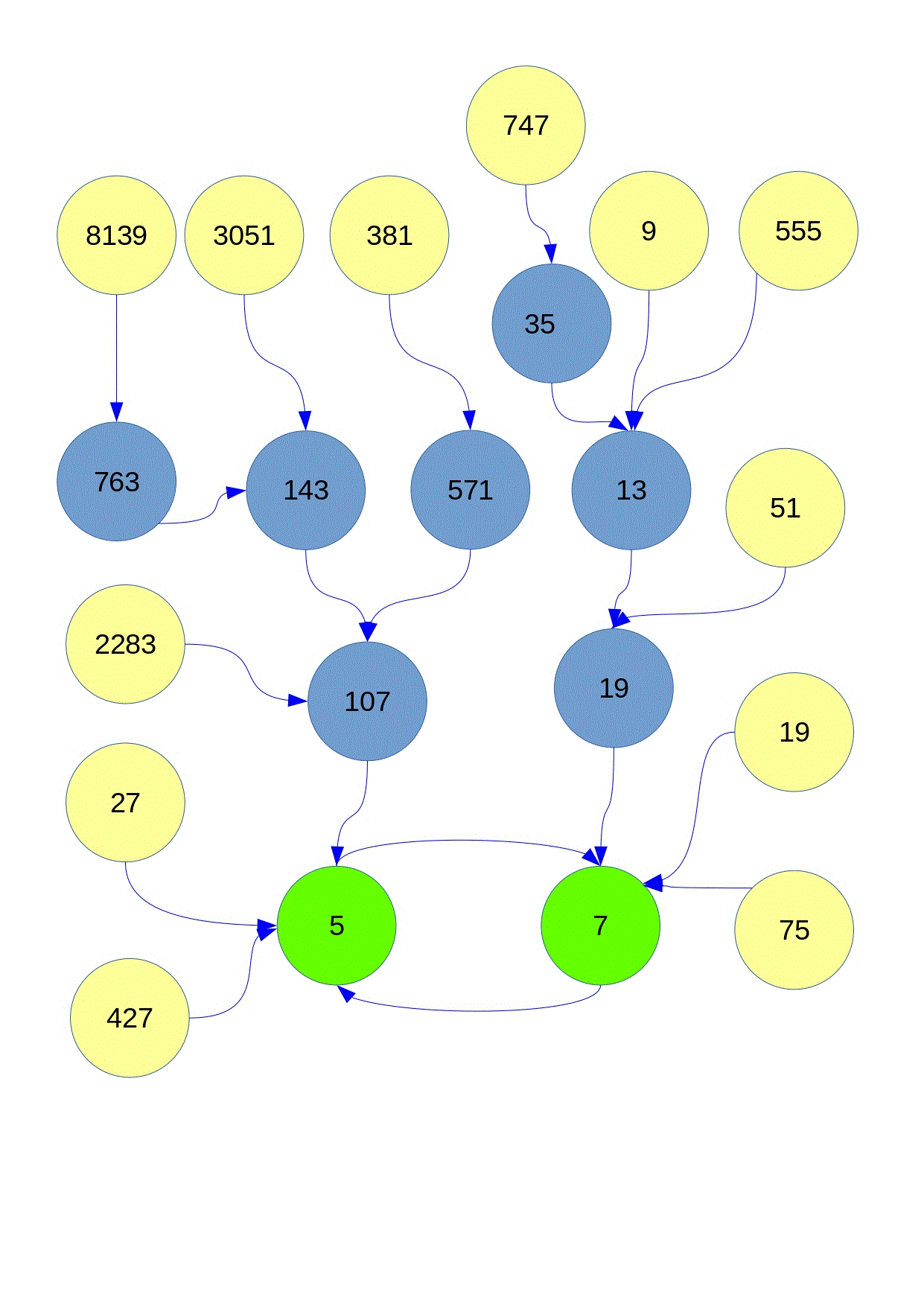
Терминальные числа выделены зеленым. Числа кратные 3 желтым. Числа кратные 3 могут быть только первыми в цепочке преобразований. ( Это относится и к обычному преобразованию Коллатца с добавлением 1 ). Все остальные числа выделены синим.

Возможно существуют еще замкнутые цепочки, но я их не обнаружил.
Существуют достаточно длинные цепочки, например:
153 -> 229 -> 343 -> 257 -> 385 -> 577 -> 865 -> 1297 -> 1945 -> 2917 -> 4375 -> 3281 -> 4921 -> 7381 -> 11071 -> 8303 -> 6227 -> 2335
-> 1751 -> 1313 -> 1969 -> 2953 -> 4429 -> 6643 -> 2491 -> 467 -> 175 -> 131 -> 49 -> 73 -> 109 -> 163 -> 61

Вопрос о том, что для любого нечетного числа, для преобразование 3*N - 1, мы имеем только 3 варианта остановки, или есть еще остановки, или есть возможность алгоритма не завершится за конечное число шагов мне неизвестен.