Антипаттерны в написании учебных пособий или откуда растут ноги плохого кода? / forpes.ru

Главная
Антипаттерны в написании учебных пособий или откуда растут ноги плохого кода?

Антипаттерны в написании учебных пособий или откуда растут ноги плохого кода? +20

25.06.2022 00:18

sepetov 53 9500 Источник

Работа с плохим кодом лично у меня вызывает отвращение и — по правде говоря — ещё и неприличные мысли в отношении того, кто его писал. Сейчас я уверен, что кроме программистов проблему плохого написания по-настоящему не понимает никто, хотя эта проблема есть не только у нас. В этой статье я покажу это на примере учебных пособий по математике. Не в них ли рождается склонность к отвратительному коду, ведь математику проходили все?

Статья будет полезна разработчикам, которым пришло распоряжение написать документацию к ПО, а также авторам учебных пособий вузов. Я не питаю иллюзий, что ситуация как-то изменится что у первых, что у вторых, но помечтать всё же хочется.

Важно: пример из статьи не является вымыслом или шуткой!

Ещё важней: статья не является критикой математики, математику я люблю.

Давайте сразу к делу: проанализируем первое попавшееся в поисковике решение квадратного уравнения на листочке.

Источник: https://hotcore.info/algebra/298548

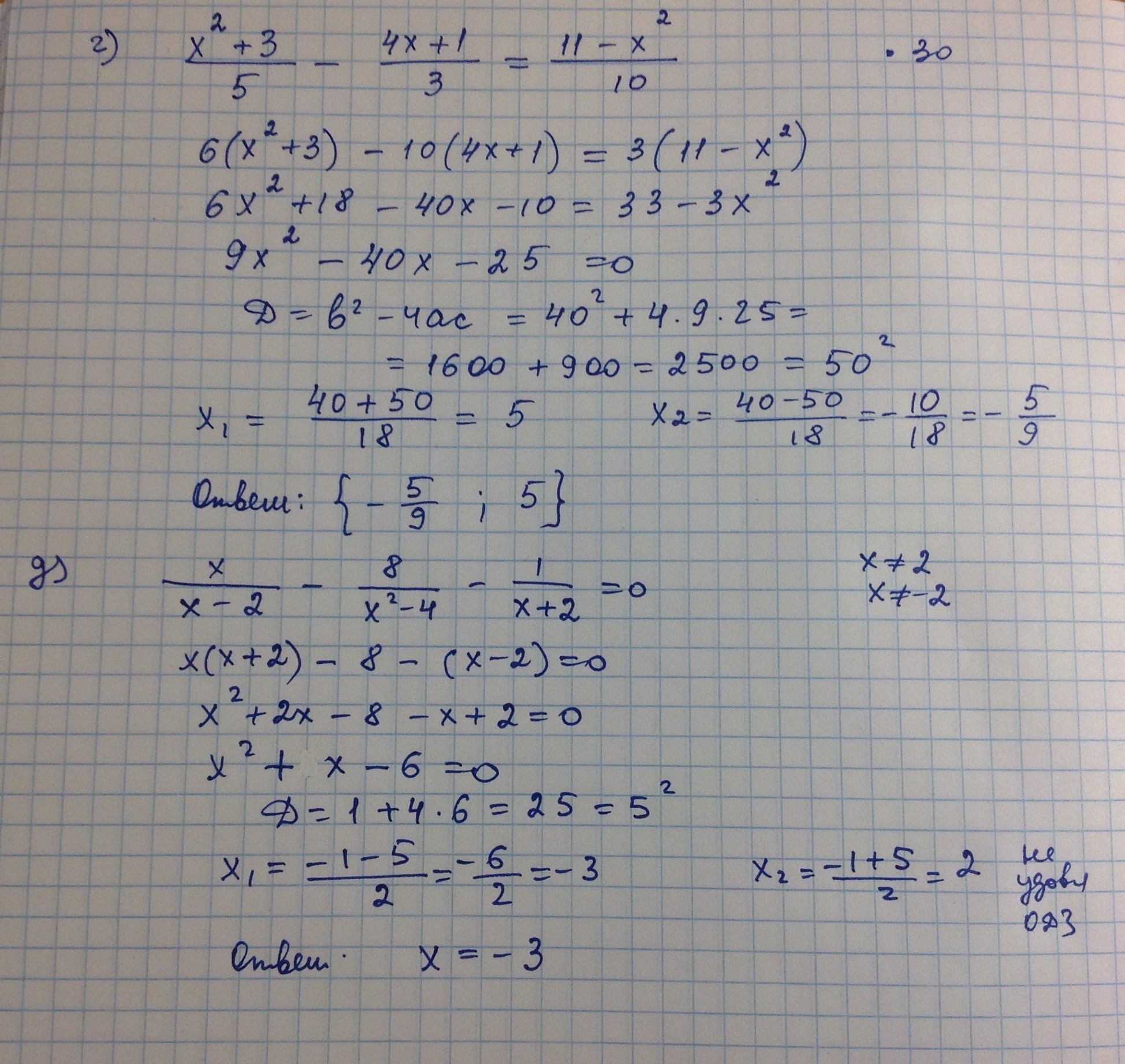
Уже на таком простом примере видно, что для таких решений характерно следующее:

это сложно тестировать
низкая наглядность — сплошная простыня символов, которая будет нечитабельной при большом объеме
сложно разбить на маленькие ~~функции~~ блоки из которых итоговый алгоритм можно было бы собрать как из «кирпичиков»
если закралась ошибка/опечатка — её тяжело найти.

В основном это минусы не математики, а бумажного носителя, но вишенкой на торте всё же являются переменные. В математике имена переменных всегда из одной буквы, часто используются нижние индексы: x₁, x₂, …, x_n, за что в среде программистов, напротив, применяют самые жёсткие санкции. В примере выше переменных не так много, но какая чехарда начинается в более крупных примерах? Большинство решений представляют собой длинный ~~код~~ шифрованный текст. Без раздумий никто не скажет, чем x₄ важней x₇ и что содержит каждая из них. Оппоненты возражают: индексированные переменные не требуют различий между собой, а в сложных решениях сквозную нумерацию индексов для всего решения вообще никто не применяет. Хорошо, а что тогда хранится в условной переменной b_m и как она связана с условной h?

Проблема может показаться не такой серьёзной, поэтому выход из неё ищут редко. В случае с математикой и физикой это осложняется математической нотацией, уже ставшей традиционной несмотря на неудобство. Она выполняет роль легаси-кода, который разрабатывался очень долгое время, совершенно разными людьми и даже разными поколениями. Идеи отказа от старой математической нотации и разработки новой существуют давно, но ни одна так и не взлетела.

А теперь краткое содержание этой статьи одним абзацем: здесь приведены два варианта оформления математического упражнения, где «хороший» вариант наглядней и примерно в 160 раз короче «плохого», хотя и там и там был идентичный алгоритм. Плохой пример навеян увиденной методичкой для студентов некоего тюменского вуза. Статья написана после того, как я спустя почти 15 лет столкнулся с похожей в одном из екатеринбургских…

Плохой вариант является фантастическим антипаттерном и, к сожалению, он всё-таки из жизни, а не искусственно придуман «шутки для». На текущий момент это самая плохая публикация, которую я видел в печати.

Методичка, кстати, получилась такой по очень грустной и банальной причине.

Скорее всего это болезнь. Преподаватель с весьма специфическим характером, на который наложились сильные возрастные изменения психики, решил снова заняться сочинением и публикацией своих трудов. Получилось не очень. Обидно осознавать, что подобные недуги до сих пор являются неизлечимыми. Ещё страшней от того, что такое же может грозить каждому из нас. Увы, с возрастом интеллект часто снижается, но прошлые достижения и публикации от этого никуда не деваются, что даёт формальное основание считать такого сотрудника полезным за его прошлые способности.

Как такие сочинения проходят рецензию и поступают в тираж вуза — печальная тема, которую я затрагивать не буду.

Я знаю, что формулы почти никто не читает и даже есть утверждение: каждая формула уменьшает количество читателей вдвое. Поэтому я спрятал оба решения под спойлеры. Для понимания статьи нет необходимости читать оба примера от буквы до буквы, но желателен хотя бы беглый просмотр. Намекну, что формулы есть только в первом решении, а второе приведено в крайне сокращённом виде и без них. Знайте, что прочтение содержимого спойлеров сделает вашу совесть чистой и шелковистой!

В конце статьи приведена таблица сравнения учебной литературы с программированием.

Пример короткий, пример хороший

Упражнение: найти первообразную функции:

$\int ln(x) \cdot (3x + 2) \mathrm{d} x$

Решение

Для краткости весь этот интеграл мы так и будем называть — y. Самое простое решение — это интегрирование по частям. Для тех, кто забыл или не знал, что это такое — это формула производной от произведения, только наоборот. В школе мы писали её так:

$(U \cdot V)^{'} = U^{'} \cdot V + U \cdot V^{'}$

Если проинтегрировать левую и правую части этого равенства, то будет уже готовая формула интегрирования по частям (хотя пишут её чуть-чуть в другом виде):

$U \cdot V = \int U^{'} \cdot V + \int U \cdot V^{'}$

Оба интеграла в правой части у неё очень похожи структурой на интеграл у: они тоже состоят из двух сомножителей. Поэтому можно подставить y вместо любого и них и формула станет короче. Либо так:

$U \cdot V = у + \int U \cdot V^{'}$

Либо так:

$U \cdot V = \int U^{'} \cdot V + у$

Какой вариант выбрать и как? Опытным путём. Конечная цель — это чтобы второй из оставшихся интегралов был проще, чем исходный y (принцип: «упрощаем сложное»). Сравним оба варианта подстановки. Первый:

$y = \int U^{'} \cdot V \implies \left [ \begin{array}{c} U^{'} = \ln( x ) \\ V = ( 3 \cdot x + 2 ) \end{array} \right ]$ $y = \int U \cdot V^{'} \implies \left [ \begin{array}{c} U = \ln( x ) \\ V^{'} = ( 3 \cdot x + 2 ) \end{array} \right ]$

Лично мне бросается в глаза то, что в первом варианте прямо сейчас придётся искать интеграл от логарифма, что легко, но всё же сложней, чем не искать его вовсе. Поэтому рискнём остановиться на втором варианте, избавимся от знака производной в его комментарии и посмотрим, что получится:

$V^{'} = ( 3 \cdot x + 2 ) \implies V = 3 \cdot \frac{x^{2}}{2} + 2 \cdot x$

Теперь вернёмся к формуле интегрирования по частям и подставим в неё этот комментарий:

$\begin{array}{c} U \cdot V = \int U^{'} \cdot V + y \implies \\ \ln(x) \cdot ( 3 \cdot \frac{x^{2}}{2} + 2 \cdot x ) = \int \frac{1}{x} \cdot (3 \cdot \frac{x^{2}}{2} + 2 \cdot x) \mathrm{d} x + y \end{array}$

Выражаясь нехорошим языком, здесь уже многабукф. Это выражение действительно более громоздкое, чем исходный y, но единственный оставшийся интеграл более простой. Поэтому вместо сложного короткого примера у нас теперь простой длинный, который можно сделать ещё проще и ещё длинней. Делаем это в три действия:

перенесём y в одну сторону, а всё остальное — в другую
раскроем скобки внутри оставшегося интеграла
решим наконец этот последний интеграл

Итак, первое:

$y = \ln(x)( 3 \cdot \frac{x^{2}}{2} + 2 \cdot x ) - \int { \frac{1}{x} \cdot (3 \frac{x^{2}}{2} + 2 \cdot x)} \mathrm{d}x$

Теперь второе:

$y = \ln(x) \cdot ( 3 \cdot \frac{x^{2}}{2} + 2 \cdot x ) - \int 3 \cdot \frac{x}{2} + 2 \mathrm{d} x$

Наконец, третье:

$y = \ln(x) \cdot ( 3 \cdot \frac{x^{2}}{2} + 2 \cdot x ) - \frac{3}{2} \frac{x^{2}}{2} - 2 \cdot x$

Вот и ответ (плюс константа).

Резюме: написанное мной решение уместилось (почти) на страницу А4. Возьмём эту версию решения как образец, с которым будем сравнивать следующий пример.

Пример длинный, пример плохой

Жаль, но копипастить его нельзя. Признаюсь, что я добросовестно пытался написать с нуля точно такую же методичку, но, видимо, моя фантазия не имеет такого же диагноза. Приведу часть оглавления и несколько характерных фрагментов — вы очень скоро согласитесь, что этого будет достаточно.

Здесь нечто!

Том (!) первый, введение, отрывок:

В современном мире не ~~только лишь~~ все могут осознанно воспринимать возложенные на них обязанности, что негативно сказывается на процессе коммуникации более старшего инициатора, являющегося A posteriori ответственным за постановку задачи, и исполнительным субъектом, который Actum ut supra осуществит подконтрольные действия в форме, пригодной для вышестоящей оценки.

Солидное начало? Это для упражнения, в котором условие умещается в 60 символов и меньше 20 символов в уравнении! Идём дальше — отрывок темы 3.2.2.1.2.3 параграфа 3.2.2.1.2 главы 3.2.2.1 части 3.2.2 раздела 3.2 третьего тома:

...Полученная формула является следствием формулы А, рассмотренной нами ранее в теме 2.3.2.1.1.4 параграфа 2.3.2.1.1 главы 2.3.2.1 части 2.3.2 раздела 2.3 второго тома, путём подстановки вместо второго слагаемого правой части выражения, приведённого в теме 1.1.1.2.1.1 параграфа 1.1.1.2.1 главы 1.1.1.2 части 1.1.1 раздела 1.1 первого тома с учётом преобразований, выполненных в теме 2.1.1.1.1.2 параграфа 2.1.1.1.1 главы 2.1.1.1 части 2.1.1 раздела 2.1 второго тома. …

Описанный нами результат мы будем использовать при получении ответа в будущей теме 3.1.1.1.1.1 параграфа 3.1.1.1.1 главы 3.1.1.1 части 3.1.1 раздела 3.1 этого тома.

На этом можно было бы закончить цитирование, но для тех, кому мало, я припрятал примерно воспроизведённое мной оглавление (с сокращениями!), которое фигурировало в первоисточнике. Обратите внимание на то, что индексы в оглавлении почти никогда не превышают единицу, ведь в каждой теме/параграфе/главе в основном одно-два предложения, которые и так исчерпывающе их описывают, что развить мысль, дописав что-то новое просто невозможно. Ближе к концу оглавления этот эффект «единичности нумерации» только усиливается.

Примерно таким является оглавление, не судите за сумбурность пересказа

Том 1. Проблематика формулирования рассматриваемого проекта решения.
Введение
Раздел 1. Математические выражения — основа описательной части передаваемой на исполнение работы
Часть 1. Уравнения
Глава 1. Линейные уравнения
Глава 2. Квадратные уравнения
Часть 2. Преобразование выражений
Глава 1. Элементарные арифметические преобразования
Параграф 1. Раскрытие скобок
Тема 1. Перестановка слагаемых
Параграф 2. Умножение уравнения на константу
Часть 3. Системы уравнений
Глава 1. Системы линейных алгебраических уравнений
Раздел 1.2. Представительность решений, стандартизация практик и оформления сопроводительной документации
Часть 1.1.1. Графическое представление документации
Глава 1.1. Графики функций
Параграф 1.1.1. Точки перегиба.
Часть 1.2. Сопроводительная литература и информационные источники
Глава 1.1. Выбор авторитетных источников литературы

Том 2. Интегральное и дифференциальное исчисление.
Введение
Раздел 2.1. Дифференцирование математических выражений и доступный математический аппарат
Часть 1. Таблица производных
Глава 1. Производные от алгебраических функций
Глава 2. Производные от тригонометрических функций
Часть 2. Дифференцирование сложных выражений
Раздел 2. Интегрирование функций и теоретико-методический комплекс приёмов интегральных вычислений
Часть 1. Таблица интегралов
Часть 2. Неалгоритмические особенности вычисления интегралов
Раздел 3. Взаимосвязь дифференцирования выражений и интегрирования функций
Часть 1. Интегрирование по частям

Том 3. Рационализация математического инструментария
Введение
Раздел 1. Точки внимания
Часть 1. Трудновыполнимые вычисления в интегралах
Раздел 2. Стратегия последовательных выборов хода решения
Часть 1. Временные затраты на вычисления выражений
...

Теперь давайте сравним оба решения

В первом решении 11 формул, незначительные упущения, есть пояснения и... всего 263 слова. Во втором — три тома, в каждом из которых около 80 страниц формата А5. В среднем на странице умещается 180 слов на русском языке. Итого: около 43 тысяч слов и уже неустановленное число формул.

Если провести аналогию первого решения с листингом программы, то в нём одно подключение внешней библиотеки, 7 строчек присвоения и один if … else. Комментарии, на мой взгляд, многословны, но по характеру хотя бы разделены на те, которые показывают:

что делает этот «код»
почему именно такой ход мысли

В решении нет ничего похожего на циклы, многочисленные зависимости, операторы goto и т. п. — оно примитивное и последовательное. Большинство предложений — короткие, очень мало вводных конструкций, деепричастных оборотов и вот этого вот всего.

Второе же решение оформлено его автором как целый курс. Это не тот масштаб для решения одного упражнения!

Что именно (чисто технически) делает второй пример таким плохим? Целый ворох «особенностей»:

большое оглавление
перегруженное оглавление
перенасыщенная детализация оглавления
многословность оглавления (да, именно так — переменные в уравнениях делаем однобуквенными, а в оглавлении отрываемся по полной)
абстрактно сформулированные пункты оглавления
иногда непоследовательное содержание
бесконечные ссылки на «туда» и «там»

В решении много «сервисного» содержимого, бессодержательные комментарии, перекрёстные ссылки (аналог goto). За таким объёмом данных не видно само упражнение. Вы уже сами отчётливо представили, что каждая страница такой методички в основном состоит из предложений, содержащих одни и те же слова, которые даже не пересекаются с математикой вообще и этим упражнением в частности.

А вот с точки зрения автора написанное пособие идеально — в нём всё досконально разложено по полочкам, а несмотря на обилие повторяющихся фраз «как было написано ...», «как было уже сказано ...» и пр., ни в одном параграфе нет повторяющейся информации. Почти каждая новая мысль хронологически выстроена верно и нет ни одной логической ошибки. Ветвистое оглавление имеет непротиворечивую (почти) структуру.

Как это связано с плохим кодом?

Плохим влиянием. Решение не только не полезно, но и вредно — оно отнимет у учащегося время и опыт, который он мог бы получить с другой методичкой, которая, кстати, есть в этой же библиотеке. Также у человека формируется ощущение «нормальности» плохого способа изложения, из-за чего вредный стиль может частично перейти в привычку и затем вылиться на первом же месте работы в виде плохого кода.

Вы замечали, как некоторые начинающие разработчики защищают свой первый код во время ревью? Это тоже является следствием обильной теории и скудной практики: «Я видел похожее на лабораторных, меня именно так учили и значит это правильно, критиковать такое нельзя».

Плохое влияние сказывается почти на всех уровнях разработки ПО: на выявлении потребностей, составлении ТЗ, разработке архитектуры, и, конечно, на реализации. Возможно, нет негативного влияния только на выбор стека технологий. Принятие такого подхода формирует у будущих разработчиков мнение, что если код работает, то значит он уже хороший.

Беглый анализ учебных пособий привёл меня к выводу: значительная их часть является откровенной макулатурой, где нет золотой середины — там либо графоманская крайность, которую я привел в пример, либо доведённая до абсурда краткость, где четверть методички — это список использованной литературы, а ещё четверть — пустые разрывы страниц между параграфами.

Некоторые типичные ошибки таких изданий, у которых можно провести аналогию с работой программистов:

Стиль в учебной литературе	Стиль в работе программиста
Изложение материала не опирается на уже имеющиеся знания читателя. Факты описываются каждый раз заново.	Написание велосипедов. Начинающие разработчики часто ещё не умеют пользоваться готовыми решениями или боятся разбираться в том, как они устроены.
Огромные предложения, которые без труда можно разбить на три коротких, лучше проясняющих «поток сознания» автора.	Функция на 500 строк с семью входящими параметрами, из которых второй и шестой передаются по ссылке, а возвращаемое значение является кодом из километрового справочника ошибок.
Безликие имена переменных	Пресловутые a, c, tmp, rez, n, var1, ii, i2
Стремление выносить в оглавление каждое предложение.	Написание комментария к функции/методу, который больше, чем сам код.
Неуместное обобщение контекста прикладной задачи до фундаментальных основ теории (принцип: «от частного к общему»)	Написание функции, работа которой сильно разнится от контекста её вызова и предварительной настройки передаваемых параметров.
Избирательные ссылки на предыдущие и даже будущие утверждения в тексте.	Использование операторов безусловного перехода goto.
Введение «авторских» понятий и терминов, в контексте которых нужно читать весь материал.	Магические числа, глобальные переменные, захардкоженные текстовые константы, ip-адреса и т. п.
Попытка разместить на графиках часть промежуточных вычислений, которые были опущены ранее.	На примере MVC: запросы к базе данных из представления, детали бизнес-логики в контроллерах.
Попытка дополнить ответ чем-то, что подгоняет полученный результат под желаемый.	Написание костылей, которые мне даже стыдно перечислять.
Использование неуместных в контексте данного предмета крылатых выражений, цитат великих античных авторов или отрывков римского права.	Юмористические названия методов, переменных и свойств. Очные совещания со всей командой разработчиков, призванные посвятить каждого разработчика во все детали проекта, в т. ч. находящиеся вне его зоны ответственности.

Математика — это обязательный предмет в любой учебной программе: и школы, и техникума, и вуза. Значит все мы без исключения хотя бы в лёгкой форме уже встречались с некачественной формой подачи. При отсутствии альтернативы это действительно может повлиять на разработчика, который не привыкает думать о чистоте кода. Для него будет вполне естественно писать код, который нужно кропотливо расшифровывать, а не просто читать.

Это неправильный подход, словно когда в пульте от телевизора почти сели батарейки, а человек для решения проблемы начинает сильней нажимать кнопки этого пульта.

Что стоит почитать на тему хорошего написания кода? Лидер моего личного рейтинга — это всё-таки «Чистый код. Создание, анализ и рефакторинг» за авторством Роберта Мартина. Убеждён, что подобная книга обязана быть в библиотеке каждой команды, так как ожидать её наличие в вузе не стоит.

Как бы это можно было бы решить? Для медленно меняющихся (=фундаментальных) знаний — классической механики и основ высшей математики — легко. Для них следует использовать проверенные временем учебники и пособия, отработанные годами, с отточенными до совершенства и вылизанными до чистоты предложениями. К счастью, второй закон Ньютона в наш век не сильно-то поменялся. Фундаментальные знания — это не оперативные Stackoverflow или Q&A, а тем более не каталог парфюмерии, который для сохранения актуальности важно переписывать каждый год с нуля.

Масла в огонь подливает «план публикаций». Именно выполнение плановых показателей порождает тексты посредственного качества. Каждое учебное заведение непременно хочет иметь свой перечень учебной литературы, свою кузницу знаний. Выходит, что в действительности учебная литература ему нужна не лучшая, а только своя. Строгая модерация таких (и вот таких!) публикаций могла бы уменьшить негативный эффект.

P. S. Я уже озвучивал, кому могла бы быть полезна статья. Например, тем несчастным преподавателям, которым в этот момент ставят план на количество опубликованной литературы. Печально, что ситуацию мешает исправлять не только бюрократия. Как я уже писал в начале статьи — я уверен, что кроме программистов проблему плохого написания не понимает никто, поэтому донести мысль до непрограммистов у меня не получится.

P. P. S. Прочитав комментарии (и исправив указанные в статье ошибки), я решил вынести из них несколько замечаний, в т. ч. те, которые не совпали с мнением в статье:

Понимание того, что способ решения и его качество тоже важны, как и результат, приходит только с опытом. Вывод: ноги плохого кода растут ещё и от неопытности и могут в будущем уйти . @hello_my_name_is_dany прав.
Нельзя доводить борьбу с однобуквенными переменными до абсурда - есть много устоявшихся обозначений и в программировании (i, j - счётчики циклов), и в физике (v - скорость, F - сила). Придумывать для них длинные содержательные имена - это придумывание велосипедов, которые уже упомянуты выше. @ivstrelkov выразился более развёрнуто и точно.
@MaximRV навёл на мысль, что статья получилась слишком длинной. Дурной пример заразителен, я был прав!
Непонятная простыня текста в любой нормальной книжке сразу учат писать хорошо. Дурной пример не всегда заразителен.
Хороших книг меньше, чем плохих книг. Хорошего кода меньше, чем плохого. Это неизбежно и, видимо, всё-таки нормально.
Сотрудничество образовательных учреждений с отраслью - куда более лучшее решение проблемы, чем строгий контроль учебных пособий. @karataev_1992 - я к вам присоединюсь в вашей работе.
Несмотря на все недостатки старой математической нотации - она жива. Может быть потому что в ней всё-таки есть много хорошего? Может быть потому что в ней есть не только легаси, но и отточенные веками принципы? @DonVietnam прав.
Формулы и теги почти никто не читает!

Комментарии (53)

hello_my_name_is_dany
25.06.2022 01:53
#24470332
+15
Проблемы схожи, но связи между ними нет, потому что те, кто не изучали высшую математику, математический анализ и тд, делают такие же ошибки в программирование по началу, что и те, кто изучали.

Основные причины такого рода ошибок в том, что задачи математики и задачи программирования похожи - нужно получить результат. И только потом приходит понимание, что как ты решаешь задачу, тоже имеет большое значение.
1. sepetov Автор
  25.06.2022 12:00
  #24471106
  Знаете, ведь вы правы. Понимание приходит потом, когда уже что-то сделаешь. Давайте назовём это опытом? Я это добавлю в статью.

light_and_ray
25.06.2022 02:18
#24470366
+10
Математическая нотация очень удобна для математики. Когда ты на одной волне с преподователем, или с другим человеком, занимающимся математикой, все кристально понятно. Обьяснить словами, или текстом тоже самое на порядок сложнее

Пример на бумажке - это рутинное решение квадратного уравнения, и все оно в целом воспринимается как одно действие. Зачем в нем рассписывать действия и что обозначают переменные?
1. ivstrelkov
  25.06.2022 11:46
  #24471078
  +5
  Присоединюсь к комментарию, но еще добавлю из своего опыта.
  
  Со второго курса уже занимался промышленным программированием параллельно с учебой. В частности, пытался решать уравнения в частных производных или цифровой обработки сигналов.
  
  И я хочу сказать, что даже в программировании математики, на мой взгляд, нейминг одной-двумя буквами более оптимален:
  - Формулы, как правило, очень длинные. Поэтому если выбирать человекопонятные имена переменных (например, speed вместо v), то формула вылезет за пределы экрана и будет тяжела как в поддержке, так и чтении
  - Как правило, никто в математике не оперирует длинными названиями переменных. Поэтому та же самая v будет узнаваться быстрее. А вот speed - медленнее, т.к. мозгу нужно будет в голове смапить speed обратно в v, что отнимает ресурсы. Так что одно-двухбуквенные имена лучше оставлять в таких задачах как минимум ради ubiquituous language
  1. sepetov Автор
    25.06.2022 12:39
    #24471176
    +1
    Тоже присоединюсь. Очень много сущностей имеют устоявшиеся обозначения и формы записей (те же уравнения Максвелла, законы Ньютона и всё-всё-всё). Для них придумывать новые обозначения - однозначное зло. Это ничем не отличается от придумывания своего велосипеда.
  1. gbrdhvndi
    25.06.2022 16:14
    #24471634
    +4
    V это всё же velocity, а не speed.
  1. nin-jin
    27.06.2022 06:19
    #24474920
    +1
    Длинные формулы лучше разбивать на несколько коротких, даже если используете однобуквенные именования.
    
    Но однобуквенные имена за редким исключением осложняют изучение незнакомого кода.

light_and_ray
25.06.2022 02:20
#24470370
+4
Я знаю, что формулы почти никто не читает и даже есть утверждение: каждая формула уменьшает количество читателей вдвое.

Особенно это утверждение применимо к читателям статьи на Хабре ????????‍

MaximRV
25.06.2022 07:23
#24470532
Очень похоже, что те, кто минусанул статью не читали её до конца.
1. sepetov Автор
  25.06.2022 12:03
  #24471114
  +1
  Знаю как минимум одну объективную причину для этого - я всё же явно переборщил с объёмом материала. Видимо, дурной пример методички был и правда заразителен. Пожалуй, я её сокращу, убрав лишнее. Спасибо :-)
  1. MaximRV
    25.06.2022 17:44
    #24471822
    +1
    незнаю за что вас минусанули в этом комментарии, но оставьте статью как есть. я лишь высказал недоумение, когда статься ещё только появилась, что её стали минусовать. Теперь она в плюсе и это не выглядит ненормальным.

iingvaar
25.06.2022 08:58
#24470662
+2
Это общая проблема научного знания.
- Хороших книг меньше, чем плохих книг.
- Хороших статей меньше, чем плохих статей.
- Хорошего кода меньше, чем плохого кода.
- Хороших учителей меньше, чем плохих учителей.
- Тех, кто в результате научился отличать хорошее от плохого меньше, чем тех кто не научился.
Вам удалось сформулировать один из источников проблемы. Предлагаемым вами решением, кстати, пользуется Википедия, где над каждым словом думают десятки компетентных людей. В результате подавляющее большинство статей там являются хорошими. Однако российское образование пришло к той точке, когда атомарные изменения не способны его улучшить. Мои 20-летние наблюдения за средним, специальным и высшим образованием укрепили меня в мысли, что всё целиком нужно сжечь. Я реально надеюсь на это, реформы с нуля возможны.
1. s_f1
  25.06.2022 12:04
  #24471118
  +1
  Вы привели четыре следствия из аксиомы «Хорошего меньше, чем плохого» :)
  По вопросу в заголовке – ноги у плохого кода растут из этой же аксиомы. Плохого кода всегда больше, чем хорошего.
  1. alvltab
    25.06.2022 14:43
    #24471424
    +1
    Нет на свете такой гадости, объяснение которой нельзя редуцировать до «энтропия растёт».
    
    iingvaar
    25.06.2022 23:51
    #24472490
    Есть :) Это эволюция.
1. RouR
  25.06.2022 15:59
  #24471600
  +2
  всё целиком нужно сжечь.
  
  Как бы вы обучали своих детей?
  1. iingvaar
    25.06.2022 23:42
    #24472466
    +2
    Так же как сейчас. К сожалению, всё, что знает мой ребенок, он знает от меня. Но у меня было недостаточно времени и упорства. Абсолютно по всем темам, которых я не касался в наших беседах, он не знает ничего. Школа дала только социализацию, и то весьма сомнительную, гораздо больше дал спорт. Школа сейчас - это как армия, там не нужно, чтобы ребенок что-то узнал, главная ее задача - отвлечение ребенка от нанесения вреда себе. Когда я учился в школе, трава была намного зеленее, просто на порядок. Но я очень далек от мысли, что "советское образование самое лучшее". Самое лучшее должно не стоять на месте, а бежать очень быстро. Первое, что должна будет сделать инициативная группа по реформе образования - это изучить и обобщить существующие мировые практики. Второе - провести люстрацию учителей. Эти люди не должны больше приближаться к детям.

wolfy_str
25.06.2022 09:02
#24470674
+2
На самом деле то что на листочке в начале статьи написано на несколько порядков легче, тех примеров с интегралами. Это всё зависит от понимания, думаю многие со мной согласятся, а двойные, тройные интегралы и далее до сих пор не понимаю как решать.

Вообщем не понятная простыня текста в любой нормальной книжке сразу учат писать хорошо. Только в наших книжках пишут примеры функций с именами типа foo это очень раздражает, тем более не нужны все эти 500 строчек кода, потому что даже функция с на 5 - 10 строчек кода может быть сложной и не понятной и уже её нужно называть правильно. Я не говорю про промышленный код, да я немного столкнулся там функции в 3-4 строчки (три - четыре) которые только возвращают значение немного его изменив, уже требуют внятного названия функций.

И да чем отличается российская литература по программированию и зарубежная? В зарубежной в подавляющем большинстве книг куча воды, да и только запуск программы находится где то на 50-той странице, но! в разы понятнее практически любой книги российских авторов. Ну и учат всегда писать правильно настолько, что даже устаёшь это читать, но с другой стороны мне не хватает сил прочитать наши сложные книги в которых всё описано сложно, а иностранные аваторы пишут слишком водянисто, но понятно в большинстве своём, собственно между этим приходится выбирать.
1. sepetov Автор
  25.06.2022 12:08
  #24471122
  Кстати, а ведь я в статье эту тему не раскрыл (скоро дополню статью). Вы правильно сказали:
  
  простыня текста в любой нормальной книжке сразу учат писать хорошо
  
  Выходит, даже от такой макулатуры может быть положительный эффект. Ну на примере меня, скажем. Я ведь и правда писал бы хуже, если бы не запомнил на всю жизнь тот ужас.

karataev_1992
25.06.2022 12:09
#24471124
+2
Решение проблемы не в строгом контроле выходящих учебных пособий, а в сотрудничестве отрасли с образовательной организацией. Да, вы верно описали проблему нехватки времени на создание качественного продукта. Я преподаватель IT-дисциплин в вузе. Поступаю в аспирантуру, и планирую как раз в диссертационном исследовании данную проблему рассматривать. Однако подтвердить в научном поле мне эту проблему будет крайне сложно, поскольку она в основном предмет холиваров на Хабре и объект мемов в соцсетях, что не может являться репрезентативным источником. Необходима либо всероссийская экспертиза кода выпускников вузов и ссузов, которая скажет, мол, да, выпускники не умеют писать приемлемый код, либо заключения наиболее крупных работодателей, а-ля Сбер, VK, Яндекс. Если у вас подобные данные имеются, или вы желаете какую-то лепту внести в процесс улучшения кода выпускников, буду признателен вашему ответу.
1. sepetov Автор
  25.06.2022 13:02
  #24471218
  Знаете, я не работаю в очень крупной компании типа Яндекса/Контура/VK, поэтому подобных данных у меня нет.
  
  Но некоторую лепту я готов внести - написал в личку.
1. nin-jin
  27.06.2022 06:24
  #24474924
  А какую лепту тут можно внести?
  1. sepetov Автор
    27.06.2022 07:56
    #24474982
    Пожалуй, только кодревью. Но и это сработает только для некоторых студентов. Уж точно не для всех. Я бы даже сказал для единичных.
    
    nin-jin
    27.06.2022 08:50
    #24475082
    +1
    Нужно какое-то более системное решение.
    
    sepetov Автор
    27.06.2022 16:20
    #24477084
    Обеими руками поддерживаю! Но иных возможностей у меня нет, к сожалению, да и работаю я сейчас не в образовании. По-хорошему мне в это вообще нос совать не стоит, раз не моя сфера. :-(

ytm1
25.06.2022 12:14
#24471138
+2
У вас путаница в формулировке задачи про интеграл, там говорится, что нужно найти первообразную от функции y, то есть $\int ydx$ , а в ответе указана лишь сама функция y.
1. sepetov Автор
  25.06.2022 12:15
  #24471142
  Сейчас поправлю, спасибо!

DonVietnam
25.06.2022 12:35
#24471170
+1
Нотации и структура повествования применяемая в математике, уже простите, но применяется много больше времени, чем в принципе существует программирование. Эти две области действительно имеют много схожих вещей, однако когда пишите подобную статью нужно учитывать всю многогранность математики, которая включает в себя множество различных разделов, причем далеко не со всеми есть хоть какая-то родственная связь у программирования. И сдается мне, что за все время существования математики, люди, занимающиеся ей, уже давно выработали удобные им нотации и методологии.

Говоря по своему опыту, человека, который в ВУЗе прочитал несколько книг по математике(да опыт не большой), могу отметить что все вполне себе понятно излагается. А проблемы по типу именования переменных никогда не путают, ещё раз - все эти записи оттачивали многоми годами.

amarao
25.06.2022 13:09
#24471240
Математику и программирование нельзя сравнивать, особенно на операциях с интами, которые всего лишь произведение битов. Во-первых это не числа. Во-вторых, имена, присвоенные этим битам не являются математическими выражениями (чего стоит утверждение x=x+1, из чего можно сделать, что x строго равен бесконечности).

А вот пример программы, похожей на математическую запись:
```
step :: Natural -> Natural
step n
  | even n    = n `div` 2
  | otherwise = 3 * n + 1

collatz :: Natural -> Natural
collatz 0 = 0
collatz 1 = 0
collatz n = 1 + collatz (step n)
```
1. sepetov Автор
  25.06.2022 13:18
  #24471250
  Я же сравнил с исходным кодом учебное пособие, а не математику. Математику я люблю. Проблема плохого стиля конечно же есть в любой дисциплине, о чём я и сказал. Пример с математикой выбрал для удобства, хотя мог бы "нечитаемый шифр" привести из химии.
  1. amarao
    25.06.2022 13:19
    #24471254
    +1
    На самом деле проблема со школьной математикой начинается с того, что один и тот же глиф (=) используется с разными смыслами (определение, соотношение, следствие).
    
    sepetov Автор
    25.06.2022 14:05
    #24471328
    Эта "перегрузка" операторов, кстати, обострилась ещё в Средневековье с распространением печатной литературы. Тогда оттиски были дорогими и их старались экономить. Поэтому разнообразие символов первых печатных текстов всегда было скудным.
    
    Впрочем, в античности тоже было что-то похожее - тогда в дефиците была сама <s>белая</s> бумага, поэтому любые слова часто сокращали. Античность, по-моему, период расцвета аббревиатур и сокращений?
    
    iingvaar
    26.06.2022 07:46
    #24472958
    +1
    Я думал Советский Союз :) СРМТСиБ, СДЮШОР, ВСЕГЕИ.
    
    sepetov Автор
    26.06.2022 11:15
    #24473256
    Точно! Это ещё один пример расцвета "шифротекстовых названий". Кстати, ведь тогда тоже случилась нехватка оттисков - после запрета знака "Ъ" в конце некоторых слов, большевики изъяли его оттиски из типографий. Для случаев, когда он был необходим (объезд, съезд и т. п.) стали использовать апостроф (об'езд, с'езд).
    
    sepetov Автор
    26.06.2022 11:18
    #24473260
    Ах, да, под это ещё и исторический контекст подводили, правда уже позже. Приводили в пример мнение математика Лейбница:
    
    Он считал, что обозначения должны быть максимально краткими. К примеру, Лейбниц говорил: "Зачем использовать две точки для обозначения деления, когда можно использовать лишь одну?".
    
    iingvaar
    26.06.2022 11:33
    #24473280
    +1
    Вот я тоже раньше думал, что это разные смыслы. Мне казалось очень логичным, в частности, что знак логической операции и знак присваивания во многих ЯП разные. Почему бы не перенести это обратно на математику? Однако со временем мне всё меньше так кажется. = это ключевая связка в математике, это её основа. Это то, вокруг чего можно "танцевать", перенося из правой части в левую и из числителя в знаменатель (не всегда). Независимо от того, определение это, отношение, тождество или следствие. Если мы сейчас введем 3 или 4 разных знака, решать системы уравнений станет уже не так легко.
    
    Ndochp
    26.06.2022 12:53
    #24473414
    +1
    Математики это просто фанаты перегрузок символов. Особенно меня впечатлило это в курсе комплексных чисел. "Вот это выражение с синусами и косинусами дает после взятия производной себя же, в вещественных числах таким свойством обладает экспонента, значит и это выражение будем обозначать e^z" и еще много подобного.
    
    iingvaar
    27.06.2022 00:06
    #24474624
    +1
    Наверное, в перегрузках все же есть смысл. Очевидно, что то, что мы называем умножением матриц есть совсем не то, что мы называем умножением чисел. Оно вообще даже не коммутативно. Но оно намного больше похоже на умножение, чем на все остальное, поэтому вряд ли есть смысл изобретать для него новый значок и название. Да и как его со скалярами после этого комбинировать? Все скаляры переводить в матрицы 1х1? Перегрузки операторов открывают невероятную гибкость в математических построениях и легкость в передаче мыслей.
    
    amarao
    26.06.2022 14:08
    #24473626
    Нет, это разные смыслы. Если бы это был один и тот же смысл, то невозможны были бы доказательства от противного, потому что когда мы пришли к утверждению 1=2, то это либо "по определению" (и тогда вселенная развалилась от unsoundness), либо это всего лишь логическое утверждение, содержащее в себе ошибку, что опровергает исходную посылку (допущение).
    
    iingvaar
    27.06.2022 00:13
    #24474642
    +1
    Не любые определения одинаково полезны. Как минимум, они должны составлять непротиворечивую систему. Можно протестировать кучу определений и выбрать самые удобные. Именно так и строится арифметика, например. Поэтому не вижу разницы между "утверждением" и "утверждением по определению". Точно так же не вижу проблем в доказательстве от противного. Вывод противоречит исходным посылкам - значит какая-то из исходных посылок не верна. Или та, которую мы пытаемся доказать. Или та, которую мы 300 лет считали аксиомой.

JuryPol
25.06.2022 14:20
#24471370
+1
Странная статья...

Уважаемый автор, неужели не чувствуете, насколько надуманной является аналогия дурно написанного методического пособия с плохим кодом.

Взять пресловутый листочек. Ощущение создается, что вы просто вывалили набор типовых претензий к плохому коду и сопоставили его с листочком. Да вот беда - не сопоставляется.

"Краткое содержание статьи" - отдельный вопрос. Анонсированы два варианта оформления математического упражнения. Это точно вы взяли для сравнения рекомендуемое странным преподавателем решение конкретного уравнения? Или это некое методическое пособие (с тараканами, справедливости ради) по решению задач по курсу математики вообще? Тщательно подсчитаны количество формул, слов, знаков. А смысл? Фихтенгольц замечательный трехтомник написал, давайте еще и его посчитаем, разница вообще потрясающая получится
1. sepetov Автор
  25.06.2022 14:41
  #24471416
  Нет, абсолютно не надуманная аналогия. Пойдёмте вместе в библиотеку вуза и возьмём новые публикации. Я лично убедился, что это в основном макулатура, написанная для галочки. Аналогия: плохой код тоже пишут для этой самой галочки: "Ну работает же".
  
  А поддерживать такой код потом трудно, но иного выхода нет. Аналогия: читать плохую методичку трудно, но иного выхода нет, если негласно требуют именно её.
  
  Устроившись на работу я лично увидел хороший код и получил возможность сравнить его с плохим. Это оказалось очень полезно. Аналогия: при наличии методичек с тиражом меньше 500 экземпляров у студентов не всегда есть возможность их между собой сравнить - берут то, что осталось.
  1. JuryPol
    25.06.2022 16:21
    #24471646
    Да уж...
    
    Так вот из-за чего делают плохую колбасу... плохие машины... плохие дома... Не тем людям дают писать методические пособия по математике.
    
    Все, вопросов по связи качества кода с учебными пособиями по математике более не имею.
    
    Жаль только, остался непроясненным вопрос о тестировании и и листочке...
    
    MaximRV
    25.06.2022 17:45
    #24471824
    +2
    Ну вот я согласен. Наплевательское отношение ко многим аспектам жизни, оно знаете ли транслируется в другие аспекты.

borovichok13
25.06.2022 16:40
#24471682
Не самый лучший пример решения квадратного уравнения: его можно сократить и он не полон для понимания решения. Следующая строка после нахождения дискриминанта идёт без пояснения, откуда взялись значения.

В жизни ни разу не писал строчку с нахождением дискриминанта. Меня так учили и всегда не понимал за чем эта лишняя строка. Можно сразу писать формулу для нахождения корней. А вот её то в примере - нет! -

Редактор формул в комментариях ещё -тот. Надеюсь, что набранную формулу все поняли. Проще, наверно, было словами описать формулу.

По поводу оператора Goto. Как-то раз на рубеже 90х, чтобы не изобретать велосипед, переписывал программу, опубликованную в книге, на язык без оператора goto. Пришлось помучаться.

Ссылки на предыдущие части в длинном тексте важны. Пример, который вы привели - абсурдный, но при желании можно разобраться. А вот в научной статье, когда даётся ссылка на работу длиной несколько десятков страниц, нужное место в той статье можно искать долго.
1. telpos
  25.06.2022 16:50
  #24471702
  Дискриминант считается, чтобы школьники не впадали в ступор при попытке извлечения корня из отрицательного числа.
1. sepetov Автор
  25.06.2022 16:53
  #24471710
  Да, это очень неприятный пример другой крайности, когда делается отсылка к другому документу или фрагменту. "Найди-ка в нём нужное место" - это словно игры в прятки.

lxsmkv
25.06.2022 17:14
#24471740
+3
Есть цитата Вольфа Шнайдера, ставшая в Германии уже пословицей: "Одному из них придется мучиться. Либо читателю, либо автору." И хотя эти слова изначально подразумевали произведения литературы, это фразу часто цитируют в среде айтишников на докладах по чистому коду и т.п.

Silvestor
25.06.2022 19:09
#24471946
+1
Зачем вы это делаете? Попытка привести к чему то более рациональному в нерациональном приводит к более запутанному чем есть на самом деле.

Есть формула, в ней нет скрытого смысла, она просто формула. Зачем здесь именование? Мы не рассматриваем многостраничное математическое решение, которому может потребоваться доп нотация. Зачем здесь усложнение в именовании?

Не надо по общему судить о частном. Если в больших проектах именование важно, то в математике и примерах в частности нет.

Хватит уже все объединять! Подходите к решению проблем творчески.
1. sepetov Автор
  25.06.2022 19:30
  #24471988
  Да вы чего? Не нужно менять математическую нотацию. Статья о том, что она не подходит для исходного кода, а не для математики.
  
  Зачем здесь именование?
  
  (...)
  
  Если в больших проектах именование важно, то в математике и примерах в частности нет.
  
  В этом и есть посыл статьи - в написании кода именование важно, не нужно тащить в него чуждую нотацию, которая не для него предназначена. Нельзя объединять стиль программирования со стилем методичек посредственного качества.

BobArctor
25.06.2022 20:40
#24472144
Справедливости ради, пример с параграфом 2.3.2.1.1.4 мало отличается от типичной страницы мана за авторством любого из трёх ведущих облачных провайдеров. Только бумажная методичка не умеет в URL, а маны умеют.

Ndochp
26.06.2022 12:47
#24473400
А можно не содержание, а заголовок методички, а то когда я читаю

В первом решении 11 формул, незначительные упущения, есть пояснения и… всего 263 слова. Во втором — три тома, в каждом из которых около 80 страниц формата А5. В среднем на странице умещается 180 слов на русском языке. Итого: около 43 тысяч слов и уже неустановленное число формул.

мне кажется, что меня обманывают, и во втором не поиск первообразной из первого решения.

Red_Nose
27.06.2022 10:00
#24475348
-2
Рецепт: подойди к зеркалу, посмотри. Если там Нарцис - рецепт не действителен :)

Блин, даже свой код через 2-3 месяца (я уже не говорю про год) - какой мудак это писал ?? Чужой - Ад и Нервы.

И "лудший погромизд" - это ТЫ, адназначна ! :))

Единственное, что кроме восхищение ничего не вызывало - Борландовский Turbo Vision (~800кб исходников). Эти ~15 ребят/девчат реально были влюблены в свое дело ! Я на этих ребятах-практиках учился, а не на поцах, которые их сменили, взяв МС-нотацию (пою, что вижу) - библиотека стала 6МБ в Дельфи. А потом борландов "убили" :(

Да, я понимаю, что "2+2 уже все умеют !" - но я не ВЕРЮ, оно ж поломается в произвольном месте. А смотреть 3МБ кода (2кб писателя + остальное - библиотеки) - ну нафиг !

Антипаттерны в написании учебных пособий или откуда растут ноги плохого кода? +20

Пример короткий, пример хороший

Пример длинный, пример плохой

Теперь давайте сравним оба решения

Как это связано с плохим кодом?

Комментарии (53)

sepetov Автор

sepetov Автор

sepetov Автор

sepetov Автор

sepetov Автор

sepetov Автор

sepetov Автор

sepetov Автор

sepetov Автор

sepetov Автор

sepetov Автор

sepetov Автор

sepetov Автор

sepetov Автор

sepetov Автор