Сразу к сути: есть склад, где все бизнес-процессы уже отлажены и в целом всех всё устраивает. Ничего, что даст рост в 30%, сделать уже невозможно, но хочется. Поставлена цель: оптимизировать маршрут, по которому идёт сборщик товаров, чтобы товар собирался быстрее. Результат 2-3% роста вполне устроит. Ограничения:

• останавливать работу склада для экспериментов нельзя

• денег — кроме зарплаты — не выделим

• специалистов в этой области не имеется — свободен только веб-программист, да и тот без профильного образования

• закончить нужно не то, чтобы ещё вчера, но через две недели точно.

Статью можно считать продолжением темы наглядного применения известных алгоритмов где-нибудь в промышленности. В этот раз в работу вступает алгоритм k-ближайших соседей.

Для прочтения знать сам алгоритм k-ближайших соседей не требуется — он очень простой и станет ясен ещё в ходе прочтения. Он чем-то похож на теорему Пифагора, только на стероидах.

Для нетерпеливых сразу обозначу основную идею: скорость сборки товара зависит от того, в каком порядке его собирать. Сборщики собирают товар по бумажным листам примерно такого вида:

Здесь строчки пока что отсортированы по ячейкам: от самой дальней к самой ближней. Ячейки имеют такой формат наименования: /номер_стеллажа/-/номер_полки/-/номер_ячейки/. Стеллажи 01 и 02 находятся у входа и следующие идут по нарастающей. Мы попробуем отсортировать строчки в более оптимальном порядке.

Программирования в статье нет — уклон сделан на последовательность действий, которые приспособят алгоритм к жизни. Любой базовый алгоритм, к сожалению, достаточно сырой, словно осенняя погода за окном, поэтому в первозданном виде в эксплуатацию не пойдёт.

Начнём пристрелку

Если сталкиваемся с поиском оптимального маршрута в первый раз, то с вероятностью 100% поисковик расскажет нам об алгоритме Дейкстры. Беглый осмотр алгоритма покажет, что он не умеет работать с отрицательными весами и имеет ещё несколько минусов. Этой информации ещё недостаточно, чтобы отвергнуть его или, наоборот, продолжить копать под него глубже. Таким образом мы сталкиваемся с первым выбором: ищем новый алгоритм, или дорабатываем этот? В статье про алгоритм Левенштейна мы пошли вторым путём, здесь для примера пойдём первым. Если есть подозрительные особенности алгоритма, важность которых вам не очевидна — это первый звоночек, чтобы вы пошли искать что-то другое. Не стоит считать, что это универсальное правило, но часто это именно так и может экономить время.

Как я уже писал, сборщики работают с помощью сборочных листов. Рабочий день у них идёт так:

1. Печатаем сборочный лист

2. Идём налегке к самой дальней ячейке из листа и от неё направляемся ко всем остальным, постепенно набирая товар в корзинку или тележку

Если бы склад был одноэтажным, а ещё узким и длинным, а ещё без разветвлений, а ещё и без перекрёстков, а ещё с рациональным размещением самих товаров, то текущий принцип работы наверняка можно было бы считать оптимальным. Почему? Потому что самый большой отрезок пути человеку нужно идти налегке, а наибольший груз накапливается уже ближе к зоне выгрузки товара.

Из этого описания уже вырисовываются первые критерии, которые осложняют ручной труд и которые мы учтём в алгоритме. Сейчас мы пока ещё рассмотрим упрощённую версию склада, чтобы не отвлекаться от процесса внедрения алгоритма в жизнь людей.

На каких критериях, влияющих на сборку, остановимся? Для примера попробуем эти:

1. «Этаж» полки на стеллаже, на котором находится эта ячейка

2. Расстояние до ячеек (кстати, как от места старта, так и между ними)

3. Масса переносимого товара

4. Количество «особенных» точек на пути между ячейками

«Особенными» точками считаются повороты и перекрёстки.

А как вообще выбирать эти и другие критерии? Идти на склад, смотреть своими глазами на его работу, а также включать логику. По-хорошему, это всё должен делать бизнес-аналитик, но, как вы помните, у нас его нет.

Первые два критерия сильно связаны с «географией» склада. Остановимся на них подробней. Как их представить в цифровом виде? Ничего нового придумывать не нужно — вы уже сами хорошо знаете эту двухмерную систему координат:

А вот упрощённый пример обозначения стеллажей на такой сетке:

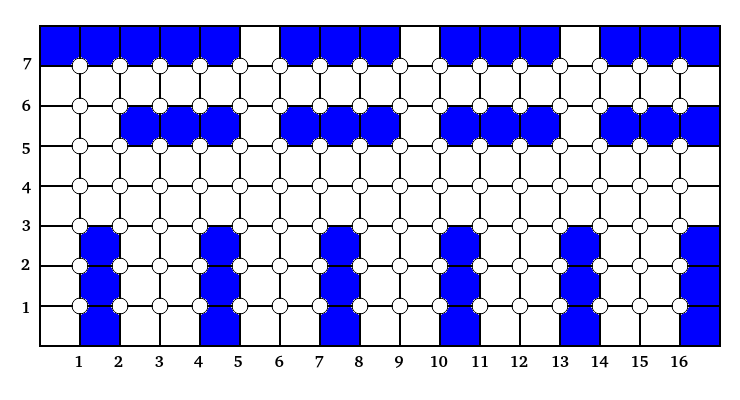
В этом примере все стеллажи кроме одного имеют по три ячейки на полке. Все координаты ячеек отсчитываются от общей точки отсчёта. Для удобства, она размещена в левом нижнем углу, чтобы все значения были положительными числами — это удобней. Этаж учитывается с помощью добавления третьего измерения. Единицы измерения осей пока не нужны.

Для тех кому метрики интересней, чем сам алгоритм — прочитайте текст под спойлером.

Пройдёмся по каждой из них с картинками

Высота полки

С нижних полок собирать товар проще, поэтому их приоритет нужно сделать выше. Полки нумеруются с единицы от нижней к верхней. Первая и вторая полки анатомически одинаково удобны для изъятия товара и поэтому получат одинаковый приоритет. Полки, начиная с третьей, находятся слишком высоко, поэтому для работы с ними нужна стремянка или подъёмник. Подъёмнику особо без разницы куда тянуться — на третью полку, либо на пятую, поэтому все полки от третьей и выше тоже получат одинаковый рейтинг, но не такой, как у двух нижних.

Что это даст сборщику? Это даст возможность сперва собрать товар с одного уровня, а потом полностью с другого. Не нужно будет брать подъёмник для сборки первого товара и затем возвращать, чтобы потом снова взять его для сборки, например, пятого. То, какие ячейки собирать первыми — высокие или низкие — пока оставим открытым вопросом. Это легко можно поменять однократным измерением приоритета.

На уровне БД лучше завести под хранение этажности ячеек отдельную таблицу, так как в реальном складе может потребоваться более тонкая настройка приоритетов. Почему? Во-первых, полки одинакового четвёртого этажа на разных стеллажах могут иметь очень разный приоритет, если какие-то стеллажи недоступны для подъёмников. Во-вторых, приоритет полок со временем меняется, если сезонный товар ставят в проходах между стеллажами, загораживая несезонный товар.

Расстояние до ячеек

Тут объяснять нечего, всё предельно просто:

Все стеллажи расставлены вдоль линий и ни один не стоит под углом. Проходов и дыр в стеллажах нет, поэтому пройти сквозь них невозможно. Из-за этого люди двигаются только по «улицам» и «переулкам». Повороты на общий путь не влияют, даже если сделать их больше, чем нужно:

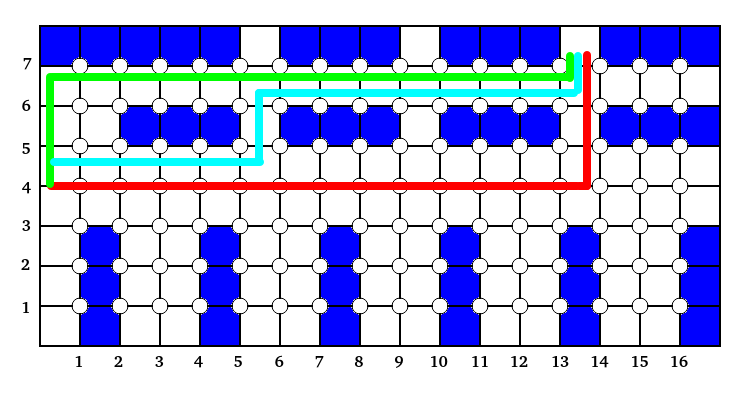
На рисунке обозначено три маршрута: зелёный, бирюзовый и красный. Все три ведут из точки (0;4) в точку (13;7). Визуально заметно, что пройденное расстояние у всех трёх совпало, хотя количество поворотов у всех отличается.

На уровне БД для этого тоже лучше завести отдельную таблицу, так как её часто придётся join-ить с другими. Важно понимать, что единицей измерения расстояния не обязательно будут метры. Также как удава в известном мультике измеряли в попугаях, мы можем измерять расстояние, например, в ячейках или других условных единицах.

Количество особенных точек на пути

Каждый перекрёсток, каждый поворот — это потенциальное препятствие. На перекрёстке, возможно, придётся кого-то пропустить. На нём же абсолютно точно придётся замедлить шаг, так как из-за поворота кто-то может выскочить. На обычном повороте всё аналогично. Возможно, какие-то перекрёстки более сложные, чем другие, а на каких-то поворотах тяжелее развернуться, но опустим и это.

Нам нужно сделать так, чтобы между каждым товаром количество таких точек было минимальным. И тут есть проблема — наличие разных маршрутов. Ещё раз посмотрите на предыдущую картинку:

• у зелёного маршрута есть четыре особенных точки: два поворота и два перекрёстка между ними

• у бирюзового маршрута четыре точки: все из них перекрёстки

• у красного маршрута вообще количество точек можно посчитать по-разному, так как часть стеллажей на него выходят торцом, а часть стоят вдоль. Некоторые промежутки между ними при этом совмещены как в точке (5;4), а вот точка (13;4) — нет.

То есть длина маршрута в метрах у всех такая же, а количество препятствий — нет.

Масса товара

Здесь вообще ничего сложного — информация не требует предварительного исследования и уже есть в WMS. Массу единицы товара умножаем количество и получаем сборочный вес.

Как выглядит алгоритм?

Если человек знает теорему Пифагора, то и с алгоритмом поиска k-ближайших соседей справится. Как я уже намекал, теорема Пифагора является его частным случаем. Сравните теорему:

И наш алгоритм для случая с тремя признаками:

У теоремы Пифагора b — это длина первого катета, а c — длина второго. На рисунке ниже первый катет — это (x₂-x₁), а второй — это (y₂-y₁). Длина катета — это разность координат его конечной точки и начальной, убедитесь в этом из рисунка:

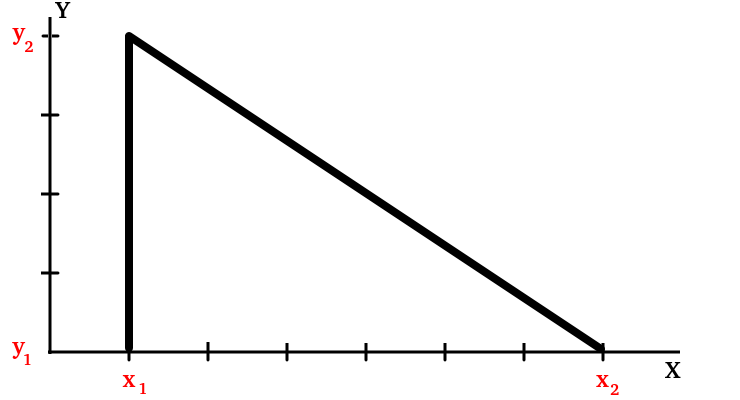
У алгоритма k-ближайших соседей из примера выше есть три параметра: b, c и d. Это тоже разность между значениями этих параметров. Если сравнивать нужно 10 характеристик, то и слагаемых в правой части тоже будет 10.

Вот, собственно, и весь алгоритм. Алгоритмы нередко бывают такими простыми, но часто их преподают странные чудаки на букву «м». Из-за этого не все учащиеся получают даже поверхностную картину. О том, как их применять — ещё меньше. В основном обучение ограничивается зубрёжкой каноничной формулировки и самой обобщённой математической формулы.

На уровне кода наш алгоритм — это функция, которая принимает на вход два товара из сборочного листа, а в ответ возвращает какое-то число. Это число показывает то, как эти товары «близки» между собой. «Близость» — это вовсе не то, о чём вы подумали. Да, речь не об их физической близости: 2 метра, 7 или 10. Близкими они являются по совокупности предложенных мной параметров. Чем меньше число, тем они ближе друг к другу, тем лучше их собирать вместе. Наверное.

Теперь рассмотрим алгоритм ближе к числам. Сравним попарно все товары между собой. Для этого можно заполнить полученными числами вот такую матрицу:

Покажу пример того, как нужно начинать расчёт и исправлять в нём первые ошибки/проблемы. Давайте вспомним метрики:

1. «Этаж» полки на стеллаже

2. Расстояние до ячейки

3. Масса товара

4. Количество «особенных» точек на пути

Сравним обычные блины (товар №1) из нашего сборочного листа с блинами со сгущёнкой (товар №2). У них третья и вторая полка (этаж) соответственно. Масса у первых, например, 40 г, а у вторых 80 г. Расстояние мы измеряем линейкой и получаем, допустим, 20 метров до первых и 28 метров до вторых. Количество особенных точек считаем на пальчиках и насчитываем 3 и 4. Черновой вид формулы у нас получается такой:

Думаю, теперь по алгоритму вопросов больше не осталось и как действовать программисту — ясно. Но внимательные и критически настроенные читатели сразу увидят в алгоритме недостаток: критерии неравноценны. Например, масса блинчиков вносит куда более существенный вклад, чем высота полки. А ещё в текущем виде формула зависит от единиц измерения. Если мы начнём измерять массу в килограммах, то результат кардинально изменится:

Это противоестественно, ведь ситуация с товаром не поменялась, а результат уже другой!

Решение для этих проблем уже придумали, причём оно одно для обеих: нормализация. Её идея заключается в том, что в формулу нужно подставлять не сами величины, а их преобразованные версии. Как их преобразовывать? Придумано несколько вариантов, я покажу один из них:

После такого преобразования все критерии будут лежать в интервале от 0 до 1 и без всяких единиц измерения. Это очевидный момент, или всё же не очень?

С алгоритмом разобрались, а как это воплощать в жизнь?

Нужно «всего лишь» это:

1. Какая-нибудь база данных, в которой хранятся все метрики, перечисленные выше.

2. Какой-нибудь показатель, который позволит сказать, что наш алгоритм хуже или лучше прежнего

Как вы понимаете, из первого у нас нет почти ничего. Об этом можно написать целую диссертацию, но многочисленные подробности я опущу. Это самая «опущенная» часть статьи — к изучаемому алгоритму она отношения имеет очень мало. С другой же стороны, управленческий процесс — не менее интересная составляющая часть рабочих будней. Кому этот момент интересен — для вас следующий спойлер.

А по второму пункту? Аналитики и здесь могут развернуть целое совещание, придумав самые разные показатели от простых до сложных. На мой взгляд, всё гораздо проще — это время. Помните первоначальную формулировку вопроса? Товар должны собирать быстрее.

Странно, но это всё

По итогу у нас есть понимание и как работает алгоритм k-ближайших соседей, и проблемы, которую он должен решить. Также мы знаем, как найти и оцифровать требуемые характеристики ячеек, а алгоритму нужны их нормализованные значения.

В конечном счёте, вся работа программиста теперь заключается в реализации обычных арифметических действий с выборкой чисел из БД. В моём случае применение алгоритма принесло весьма скромное увеличение скорости сборки, но затем он перекочевал во внезапно появившуюся волновую сборку, где оказался гораздо полезней. Со второй попытки для этих же целей я стал смотреть в сторону генетических алгоритмов. На эту тему я когда-нибудь сделаю отдельную статью.

P. S. Я бы сам с удовольствием почитал другие примеры применения алгоритмов. Любопытно посмотреть, как бездонный кувшин народной смекалки орошает наши бескрайние поля трудовых будней.