Расчет значения синуса простой математикой / forpes.ru

Главная
Расчет значения синуса простой математикой

Расчет значения синуса простой математикой +8

03.08.2022 13:02

Hid-K 25 6700 Источник

Предисловие

Навязчивая идея посчитать синус угла, используя простые мат. операции появилась еще давно, и я, тихим вечером копаясь в Desmos'е, обнаружил сходство графика обычной функции-треугольника, возведенной в некоторую степень, с полу периодом синуса, тогда-то ко мне и пришло просветление!

Начало

Для начала была создана та самая функция с периодом в $\pi$ , которая должна в дальнейшем станет нашей синусоидой:

$\left|\frac{\operatorname{mod}\left(x,\ \pi\right)}{\frac{\pi}{2}}-1\right|$

Результат деления с остатком имеет диапозон $[0;\pi]$ , что не соответствует диапазону значений синуса , так что делим результат на $\frac{pi}{2}$ , что дает нам необходимый диапазон , который в дальнейшем позволит нам получить необходимую форму графика.

После приведения диапазона к необходимому виду - превращаем функцию к необходимой форме треугольника. Для этого необходимо вычесть из нее единицу и взять модуль от получившегося числа.

Сходство

На выше приведенном изображении можно увидеть 2 графика:
Зеленый - синус
Красный - наша функция ( функция инвертирована ), возведенная в степень 1.7, подобранную методом тыка.

После сопоставления графиков отлично видно их сходство. Из-за сходства сложно разглядеть график синуса, так сильно они сходятся с подобранной степенью.

Знак периода

Нашей функции не хватает знака периода. его очень просто получить, используя то же самое деление с остатком:

$\operatorname{mod}\left(x,2\pi\right)$

Ее период не совпадает с необходимым, так что инвертируем ее:

$\pi-\operatorname{mod}\left(x,2\pi\right)$

И получим ее знак, используя функцию калькулятора:

$\operatorname{sign}\left(\pi-\operatorname{mod}\left(x,2\pi\right)\right)$

Получаем следующий график:

Теперь умножим нашу функцию-"недосинус" на функцию знака:

$\operatorname{sign}\left(\pi-\operatorname{mod}\left(x,2\pi\right)\right)\left(1-\left(\left|\frac{\operatorname{mod}\left(x,\ \pi\right)}{\frac{\pi}{2}}-1\right|\right)^{1.7}\right)$

Получаем следующий график:

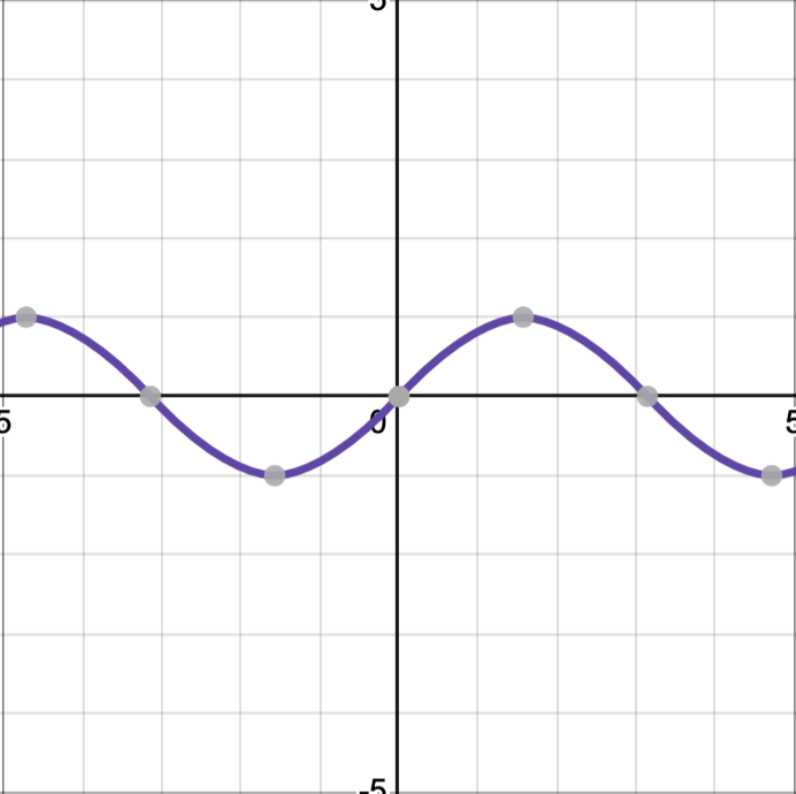
Уже очень похоже, но не то. Нужно избавиться от магической константы 1.7.

Магическая константа

Особо заморачиваться на станем. Просто выдернем необходимый кусок функции и найдем необходимую степень через логарифм:

$\log_{\left|\frac{\operatorname{mod}\left(\frac{\pi}{4},\ \pi\right)}{\frac{\pi}{2}}-1\right|}\left(1-\left|\sin\left(\frac{\pi}{4}\right)\right|\right)$

Таким образом считаем значение магической константы. Дадим имя константе, например $\mu$ .

Таким образом наша функция стала выглядеть следующим образом:

$\operatorname{sign}\left(\pi-\operatorname{mod}\left(x,2\pi\right)\right)\left(1-\left(\left|\frac{\operatorname{mod}\left(x,\ \pi\right)}{\frac{\pi}{2}}-1\right|\right)^{\mu}\right)$

И отличие от графика "калькуляторного" синуса стало совсем незаметно на графике.

Погрешность

Данная формула имеет незначительную погрешность относительно "калькуляторной". Стоит ее посчитать.

Для подсчета возьмем угол 45 градусов, поскольку именно при таком значении наблюдается наибольшая погрешность.

Для измерения погрешности просто посчитаем расстояние от точек на окружностях, нарисованный с помощью "калькуляторного" синуса и нашей формулы.

$d_{cos}=\cos\left(a\right)-c_{os}\left(a\right)$ $d_{sin}=\sin\left(a\right)-s_{in}\left(a\right)$ $d_{trig}=\sqrt{\left(d_{cos}\right)^{2}+\left(d_{sin}\right)^{2}}$

Получаем следующее значение: $5.5511151231×10^{−16}$

Погрешность крайне мала, потому, считаю, ей можно пренебречь.

Заключение

Создание данной функции не было подкреплено каким-либо поводом. Она была создана исключительно в целях саморазвития и утешения внутренней навязчивой идеи.

Благодарю за прочтение статьи. *занавес*

Комментарии (25)

Keeper13
03.08.2022 13:10
#24593608
+14
Даст ли это какой-то выигрыш в скорости вычисления по сравнению с рядом Тейлора, например?
1. Refridgerator
  04.08.2022 06:23
  #24595664
  Нет.

iig
03.08.2022 13:16
#24593626
+16
Возведение в степень - не очень простая математика.

mobi
03.08.2022 13:21
#24593638
+7
В точке pi/4 значения будут совпадать в точности, поэтому возьмите лучше pi/8. А еще лучше постройте и приведите в статье график ошибки от аргумента.

UrsusPuh
03.08.2022 13:45
#24593738
+2
А у меня есть арктангес через аппроксимацию полиномом второй степени. Аппроксимируется собсно четверть окружности, потом всё сводится к ней. Надо было для обработки сквт. Собсно по четвертям окружности:
1. t = arctan(sin/cos)
2. t = PI/2-arctan(cos/sin)
3. t = PI/2+arctan(-cos/sin)
4. t = PI-arctan(sin/-cos)
5. t = -PI+arctan(-sin/-cos)
6. t = -PI/2-arctan(-cos/-sin)
7. t = -PI/2+arctan(cos/-sin)
8. t = -arctan(-sin/cos)
ф-я аппроксимации: y= -0.0915 x^2 + 0.3434x - 0.0015

если x < 0.1 то y = x;

Работает быстро, считать можно даже без плавающей точки.
1. sepetov
  03.08.2022 13:52
  #24593758
  +17
  Просто оставлю это здесь. Вдруг кто не знает.
  
  Приближённая формула для вычисления десятичного логарифма числа X без калькулятора и даже без особых умственных усилий:
  
  Целая часть - количество цифр в числе X минус один.
  
  Дробная часть - первая цифра числа X плюс два.
  
  Уточняющее исключение: дробная часть равна первой цифре исходного числа, если она единица или девятка
  
  Примеры:
  
  lg(456) = 2,6
  
  lg(4567) = 3,6
  
  lg(1234) = 3,1
  
  lg(12345) = 4,1
  1. Rsa97
    03.08.2022 15:59
    #24594218
    +3
    Стоит учесть, что это правило для целых чисел. Для дробных необходимо ещё одно правило
    lg(x / 10ⁿ) = lg(x) − n
    lg(0.456) = lg(456 / 1000) = lg(456) − 3 = −0.4
  1. RumataEstora
    04.08.2022 08:03
    #24595786
    Правила 2 и 3 сомнительны
    
    lg(19) = 1.3
    
    lg(42) = 1.6
    
    lg(45) = 1.7
    
    sepetov
    04.08.2022 13:12
    #24596636
    В первом примере, конечно, есть погрешность в десятых долях ответа. Считая "на глаз" lg(19) якобы должен быть равен 1.1, хотя 1.28 - точнее. Ну, куда деваться? Для кустарных прикидок сойдёт.
    
    Во втором таких расхождений нет. Для lg(42): количество цифр - 2, значит целая часть ответа (2-1)=1. Дробная часть ответа равна 6, так как первая цифра в числе 42 - это цифра 4, а правило предлагает его увеличить на 2.
    
    В третьем примере ответ около 1.65, так что с точностью до десятых результат хороший :-) Жить можно :-)

azudem
03.08.2022 13:48
#24593746
+12
Осталось за малым -- научится вычислять возведение в степень 1.7.

Rsa97
03.08.2022 14:34
#24593964
+24
sin(x°) = 4x(180 − x)/(40500 − x(180 − x)), x ∈ [0, 180°]
Бхаскар I, 629 г. н.э.

isden
03.08.2022 14:52
#24593996
+2
А может проще и точнее хранить табличные значения для 1/4 волны (если ресурсы позволяют конечно)?
1. Keeper13
  03.08.2022 15:14
  #24594068
  +2
  В первом Doom-е так и сделали, насколько я помню.

fk0
03.08.2022 20:18
#24594928
+2
Все калькуляторы считают синусы кордиком (CORDIC). Для чего нужны лишь сдвиги, сложения и простейшие битовые операции. Приведённые же выше способы совсем не тривиальны, так как требуют операций умножения, деления и сложения над числами с плавающей точкой (или большими целочисленными).

Конечно, если есть FPU то разложение в ряд Тейлора -- быстрей. Но на условном 8-битном контроллере быстрей CORDIC.
1. akhkmed
  04.08.2022 00:19
  #24595392
  Кстати да. CORDIC использовался и в 8087, и в целочисленных системах: например в этой старой статье есть реализация для 16-разрядных типов данных, хотя она может быть адаптирована для любой точности. Он действительно использует только сложение, вычитание и сдвиги и является быстро и гарантированно сходящимся. Возведение в нецелую степень выглядит не такой простой математикой.
1. r9wep
  04.08.2022 10:13
  #24596070
  +1
  псс, cordic на верилоге (переложен прикола ради с Си) не желаете? ))

me21
03.08.2022 22:47
#24595218
Но зачем?

maisvendoo
04.08.2022 02:33
#24595556
Теперь поместите вашу существенно нелинейную (с разрывами второго рода) функцию в правую часть дифуры, и наслаждайтесь, пытаясь интегрировать это численно

Refridgerator
04.08.2022 06:22
#24595662
+2
По сути, вы пытаетесь аппроксимировать функцию cos(x·pi/2) функцией 1-x^k на интервале [0,1]. Проблема в том, что в вычислительном плане в этом нет никакого смысла — вычисление возведения в дробную степень делается через логарифм и экспоненту, а они (особенно логарифм) намного более трудозатратны по сравнению с вычислением непосредственно синуса.

Refridgerator
04.08.2022 06:41
#24595682
+3
Навязчивая идея посчитать синус угла, используя простые мат. операции
Держите вариант с тремя знаками после запятой в диапазоне [-pi/2,pi/2]:
1. auddu_k
  04.08.2022 09:58
  #24596016
  +1
  Так в статье интересен не сам результат, а способ вывода и способ как до этого вывода дошли :-)
  
  Как вот вы получили такой удивительно простой результат?
  1. Refridgerator
    04.08.2022 10:21
    #24596096
    +2
    1. Выбрал для аппроксимации функцию (a·x+b·x³)/(1+c·x²);
    2. Составил систему из двух уравнений, определяющих значение (1) функции и производной (0) при x=pi/2;
    3. решение дало значения коэффициентов a и b выраженных через c;
    4. коэффициент c подобрал экспериментально по графику, визуально минимизируя максимальное отклонение и аппроксимировал его рациональным числом;
    5. подставил все значения в исходную функцию и упростил.
    
    Всё это конечно не вручную, а в Mathematica.
    
    auddu_k
    06.08.2022 06:58
    #24602434
    Круто!
    А откуда пришло начальное уравнение?
  1. Refridgerator
    04.08.2022 11:12
    #24596212
    +3
    Если вас привлекает простота, то лучше так:
    
    И точнее получается, 4 знака после запятой.

Sergey_zx
04.08.2022 13:23
#24596676
+1
Кому по душе арбуз, а кому свиной хрящик.

Хочется точно, следуем учению брата Тейлора. Хочется быстро, делаем таблично.