В первой части кратко описан механизм шифрования\дешифрования и проведен предварительный криптоанализ машины. Основным отличием SIGABA от предыдущих роторных машин шифрования стала система рандомизации движения роторов. Уильям Фридман понял, что для повышения безопасности роторных машин нужно уменьшить регулярность движения ротора. Ему пришла в голову идея ввести хаотичность в движение ротора с помощью перфоленты. Рисунок отверстий считывался набором электрических щупов, которые замыкали цепь только тогда, когда под ним проходило отверстие. В результате использования ключевых лент регулярное, предсказуемое движение одометра предыдущих машин было устранено.

Движение роторов зависело от случайно расположенных отверстий на бумажной ленте. Если бы у принимающей станции была такая же ключевая лента, она могла бы декодировать переданное сообщение.

В предыдущей статье отмечена подверженность SIGABA атакам по принципу «разделяй и властвуй» и кратко описаны два этапа новой атаки такого типа:

1. Создание ранжированного списка наиболее вероятных настроек ротора шифрования и пошаговых последовательностей.

2. Обработка возможных настроек роторов шифрования и пошаговых последовательностей, созданных (и ранжированных) на первом этапе.

Продолжим.

Первый этап

Сначала опишем упрощенный и «дорогостоящий» алгоритм реализации первого этапа, чтобы проиллюстрировать основные принципы, оптимизированный алгоритм, процесс ранжирования и подготовки вариантов настроек роторов шифрования для второго этапа.

Общая идея была представлена выше. Отдельно тестируем каждую возможную конфигурацию роторов шифрования. Пять роторов шифрования выбираются из набора (10 роторов, как вы помните роторы шифрования и управления взаимозаменяемы), которые можно установить как в прямом, так и в реверсивном направлении. 

Для каждой конфигурации проверим все возможные начальные положения роторов шифрования — всего 26⁵ = 11881376 = 2^23.5. Итак, общее количество тестируемых комбинаций (конфигурация и начальные положения пяти роторов) — 2^19.9+23.5 = 2^43.4.

Для каждой начальной позиции, например, AAAAA или HJYUI, сначала проверяем, правильно ли роторы шифров расшифровывают первый символ зашифрованного текста, т. е. соответствует ли расшифрованный символ первому известному символу открытого текста. Если эта проверка прошла успешно, проверяем, существуют ли позиции, которые могут быть достигнуты из этой начальной позиции путем применения действительного пошагового шаблона, так чтобы второй символ зашифрованного текста также был правильно расшифрован.

Теоретически существуют возможные 5-битные шаблоны для пяти роторов шифрования, которые будут выполняться после каждого шифрования или дешифрования символа. Однако, как обсуждалось ранее, для модели CSP-889 допустимы только 30 из этих шаблонов, а для CSP-2900 — только 31.

Если ни один из шаблонов шага не приводит к новой позиции, в которой второй символ зашифрованного текста правильно расшифрован, мы отбрасываем начальную позицию. В противном случае мы рекурсивно повторяем процесс для третьего символа, четвертого и так далее, пока не обработаем все известные символы открытого текста.

Из предыдущих исследований известно, что, хотя после проверки каждого символа выживает только одна из 26 начальных позиций, количество путей, то есть последовательность позиций и промежуточных шаблонов, так что роторы шифрования правильно дешифруют зашифрованный текст, увеличивается экспоненциально, в 30/26 = 1.154 раза на каждый проверенный символ. Аналогично, это число увеличивается в 31/26 = 1.192 раза для модели CSP-2900. Результатом этого упрощенного алгоритма первого этапа является набор настроек шифратора и пошаговых последовательностей/путей.

При проверке всех возможных начальных позиций в последовательности символов зашифрованного текста одна и та же позиция ротора шифра может быть достигнута несколько раз разными (объединенными) путями. Следовательно, простое повторение упрощенного алгоритма со всех 11881376 начальных позиций по всей последовательности символов зашифрованного текста явно расточительно и неэффективно.

Для оптимизации алгоритма нужно создать полный граф всех объединенных путей для заданной конфигурации шифратора, используя эффективный метод обхода графа — поиск в ширину (BFS). Сначала мы генерируем граф с n слоями узлов, где n — длина известного открытого текста. Каждый уровень i  включает в себя узел для каждой позиции роторов шифрования, в которой i-й символ зашифрованного текста может быть расшифрован для получения i-го символа известного открытого текста, где (1 ≤ i ≤ n). Поскольку случайные позиции имеют вероятность 1/26 правильной дешифровки данного символа зашифрованного текста, ожидается, что каждый слой примерно содержит 11881376/26 = 456976 узлов.

Ребра графа соединяют пары узлов, принадлежащих соседним слоям, скажем, один на уровне i, а другой на уровне (i + 1). Соединяем узлы ребром тогда и только тогда, когда узел на уровне (i + 1) представляет позицию ротора шифрования, которая может быть достигнута из позиции, представленной узлом на предыдущем уровне, с допустимым шаблоном шага, и в обеих позициях соответствующий символ зашифрованного текста может быть расшифрован, чтобы соответствовать соответствующему символу открытого текста.

Начинаем строить граф с заполнения узлов каждого слоя. Затем генерируем ребра, слой за слоем, с прямым обходом BFS, начиная с первого слоя, проверяя все допустимые пошаговые шаблоны в каждой позиции каждого слоя. Сложность такого процесса линейна, порядка n × 456976 × 30 для CSP-889 (или n × 456976 × 31 для CSP-2900).

Упрощенный пример показан на рисунке 9. Для наглядности показаны только три уровня, и на каждом уровне i  только подмножество позиций роторов шифрования, которые правильно дешифруют i-й символ зашифрованного текста. Каждое ребро указывает шаблон шага, то есть роторы, которые шагают между соединенными узлами. Видно, что в узел BBBBB в третьем слое входит более чем в один путь (объединенные пути). Некоторые узлы, такие как AABBB на первом уровне, тупиковые. Другие, такие как BABBB на втором уровне, не могут быть достигнуты ни из одного узла предыдущего уровня.

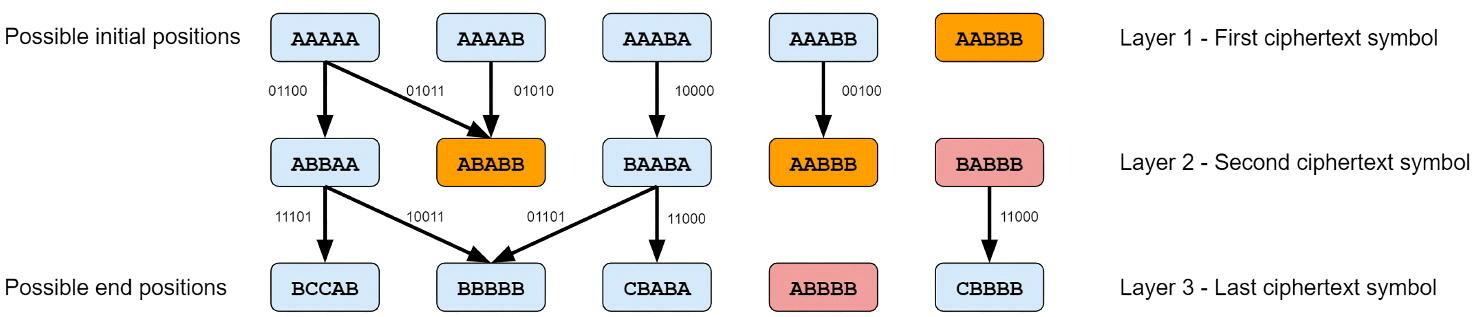
Нас интересуют только те пути, которые начинаются с допустимой начальной позиции на первом уровне и заканчиваются в допустимой позиции на уровне n. Следовательно:

— нужно отбросить неподходящие узлы первого уровня. Это достигается путем удаления любого узла на уровне (i + 1), который остается без входящего ребра после обработки всех узлов уровня i во время прямого обхода BFS;

— также необходимо удалить любой узел, из которого невозможно достичь допустимой позиции на уровне n. Это достигается с помощью дополнительного обратного обхода BFS, в котором мы сначала удаляем узлы из слоя (n — 1), не имеющие исходящих ребер в узлы слоя n. Затем повторяем процесс для слоя (n – 2), слоя (n – 3) и так далее, пока не достигнем второго слоя.

В результате сохранятся только узлы, через которые можно проложить путь от допустимой начальной позиции до уровня n.

Возвращаясь к упрощенному примеру на рисунке 9, после удаления ненужных узлов и ребер мы получаем уменьшенный граф, показанный на рисунке 10. 

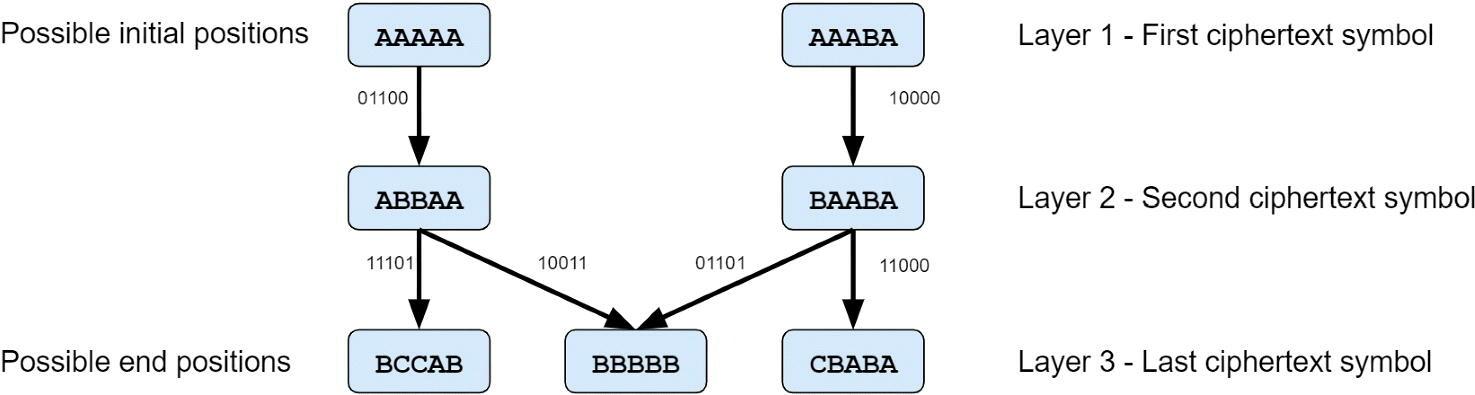
В результате получим четыре релевантных пути:

1. AAAAA → (01100) → ABBAA → (11101) → BCCAB

2. AAAAA → (01100) → ABBAA → (10011) → BBBBB

3. AAABA → (10000) → BAABA → (01101) → BBBBB

4. AAABA → (10000) → BAABA → (11000) → CBABA

Проведем моделирование с n = 100, чтобы получить количество релевантных узлов в различных слоях после прямого и обратного обхода. Первый и последний уровень имеют наибольшее количество позиций. В одном из внутренних уровней графа количество узлов является наименьшим, около 1/7 от количества узлов в первом или последнем слое.

Скоринг путей

Граф, построенный с помощью оптимизированного алгоритма, по-прежнему содержит тысячи узлов на каждом уровне и является достаточно сложным и разветвленным. Основная задача модернизации атаки заключается в определении наиболее вероятных сквозных путей, их ранжирования и выбраковки менее правдоподобных из них. Для этого каждый путь получит свою оценку. Существует два общих подхода к оценке пути:

— Индивидуальная оценка каждого пути в графе. Этот подход требует обширных вычислений, так как количество путей экспоненциально увеличивается с n.

— Совместная оценка объединенных путей, начинающихся в одном и том же узле и заканчивающихся в одном и том же узле, с помощью единого вычисления, основанного на совокупном количестве промежуточных шагов каждого ротора.

Первый подход более точен, с другой стороны, второй подход проще в реализации и гораздо менее затратен, и именно он используется в данном алгоритме. Далее покажем, что он достаточно точен для достижения высокой вероятности успеха.

В процессе эксперимента произведем оценку нескольких методов скоринга объединенных путей с одинаковыми начальными и конечными позициями. Смоделировано большое количество подлинных объединенных путей с n = 100 и случайно сгенерированных путей для сравнения. Цель состояла в том, чтобы найти метод оценки с оптимальным балансом между минимизацией ложноотрицательных результатов (FN, false  negatives), т.е. исключения подлинных путей, и ложноположительных результатов (FP, false  positives), т.е. принятием неподходящего пути.

Стоимость FN — снижение общего шанса успеха всей атаки. Стоимость FP заключается в увеличении времени обработки на втором этапе для обработки неправильных путей, что также может привести к снижению вероятности успеха в случае, когда вычислительные ресурсы ограничены, и не все результаты первого этапа могут быть обработаны на втором этапе.

После продолжительной эмпирической оценки нескольких методов скоринга объединенных путей, в конечном итоге была выбрана следующая функция оценки:

где рr — количество шагов ротора шифрования r по пути, деленное на количество ребер на пути (n — 1), а n количество узлов пути.

Следует отметить, что за исключением нереальных сценариев, оценка двух путей, которые начинаются в одной и той же позиции и заканчиваются в одной и той же позиции, одинакова. На основании 10 млн. симуляций для модели CSP-889 с n = 100 установка (минимального) предела оценки, равного −1.63, не приводит к FN. Тем не менее, приводит к соотношению FP 0.004. Точно так же пороговое значение −1.50 не приводит к каким-либо FP, но приводит к FN с отношением 0.036.

Дело осложняется еще и тем, что на баланс FN/FP существенное влияние оказывают конкретные настройки индексного ротора, а точнее, категория, к которой эти настройки относятся (см. рис.7 в первой части). Например, средний балл для пути с настройками индексного ротора в категории 1 составляет −1.23. Моделирование настроек индексного ротора в категории 1 показывает, что пороговое значение −1.50 не приведет ни к FN, ни к FP, так что правильный путь может быть легко идентифицирован. С другой стороны, средний балл для пути с настройками индексного ротора в категории 88 составляет −1.49.

Моделирование показывает, что хотя пороговое значение −1.50  по-прежнему не приведет к отсутствию FP (для 10 млн. симуляций), оно приведет к гораздо более высокому коэффициенту FN, около 0.23 (то есть правильный путь, вероятно, будет пропущен в 23% случаев).

Удивительно, но ситуация для модели CSP-2900 кардинально отличается и гораздо более благоприятна для атаки. Средний балл с настройками индексного ротора, относящимися к категории 1, наиболее благоприятной категории, составляет −1.06, а для тех, которые относятся к категории 80, наименее благоприятной, он составляет −1.17. С другой стороны, на случайных путях роторы с большей вероятностью будут делать шаг, чем сохранять свое положение. Можно выбрать оптимальный порог для CSP-2900, равный −1.42. Оптимальный предел — это тот, который однозначно отличает случайный путь от подлинного, так что нет ни FP, ни FN для каждой из 80 категорий настроек ротора индекса. На практике это означает, что при n = 100 после первого этапа остается только один путь, а на втором этапе нужно будет проверить только этот единственный путь. Если мы готовы принять небольшое соотношение FN, также возможно эффективно оценивать пути модели CSP-2900 только с n = 60 (известные символы открытого текста). Пороговое значение −1.33 приводит к отсутствию FP (для 10 млн. симуляций) и коэффициенту FN всего 0,001.

Отбор и подготовка путей ко второму этапу

Подготовка входных данных для второго этапа включает извлечение путей, выбраковку путей с низкой оценкой, объединение путей с общими важными маршрутами в подграфы и ранжирование этих подграфов.

Количество путей увеличивается экспоненциально по мере обработки каждого нового уровня графа. Теоретически можно просто построить все сквозные пути, представленные графом, оценить их и ранжировать, но это неэффективно. Хотя метод оценки наиболее точен для полных путей с n = 100, он также может быть рассчитан для частичных путей с меньшим количеством уровней.

Для этой цели используются менее строгие пределы, чем предел для классификации полного пути. Если оценка частичного пути, ниже порогового значения, можно сразу отбросить этот частичный путь. На рисунке 11 показаны пределы, используемые для фильтрации частичных путей различной длины. Эти разрешающие пределы гарантируют, что вероятность пропуска частичного подлинного пути будет чрезвычайно низкой (менее 0,0000001). Фильтрация частичных путей, которые не проходят эти пороговые значения, не только значительно снижает экспоненциальный рост, но также уменьшает итоговое количество путей после каждого уровня.

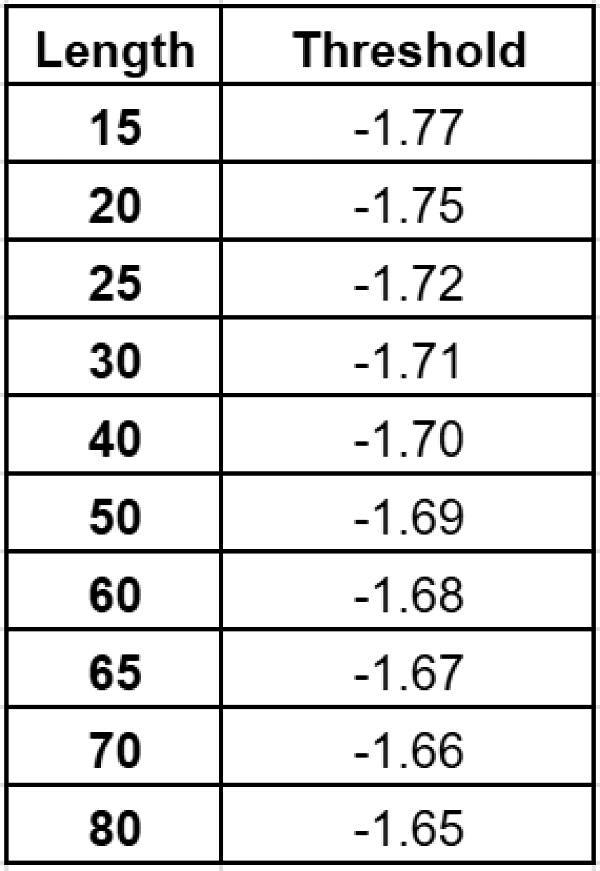
Окончательный предел для выбора сквозных путей (со 100 узлами устанавливается в начале атаки, обычно примерно −1.50 (для CSP-889). Этот предел используется для оценки сквозных путей, отфильтровывая маловероятные, еще больше уменьшая количество тех сквозных путей, которые необходимо протестировать на втором этапе, до не более нескольких тысяч в худшем случае, и в большинстве случаев значительно меньше.

Теоретически на втором этапе можно было бы по отдельности обработать все оставшиеся сквозные пути. Однако для дальнейшей оптимизации атаки нужно не только отфильтровать маловероятные пути, как описано выше, но и объединить несколько путей вместе для более быстрой проверки. Эта дополнительная проверка и объединение выполняются на графе, представляющем допустимые позиции и пошаговые последовательности для заданных настроек шифратора, следующим образом:

— сортируем оставшиеся сквозные пути в графе в соответствии с их оценками;

— оставляем только 1000 лучших путей и отбрасываем остальные;

— удаляем маршруты, оценка которых ниже, чем у пути с самым высоким рейтингом минус 0.2;

— обрабатываем оставшиеся пути от самого высокого ранга к самому низкому и пошагово строим новый граф, объединяя в него узлы и ребра обрабатываемых путей;

— если количество добавленных к новому графу узлов превышает 5000, мы отбрасываем все оставшиеся необработанные пути;

— если текущий граф включает более 100 непересекающихся подграфов, мы отбрасываем все оставшиеся пути, которые еще не были обработаны; 

— результатом этого процесса является граф с одним или несколькими непересекающимися подграфами, каждый из которых представляет один сквозной путь (несколько взаимосвязанных) или несколько объединенных сквозных путей;

— каждому непересекающемуся подграфу присваивается оценка, которая представляет собой оценку наилучшего сквозного пути, который он содержит;

— непересекающиеся подграфы сортируются и предлагаются в качестве входных данных для второго этапа.

Сложность топологии графов, созданных на первом этапе, оказывает большое влияние на то, как эти графы могут быть эффективно обработаны на втором этапе. Иллюстрации графов с различными уровнями сложности приведены в конце статьи. Тот факт, что мы имеем дело с подграфами, а не с однозначными сквозными путями, создает несколько проблем, решаемых на втором этапе.

Второй этап

Сначала также как и в первом этапе опишем упрощенный и менее эффективный алгоритм реализации этапа для иллюстрации основных принципов. Потом оптимизируем его. Основной целью второго этапа является проверка допустимости отобранных путей для реконструкции последовательности работы шифратора с допустимыми настройками управления и индекса.

Упрощенный алгоритм реализации второго этапа атаки

Один из способов проверки возможных настроек роторов шифрования состоит в том, чтобы извлечь все начальные позиции из первого уровня в подграфе, игнорируя пути и все последующие уровни, и протестировать их одну за другой. При таком подходе тестирование каждого варианта превращается в достаточно трудоемкую задачу.

Хотя оптимизация и фильтрация на первом этапе значительно сократили количество вариантов, проверка оставшихся вариантов все равно требует значительных вычислительных мощностей, поэтому проведем ряд оптимизаций:

1. Тестирование сквозных путей и обход индексных роторов.

Можно уменьшить сложность второго этапа, оценив сквозные пути вместо начальных позиций роторов шифратора (в сочетании с выбором, порядком и конфигурацией направления ротора шифратора). Ранее описано, как упрощенный алгоритм проверяет варианты настроек роторов шифратора, выполняя расшифровку для каждого варианта. Упрощенный алгоритм использует только начальные позиции и игнорирует остальную информацию в подграфе, то есть оставшиеся узлы и ребра.

Вместо этого извлечем все возможные сквозные пути и проверим каждый вариант с акцентом на соответствующие настройки роторов управления, полностью игнорируя настройки индексных роторов.

Далее исследуем влияние настроек роторов индекса в сочетании с логиками ввода и вывода индекса. В модели CSP-889 логика ввода индекса генерирует девять битов (фактически 10, но один всегда неактивен), и от одного до четырех из этих девяти битов активны. Роторы индекса в сочетании с логикой вывода индекса реализуют одностороннюю функцию, которая преобразует эти девять битов в пять, которые формируют шаблон управления роторами шифратора. Это сопоставление является постоянным и никогда не меняется, поскольку роторы индекса не меняют положения во время шифрования или дешифрования. Рассмотрим следующий пример:

1. В позиции i зашифрованного текста логика ввода индекса выдает 000110001.

2. В позиции i зашифрованного текста последовательность шагов ротора шифрования равна 00101 (что означает, что роторы индекса и логика вывода индекса отображают 000110001 на 00101).

3. В позиции j ≠ i зашифрованного текста логика ввода индекса также выдает 000110001.

Поскольку отображение является постоянным, мы ожидаем, что пошаговый шаблон в позиции j также будет 00101.

Преимущество постоянного отображения можно использовать при оценке сквозного пути в сравнении с заданной настройкой управляющего ротора путем проверки согласованности отображения между 9-битными выходными сигналами логики ввода индекса и 5-битным выходом логики вывода индекса.

Если один и тот же конкретный 9-битный вывод входной логики индекса в различных позициях в зашифрованном тексте не всегда отображается на один и тот же 5-битный пошаговый шаблон, мы можем исключить комбинацию пути и конкретных параметров тестируемых управляющих роторов. Если тест не пройден для всех возможных настроек управляющего ротора, мы можем полностью исключить путь. Таким образом, мы можем полностью протестировать путь, созданный на первом этапе, только проверив все возможные 2^35.4 настройки управляющих роторов и проигнорировав настройки индексных роторов.

Проведенные симуляции со случайными путями и настройками управляющего ротора, с измерениями минимального количества позиций зашифрованного текста, необходимого для обнаружения (первого) противоречия и исключения комбинации пути и настроек управляющего ротора дали следующие результаты (для 10 млн. симуляций):

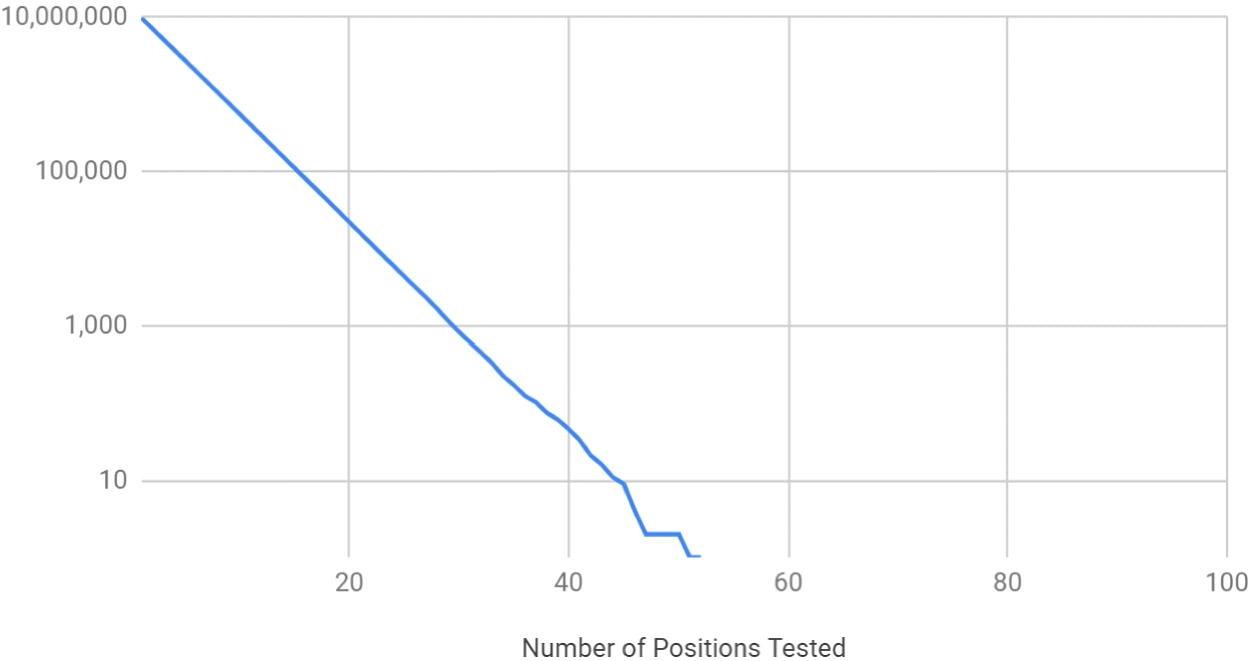
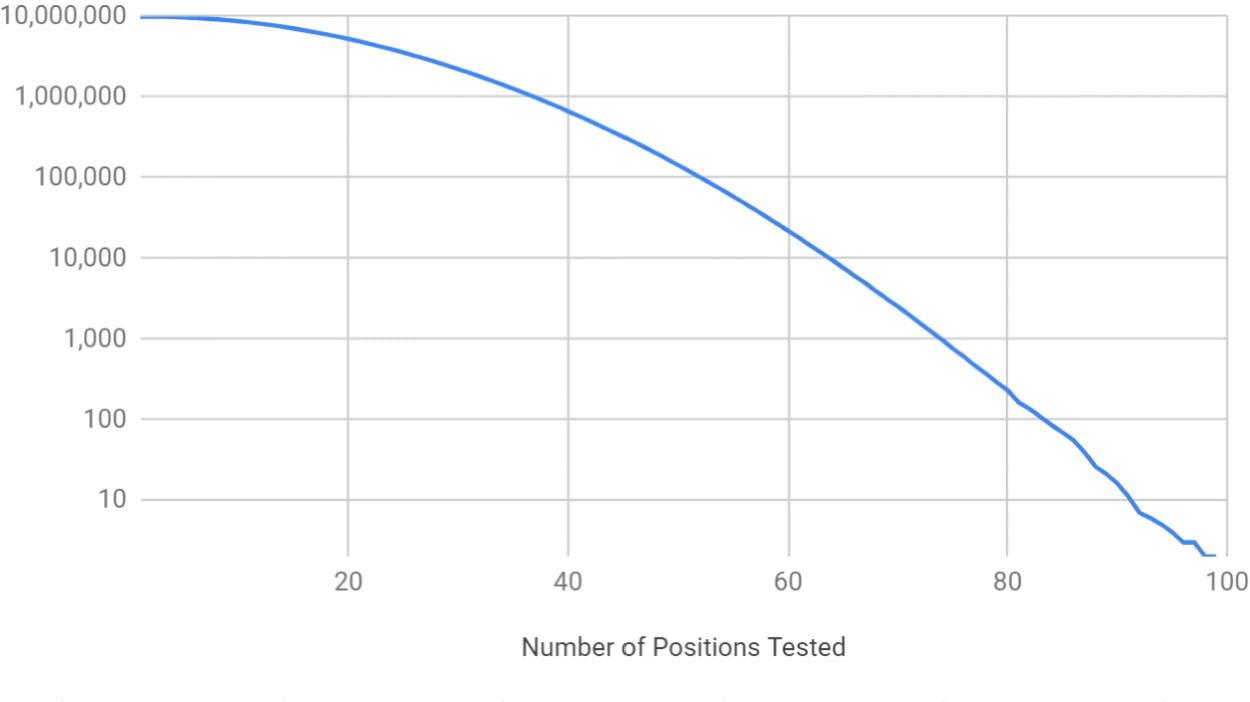
Для результатов CSP-889 можно заметить, что после тестирования всего 55 позиций можно исключить все неправильные комбинации.

Для CSP-2900 требуется 100 позиций зашифрованного текста, чтобы исключить неправильную комбинацию, что больше, чем требуется для CSP-889. Это можно объяснить тем, что в модели CSP-889 имеется четыре активных входа логики ввода индекса, которые генерируют 10-битный ввод для роторов индекса (подключено только девять). В модели CSP-2900 имеется шесть активных входов для входной логики индекса, так что количество возможных состояний 10-битного входа для индексных роторов значительно больше. Предложенный алгоритм ищет противоречия в позициях зашифрованного текста, которые имеют одинаковые 10-битные значения. Тем не менее, вероятность найти такие позиции ниже, если количество вариантов больше.

Если вариант пути проходит тест с определенной настройкой управляющего ротора, мы получаем многообещающий вариант решения, который остается проверить всего на 113400 конфигурациях роторов индекса, чтобы убедиться, что зашифрованный текст правильно расшифрован в одной из этих конфигураций.

2. Тестирование подграфов вместо путей.

Алгоритм первой оптимизации, описанный выше, требует только тестирования каждого пути, но он должен применяться ко всем сквозным путям, полученным на первом этапе атаки. Как видно из топологии даже простейшего графа (рис. 15), в нескольких позициях в последовательности зашифрованного текста, существует больше одной допустимой позиции ротора шифрования, которая правильно расшифровывает символы. В результате количество различных сквозных путей увеличивается экспоненциально для каждого узла (позиции), из которого есть несколько продолжений. Этот экспоненциальный взрыв еще мощней для более сложной (но и более вероятной) топологии графа.

Чтобы нивелировать этот экспоненциальный взрыв сквозных путей, модифицируем алгоритм, чтобы он мог обрабатывать все сквозные пути в подграфе, с помощью одного теста.

Во-первых, проигнорируем первые и последние десять уровней графа в подграфе, поскольку промежуточные уровни будут состоять из меньшего количества узлов (подобная ситуация наблюдается в примере, показанном на рисунке 17).

Во-вторых, расширим алгоритм, таким образом, чтобы его входными данными был не путь, где имеется только один узел на уровень (позицию) зашифрованного текста и одно ребро между двумя соседними уровнями, а набор возможных пошаговых шаблонов между узлами на уровне i (положения шифровального ротора в позиции зашифрованного текста i) и узлами на уровне (i + 1) (положения шифровального ротора в позиции зашифрованного текста (i + 1)). Если истинный путь содержится в подграфе, ожидаем, что правильный шаблон шага из позиции i будет включен в набор шаблонов для перехода из слоя i в слой (i + 1). 

Для каждого подграфа проверяем наборы на соответствие всем возможным настройкам управляющего ротора. Аналогично предыдущей оптимизации, ищем противоречия в появлении одного и того же 9-битного вывода из входной логики индекса в разных позициях зашифрованного текста, скажем, i  и j. Роторы индекса в сочетании с логикой вывода индекса всегда будут преобразовывать те же 9 бит в один и тот же 5-битный шаблон шага шифрования, поскольку роторы индекса не меняют положения.

Ранее при поиске несоответствий в отдельных путях нужно было только проверить, равны ли пошаговые шаблоны в позициях i  и j на пути. Здесь вместо этого мы тестируем вместе несколько путей, содержащихся в подграфе. Если один и тот же 9-битный вывод логики ввода индекса встречается в разных позициях зашифрованного текста, i  и j, и подграф содержит правильный путь, набор возможных шаблонов шагов для i (между i и (i + 1)) и набор возможных шаблонов для j (между j и (j + 1)) должен иметь, хотя бы один общий шаблон. Если это не так, то либо ни один из путей в подграфе не является правильным, либо настройки ротора управления несовместимы с подграфом и связанной с ним настройкой ротора шифрования.

Оценка этой оптимизации для большого количества смоделированных сценариев для CSP-889 показала, что при менее чем 60 символов зашифрованного текста все еще возможно исключить все неправильные подграфы. Для CSP-2900 необходимо применять дополнительные методы отбора, которые выходят за рамки статьи.

Если проверка подграфа на конкретную настройку ротора управления проходит успешно, появляется перспективный вариант, для проверки которого извлекаем все начальные позиции ротора шифрования из подграфа и, используя тестируемые настройки ротора управления, проверяем для всех возможных настроек ротора индекса, можно ли расшифровать зашифрованный текст так, чтобы он соответствовал ожидаемому открытому тексту.

3. Одновременное тестирование нескольких подграфов.

В предыдущей оптимизации для CSP-889 было обработано 80 внутренних позиций зашифрованного текста для проверки подграфа второго этапа, в то время как 60 из них уже было достаточно (см. рис.12), чтобы исключить неправильные подграфы или неправильные настройки управляющего ротора. Теперь мы воспользуемся дополнительными неиспользованными 20 позициями, чтобы ускорить второй этап атаки. Для этого будем тестировать несколько подграфов вместе, при условии, что одни и те же настройки ротора управления относятся ко всем подграфам, которые были созданы одним и тем же запуском первого этапа, т.е. при одних и тех же настройках роторов шифратора. Объединение нескольких подграфов, совместно использующих одну и ту же конфигурацию банка роторов шифрования, происходит путем слияния для каждой позиции i  наборов возможных шаблонов шагов на уровне i каждого подграфа.

Для CSP-889 объединение до восьми подграфов и их одновременное тестирование с помощью второй оптимизации, описанной выше, дает однозначные результаты при обработке только 80 внутренних позиций. Если тест для связки прошел успешно, все равно необходимо протестировать каждый отдельный подграф. Для CSP-2900 одновременное тестирование эффективно при объединении не более четырех подграфов.

Оценка эффективности

Алгоритмы первого и второго этапов очень сложны. Оба разработаны, начиная с упрощенных реализаций, улучшенных за счет ряда оптимизаций, сокращающих время их выполнения и улучшающих эффективность для использования их на персональных компьютерах (чтобы было понятно, система все равно должна быть очень мощная, здесь имеется в виду, что для вычислений не требуется специализированного оборудования, ниже конфигурация стенда). Полная аналитическая оценка алгоритмов сама по себе также является сложной задачей. В процессе оценки было измерено время работы на ПК с 64-ядерным процессором AMD Ryzen Threadripper 3990X с максимальной частотой в турбо режиме 4,3 ГГц, материнской платой Gigabyte TRX40 AORUS Extreme и 256 ГБ ОЗУ. Также необходимо отметить, что данные об успешности атаки носят статистический характер и не дают 100% гарантированного успеха, тем более существуют отличия для обеих моделей SIGABA, зависящие от конструктивных особенностей моделей аппаратуры шифрования.

На первом этапе необходимо обработать конфигурации роторов шифрования, то есть их выбор, порядок и настройки направления (аверс\реверс). На стенде, описанном выше, с 64 потоками, работающими параллельно, можно обрабатывать от 17 до 22 конфигураций в секунду, что требует от 12 до 16 часов для проверки всех конфигураций.

На втором этапе обрабатываются подграфы, созданные на первом этапе. Сначала они сортируются в соответствии с их оценкой, возможно, объединяются в группы для одновременной обработки и помещаются в очередь приоритетов переменной длины. Ожидается, что подграф, содержащий правильный сквозной путь, будет оценен так, что станет одним из подграфов с самым высоким рейтингом. Второй этап требует примерно 30 секунд для проверки одного подграфа, созданного на первом этапе.

Оценка производительности для модели CSP-889

На рисунке 14 показано среднее ожидаемое количество случайных подграфов для каждого порогового значения, превышающее это пороговое значение, и время (в часах), необходимое для проверки их всех, для CSP-889 и n = 100 символов известного открытого текста на основе большого количества итераций. Если оценка правильного подграфа выше этого предела, то после теста всех подграфов с оценкой выше этого предела, получим верное решение. Например, при пороговом значении —1.46 ожидается, что в среднем 1206 случайных подграфов, созданных на первом этапе, превысят этот предел.

Чтобы проверить их все, требуется около десяти часов, и вероятность того, что подлинный подграф имеет оценку выше этого предела, составляет 83.4%. Следовательно, вероятность успеха при пороговом значении —1.46 составляет 83.4%. Поскольку первый этап занимает от 12 до 16 часов, добавление десяти часов для второго этапа увеличивает общее время обработки примерно до 24 часов, опять же, с вероятностью успеха примерно 83.4%. И это самый негативный исход.

Также можно выделить некоторое количество ядер для параллельного выполнения второго этапа. Если один из подграфов выделится высокой оценкой, он окажется в верхней части приоритетной очереди, и будет обрабатываться на втором этапе почти сразу, как только появится, за счет чего можно сократить время вычислений.

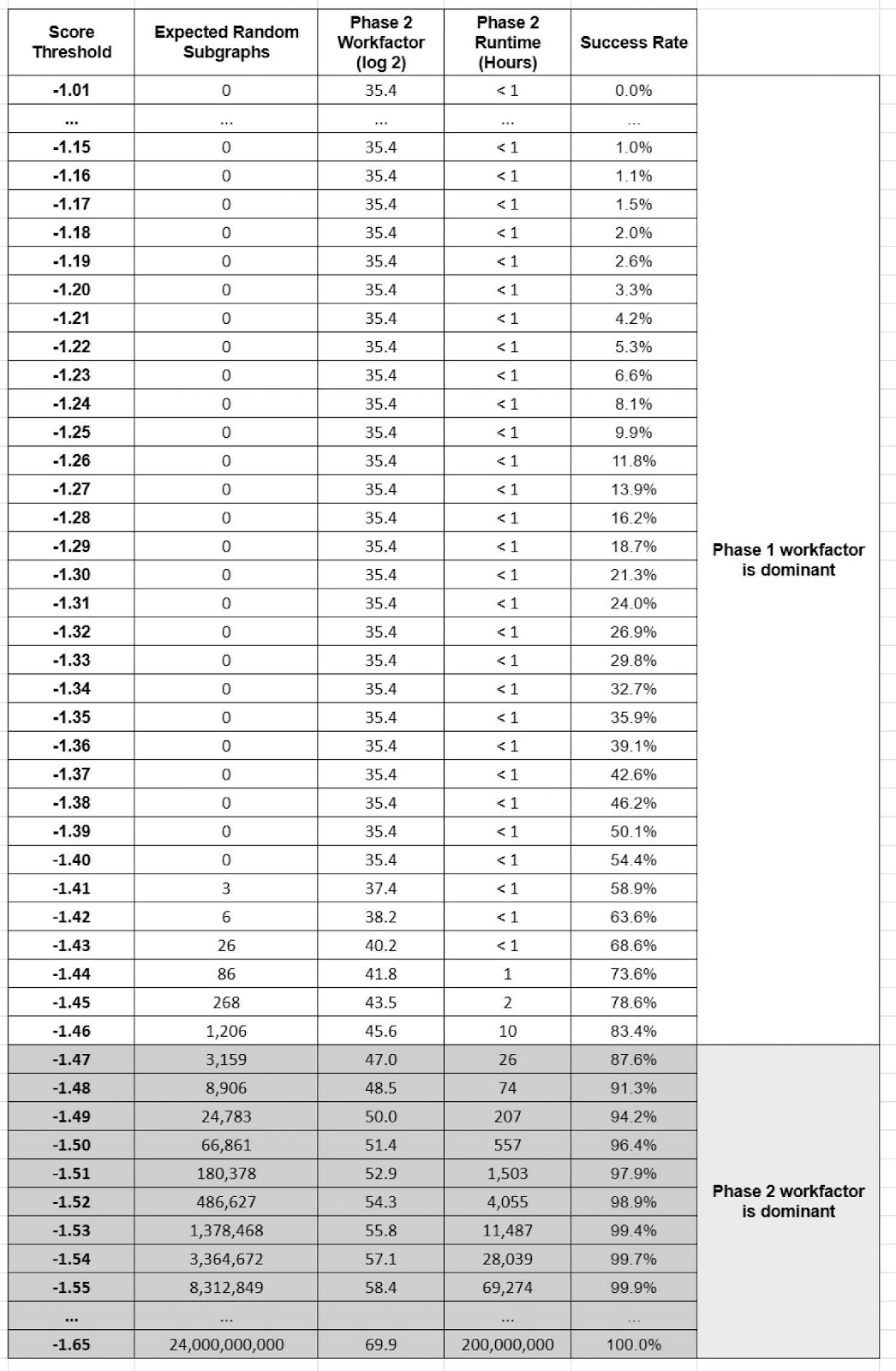
Достижение 100% гарантированного успеха для CSP-889 нецелесообразно. Вероятно, такой результат требует предела –1.65, и количество случайных подграфов, превышающих это пороговое значение, чрезвычайно велико. Можно заметить, что при каждом уменьшении предела на 0.01 количество случайных подграфов, генерируемых на втором этапе, увеличивается более чем в два раза, а пороговое значение в –1.65, вообще является экстраполяцией.

Хотя для второго этапа есть возможность вычислить предел аналитически (2^35.4 × r, где r — количество случайных/неправильных подграфов, сгенерированных на первом этапе с оценкой выше заданного предела), сделать это для первого этапа сложнее. Проще сравнить время выполнения этапов и определить, какой из них является доминирующим. Исходя из измеренного времени выполнения при пороговом значении –1.47  и меньше второй этап становится доминирующим, при значении большем –1.46 — первый этап.

При пороговом значении –1.47  с коэффициентом работы 2⁴⁷ для второго этапа (доминирующий коэффициент в целом для этого порогового значения) вероятность успеха составляет 87.6%. Для сравнения, полный перебор потребует 2^95.6 расшифровок, а двухэтапная неоптимизированная атака с вероятностью успеха в 82% может быть достигнута с коэффициентом 2^84.5. По сравнению с этим предложенный оптимизированный алгоритм атаки работает с суммарным коэффициентом 2^37.5. Это улучшение достигается следующим образом:

— второй этап требует только проверки возможных настроек управляющего ротора и не требует проверки всех настроек индекса, оставляя сложность вычислений на том же уровне;

— оставшуюся экономию можно объяснить тем, что на первом этапе агрессивно отфильтровываются пути/параметры с низкой вероятностью, поэтому на втором этапе необходимо проверить значительно меньшее количество вариантов, при этом обеспечивая сопоставимую (и даже немного более высокую) вероятность успеха.

Также если принять требуемый результат атаки за 100%, то модифицированный алгоритм атаки демонстрирует лучшие показатели 2^69.9 против 2^86.7, что объясняется тем фактом, что в предложенном алгоритме второй этап не требует тестирования всех настроек индекса.

Интересно сравнить производительность новой атаки с алгоритмом, имеющим 100% вероятность успеха, рабочий коэффициент 2^60.2 и требующим всего восьми известных символов открытого текста. Понятно, что при 100% требованиях расшифровки, лучше использовать этот метод. С другой стороны, такую атаку невозможно реализовать на одном неспециализированном ПК, в отличие от предложенного алгоритма при наличии длинного сегмента известного открытого текста и вероятности успеха порядка 90% или ниже.

Оценка производительности модели CSP-2900

При работе с моделью CSP-2900 и n = 100 на первом этапе не генерируется ни одного случайного подграфа выше порогового значения –1.42, и в очень большом количестве симуляций (1 млрд.) ни один из подлинных подграфов не получил оценку ниже этого порога. Как правило, на втором этапе нужно протестировать только один подходящий подграф. Таким образом, коэффициент работы на втором этапе незначителен, общее время обработки составляет от 12 до 16 часов для первого этапа, а вероятность успеха составляет 100%.

Необходимы дополнительные исследования оценки производительности этой атаки модели CSP-2900 с менее чем n = 100 известных символов открытого текста, а также определение вероятностей успеха при различных продолжительностях вычислений и рабочих коэффициентах второго этапа.

Историческая значимость

Основные уязвимые места, раскрытые в этой статье, важны в историческом контексте. Размер пространства ключей SIGABA – 2^95.6, но обнаруженные уязвимости позволяют проводить статистические атаки с рабочим коэффициентом 2⁴⁷. Вполне вероятно, что вычислительная технология, необходимая для выполнения атаки, была недоступна в 1940-х годах. Такая атака могла быть осуществима с помощью мощных мейнфреймов 1960-х или суперкомпьютеров 1970-х, после того как SIGABA была заменена более совершенными системами. 

До сих пор удивительно, что эти уязвимости не учитывались при разработке первых моделей аппаратуры, включая CSP-889. Еще более удивительно, что модификации более поздней модели CSP-2900 сделали SIGABA еще более уязвимой для статистических атак.

Одной из основных задач при разработке безопасных криптосистем является удаление любых неслучайных шаблонов. В то время как статистика частоты символов в зашифрованном тексте относительно плоская и распределена случайным образом.

Более того, сильная современная криптосистема должна быть невосприимчива к атакам типа «разделяй и властвуй». Разделение функций между банками роторов, является уязвимостью, открывающей двери для подобных атак. Этой уязвимости можно было бы избежать, если бы степпинг роторов шифрования зависел не только от роторов управления и индекса, но и от самого шифратора.

Заключение

SIGABA считается самым безопасным шифровальным устройством, использовавшимся союзниками во время Второй мировой войны. Нет никаких доказательств того, что немецкие криптоаналитики сумели взломать эту аппаратуру. В 2007 году впервые была представлена атака на SIGABA по принципу «разделяй и властвуй», которая, хотя и ненамного более эффективна, чем поиск методом грубой силы, заложила основу для значительных дальнейших модернизаций алгоритмов взлома.

В 2019 году была проведена атака по известному открытому тексту всего из 8 букв (n = 8) с использованием вычислительной мощности, сравнимой с той, которая требуется для восстановления 56-битного ключа алгоритма симметричного шифрования DES.

Методы и результаты, описанные в статье, демонстрируют, что SIGABA подвержена мощной статистической атаке с известным открытым текстом, для которой требуется n = 100 букв и рабочим коэффициентом 2⁴⁷, с вероятностью успеха 87.6%. Эта атака может быть проведена менее чем за 24 часа на мощном потребительском ПК. С другой стороны, современные методы, включая описанный, не могли быть применены на базе технологий 1940-х или 1950-х годов. Любопытно, что модификации, внесенные в более позднюю версию аппаратуры шифрования CSP-2900, снизили ее защищенность от описанной здесь атаки.

Топология графов первого этапа

На рисунках отмечено только положение выбранных узлов на начальном и конечном уровнях. Ребра подписаны номерами роторов шифрования, которые шагают (например, 245 означает, что роторы 2, 4 и 5 изменили положение). Путь, отмеченный красным, представляет собой настоящий путь, а путь, отмеченный оранжевым, путь с наивысшей оценкой (остальные узлы отмечены черным цветом). Правильный путь обычно имеет наивысший балл, но не всегда.

На рис. 15 показана простая топология только с одним подграфом, включающим несколько объединенных путей. Правильный путь также является самым высокоранговым. Однако хотя имеется только одна начальная позиция и одна конечная позиция, существуют слои, в которых имеется более одной позиции.

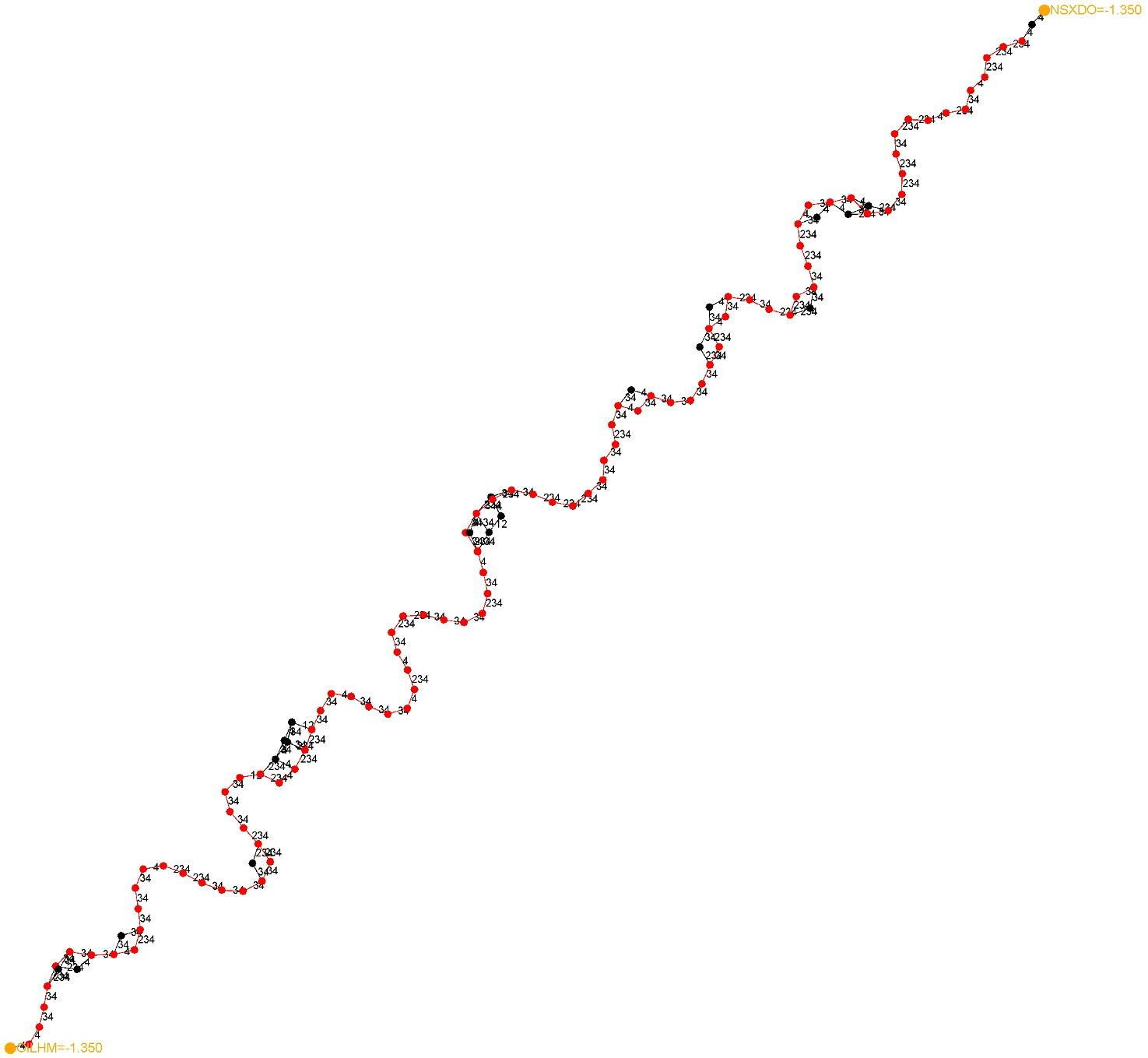
На рис. 16 показана несколько более сложная топология с двумя подграфами, причем тот, который включает правильный путь, не является самым высокоранговым. Кроме того, в каждом подграфе имеется более одной начальной и конечной позиции.

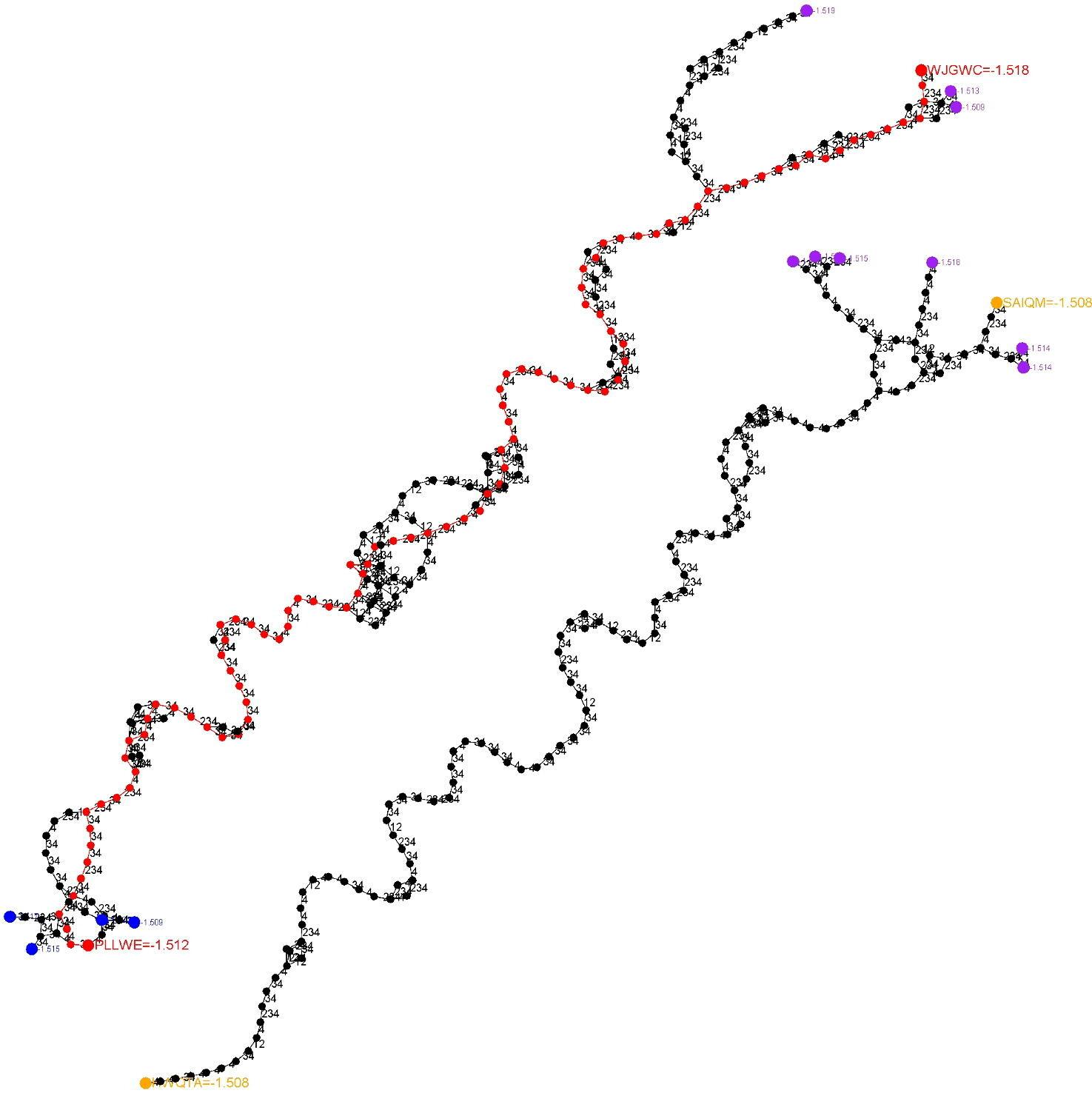
На рис. 17 показана еще более сложная топология, по-прежнему всего один подграф, включающий множество сливающихся путей, но с множеством начальных и конечных позиций.

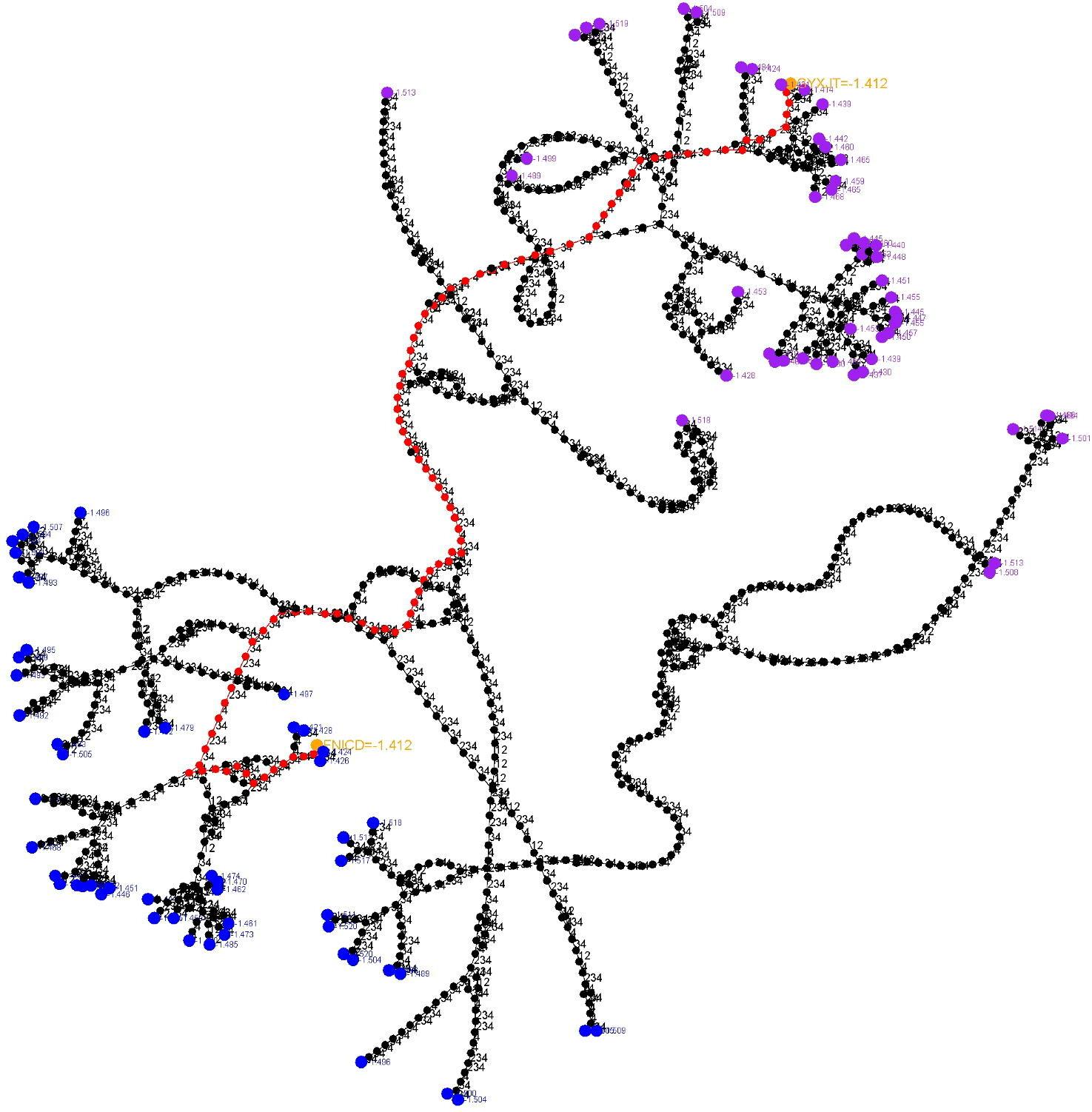
На рис. 18 показана очень сложная топология с большим количеством подграфов.

Автор исследования:

Джордж Ласри — ученый из Израиля, участник проектов DECRYPT и CrypTool. Имеет докторскую степень. Основной интерес в криптографических исследованиях заключается в применении специализированных методов оптимизации для компьютеризированного криптоанализа классических шифров и шифровальных машин. В 2013 году решил задачу шифра Double Transposition (Doppelwurfel). Также расшифровал немецкие шифрованные тексты ADFGVX и дипломатические коды времен Первой мировой войны; сообщения времен Второй мировой войны, зашифрованные с помощью немецкого шифровального устройства Siemens and Halske T52; коллекцию папских шифров 16, 17 и 18 веков; и шифры перестановки времен Биафранской войны в конце 1960-х годов.

---

НЛО прилетело и оставило здесь промокод для читателей нашего блога:

— 15% на все тарифы VDS (кроме тарифа Прогрев) — HABRFIRSTVDS.