Некоторое время назад в ходе определенных рассуждений, явно не связанных с архитектурами искусственных нейронных сетей, у меня возникла, скажем так, гипотеза, которая могла бы объяснить, почему в свое время skip connections смогли произвести своего рода революцию в развитии глубокого обучения и позволили строить действительно глубокие нейронные сети. С тех пор много воды утекло, но все современные SOTA архитектуры являются в той или иной степени продолжением развития ResNet архитектур. Чего там говорить, даже в трансформерах есть skip connections. К сожалению, времени и сил на полноценное исследование нет и вряд ли найдется, а между тем идея кажется как минимум интересной с академической точки зрения, так и могущей возыметь практический выхлоп, а потому я бы хотел поделиться ею, по крайней мере, с аудиторией хабра. Буду краток.

Для решения какой проблемы были введены skip connection в residual архитектурах?

Это один из вопросов, который можно услышать на собеседованиях на позицию ML-инженеров. По крайней мере, именно в такой формулировке мы в нашей компании задаем его соискателям на предварительном скрининг-собеседовании, и, согласно их отзывам, это один из весьма популярных и часто встречаемых вопросов. При этом абсолютное большинство соискателей отвечают на него… неправильно. Лишь немногим отличаясь, ответы в большинстве своем звучат примерно следующим образом: "для решения проблемы затухающего градиента". И это действительно неправильный ответ: заглянув в оригинальную статью, мы увидим, буквально на первой же странице во введении, следующие строки:

Driven by the significance of depth, a question arises: Is learning better networks as easy as stacking more layers? An obstacle to answering this question was the notorious problem of vanishing/exploding gradients [1, 9], which hamper convergence from the beginning. This problem, however, has been largely addressed by normalized initialization [23, 9, 37, 13] and intermediate normalization layers [16], which enable networks with tens of layers to start converging for stochastic gradient descent (SGD) with backpropagation [22].

И ведь действительно, если вдуматься, наличие слоев нормализации должно позволять градиенту течь по сети без затухания. И хоть skip connections (a.k.a. shortcut connections) в принципе изначально были предложены еще до появления ResNet архитектуры, в том числе для решения проблемы затухающего градиента (что, возможно, и служит причиной столь широко распространенного заблуждения), в ResNet архитектурах они в действительности помогли решить другую проблему - проблему деградации точности (о чем в статье говориться буквально в следующем абзаце). Проблема деградации точности заключается в том, что при увеличении глубины сети точность сначала возрастает, потом, вопреки ожиданиям, выходит на плато, а после даже начинает снижаться вплоть до полной потери способности сети к обучению. Существует довольно популярное мнение (вероятно, среди тех, кто читал/помнит оригинальную статью и знает, что затухание градиента тут ни при чем), что: skip connection в residual архитектурах помогают модели выучить тождественное преобразование - таким образом, имея возможность пропускать сигнал без трансформаций, модель должна, по крайней мере, быть не хуже, чем ее менее глубокая версия, следовательно, деградировать точность не может. Подобное объяснение действительно имеет место быть, но оно носит, так сказать, симптоматический характер. А что, если копнуть глубже и попытаться разобраться, в чем вообще причина такого явления, как деградация точности глубокой нейронной сети при увеличении ее глубины? Разумеется, можно начать рассуждать про увеличение размерности параметрического пространства, про ухудшение сходимости, про застревание в локальных минимумах в процессе оптимизации и так далее, однако добавление skip connections не снижает размерность параметрического пространства. Стало быть, сама по себе высокая размерность не является причиной деградации точности. А что же тогда?..

Симметрия в нейронных сетях

Причиной (многих) проблем глубокого обучения и подсказкой к поиску путей их решения может являться симметрия параметрического пространства. Именно параметрического, а не признакового, т.е. речь не идет о симметрии входных образов, как то симметрии отражения или поворотов, которыми могут обладать, например, некоторые классы изображений. Нет, речь в данном случае идет об инвариантности результата работы сети по отношению к некоторым операциям, действующим в пространстве параметров нейронной сети:

где - некоторое линейное преобразование в пространстве параметров .

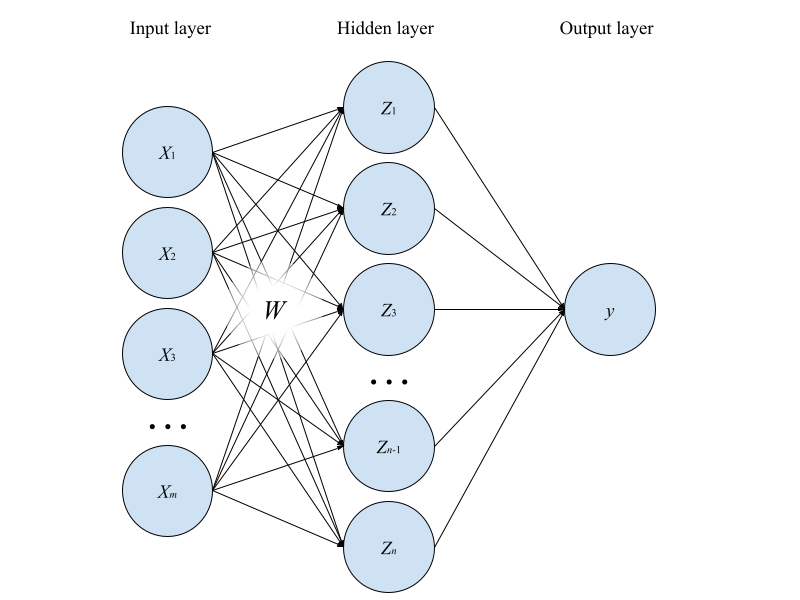
Для простоты рассуждений возьмем полносвязную сеть с одним скрытым слоем (рис. 1). Рассмотрим, для начала, случай, когда все веса выходного линейного слоя фиксированы и равны , т.е. последний слой выполняет роль простого арифметического усреднения выходов нейронов скрытого слоя. Параметры же скрытого слоя удобно представить в виде прямоугольной матрицы размера , где - размерность входного слоя, - размерность скрытого слоя (для простоты, но не нарушая общности рассуждений, забудем про смещение, a.k.a. bias). Таким образом, результат работы сети можно представить в виде:

Что произойдет с результатом работы сети, если мы поменяем местами, скажем, первый и второй нейроны скрытого слоя? Очевидно, что при такой перестановке результат работы сети не изменится. При этом такая операция меняет местами первую и вторую строки матрицы весов скрытого слоя. Т.е. до и после перестановки мы имеем две, вообще говоря, разные матрицы весов, дающие один и тот же результат на выходе сети. Более того, переставить местами мы можем любые два нейрона (любые две строки матрицы ) - результат работы сети инвариантен к любым таким перестановкам, а всего вариантов перестановок Таким образом, как минимум наборов весов (точек в параметрическом пространстве) являются эквивалентными в смысле результата работы сети, независимо ни от входных данных, ни от функций активации и т.д. Это утверждение справедливо не только в рассмотренном нами случае, но и в общем случае, с той лишь разницей, что перестановка i-ого и j-ого нейронов l-го слоя представляет собой перестановку i-й и j-й строки матрицы вместе с перестановкой i-го и j-го столбцов матрицы -го слоя. Из этих рассуждений мы можем заключить, что один полносвязный слой задает в пространстве параметров степень симметрии, по крайней мере, не ниже, чем , а степень симметрии параметрического пространства всей сети равна произведению степеней симметрии каждого слоя, т.е. , поскольку перестановки нейронов в двух слоях выполняются независимо друг от друга. Таким образом, мы определили возможный вид преобразования из выражения 1 - перестановочная матрица. Сразу отмечу, что перестановка - не единственная возможная операция симметрии в пространстве параметров, и в зависимости от используемой нелинейности результат работы сети может оказаться инвариантен и к некоторым другим преобразованиям, специфичным для этой нелинейности (особенно широкий простор для симметрий, в т.ч. непрерывных, обеспечивает ReLU).

Проблемы сходимости, связанные с высокой степенью симметрии признакового пространства, могут возникать на гиперповерхностях симметрии - многообразиях в параметрическом пространстве, точки которых инвариантны к соответствующим операциям симметрии. Например, если две строки в матрице весов равны друг другу, то их перестановка местами не приводит к изменению не только результата, но и самого вектора параметров - такая точка в параметрическом пространстве лежит на одной из плоскостей симметрии. Для наглядности рассмотрим наиболее простой возможный пример (пусть и нарочито игрушечный):

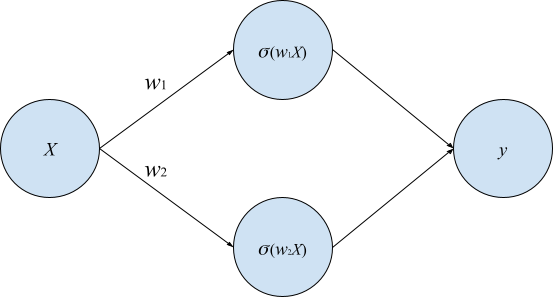
Поскольку здесь всего два варьируемых параметра, мы можем изобразить ландшафт функции потерь на плоскости с использованием любого удобного представления, скажем, contour plot (рис. 3).

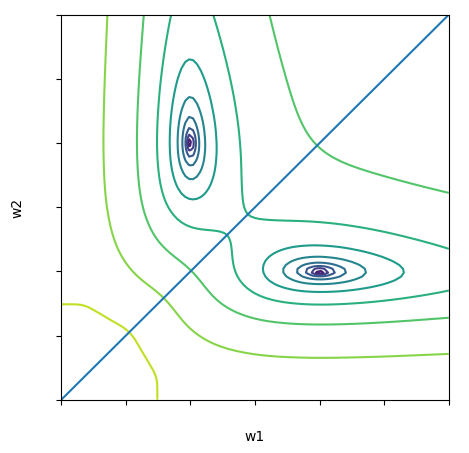
Как мы видим, функция потерь, имеющая два эквивалентных минимума, симметрична относительно прямой , или, правильнее в угоду общности будет сказать, относительно 1d-гиперплоскости, задаваемой вектором нормали (1, -1). Собственно, это и есть пример гиперповерхности симметрии, упомянутой ранее. Любая точка, принадлежащая этой прямой, является инвариантной относительно операции симметрии, благодаря которой функция потерь имеет два минимума. Так вот, важно здесь то, что на этой самой поверхности, в общем случае, вдоль ортогональных плоскости направлений функция потерь имеет локальный экстремум, который может быть как максимум, так и минимумом. Назовем такой минимум ложным, поскольку в общем случае он не является оптимальной точкой решения задачи оптимизации, а обусловлен свойствами параметрического пространства модели. 

Картина усложняется, когда мы имеем множество пересекающихся гиперповерхностей в результате стекинга нескольких слоев - ландшафт функции потерь может усложняться чрезвычайно сильно - вероятность возникновения ложных минимумов повышается с увеличением степени симметрии параметрического пространства, которая, в свою очередь, растет катастрофически с увеличением глубины и ширины сети. Больше локальных минимумов - больше вероятность застрять в этих минимумах в процессе оптимизации. Собственно, основная гипотеза, выдвигаемая на основании всех этих рассуждений, состоит в том, что проблема деградации точности связана с ростом числа локальных минимумов при увеличении глубины сети, обусловленным ростом степени симметрии параметрического пространства. 

И тут на помощь приходят skip connections

Так чем же тогда помогают skip connections? Тут все достаточно просто и Вы, возможно, уже догадались сами: skip connections существенно снижают симметрию параметрического пространства, уменьшая, тем самым, число локальных минимумов и облегчая сходимость. Если это утверждение не кажется столь очевидным, достаточно рассмотреть уже знакомый нам пример полносвязной сети, чтобы его понять. Добавим в сеть, изображенную на рисунке 1, skip connections между входом и выходом первого слоя (правда, для этого нам потребуется сделать размерность выхода равной размерности входа, но сути это не меняет).

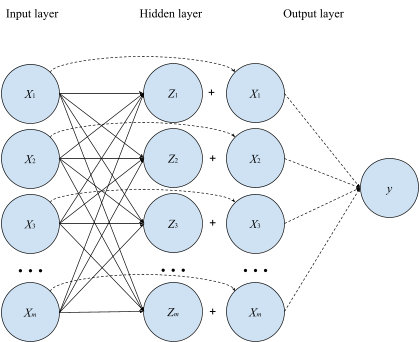
Поскольку перестановка местами двух нейронов в слое не зависит от его входа, то в этот раз мы уже не можем переставлять местами нейроны в скрытом слое, не меняя выход сети, поскольку он зависит уже не только от весов скрытого слоя, но и входного значения, с которым суммируется активация. Т.е., добавив skip connection, причем, именно аддитивный (подойдет также, например, мультипликативный, но не конкатенативный), мы снизили степень перестановочной симметрии слоя с до 1! Таким образом, добавление skip connections по всей глубине сети позволяет значительно снизить степень симметрии параметрического пространства, а, значит, и число локальных минимумов функции потерь, делая ее ландшафт более "хорошим" для оптимизации.

Примечание

Как верно заметил @maty, в том случае, когда все веса последнего слоя одинаковы, перестановка местами нейронов в скрытом слое даже при наличии skip connections не приведет к изменению результата сети:

Однако в общем случае это не так, т.е. пространство параметров симметрией относительно перестановки нейронов в слое со skip connections не обладает ( и - веса последнего слоя):

После проведенных рассуждений не грех задаться вопросом: если skip connections действительно помогает решить проблему деградации точности за счет снижения симметрии параметрического пространства, то что еще может обладать подобным свойством? Рискну предположить, что к приемам, которые исторически помогли решить ту или иную проблему при дизайне новых нейросетевых архитектур, действительно можно отнести несколько, в частности: групповую (в пределе - поканальную) свертку (group and depth-wise convolutions), позиционное кодирование (positional encoding), dropout. Первые два приема, в ретроспективном рассмотрении, обладают тем свойством, что помогают в целом снизить степень симметрии параметрического пространства как и skip connections. Так, например, depth-wise convolution, используемая для факторизации операции свертки, с одной стороны, разумеется, позволяет снизить размерность параметрического пространства (что оказывается важным для инференса на устройствах), но также и снижает степень симметрии, поскольку каждый канал теперь обрабатывается своим фильтром, и, следовательно, результат работы сети уже не инвариантен к перестановкам ядер.

Что касается регуляризации dropout, то ее можно связать с симметрией следующим образом: отключение случайного подмножества нейронов на каждом шаге обучения локально (на данном шаге) нарушает симметрию признакового пространства, т.е. у оптимизатора появляется шанс пройти мимо ложного минимума, обеспеченного симметрией ландшафта функции потерь на гиперповерхностях симметрии или их пересечении.

Что-нибудь еще? Возможно… Предлагаю заинтересовавшимся подумать над этим вместе.

Послесловие

Получилось, на мой взгляд, достаточно кратко. Возможно, изложенная идея кому-то покажется простой, очевидной или незначительной, другого может натолкнет на какие-то интересные мысли. В любом случае, приглашаю к обсуждению.