Недавно на Хабре вышла статья за авторством MilashchenkoEA , в которой автор восполняет обнаруженный им пробел в доступных материалах по методам построения кривых плотности распределения вероятности по имеющемуся набору числовых данных. Акцент в статье сделан на методическую сторону получения (оценки) плотности вероятности случайной величины, поэтому автор не преследует цели получения оптимального, с вычислительной точки зрения, алгоритма. Что ж, в данной заметке попытаемся исправить эту ситуацию, а также взглянем под другим углом на способ решения данной задачи.

Постановка задачи

Дан набор значений случайной величины , сэмплированный из некоторого непрерывного распределения. Необходимо оценить функцию плотности распределения вероятности случайной величины по заданной выборке. Для решения задачи можно использовать только нативные функции python; для построения графиков используется matplotlib; Pandas DataFrame используется как контейнер данных в соответствие с оригинальной статьей (хотя в общем-то можно обойтись и без него).

Подготовка данных

Тестировать методы будем с использованием данных, сгенерированных для 4-х распределений, для которых известны аналитические выражения плотности, как в оригинальной статье: Релея, гамма, Вейбулла и экспоненциального. Для этого используем код MilashchenkoEA с небольшими изменениями (для удобства дальнейшего использования изменены сигнатуры функций, возвращающих значения аналитической функции плотности вероятности на заданном массиве значений случайной переменной):

import random
import math
import matplotlib.pyplot as plt
import pandas
import pandas as pd
import numpy as np  # Понадобится для расчета метрик
from time import perf_counter  # Понадобится для определения времени выполнения


def rel_pdf(rel_sigma: float, X: list) -> pandas.DataFrame:
    """
    Вычисляет Релеевскую кривую плотности распределения вероятности по известной формуле
    :param rel_sigma: среднеквадратическое отклонение
    :param X: координаты по оси абсцисс
    :return: pandas.DataFrame
    """
    pdf_y = []  # Координаты по оси ординат
    for x in X:
        pdf_y.append(((2 * x) / rel_sigma) * math.exp((-x ** 2) / rel_sigma))
    return pd.DataFrame({'x': X, 'y': pdf_y})


def rel_rand(n: int, rel_sigma: float) -> list:
    """
    Генерирует случайные числа с Релеевской плотностью распределения вероятности
    :param n: количество отсчетов
    :param rel_sigma: среднеквадратическое отклонение
    :return: list
    """
    rel_list = []
    for i in range(n):
        rel_list.append((rel_sigma / math.sqrt(2)) * math.sqrt(-2 * math.log(random.uniform(0, 1))))
    return rel_list


def gam_pdf(v: float, b: float, X: list) -> pandas.DataFrame:
    """
    Вычисляет кривую плотности Гамма распределения вероятности по известной формуле
    :param v: параметр формы
    :param b: масштабный коэффициент
    :param X: координаты по оси абсцисс
    :return: pandas.DataFrame
    """
    pdf_y = []  # Координаты по оси ординат
    for x in X:
        pdf_y.append(((b ** v) / math.gamma(v) * (x ** (v - 1)) * math.exp(-b * x)))
    return pd.DataFrame({'x': X, 'y': pdf_y})


def gam_rand(n: int, v: float, b: float) -> list:
    """
    Генерирует случайные числа с гамма распределением плотности вероятности
    :param n: количество отсчетов
    :param v: параметр формы
    :param b: масштабный коэффициент
    :return: list
    """
    gam_list = [random.gammavariate(v, 1 / b) for i in range(n)]
    return gam_list


def weib_pdf(a: float, b: float, X: list) -> pandas.DataFrame:
    """
    Вычисляет кривую плотности распределения вероятности Вейбулла по известной формуле
    :param a: масштабный коэффициент
    :param b: параметр формы
    :param X: координаты по оси абсцисс
    :return: pandas.DataFrame
    """
    pdf_y = []  # Координаты по оси ординат
    for x in X:
        pdf_y.append((b / a) * ((x / a) ** (b - 1)) * math.exp(-(x / a) ** b))
    return pd.DataFrame({'x': X, 'y': pdf_y})


def weib_rand(n: int, a: float, b: float) -> list:
    """
    Генерирует случайные числа с распределением плотности вероятности Вейбулла
    :param n: количество отсчетов
    :param a: масштабный коэффициент
    :param b: параметр формы
    :return: list
    """
    wei_list = [random.weibullvariate(a, b) for i in range(n)]
    return wei_list


def exp_pdf(l: float, X: list) -> pandas.DataFrame:
    """
    Вычисляет кривую экспоненциальной плотности распределения вероятности по известной формуле
    :param l: обратный коэффициент масштаба
    :param n: количество рассчитанных точех
    :param X: координаты по оси абсцисс
    :return: pandas.DataFrame
    """
    pdf_y = []  # Координаты по оси ординат
    for x in X:
        pdf_y.append(l * math.exp(-l * x))
    return pd.DataFrame({'x': X, 'y': pdf_y})


def exp_rand(n: int, l: float) -> list:
    """
    Генерирует случайные числа с экспоненциальным распределением плотности вероятности
    :param n: количество отсчетов
    :param l: обратный коэффициент масштаба
    :return: list
    """
    exp_list = [random.expovariate(l) for i in range(n)]
    return exp_list

Сгенерируем для каждого распределения наборы случайных величин, и организуем их в словарь:

random_series = {
    'rrand': rel_rand(100000, 1),  # генерируем случайные числа с распределением Релея
    'grand': gam_rand(100000, 0.5, 0.5),  # генерируем случайные числа с гамма распределением
    'wrand': weib_rand(100000, 1, 5),  # генерируем случайные числа с распределением Вейбулла
    'exprand': exp_rand(100000, 1.5)  # генерируем случайные числа с экспоненциальным распределением
}

Далее, эти наборы данных будут использованы для тестирования целиком, либо срезами, содержащими значений случайной величины.

Оптимизируем алгоритм, основанный на бинаризации данных

В качестве алгоритма нахождения плотности распределения автор предлагает довольно широко распространенный метод, основанный на разбиении интервала значений переменной на заданное число бинов равной ширины и подсчет числа вхождений значений переменной в каждый бин, реализованный в ряде библиотек [numpy, scipy, pandas], а также собственную реализацию в соответствии с условиями (оригинальные комментарии сохранены):

def pdf_original(k: int, rnd_list: list) -> pandas.DataFrame:
    """
    Получает кривую плотности распределения вероятности
    :param k: количечиво интервалов разбиения гистограммы
    :param rnd_list: случайный процесс
    :return: pandas.DataFrame
    """
    pdf_x = []  # Координаты по оси абсцисс
    pdf_y = []  # Координаты по оси ординат
    n = len(rnd_list)  # количество элементов в рассматриваемой выборке
    h = (max(rnd_list) - min(rnd_list)) / k  # ширина одного интервала
    a = min(rnd_list)  # минимальное значение в рассматриваемой выборке
    for i in range(0, k):  # проход по интервалам
        count = 0
        for j in rnd_list:  # подсчет количества вхождений значений из выборки в данный интервал
            if (a + i * h) < j < (a + (i * h) + h):
                count = count + 1
        pdf_x.append(a + i * h + h / 2)  # координата по оси абсцисс полученной кривой плотности распределения
        # вероятности
        pdf_y.append(count / (n * h))  # координата по оси ординат полученной кривой плотности распределения
        # вероятности
    d = {'x': pdf_x, 'y': pdf_y}
    return pd.DataFrame(d)

Можно заметить, что сложность данного алгоритма составляет , т.к. внешний цикл пробегает значений, внутренний же, в худшем случае, пробегает значений. Грубо оценим время выполнения функции при различных значениях и

for k in [100, 1000, 10000]:
    tic = perf_counter()
    _ = pdf_original(k, rrand)
    print('%.3f s' % (perf_counter() - tic))

for N in [10000, 20000, 30000]:
    tic = perf_counter()
    _ = pdf_original(1000, rrand[:N])
    print('%.3f s' % (perf_counter() - tic))

Вывод:

0.726 s
7.006 s
69.418 s

0.783 s
1.429 s
2.145 s

Разумеется, столь удручающие результаты не позволяют использовать данную реализацию метода, благо есть готовые реализации. Однако, можно добиться линейной сложности алгоритма подсчета значений в бинах по и константной по , существенно, тем самым, снизив вычислительное время, всего лишь добавив предварительную сортировку значений и заменив внутренний цикл по всем значениям случайной величины на цикл лишь по тем значениям, которые попадают в бин:

def pdf_optimized(k: int, rnd_list: list) -> pandas.DataFrame:
    """
    Получает кривую плотности распределения вероятности
    :param k: количечиво интервалов разбиения гистограммы
    :param rnd_list: случайный процесс
    :return: pandas.DataFrame
    """
    pdf_x = []  # Координаты по оси абсцисс
    pdf_y = []  # Координаты по оси ординат
    n = len(rnd_list)  # количество элементов в рассматриваемой выборке
    h = (max(rnd_list) - min(rnd_list)) / k  # ширина одного интервала
    a = min(rnd_list)  # минимальное значение в рассматриваемой выборке
    rnd_list = sorted(rnd_list)  # сортируем значения
    j = 0  # индекс значения левой границы интервала 
    for i in range(0, k):  # проход по интервалам
            count = 0
        while j < n and (a + i * h) <= rnd_list[j] < (a + (i * h) + h):  # подсчитываем количество значений в k-м интервале
                count = count + 1
                j += 1
        pdf_x.append(a + i * h + h / 2)  # координата по оси абсцисс полученной кривой плотности распределения
        # вероятности
        pdf_y.append(count / (n * h))  # координата по оси ординат полученной кривой плотности распределения
        # вероятности
    d = {'x': pdf_x, 'y': pdf_y}
    return pd.DataFrame(d)

Выполним аналогичное тестирование времени выполнения оптимизированной функции при различных значениях и добавив некоторое число повторений:

N_repeats = 100
for k in [100, 1000, 10000]:
    tic = perf_counter()
    for _ in range(N_repeats):
        _ = pdf_optimized(k, random_series['rrand'])
    print('%.3f s' % ((perf_counter() - tic) / N_repeats))

for N in [25000, 50000, 100000]:
    tic = perf_counter()
    for _ in range(N_repeats):
        _ = pdf_optimized(10000, random_series['rrand'][:N])
    print('%.3f s' % ((perf_counter() - tic) / N_repeats))

Вывод:

0.035 s
0.034 s
0.039 s

0.013 s
0.021 s
0.038 s

С такими результатами гораздо приятнее иметь дело и такую нативную реализацию можно использовать в условиях, когда нет возможности устанавливать дополнительные пакеты. Следует, однако, заметить, что ассимптотическая сложность метода определяется алгоритмом сортировки, и в данном случае составляет .

Примечание:
Представленные выше реализации используют нестрогое равенство для сравнения действительных чисел, что, вообще говоря, некорректно. Вследствие этого могут возникать граничные эффекты, поскольку вхождения минимального/максимального значений случайной величины в первый/последний бины не гарантировано. Следует немного модифицировать реализацию, добавив учет по умолчанию минимального и максимального значений случайной величины в первом и последнем бинах, соответственно, и пробегать в цикле по оставшимся значениям.

Считаем плотность распределения через функцию распределения

Далее рассмотрим несколько иной подход к получению оценки плотности распределения случайной величины. Вспомним, что плотность распределения случайной величины представляет собой первую производную от функции распределения, которая, в свою очередь, является вероятностью обнаружить значение случайной величины меньше либо равное заданному. Для того, чтобы получить оценку функции распределения вероятности, а из нее, в свою очередь, плотность распределения, предлагается выполнить следующие шаги:

1. сортируем значения переменной по возрастанию, получаем набор отсортированных значений ;

2. ставим в соответствие каждому значению в массиве отсортированных значений его порядковый номер начиная с нуля — с точностью до множителя, представляет собой оценку функции распределения случайной величины (Рисунок 1, синяя кривая);

3. строим равномерную шкалу из значений на интервале от до где — желаемое число точек кривой плотности распределения () — аналог числа бинов в гистограмме;

4. интерполируем значения номеров переменных из шкалы упорядоченного массива значений переменной в равномерную шкалу, полученную в п. 3 (Рисунок 1, оранжевая кривая);

5. численно берем производную от интерполированной функции по соседним точкам (для этого и было нужно значений) и делим на — получаем, таким образом, искомую оценку плотности вероятности.

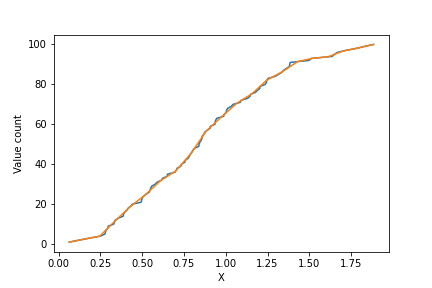
Ниже представлена реализация метода:

def pdf_custom(k: int, rnd_list: list):
    """
    Получает кривую плотности распределения вероятности
    :param k: количечиво интервалов разбиения гистограммы
    :param rnd_list: случайный процесс
    :return: pandas.DataFrame
    """
    X = sorted(rnd_list)  # сортируем значения случайной переменной
    N = len(X)
    i = 0
    dx = (X[-1] - X[0]) / (k + 2)  # находим шаг по аргументу в равномерной шкале
    result = []
    result_x = []
    for j in range(k + 2):  # пробегаем по точкам
        x = X[0] + j * dx  # находим соответствующее значение аргумента в равномерной шкале 
        result_x.append(x)
        while True:  # с помощью данного цикла находим индекс i такой, 
                     # что x лежит в пределах от X[i] до X[i+1]
            if x > X[i + 1]:
                i += 1
            else:
                break
        result.append(i + (x - X[i]) / (X[i + 1] - X[i]))
    norm = 0.5 / dx / N
    d = {
        'x': result_x[1:-1],
        'y': [(right - left) * norm for right, left in zip(result[2:], result[:-2])]}
    return pd.DataFrame(d)

Сложность представленного алгоритма также составляет . В результате тестирования времени выполнения получим следующие значения для = [100, 1000, 10000] при = 100 000 и = [25000, 50000, 100000] при = 10 000:

0.020 s
0.020 s
0.024 s

0.009 s
0.014 s
0.024 s

Новый метод оказался несколько быстрее, при той же алгоритмической сложности.

Сравниваем точность представленных методов

Для сравнения точности представленных методов будем использовать расстояние Кульбака-Лейблера от априорной функции плотности распределения до получаемой оценки :

Для вычисления метрики уже, не мудрствуя лукаво, будем использовать numpy:

def KL_dist(P: list, Q: list):
    assert len(P) == len(Q)
    eps = 1e-9
    P = np.asarray(P)
    Q = np.asarray(Q)
    return np.mean(P * (np.log(P + eps) - np.log(Q + eps)))

Получим оценки плотности распределения случайной величины для разных априорных распределений при разных соотношениях и сравним значений KL-дивергенции:

from functools import partial

pdf_function = {
    'rrand': partial(rel_pdf, 1),
    'grand': partial(gam_pdf, 0.5, 0.5),
    'wrand': partial(weib_pdf, 1, 5),
    'exprand': partial(exp_pdf, 1.5)
} 

N = 10000
k_values = np.logspace(2, 4, 10, dtype=np.int)

metrics_optimized = {}
for key, val in random_series.items():
    for k in k_values:
        estimated_pdf = pdf_optimized(k, val[:N])
        theoretical_pdf = pdf_function[key](estimated_pdf['x'])
        metrics_optimized.setdefault(key, []).append(
            KL_dist(theoretical_pdf['y'], estimated_pdf['y']))

metrics_custom = {}
for key, val in random_series.items():
    for k in k_values:
        estimated_pdf = pdf_custom(k, val[:N])
        theoretical_pdf = pdf_function[key](estimated_pdf['x'])
        metrics_custom.setdefault(key, []).append(
            KL_dist(theoretical_pdf['y'], estimated_pdf['y']))

plt.figure(figsize=(12, 4))
plt.subplot(1, 2, 1)
for key, val in metrics_optimized.items():
    plt.scatter(k_values / N, val)
plt.legend(metrics_optimized.keys())
plt.xlabel('k / N')
plt.ylabel('KL-divergency')
plt.title('Метод на основе гистограмм')

plt.subplot(1, 2, 2)
for key, val in metrics_custom.items():
    plt.scatter(k_values / N, val)
plt.legend(metrics_custom.keys())
plt.xlabel('k / N')
plt.ylabel('KL-divergency')
plt.title('Метод на основе функции распределения')

В результате ожидаемо в обоих случаях получаются монотонно возрастающие зависимости метрики от соотношения (Рисунок 2), однако, метод, основанный на численном дифференцировании функции распределения случайной величины дает на порядок меньшее расхождение кривой оценки плотности распределения с теоретической кривой, чем метод, основанный на построении гистограммы, что особенно заметно при больших значениях .

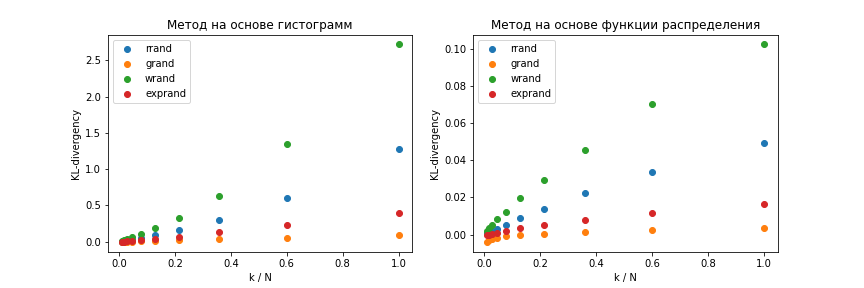
Заключение

Предложенный альтернативный метод построения оценок плотности распределения случайной величины по заданному набору наблюдений отличается более высокой точностью, по сравнению с методом, основанным на получении гистограмм. 

Выражаю благодарность MilashchenkoEA за обсуждение данных проблем и за то, что убедил написать эту небольшую заметку :)