Стресс-тестирование кредитного портфеля банка преследует цель сформировать ожидаемую оценку потерь в зависимости от прогнозных сценариев макроэкономических факторов. При этом базовой метрикой стресс-теста, как правило, выступает именно ожидаемые потери — математическое ожидание или, в случае с регрессией, условное по макрофакторам математическое ожидание потерь. Однако, если получается построить распределение таких потерь, то тогда стрессовые потери можно определять вероятностно, используя доверительные интервалы и метрики самого распределения.

Мы — команда портфельных моделей в ВТБ и сегодня расскажем об одном из подходов к стресс-тестированию банковского кредитного портфеля, который мы применяем у себя в банке.
Такой подход, безусловно, формулирует более комплексный взгляд на проблематику возможной динамики стоимости портфеля и позволяет в терминах вероятности оценить сценарные потери по моделируемому объекту.
Сложность задачи определяется прежде всего периметром моделирования и соответственно полнотой статистики, на основе которой формируются и рассчитываются целевые переменные, описывающие уровень потерь. В базовом варианте кредитный портфель может быть разделен на стандартный сегмент– самую массовую или «ликвидную» часть и некоторое множество отраслевых сегментов. Исходя из этого, объект моделирования может содержать либо достаточную или насыщенную историю дефолтов, которая позволит группировать заемщиков внутри сегмента для более точного прогноза потерь, либо статистики «хватит» для построения одной на весь сегмент целевой переменной, либо статистики будет недостаточно и тогда по такому сегменту необходимо будет искать некоторое прокси целевой переменной или же ориентироваться при моделировании на историю рейтинговых переходов заемщиков внутри сегмента.
Таким образом, все модели стресс-тестирования должны учитывать особенности сегментов кредитного портфеля как объектов моделирования, в первую очередь с точки зрения специфики их целевых переменных. Именно эта специфика, связанная с полнотой данных, и будет формировать некоторую каскадность в моделировании: там, где статистики достаточно, возможно использование симуляционных моделей с тонкой настройкой (использующих уровни дефолта(DR) для различных группировок заемщиков по рейтингам), по мере уменьшения данных для построения целевых переменных могут быть применены регрессионные модели прогнозирования, калибруемые на прокси целевых переменных, или же модель, использующая статистику рейтинговых переходов. Общий подход к моделированию потерь и применению моделей, учитывающих все описанные особенности и основные вводные задачи стресс-тестирования большого и разнородного кредитного портфеля (КП), будет показан ниже.
Целевые переменные
Формирование целевой переменной происходит по следующему принципу: в случае достаточной статистики дефолтов — разбиение рейтинговой шкалы на группы, в случае незначительного числа целевых событий на истории — без разбиения, иначе – с помощью прокси-переменной.
В процессе моделирования используются два типа целевых переменных:
DR
Proxy DR
DR (Default Rate) — рассчитывается на отчётную дату, как доля клиентов в рейтинговой группе относительно общего числа недефолтных клиентов, вышедших в течении года в дефолт, и не имеющих признаков дефолта на рассматриваемую дату оценки показателя. Рейтинговая группа в общем случае формируется из заемщиков моделируемого сегмента кредитного портфеля Банка, рейтинги которых относятся к одному подмножеству Мастер-Шкалы. В дальнейшем годовой DR может быть переведен в квартальную величину с использованием предположения о постоянстве частоты дефолтов по экспоненциальной формуле.
Proxy DR — рассчитывается аналогично DR, при условии использования вменённого числа дефолтов, получаемого путём умножения соответствующих величин Lifetime PD на число заёмщиков. Таким образом, прокси-переменная задаёт cредневзвешенную вероятность дефолта, где взвешивание ведётся по числу заёмщиков в каждом из рейтингов Мастер-Шкалы.
Используется следующая приоритизация построения моделей:
Разбиение Мастер-Шкалы на не менее, чем две рейтинговые группы, с последующей калибровкой регрессии Distance to default на макроэкономические факторы путём решением оптимизационной задачи, описываемой ниже;
DR для всей рейтинговой шкалы;
DR Proxy для всей рейтинговой шкалы;
Моделирование стрессовой матрицы миграций.
Модель отбора факторов
Одной из главных задач при построении модели стресс-тестирования потерь Стандартного сегмента КП (случай максимально полных статистических данных) является ее калибровка на историю дефолтов заемщиков с учетом портфельного эффекта посредством максимизации функции правдоподобия. При этом наборы значимых для того или иного разбиения (подмножеств) мастер-шкалы макрофакторов, которые участвуют в такой калибровке, определяются на отдельном этапе.
Концептуальной идеей модели отбора факторов является ранжирование длинного списка всех рассматриваемых показателей по значимости. Тогда, оперируя таким списком, можно предположить, что самым значимым будет первый фактор, лучшей комбинацией 2 факторов — первые 2 фактора, лучшей комбинацией 3 факторов — первые 3 фактора такого списка и так далее. При этом на финальном этапе модели отбора факторов каждая из таких комбинаций должна быть дополнительно проверена с учетом статистических тестов и кросс-валидации.
Прежде, чем факторы используются для применения в той или иной регрессионной модели, рассчитываются их оптимальные преобразования из определенного заранее набора вариантов (приращения, средние значения за разные периоды, лаги и т.д). При этом критерием оптимальности является максимизация корреляции с целевой переменной того или иного варианта преобразования фактора из всех рассматриваемых.
Для формирования списка отранжированных по значимости факторов используется ансамбль регрессионных моделей, в число которых входят: случайный лес; ridge регрессия, lasso регрессия, lasso-PCA регрессия, линейная регрессия, дерево решений и т.д.
Каждая модель калибруется на основе перебора всех ее гиперпараметров (Grid Search) и отдает на выходе набор скоринговых весов для каждого фактора. Вес фактора рассчитывается скалированием модулей коэффициентов перед факторами в случае обычных регрессий, либо, к примеру, значений features importance для леса. Итоговый скорринговый балл для фактора определяется обратно пропорциональным величине ошибки модели взвешиванием скорринговых весов по всему ансамблю моделей.
На полученные таким образом лучшие комбинации 1, 2, 3, 4 и т.д. факторов строится одна или несколько итоговых моделей прогноза целевой переменной для рассматриваемого подмножества рейтинговой шкалы, факторы проходят стандартные статистические тесты на значимость, оцениваются теоретические предпоссылки для остатков модели, проводится кросс-валидация. Таким образом, для каждой целевой переменной с учетом всех вышеприведенных критериев будет выбран один оптимальный набор макрофакторов.
Разбиение рейтинговой шкалы
Одной из основных идей модели стресс-тестирования сегмента Стандартный кредитного портфеля Банка является оптимальное разбиение рейтинговой шкалы для того, чтобы сформировать подмножества (то есть объединения подряд идущих рейтингов) однородных по уровню риска заемщиков. Такие подмножества должны формировать целевые переменные в виде уровней дефолтов, которые можно было бы максимально точно прогнозировать посредством доступного пула макрофакторов.
Глубина разбиения регулируется применением фильтра на долю нулевых значений целевой переменной. То есть отсекаются варианты подмножеств, где совокупное число дефолтов приводит к образованию доли нулей выше установленного порога. Таким образом, с учетом такого фильтра рассматриваются все уникальные варианты полного разбиения рейтинговой шкалы на непересекающиеся подмножества.
В конечном итоге для каждого подмножества, входящего в рассматриваемый вариант разбиения шкалы, применяется модель отбора факторов. Выбираются те варианты разбиений, для которых худшие значения метрик качества с учетом кросс-валидации моделей для одного из подмножеств, построенных на оптимальную комбинацию факторов, удовлетворяют установленным ограничениям снизу. При этом модель отбора факторов, как было описано ранее, для каждого подмножества на предыдущем этапе отобрала комбинации факторов с учетом ограничений по статистической значимости.
При этом в случае хорошей предсказательной способности пула макрофакторов могут быть отобраны несколько вариантов оптимальных разбиений шкалы. Тогда со стороны бизнес-подразделения банка возникает возможность выбрать такое разбиение, которое бы наилучшим образом отвечало бизнес логики с точки зрения состава макрофакторов, качества их сценариев, направлений зависимостей с целевой переменной итд.
Расчет distance-to-default и симуляция потерь
Для каждой рейтинговой группы и ее релевантных наборов факторов (при моделировании потерь сегмента Стандартный), определенных на этапе отбора факторов и поиска оптимального разбиения, в итоговом варианте задается следующее уравнение для уровня дефолтов группы (DD- distance-to-default):
Z – отобранные факторы, a – коэффиценты регрессии.
Тогда, учитывая портфельный эффект реализации событий дефолтов, условная по системному фактору (Y) вероятность возникновения n(i) дефолтов для m(i) заемщиков для функции вероятности биномиального распределения может быть записана как:
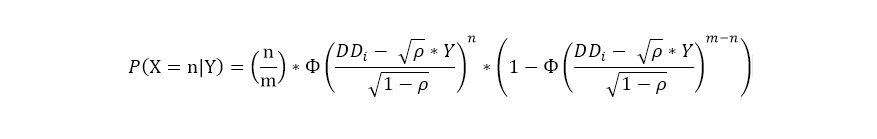
Если предположить, что Y~N(0,1), тогда маржинальную вероятность можно записать как:

С другой стороны интегральное выражение вида

можно аппроксимировать гауссово-эрмитовой квадратурой, то есть:
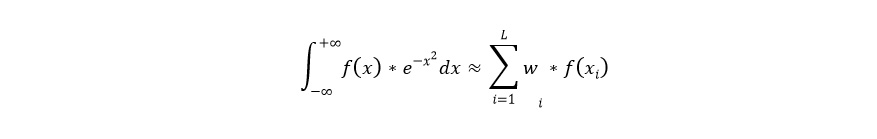
Где x(i) и w (i) cоответственно корни эрмитовых полиномов и их веса, а L- число используемых корней. Тогда выражение для маржинальной вероятности можно записать в следующем виде:
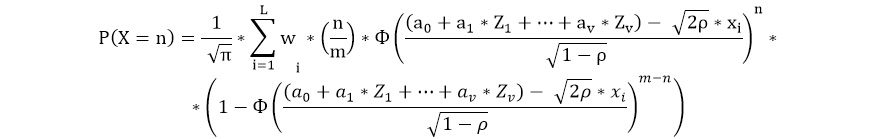
Коэффициенты регрессии и модельная корреляция находятся посредством поиска по их значениям глобального максимума функции правдоподобия:

Распределение потерь по портфелю рассчитывается численно методом Монте-Карло. Используя модель Васичека, симулируются стандартно нормально распределенные случайные величины, отвечающие за общий для заемщиков системный и индивидуальный для каждого заемщика в отдельности идиосинкратический риски. Сумма взвешенных по корреляции случайных величин сравнивается с прогнозным значением DD группы, к которой относится заемщик, определяя таким образом возникновение или невозникновение события дефолта по нему.
То или иное значение DD для прогнозного периода рассчитывается в зависимости от сценариев по макрофакторам, используя ранее откалиброванные регрессионные уравнения. После проведения описанной выше симуляционной процедуры для следующего шага моделирования заемщики мигрируют между рейтинговыми группами при помощи симуляции переходов по матрице групповой миграции и далее алгоритм повторяется снова.
Ансамбль регрессионных моделей для одной целевой переменной
Наибольшее количество информации для построения целевой переменной содержится безусловно в базовом– стандартном сегменте кредитного портфеля. Это позволяет фрагментированно группировать заемщиков для более точной симуляции потерь различных уровней риска. Следующими по «плотности» информации можно определить сегменты, которые невозможно разбить на рейтинговые подмножества при условии выполнения достаточных уровней качества моделей, описывающих соответствующие целевые переменные. А также сегменты, целевые переменные которых можно заменить на те или иные прокси.
В этом случае может быть применен подход, изложенный в пункте 3– модели отбора факторов. На заключительном этапе после того как список всех факторов получил скорринговые оценки и был отранжирован по значимости, на все лучшие комбинации первых 2, 3, 4 и т.д. факторов строится семейство моделей предсказания. Из них на основе тестов статистической значимости и результатов кросс-валидации выбирается лучшая.
Отношение прогноза отобранной модели, полученного по сценариям соответствующих факторов, делится на среднюю тенденцию целевой переменной. Данный коэффициент корректирует вероятность дефолта для данного сегмента и данного рейтинга заемщика при расчете ожидаемых потерь.
Регрессионная модель для матриц переходов
Для сегментов кредитного портфеля Банка, по которым статистика дефолтов крайне мала либо же вовсе отсутствует, может быть применена одна из моделей регрессии исторической матрицы переходов на макрофакторы для стресс-тестирования потерь. Например, вероятности перехода матрицы миграции в общем случае могут быть выражены следующим образом:

Для первого и последнего столбца матрицы вероятности представляются как:

Здесь F (*) - некоторая функция от рассматриваемых стрессовых факторов, например, такого вида:
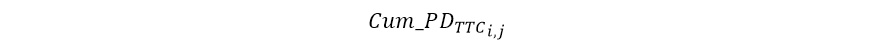
Квартальная TTC матрица переходов, на основе которой рассчитываются кумулятивные вероятности для i-го рейтинга, оценивается на всей истории разработки модели одним из классических методов.
Для того, чтобы откалибровать модель на истории необходимо сформировать на каждый временной срез матрицу реализованных переходов и по этой вспомогательной выборке оцениваются параметры (p, a) через поиск максимума функции:

М - количество рейтингов
n (i, j, t) - количество переходов из i в j на срез времени t
После того как параметры модели оценены, к исторической матрице переходов добавляется последний столбец, состоящий из вероятностей дефолтов для сегмента. Далее происходит соответствующая нормировка матрицы и после этого, зная параметры модели, возможно оценить все вероятности переходов и стрессовые вероятности дефолтов матрицы.
Используя стрессовые прогнозы значений макрофакторов, например, на поквартальной основе мы можем получить набор форвардных стрессовых квартальных матриц миграций, каждая из которых зависит от своих прогнозов. Перемножая все такие матрицы, мы получим стрессовую матрицу перехода на нужный нам период прогнозирования, при помощи которой не сложно рассчитать ожидаемые потери по сегменту.

