Привет, Хабр! Меня зовут Илья Котов, я Data Scientist в Сбере, участник профессионального сообщества NTA. Эта статья — первая часть небольшого цикла, посвящённого алгоритмам вложения вершин графа в векторное пространство. Сегодня расскажу об алгоритмах, основанных на матричных факторизациях. В качестве примера в статье используется занимательная задача поиска сообществ в графе. Что же, приступим!

Начнём с постановки задачи

Давайте представим, что в школе X учится старшеклассник, который создал собственную социальную сеть. Всю школу поразила его изобретательность, все пытаются стать пользователями его творения. На переменах (а иногда и на уроках) то и дело обсуждают его продукт плюс активно используют, непрерывно нажимая указательным пальцем на экран телефона.

Автор проекта понимает, что его пользовательская база стала достаточно большой, пользователи приходят уже из других школ, а школьники из кружков по программированию присылают свои резюме для участия в развитии социальной сети. Но успех не будет вечен, людей необходимо удерживать новым функционалом и возможностями.

Тогда голову старшеклассника посетила гениальная мысль: «А почему бы не сделать систему, которая будет рекомендовать вашему пользователю потенциального друга?» Но как это сделать?

На примере этой задачи я разберу алгоритмы вложений графов, основанные на матричном разложении, чтобы впоследствии вы смогли использовать эти алгоритмы и для своих прикладных задач. Приступим.

Разрабатываем алгоритм рекомендации «друзей» в социальной сети

 Нечто подобное вы могли видеть в vk.com.

Программисты из VK, безусловно, никогда не раскроют алгоритм рекомендации, но примерный принцип работы алгоритма понятен.

Вероятно, друг — это человек, с которым у вас есть что-то общее, возможно, хобби, работа, место учёбы, музыкальные предпочтения. Продолжать можно до бесконечности.

Как правило (но необязательно), вы знакомы с друзьями своего друга или даже с друзьями друга вашего друга. Также, скорее всего, у вас и вашего друга есть много общих друзей и знакомых. Соответственно, друзья и знакомые находятся примерно в общем социальном окружении, социальном кластере.

Зачем нам графы?

Теперь вернёмся к проекту нашего старшеклассника. В мире, полном сложных структур и закономерностей, ему нужен гибкий инструмент, который позволяет в достаточной мере хранить в себе информацию для последующего анализа. Графы — один из вариантов, который может решить эту задачу и помочь юному разработчику обрести ещё большую популярность.

Общество очень удобно моделировать с помощью графа, его приложение вы точно встретите в социологии. Давайте считать вершинами графа пользователей, а отношения между этими вершинами будут только в том случае, если (пользователь X *дружит* с пользователем Y). Отношения обладают свойством симметричности (для нашего случая), то есть это означает, что если (пользователь X *дружит* с пользователем Y), то и (пользователь Y *дружит* с пользователем X). Это в идеальном мире, а вот в реальной жизни такая система не всегда работает.

В качестве набора данных выступает граф дружбы выборки пользователей из социальной сети Facebook (данные были анонимизированы, источник — Stanford Large Network Dataset Collection).

Как анализировать эти графы? Хотелось бы применять привычные и всеми любимые алгоритмы машинного обучения, нейросети и статистику, но уже к данным, представленным в виде графа. На самом деле старшекласснику не нужно изобретать что-то новое, требуется лишь найти способ перейти из вершин и отношений в обычное векторное пространство, сохраняя при этом топологию графа. Эти векторы дадут возможность использовать инструменты, перечисленные выше, в том числе и алгоритмы кластеризации, для нахождения кластеров вершин, это и нужно старшекласснику.

Матрица смежности приходит на помощь

Матрица смежности — довольно простой, но мощный инструмент.

Формальное определение звучит так:

Матрица смежности графа G — квадратная матрица размера N × N,где N-количество вершин графа G, в которой значение элемента A(i,j) равно числу рёбер из i вершины графа в j-ую.

В самом простом случае неориентированного графа — это симметричная матрица, заполненная нулями и единицами. 

Старшеклассник выгрузил данные пользователей из соседних классов, и вот что у него получилось:

import networkx as nx
import matplotlib.pyplot as plt
%matplotlib inline
plt.figure(figsize=(10, 5))
graph = nx.Graph()
graph.add_edges_from(data)
plt.subplot(1, 2, 1)
nx.draw(graph)
plt.subplot(1, 2, 2)
plt.imshow(nx.adjacency_matrix(graph).toarray())

Жёлтый цвет означает единицу (то есть существует связь), тёмно-фиолетовый означает ноль (отсутствие связи).

Несложно заметить, что граф имеет 2 выраженные группы и 1 группу, которая их соединяет. В этом графе всё просто и наглядно, он является скорее примером для понимания, чем реальной задачей с неочевидной структурой.

Если вы посмотрите на строки этой матрицы как на векторы, то они уже могут характеризовать вершины графа.

Сингулярное разложение матрицы

SVD (Singular Value Decomposition) — крайне важный и красивый факт линейной алгебры. Это представление прямоугольной матрицы в виде произведения трёх матриц особого вида (обычно пишут U S V^t).

Чтобы разложить матрицу через SVD, вы можете использовать пакет из библиотеки numpy, называется он linalg.

import numpy as np

U, S, V_t = np.linalg.svd(X)

У сингулярного разложения есть наглядный геометрический смысл. Матрицы U и V (левые и правые сингулярные векторы) — унитарные матрицы (более общий случай ортогональных матриц, то есть они совершают повороты в пространстве или выворачивают его, в случае отрицательного детерминанта, сохраняя длину векторов), а S — это диагональная матрица, элементы на диагонали — сингулярные значения (то есть геометрически она совершает функцию масштабирования).

Теперь применим это к матрице смежности. Роль векторов вершин будут исполнять строки матрицы U. Так как сингулярные числа в диагональной матрице S идут по убыванию (то есть s1>s2.. > sn), можно отбросить последние столбцы матрицы U (если быть точнее, то последние сингулярные векторы матрицы U), потому что они имеют небольшой вклад в формирование матрицы, а места занимают много. Это в целом проблема для больших графов, где очень много вершин, а связей мало, матрица смежности становится разреженной. Такие графы лучше представлять в виде простого списка отношений. Сингулярное разложение матрицы тем и удобно, что даёт представление об общей структуре, помогает понять геометрический смысл, найти шумы и оставить только самые весомые признаки.

(значения на главной диагонали матрицы S)

Пусть r = 2, для того, чтобы была возможность визуализировать данные на плоскости.

На изображении видно, что часть информации утеряна, однако чётко выделяются 3 группы.

Вот как изменяется детализация матрицы смежности в зависимости от параметра r.  

plt.figure(figsize=(15, 5))

for i in range(1, 19):

            plt.subplot(2, 9, i)

            plt.title(‘r=’ + str(i))

            plt.imshow(U[:, :i] @ np.diag(S[:i]) @ V_t[:i, :])

Визуализируем векторы матрицы U(nx2).

Алгоритм готов!

Наконец, у старшеклассника есть всё необходимое, и он готов перевернуть индустрию.

Вот что нужно сделать:

1. Найти матрицу смежности.

2. Разложить её с помощью SVD и обрезать столбцы матрицы левых сингулярных векторов.

3. Применить какой-нибудь алгоритм кластеризации.

Граф имеет довольно непростую структуру (см. первую картинку), однако всё равно различимы некоторые группы. Из-за сложности данных из матрицы левых сингулярных векторов нужно брать гораздо больше столбцов, чем в простейшем случае с двумя классами (в этом примере возьмём 100), иначе теряется  очень много информации.

import networkx as nx

import numpy as np

from sklearn.manifold import TSNE

#создадим простой граф и заполним его данными

graph = nx.Graph()

graph.add_edges_from(relations) #relations — это список, где элементом является кортеж вида ('n1', 'n2')

#матрица смежности

adj_matrix = nx.adjacency_matrix(graph)

#svd разложение

u, sigma, v_t = np.linalg.svd(adj_matrix.toarray())

#обрежем матрицу левых сингулярных векторов до 100

large_vectors = u[:, :100]

#снизим размерность до двух компонент для визуализации

emb = TSNE(n_components=2).fit_transform(large_vectors)

Далее используем алгоритм DBSCAN для кластеризации. Кластер, в котором находится пользователь, — это его социальное окружение. Людей, которые входят в него и при этом не дружат (не имеют контактов в социальной сети) с нашим пользователем, я и буду предлагать в качестве возможного друга или знакомого. Система довольно простая, но вы можете её расширять, например, обращать внимание на интересы пользователя, на какие группы он подписан, какую музыку слушает, где живёт и так далее, делая систему всё более эффективной.

from sklearn.cluster import DBSCAN

import seaborn as sns

df_scatterplot = pd.DataFrame(emb, columns=['e1', 'e2'])

df_scatterplot['label'] = DBSCAN(eps=2, min_samples=2).fit(emb).labels_

plt.figure(figsize=(10, 10))

sns.scatterplot(data=df_scatterplot, x='e1', y='e2', hue='label', s=8, palette='deep')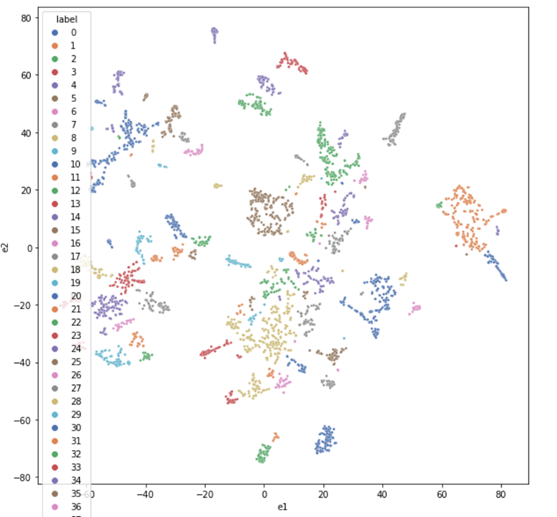

Собственно, на этом всё, конец первой части. Напомню, что сегодня я разобрал простой, но эффективный алгоритм, который может быть применён для ваших рабочих задач, где требуется анализ данных, представленных в виде графа. Алгоритмы, основанные на матричных факторизациях, обобщаются и на мультиграфы, только речь будет идти уже о тензорной факторизации (см. DistMult и т. п.). В следующей части я рассмотрю не менее интересные алгоритмы, основанные на случайных блужданиях.

Если у вас во время прочтения статьи возникли вопросы, задавайте их в комментариях, постараюсь ответить на все. А если вы работаете с алгоритмами рекомендаций и у вас есть предложения, пишите, обсудим.