В своей последней статье я попытался создать фрактал, порожденный простыми числами. Но он меня не очень устроил эстетически. Поэтому я решил воспользоваться zeta функцией Римана для создания фракталов.

Самый популярный фрактал, фрактал Мандельброта, создается итерацией функции:

где X - комплексное число, а с - значение, которое для каждого пикселя берется согласно позиции этого пикселя. Если итерация уходит в бесконечность, то мы рисуем цвет согласно числу итераций до того, как функция превысила некоторое значение, а если такого не происходит, то мы рисуем пиксель черным. В качестве начального значения. X0. используется 0

Таким образом, при расчете фрактала Мандельброта для каждого пикселя используется разная функция. В отличие от такого подхода я в итерациях использовал одну и ту же функцию, от пикселя зависело только начальное значение, X0.

Первый эксперимент был с формулой

Особенно интересно поведение итераций вблизи нетривиальных корней, например первого (real = 0.5, img = 14.13..):

Желтая стрелка показывает, где находится первый корень. Цвета соответствуют числу итераций до abs(Z)>100. Сделаем zoom:

И еще:

И еще, мы сдвинулись вбок и корень уже ушел из поля зрения:

Мне кажется, этот фрактал можно назвать "бабочки Римана"?

Лирическое отступление о Julia

Я продолжал эксперименты с другими формулами, но процесс генерации миллиона точек (1000x1000) на Python занимал иногда до одного дня. Дело не только в медленности самого Python - подходящий пакет с zeta я нашел только в mpmath - вычисления с произвольной точностью. Это замечательный пакет, но очень медленный.

Я решил перескочить на другой язык, и мое внимание привлек язык Julia. Быстрый и полностью компилируемый, он позволяет вольготно обращаться с типами, почти как Python. Кроме того, он очень хорошо организует multi-threading. Например, перед циклом расчета фрактала, где все точки вычисляются независимо, достаточно написать

Threads.@threads for j in 0:iry
  for i in 0:irx
    ...

и все. Вот она, кнопка "сделать все зашибись". (да, да, не все так просто). В итоге то, что на Python занимало день, считалось несколько секунд. Я вышел на новый уровень и вот некоторые новые вычисления снова уперлись в продолжительность ожидания)

Я перебрал очень много вариантов, некоторые не давали интересных фракталов, зато итерация точки создавала интересные аттракторы:

Нетривиальные нули zeta

Мне все же хотелось найти функцию, которая бы показала все нетривиальные корни - ведь в этом случае картинка содержит бесконечно тонкую структуру всех простых чисел вообще. Такой функцией оказалась

Сам по себе фрактал не был очень красивым, но у одного из его элементов была такая картина:

Как вы видите, расстояние между ножками соответствует расстоянию между корнями. Если увеличить острие хвостика второго корня:

то мы увидим ту же картину в более мелком масштабе.

Видео!

Но самой красивой оказалась формула

(условие выхода: Re(Xn)<-1.0)

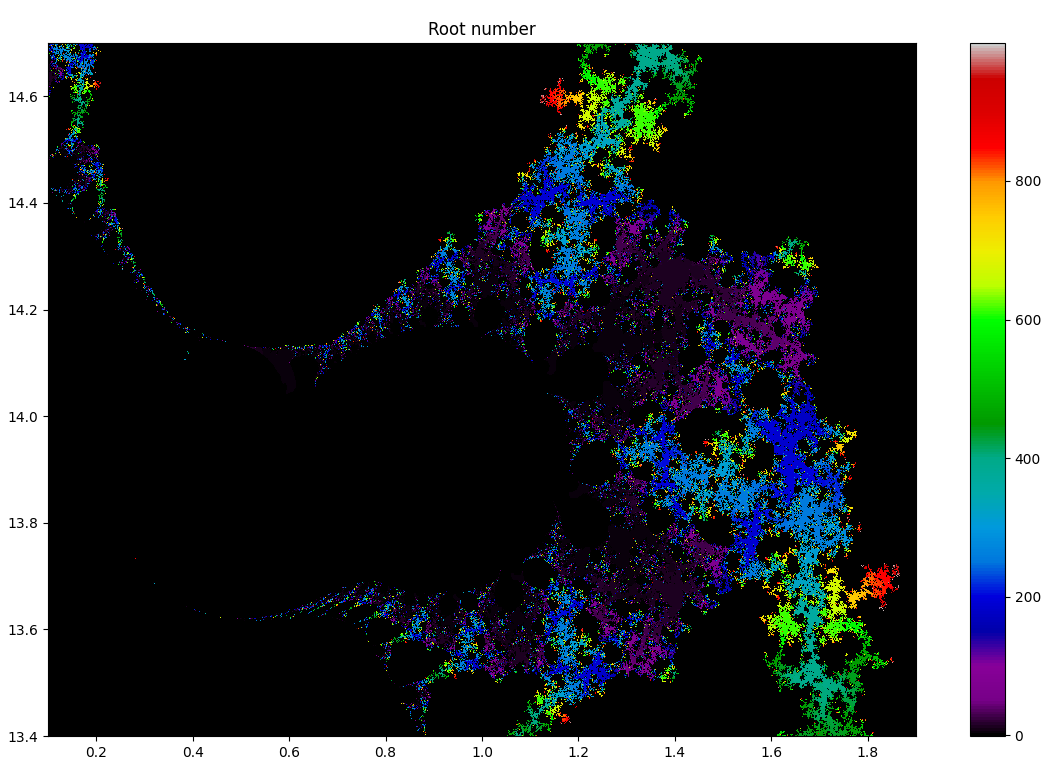
Цвета соответствуют ближайшему номеру корня, у которого остановился расчет.

Сделаем zoom:

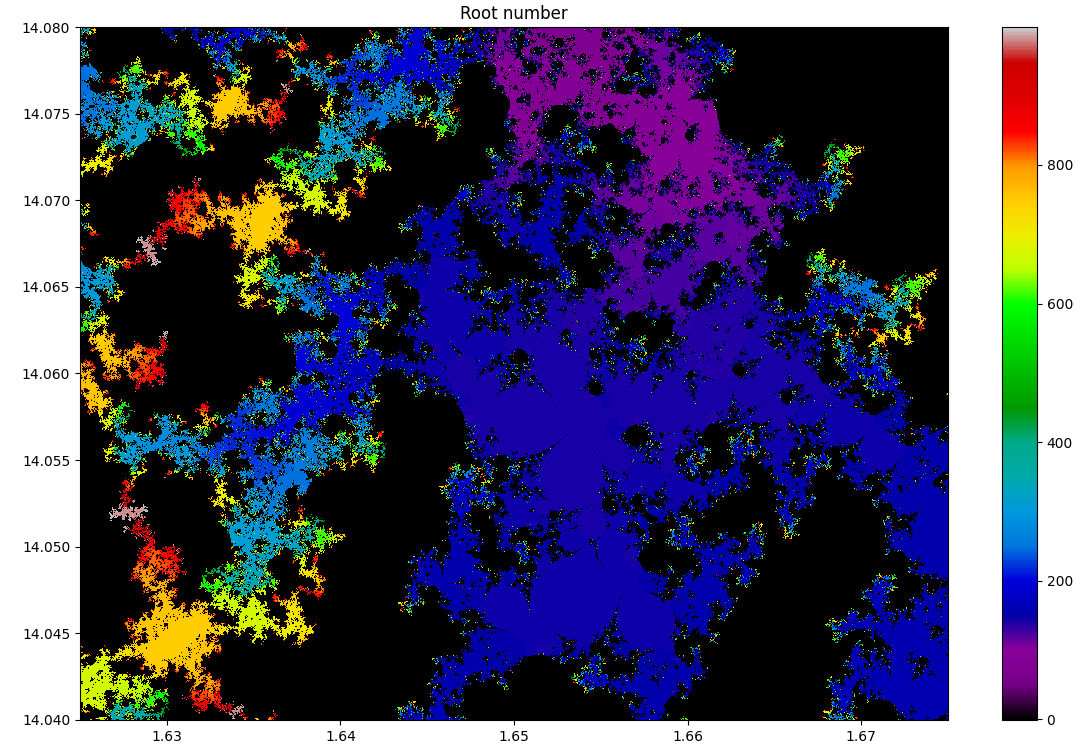
Можно заметить, что дерево 'растет' за счет все бОльших и бОльших корней. Это можно показать на видео: