В прошлый раз мы рассмотрели использование рекурсии на примере возведения в степень. В этот раз мы применим рекурсию для создания алгоритма сортировки слиянием.

В сети легко найти множество вариаций решения данной задачи. Код, который мы рассмотрим в этой статье, будет написан так, чтобы быть максимально простым для понимания начинающих разработчиков.

Освежим в памяти суть сортировки слиянием:

Изначальный массив делится пополам до тех пор, пока длина "половинок" не станет равна 1. Это - базовый случай. Затем элементы двух "половинок" сравниваются и заносятся в результирующий массив в порядке возрастания.

Поскольку мы сначала делим массив, а затем собираем обратно, удобнее будет вынести эти операции в отдельные методы. Будем последовательны и начнем с деления. Раз мы хотим делить массив пополам до тех пор, пока длина "половинок" на станет равна 1, будет удобно использовать рекурсию.

Вначале опишем базовый случай:

public static int[] mergeSort(int[] src) {
        if (src.length <= 1) return src;
    }

Затем "поделим исходный массив пополам". Это значит, что нам нужно создать два новых массива. Каждый возьмет половину элементов из исходного (src). Для простоты назовем их left и right. Применим метод Arrays.copyOfRange, в котором укажем по порядку:

1. Массив-источник, откуда будем копировать значения (src)

2. Индекс источника, с которого начнем (0)

3. Индекс источника, по достижению которого копирование прекратится* (src.length / 2)

int[] left = Arrays.copyOfRange(src, 0, src.length / 2);

* Размер left будет равен промежутку от индекса 0 включительно до индекса src.length / 2 исключительно.

Аналогично поступим для right. В качестве первого индекса для копирования возьмем тот, на котором остановилось копирование в массив left, (по сути, это будет его длина), и пройдем до конца массива-источника:

int[] right = Arrays.copyOfRange(src, left.length, src.length);

В итоге получим код:

public static int[] mergeSort(int[] src) {
        if (src.length <= 1) return src;
        int[] left = Arrays.copyOfRange(src, 0, src.length / 2);
        int[] right = Arrays.copyOfRange(src, left.length, src.length);
  }

Осталось применить рекурсию - и метод будет "делить пополам" до тех пор, пока размер массива не станет равен 1.

Но перед этим давайте напишем второй метод, в котором мы опишем логику слияния. Суть его работы будет заключаться в том, что мы создадим новый массив result, в который будем помещать элементы массивов left и right по возрастанию. Помимо массива result, нам потребуется объявить переменные, которые выступят в роли счетчика для индекса каждого из массивов:

private static int[] merge(int[] left, int[] right) {
  
        int[] result = new int[left.length + right.length];
  
        int resIn = 0, leftIn = 0, rightIn = 0;

Важно понять: поскольку мы начинаем объединение только после достижения базового случая (когда размеры массивов left и right равны 1), изначально мы сравниваем, по сути, просто два числа. Записывая их в порядке возрастания в результирующий массив размером 2, мы получаем маленький, но уже отсортированный массив. Логично, что нам достаточно написать код, который объединяет по возрастанию элементы именно отсортированных массивов. Нам не требуется сравнивать каждый элемент с каждым! Вот почему сортировка слиянием О(n*log₂(n)) быстрее сортировки путем сравнения каждого с каждым О(nⁿ).

Итак, нам достаточно сравнить первые элементы двух массивов. Меньший будет добавлен в результирующий массив. Больший - пойдет на сравнение со следующим элементом соседа:

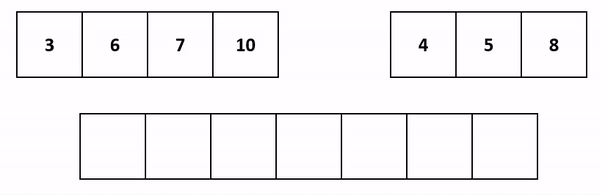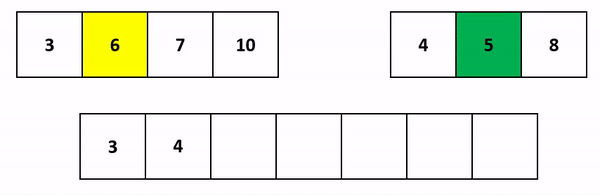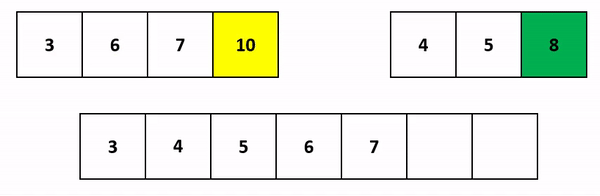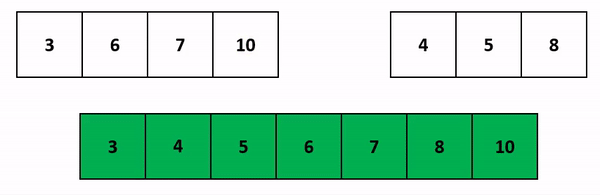
Напишем код. Поскольку массивы left и right могут быть разного размера, мы будем записывать значения в result, пока не дойдем до конца хотя бы одного из них:

while (leftIn < left.length && rightIn < right.length)
            if (left[leftIn] < right[rightIn]) 
              result[resIn++] = left[leftIn++];
            else result[resIn++] = right[rightIn++];

Если в цикле выше мы дошли до конца одного массива, но не дошли до конца второго, то оставшиеся элементы также потребуется добавить к результирующему массиву:

while (resIn < result.length)
            if (leftIn != left.length) 
              result[resIn++] = left[leftIn++];
            else result[resIn++] = right[rightIn++];

Осталось только вернуть result. Код метода целиком:

private static int[] merge(int[] left, int[] right) {

        int[] result = new int[left.length + right.length];

        int resIn = 0, leftIn = 0, rightIn = 0;
       
        while (leftIn < left.length && rightIn < right.length)
            if (left[leftIn] < right[rightIn]) 
                result[resIn++] = left[leftIn++];
            else result[resIn++] = right[rightIn++];
        
        while (resIn < result.length)
            if (leftIn != left.length) 
                result[resIn++] = left[leftIn++];
            else result[resIn++] = right[rightIn++];

        return result;
    }

Итак, наши методы готовы. Остался последний штрих - добавление рекурсии:

public static int[] mergeSort(int[] src) {
        if (src.length <= 1) return src;
        int[] left = Arrays.copyOfRange(src, 0, src.length / 2);
        int[] right = Arrays.copyOfRange(src, left.length, src.length);
  
        return merge(mergeSort(left), mergeSort(right));
    }

Теперь метод mergeSort, который делит массив на две половины, сам будет запрашивать результат их слияния. А слияние начнется только после того, как left и right достигнут базового случая, так как мы обращаемся к ним через тот же самый mergeSort. И вот, когда базовый случай достигнут, метод merge начнет сборку, а метод mergeSort - отправлять результат в merge, который был вызван предшествующей итерацией. В конце концов, мы дойдем до самого начала рекурсии и получим ответ.

Весь код целиком:

public static int[] mergeSort(int[] src) {
        if (src.length <= 1) return src;
        int[] left = Arrays.copyOfRange(src, 0, src.length / 2);
        int[] right = Arrays.copyOfRange(src, left.length, src.length);
        return merge(mergeSort(left), mergeSort(right));
    }

private static int[] merge(int[] left, int[] right) {
        int resIn = 0, leftIn = 0, rightIn = 0;
        int[] result = new int[left.length + right.length];

        while (leftIn < left.length && rightIn < right.length)
            if (left[leftIn] < right[rightIn])
                result[resIn++] = left[leftIn++];
            else result[resIn++] = right[rightIn++];

        while (resIn < result.length)
            if (leftIn != left.length)
                result[resIn++] = left[leftIn++];
            else result[resIn++] = right[rightIn++];

        return result;
    }

Бонус: метод merge можно записать в короткой форме, чуть более сложной для восприятия:

private static int[] merge(int[] left, int[] right) {
        int[] result = new int[left.length + right.length];
        for (int k = 0, i = 0, j = 0; k < result.length; k++)
            result[k] = i < left.length && (j == right.length || left[i] < right[j]) ? left[i++] : right[j++];
        return result;
    }