Много внимания в последнее время уделяют крупным нейронным сетям с миллиардами параметров, и это не случайно. Комбинируя множество параметров с мощными архитектурами, такими как трансформеры и диффузия, нейросети способны достичь удивительных высот. Под катом — к старту нашего флагманского курса по Data Science — разберём, как именно работает маленькая нейросеть-сумматор. Возможно, это удивит вас.

Но даже небольшие сети могут быть на удивление эффективными. Особенно если их разработали под конкретные задачи. В одной из частей своей прошлой работы я обучал небольшие (< 1000 параметров) сети отображению последовательности в последовательность и решению других простых логических задач. Ради небольших интерактивных визуализаций их внутренних состояний я хотел сделать модели как можно меньше и проще.

После решения очень простых задач я попытался обучить нейронные сети двоичному сложению. Сети получали на вход биты для двух 8-битных целых чисел без знака (они преобразовывали биты во float в виде «-1» для двоичного «0» и «+1» — для двоичной «1») и должны были производить правильное сложение, включая перенос переполнений [речь идёт о разрядах "в уме"].

Пример обучения в виде двоичного кода:

01001011 + 11010110 -> 00100001

Векторы входных и выходных данных для нейросети:

вход: [-1, 1, -1, -1, 1, -1, 1, 1, 1, 1, -1, 1, -1, 1, 1, -1]
выход: [-1, -1, 1, -1, -1, -1, -1, 1]

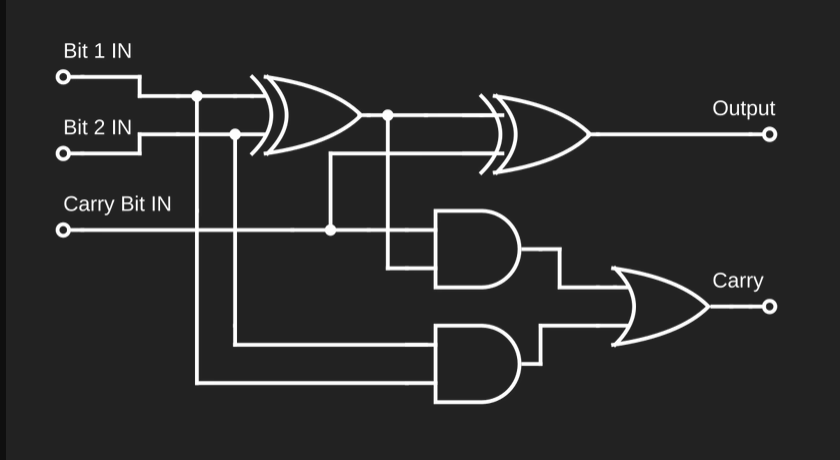
Я надеялся, что сеть будет изучать данные внутри себя по аналогии со схемой двоичного сумматора (по крайней мере я так это себе представлял):

Принципиальная схема полного сумматора для одного бита. Она показывает три входных бита для двух складываемых битов, бит переноса и два выходных бита для вывода сложения, и бит переноса. Пять различных логических вентилей, включая XOR, AND и OR, соединены со входами, выходами и друг с другом линиями для обозначения потока данных в схеме.

Я ожидал, что такая схема определит взаимосвязи между разными битами на входе и выходе, направит их по необходимости, а нейроны использует как логические вентили. Подобное я видел в других задачах, которые довелось потестить.

Обучение сети

Для начала я создал сеть с довольно обширной архитектурой. Она имела 5 слоёв и несколько тысяч параметров. Однако я не был уверен, что даже этого будет достаточно. Приведённая выше логическая схема двоичного сумматора обрабатывает только один бит; для добавления 8 бит к 8 битам потребуется гораздо большее количество логических вентилей, и сеть должна будет моделировать их все.

Я не был уверен и в том, как сеть будет обрабатывать длинные цепочки переносов. Например, при сложении 111111111111 + 00000001 она зацикливается (wraps), а на выходе получается 000000. Чтобы такое произошло, перенос из наименьшего значащего бита должен распространиться через весь сумматор в самый старший значащий бит. Я подумал, что, скорее всего, чтобы вести себя так, сети нужно не меньше восьми слоёв.

И снова я не был уверен, что сеть вообще сможет чему-то научиться, но приступил к её обучению.

Обучающие данные я создал путём генерации случайных 8-битных беззнаковых, складывая их с зацикливанием. Чтобы получить представление о том, насколько хорошо работает сеть в целом, к тем потерям, которые вычисляются во время обучения, я добавил код периодической проверки точности сети для всех 32 385 возможных комбинаций входных данных, возникающих во время обучения.

После кое-какой настройки гиперпараметров вроде скорости обучения и размера пакета я с удивлением обнаружил, что модель обучается очень хорошо! Я смог довести её до того, что она сходилась к идеальным или близким к идеалу решениям почти при каждом прогоне обучения.

Скриншот графиков потерь и точности валидации модели во время обучения. Потери обозначены как MSE — среднеквадратичная ошибка. Точность валидации указана в процентах. Потери со временем снижаются с ~1 до 0,01, а точность валидации повышается с 0% ровно до 100%.

Я хотел знать, как работает сеть изнутри, когда генерирует решения. Сети, которые я обучал, были чрезмерно параметризированы для поставленной задачи. Понять, что они делают, было очень сложно: для этого было нужно продраться сквозь десятки тысяч весов и смещений. Поэтому я начал урезать сеть — удалять слои и уменьшать количество нейронов в каждом слое.

К моему застывшему изумлению, сеть продолжала работать! В какой-то момент идеальные решения стали встречаться реже, поскольку сеть стала зависеть от удачи в установке начальных параметров, но я смог заставить её выучить идеальные решения всего с 3 слоями и числом нейронов 12, 10 и 8 соответственно:

Слой (тип)           Входная размерность    Выходная размерность  Параметры #
===========================================================
input1 (InputLayer)    [[null,16]]    [null,16]     0
___________________________________________________________
dense_Dense1 (Dense)   [[null,16]]    [null,12]     204
___________________________________________________________
dense_Dense2 (Dense)   [[null,12]]    [null,10]     130
___________________________________________________________
dense_Dense3 (Dense)   [[null,10]]    [null,8]      88
===========================================================

Всего 422 параметра! Не ожидал, что сеть сможет обучиться такой сложной функции при столь небольшом числе параметров.

Честно говоря, мне казалось, что всё это слишком хорошо, чтобы быть правдой, и хотелось убедиться, что я не совершил никаких ошибок при обучении сети или проверке результатов. Обзор кода генерации примеров и конвейера обучения не выявил ничего предосудительного. Дальше нужно было посмотреть параметры после успешного прогона обучения.

Уникальные функции активации

На этом этапе важно отметить функции активации, используемые для разных слоев модели. Часть моей предыдущей работы в этой области состояла в разработке и реализации новой функции активации для нейронных сетей, чтобы реализовать двоичную логику как можно эффективнее. Среди прочего, эта функция способна моделировать любую двухвходовую булеву функцию в одном нейроне, то есть она решает проблему исключающего или (XOR).

Подробнее об этом — в другой моей статье, здесь же я просто оставлю ссылку.

Он выглядит как один период уплощённой синусоиды и имеет несколько управляемых параметров для регулировки плоскостности и обработки входных параметров за пределами диапазона.

Все модели, которые я обучал двоичному сложению, использовали эту функцию активации, которую я назвал Ameo, в первом слое. Для всех остальных слое они использовали tanh.

Разбор модели

Хотя число параметров теперь стало вполне управляемым, глядя на них, я всё ещё не мог понять, что происходит. При этом, как я заметил, многие параметры были очень близки к круглым значениям: 0, 1, 0,5, -0,25 и т. д.

Многие логические вентили, которые я моделировал ранее, получили такие параметры, поэтому я решил, что при поиске сигнала в шуме стоит уделить им внимание.

Я добавил небольшое округление и ограничение (clamping), которое применялось ко всем параметрам сети ближе некоторого порога относительно этих круглых значений. Округление и ограничение я применял периодически на протяжении всего обучения, давая оптимизатору некоторое время, чтобы приспособиться к изменениям в промежутках. После нескольких повторов и ожиданий, пока сеть снова сходится к идеальному решению, начали проявляться чёткие закономерности:

layer 0 weights:
[[0         , 0         , 0.1942478 , 0.3666477, -0.0273195, 1         , 0.4076445 , 0.25     , 0.125    , -0.0775111, 0         , 0.0610434],
 [0         , 0         , 0.3904364 , 0.7304437, -0.0552268, -0.0209046, 0.8210054 , 0.5      , 0.25     , -0.1582894, -0.0270081, 0.125    ],
 [0         , 0         , 0.7264696 , 1.4563066, -0.1063093, -0.2293   , 1.6488117 , 1        , 0.4655252, -0.3091895, -0.051915 , 0.25     ],
 [0.0195805 , -0.1917275, 0.0501585 , 0.0484147, -0.25     , 0.1403822 , -0.0459261, 1.0557909, -1       , -0.5      , -0.125    , 0.5      ],
 [-0.1013674, -0.125    , 0         , 0        , -0.4704586, 0         , 0         , 0        , 0        , -1        , -0.25     , -1       ],
 [-0.25     , -0.25     , 0         , 0        , -1        , 0         , 0         , 0        , 0        , 0.2798074 , -0.5      , 0        ],
 [-0.5      , -0.5226266, 0         , 0        , 0         , 0         , 0         , 0        , 0        , 0.5       , -1        , 0        ],
 [1         , -0.9827325, 0         , 0        , 0         , 0         , 0         , 0        , 0        , -1        , 0         , 0        ],
 [0         , 0         , 0.1848682 , 0.3591821, -0.026541 , -1.0401837, 0.4050815 , 0.25     , 0.125    , -0.0777296, 0         , 0.0616584],
 [0         , 0         , 0.3899804 , 0.7313382, -0.0548765, -0.021433 , 0.8209481 , 0.5      , 0.25     , -0.156925 , -0.0267142, 0.125    ],
 [0         , 0         , 0.7257989 , 1.4584024, -0.1054092, -0.2270812, 1.6465081 , 1        , 0.4654536, -0.3099159, -0.0511372, 0.25     ],
 [-0.125    , 0.069297  , -0.0477796, 0.0764982, -0.2324274, -0.1522287, -0.0539475, -1       , 1        , -0.5      , -0.125    , 0.5      ],
 [-0.1006763, -0.125    , 0         , 0        , -0.4704363, 0         , 0         , 0        , 0        , -1        , -0.25     , 1        ],
 [-0.25     , -0.25     , 0         , 0        , -1        , 0         , 0         , 0        , 0        , 0.2754751 , -0.5      , 0        ],
 [-0.5      , -0.520548 , 0         , 0        , 0         , 0         , 0         , 0        , 0        , 0.5       , 1         , 0        ],
 [-1        , -1        , 0         , 0        , 0         , 0         , 0         , 0        , 0        , -1        , 0         , 0        ]]

layer 0 biases:
[0          , 0         , -0.1824367,-0.3596431, 0.0269886 , 1.0454538 , -0.4033574, -0.25    , -0.125   , 0.0803178 , 0         , -0.0613749]

Выше приведены окончательные веса первого слоя сети после привязки и округления. Каждый столбец представляет параметры одного нейрона: первые 8 весов сверху вниз применяются к битам первого входного числа, а следующие 8 — к битам второго.

Все эти нейроны оказались в очень сходном состоянии. Есть закономерность удвоения весов по мере продвижения вниз по линии и совпадения весов между соответствующими битами обоих входов. Смещение выбрано так, чтобы оно соответствовало наименьшему по значимости весу. У разных нейронов — разные основания для множителей и разные смещения для стартового разряда.

Искусное решение сети

Поразмыслив над этим какое-то время, я начал понимать, как работает это решение.

Цифро-аналоговые преобразователи (ЦАП) — электронные схемы, которые принимают цифровые сигналы, разделённые на несколько входных битов, и преобразуют их в единый, аналоговый выходной сигнал.

ЦАП используются в таких приложениях, как воспроизведение аудио, где звуковые файлы хранятся в памяти в виде чисел. ЦАП принимают эти двоичные значения и преобразуют их в аналоговый сигнал, который используется для питания динамиков, определения их положения и создания вибрации воздуха, то есть звука. Например, в Nintendo Game Boy на каждом из двух выходных аудиоканалов встроили по одному 4-битному ЦАП.

Вот пример принципиальной схемы ЦАП:

Принципиальная схема ЦАП с 8 разными входами, по одному на бит. К ним подключены резисторы, сопротивления которых дублируются с каждым новым входом. У схемы единый выход, который представляет аналоговую версию выходных цифровых сигналов.

Если посмотреть на сопротивления резисторов, подключённых к каждому из битов двоичного входа, можно увидеть, что они удваиваются от одного входа к другому, начиная с наименее значимого бита и заканчивая наиболее значимым. Очень похоже на то, что сеть научилась делать с весами входного слоя. Основное отличие заключается в том, что там веса дублируются между двумя 8-битными входами.

Это позволяет сети как суммировать входные данные, так и преобразовывать сумму в аналоговый сигнал в пределах одного слоя/нейрона, причем всё это происходит ещё до того, как в игру вступают функции активации.

Но это лишь часть головоломки. Как только цифровые входные сигналы преобразованы в аналоговые и суммированы, они сразу же проходят функцию активации нейрона. Чтобы проследить, что происходит дальше, я построил график постактивационных выходов нескольких нейронов первого слоя по мере увеличения входных сигналов:

Ссылка на график

Казалось, что нейроны генерируют выходные сигналы синусоидального вида, которые с увеличением суммы двоичных входных сигналов плавно меняются. Периоды разных нейронов различны. У тех, что изображены выше, периоды равны 8, 4 и 32 соответственно. Другие нейроны имели другие периоды или смещение на определённые расстояния.

В этом графике есть кое-что интересное. Он точно повторяет периоды, где при двоичном счёте различные двоичные цифры переключаются между 0 и 1. Наименьшая значащая цифра переключается между 0 и 1 с периодом 1, вторая — с периодом 2, до 4, 8, 16, 32 и так далее. Это означает, что по крайней мере для некоторых выходных битов сеть научилась вычислять всё необходимое в одном нейроне.

Взгляд на веса нейронов в двух последующих слоях подтверждает это. Последующие слои в основном занимаются маршрутизацией выходов первого слоя и их комбинированием. Одно из дополнительных преимуществ этих слоев — «насыщение» сигналов и придание им более «квадратной» формы волны, то есть приближение их к целевым -1 и 1 для всех значений. Точно такое же свойство используется при цифровой обработке сигналов для синтеза звука. При этом tanh применяется, чтобы добавить в звук искажения для чего-нибудь типа гитарных педалей.

Играя с этой настройкой, я попробовал переобучить сеть, заменив функцию активации для первого слоя на sin(x), и в итоге она работает практически так же. Интересно, что в этом случае веса запоминаются при обучении в виде дробей не от 1, а от числа π.

Чтобы генерировать нужные ей выходные сигналы, с другими цифрами на выходе сеть научилась делать очень хитрые вещи. Например, объединила выходы первого слоя так, что создала версию сигнала со сдвигом, которой нет в любом из нейронов первого слоя, путём сложения сигналов других нейронов с разными периодами. Сработало довольно хорошо, и для целей сети этого более чем достаточно.

Версия функции на основе синуса, изученная сетью (синий цвет), в итоге оказалась примерно эквивалентна функции sin(1/2x + pi) (оранжевый цвет):

Скриншот графического калькулятора Desmos, где сравниваются графики функции sin(1/2x + pi) и функции -sin(1/2x) + sin(1/4x) - sin(1/6x), которая была изучена сетью. Они довольно близки и имеют максимумы и минимумы почти в одних и тех же точках.

Я понятия не имею, что это такое: очередная ли математическая случайность, часть какого-нибудь бесконечного ряда или что-то ещё. Так или иначе, получилось очень изящно.

Резюме

Таким образом, в целом сеть выполняла двоичное сложение через:

1. Преобразование двоичных входных сигналов в «аналоговые» при помощи версии цифро-аналогового преобразователя с использованием весов входного слоя.
2. Преобразование внутреннего аналогового сигнала в периодические синусоидальные сигналы с помощью функции активации Ameo, даже если она не периодическая.
3. Насыщение синусоидального сигнала, которое делает его более похожим на квадратную волну, приближает выходные сигналы для всех выходов к ожидаемым значениям, то есть к -1 и 1.

Как уже писал, я представлял себе, что для сложения в цифровом виде сеть обучается причудливо комбинировать логические вентили по аналогии с работой двоичного сумматора. Эта хитрость — ещё один пример того, как нейросети находят неожиданные решения.

Эпилог

После этого исследования мне пришло в голову, что огромные современные модели с миллиардами параметров можно построить с использованием на порядки меньших сетевых ресурсов за счёт применения более эффективных или специализированных архитектур.

Это, конечно, захватывает, но я сразу умерил свой пыл, когда вспомнил статью The Bitter Lesson. Если вы ещё не читали эту статью, прочтите её сейчас, она очень короткая. Эта статья действительно изменила мой взгляд на вычисления и программирование.

Даже если конкретно это решение было просто случайностью из-за архитектуры моей сети или моделируемой системы, после него я ещё более впечатлился мощью и универсальностью градиентного спуска и подобных ему алгоритмов оптимизации. По-настоящему поражает, что столь специфические схемы способны последовательно возникать из чистой случайности.

Я планирую продолжить работу с небольшими нейросетями и в итоге создать те визуализации, о которых говорил. Если вам интересно, подписывайтесь на мой блог по RSS в верхней части страницы и следите за обновлениями в Twitter @ameobea10 или Mastodon @ameo@mastodon.ameo.dev.

Ещё больше практики и полезной теории — на наших курсах:

• Профессия Data Scientist (24 месяца)
• Профессия Fullstack-разработчик на Python (16 месяцев)