14.02.2023 02:35
Omazz 21 5500 Источник

Disclaimer: данная статья подойдёт, на мой взгляд, прежде всего для новичков, которые ничего не понимают в фильтрации, а стандартный и адаптивный фильтры Калмана вызывают недоумение. Прошу отнестись к ней с этой оговоркой.
Фильтрация нужна везде, где есть шум, а значит её применение имеет очень широкий диапазон. Основными сферами использования являются инженерия и экономика.
Таким образом, далее при фильтрации будет идти речь о величине, которая нас интересует. Это может скорость, координата, угол -- всё что угодно.

Введение

Очень часто получаемая нами информация может не соответствовать действительности, из-за чего её использование в чистом виде может быть некорректно. Такое несоответствие как правило вызвано теми или иными шумами, но чаще всего при моделировании за шум принимают АБГШ (аддитивный белый гауссовский шум), имеющий относительно стабильную амплитуду. Фильтрация позволяет решить эту проблему.

Однако, фильтров существует огромное множество. Несмотря на их безграничное разнообразие, стандартом определённо является фильтр Калмана. К сожалению, человеку, который никогда с ним работал, может быть достаточно затруднительно определиться с его реализацией -- как минимум из-за выбора входных матриц.

Именно поэтому на начальных порах можно пренебречь некоторыми моментами и упростить фильтр Калмана до уровня α-β фильтра. Если же у читателя нет ни времени, ни желания на своё продвижение в этой теме, то рекомендуется пропустить следующую главу и перейти сразу к α-β фильтру.

Фильтр Калмана

Про фильтр Калмана можно писать очень много и очень долго, но я попробую описать всё тезисно. При этом, главная цель этого раздела -- показать, что сходу залезть в эту тему не так-то уж и просто, а вот реализовать α-β фильтр куда легче.

Итак, приступим. Пусть динамическая система описывается следующими линейными уравнениями:

z_k=Hx_k+v_k,

z_k -вектор\ измерения\ системы\ на\ шаге\ k

H - матрица\ перехода\ измерения

v_k -вектор\ шума\ измерения\ на\ шаге\ k

Тогда состояние объекта будем оценивать следующим образом:

x_{k+1}=Fx_k+w_k,

x_k -вектор\ системы\ системы\ на\ шаге\ k

F - матрица\ перехода\ состояния

w_k -вектор\ шума\ процесса\ на\ шаге\ k

При этом, шумы v_kи w_kимеют ковариационные матрицы Q_kи R_k соответственно. При этом, истинные значения этих матриц нам неизвестны, то есть нам нужно будет их оценивать самостоятельно.

Если Вам знакомо слово "ковариационные", а Ваши математические познания хоть сколько-то в порядке, то этот фильтр вполне реально осилить, прочитав другие статьи на этом прекрасном сайте, либо же прочитав соответствующую литературу. Фильтр Калмана можно изучать очень-очень долго, по-скольку там тоже есть свои нюансы, а можно остановиться на чём-то достигнутом -- мы будем довольствоваться самым тривиальным, но тем не менее достаточно действенным.

α-β фильтр Калмана

А оно нам вообще надо?

Конечно надо! Шумы есть практически в любой системе -- это могут быть как погрешности измерительных приборов, так и случайные ускорения, которые есть практически в каждой системе. Если же мы говорим о радиолокации, то там есть ошибка в измерении дальности и азимута, а в роли случайных ускорений системы выступают скорость ветра, осадки и другие погодные условия.
В нашем случае мы будем учитывать влияние шума следующим образом:

z_k=x_k+w_k, где\\z_k-измеренное\ значение\ интересуемой\ величины\ на\ k-ом\ шаге\\ x_k - истинное\ значение\ интересуемой\ величины\ на\ k-ом\ шаге\\w_k-шумовая\ добавка\ на\ k-ом\ шаге

Тогда задача фильтрации сводится к тому, чтобы максимально приблизить измеренное значение величины к истинному, а значит минимализировать шумовую добавку, на которую они отличаются.

Идея фильтра

При каждом обновлении системы мы будем получать измеренное значение, которое отлично от истинного засчёт наличия шумов. Альфа-бета фильтр позволяет частично устранить их и получить значение, близкое к истинному, используя следующий принцип: после инициализации фильтра мы делаем прогноз на следующее измерение, то есть предсказываем его значение.
Получив новое измерение мы определяем отфильтрованное значение исходя из значения, которое получили, и нашего предсказания. Чем дальше работа системы -- тем больше мы доверяем нашим предсказаниям, и тем меньше мы доверяем измерениям системы, что выражается в коэффициентах фильтра α и β, которые мы рассмотрим далее. Это происходит потому что фильтр "сходится", то есть мы считаем что наши предсказания становятся куда точнее получаемых измерений.

Описание фильтра:

Фильтрация позволяет нам получить как само значение на данном шаге k, так и скорость его изменения, а помимо этого -- экстраполяцию. Экстраполяция -- это предсказание. То есть, исходя из того, что мы уже имеем, мы можем предполагать что будет дальше. Полученные из фильтра прогноз на следующий шаг, отфильтрованное значение измеряемой величины и отфильтрованную скорость изменения измеряемой величины можно использовать по Вашему усмотрению.

Итак, для работы фильтра нам потребуется определить следующие коэффициенты:

α = \frac{2(2 k − 1)}{k(k + 1)},\ β = \frac{6}{k(k + 1)}

Они понадобятся нам для фильтрации значения и скорости его изменения. Важно понимать, что в роли этого значения может выступать что угодно, например: координата тела по x, по y или по z, дальность, угол, скорость, ускорение -- что угодно. Обратимся к формулам:

x_k=x_{k|k-1}+α(z_k-x_{k|k-1}),\\ \dot{x}_k=\dot{x}_{k|k-1}+\frac{β}{T_0}(z_k-x_{k|k-1})

z_k- измеренное\ значение\ на\ шаге\ k

x_k - отфильтрованное\ значение\ на\ шаге\ k

x_{k|k-1} - прогнозируемое\ значение\ на\ шаг\ k\ с\ шага\ {k-1}

\dot{x}_k - отфильтрованное \ значение \ скорости\ на\ шаге\ k

\dot{x}_{k|k-1} - прогнозируемое\ значение\ скорости\ на\ шаг\ k\ с\ шага\ k-1

T_0 -временной\ интервал\ между\ измерениями

α, β - коэффициенты\ фильтра

Экстраполяция, то есть прогноз, делается следующим образом:

x_{k|k-1}=x_{k-1}+T_0\dot{x}_k,\\ \dot{x}_{k|k-1}=\dot{x}_{k-1}

Оставить фильтр в таком виде было бы, на мой взгляд, ошибкой, по-скольку чем дольше мы фильтруем, тем больше kи тем меньше коэффициенты, а значит мы всё меньше доверяем измерениям и всё больше своим прогнозам, что не всегда корректно. Решением этой проблемы является определение величины k_{max}, при достижении которой мы перестаём пересчитывать коэффициенты α, β. Можно взять значение, например, равное 25 или 50.

Почему важно задавать предельное k:

Представим, что система обновляется каждую минуту. Таким образом, через 2 часа работы системы мы получим значения коэффициентов фильтра:


α = \frac{2(2 k − 1)}{k(k + 1)} = \frac{2(240− 1)}{120(120 + 1)}=0,0329...

β = \frac{6}{k(k + 1)}=\frac{6}{120(120 + 1)}=0,000413...

Тогда измеренные значения будут учитываться в достаточно малой степени. Для интереса можно измерить значения коэффициентов через 4 или 8 часов работы -- там коэффициенты будут ещё меньше.

Работа алгоритма фильтрации по шагам:

По-скольку на первых порах у нас недостаточно информации для работы фильтра, то на первых двух шагах происходит инициализация:

1) k=0: x_0 = z_0

2)k=1:x_1=z_1;\ \dot{x}_1=\frac{z_2-z_1}{T_0};\

x_{2|1}=x_1+T_0\dot{x}_1;\ \dot{x}_{2|1}=\dot{x}_1

Далее всё происходит как должно:

  1. Спустя T_0единиц времени получаем новые измерения z_k;

  2. Вычисляем коэффициенты α, β по соответствующим формулам;

  3. Фильтруем измерения и получаем значения x_kи \dot{x}_k;

  4. Делаем прогноз на следующий шаг, то есть вычисляем x_{k|k-1} и \dot{x}_{k|k-1};

Заметим, что как только величина k достигает значения k_{max} мы пропускаем второй шаг и пользуемся уже вычисленными значениями α, β коэффициентов.

Например, при k=2:

  1. Получаем z_2;

  2. α=\frac{2(4 − 1)}{2(2 + 1)}=1,\ β= \frac{6}{2(2 + 1)}=1;

  3. x_2=x_{2|1}+α(z_2-x_{2|1}),\ \dot{x}_2=\dot{x}_{2|1}+\frac{β}{T_0}(z_2-x_{2|1});

  4. x_{3|2}=x_2+T_0\dot{x}_2,\ \dot{x}_{3|2}=\dot{x}_3;

Реализация

В данной статье достаточно подробно разобраны все шаги алгоритма, приведены все формулы, поэтому реализовать код должно не составить труда, но я всё же приведу фрагмент кода на C++.

Итак, код должен иметь примерно следующий вид:

k=0;
T_0 = 5.0;

// Получаем z_k
void makeStep(double measuredValue) {
  k++;
  // Первые два шага фильтра нужны для его инициализации
  if(k == 1) {
    filteredValue = measuredValue;
    return;
  } else if(k == 2) {
    filteredVelocity = (measuredValue - filteredValue) / T_0;
    filteredValue = measuredValue;
    
    extrapolatedValue = filteredValue + (filteredVelocity * T_0);
    extrapolatedVelocity = filteredVelocity;
    return;
  }
  
  // Вычисляем коэффициенты фильтра
  alpha = (2.0 * (2.0 * k - 1.0)) / (k * (k + 1.0));
  beta = 6.0 / (k * (k + 1));
  
  // Фильтруем пришедшее значение
  filteredValue = extrapolatedValue + (alpha * (measuredValue - extrapolatedValue));
  filteredVelocity = extrapolatedVelocity + (beta / T_0 * (measuredValue - extrapolatedValue));

  // Делаем экстраполяцию, то есть прогнозируем значение на следующий шаг
  extrapolatedValue = filteredValue + (filteredVelocity * T_0);
  extrapolatedVelocity = filteredVelocity;
}

// P.S.: Как вы получите доступ к filteredValue,
// filteredVelocity, extrapolatedValue, extrapolatedVelocity -- дело Ваше.

Комментарии (21)


  1. adeshere
    00.00.0000 00:00
    #0
    +3

    чаще всего при моделировании за шум принимают АБГШ (аддитивный белый гауссовский шум),

    Спасибо, что Вы сделали это очень важное замечание! Часто этот момент упускают из вида. Но в данном случае не стоит останавливаться, сказав "А" ;-)

    Понятно, что вопрос о характеристиках шума можно разворачивать бесконечно. Но все-таки наверно тут стоило бы добавить, что есть некоторые предметные области, где предположение АБГШ абсолютно неприемлемо. Например, шумы в электронных приборах, практически все геофизические временные ряды, а также многие другие процессы - это фликкер-шум. Для геофизических временных рядов это становится особенно очевидно, если нарисовать график логарифма спектральной мощности в зависимости от логарифма частоты или периода - там будет прямая линия (см. два нижних спектра - это модельные ФШ-ряды). Изрядное число примеров для реальных рядов, и еще больше ссылок можно найти вот тут.

    Но если вы действительно столкнулись с фликкер-шумом (вместо АБГШ), то все привычные закономерности и правила применения статистических методов внезапно оказываются под огромным вопросом. Я сам не использую фильтр Калмана, так как у нас во всех временных рядах есть множество пропущенных наблюдений, а он этого очень не любит. Но несмотря на отсутствие практического опыта именно с этим фильтром, у меня есть сильные подозрения, что в случае ФШ-сигналов описанные в статье алгоритмы могут работать очень криво, особенно при больших значениях k.

    В качестве критического параметра, показывающего степень отличия реального шума от белого, можно использовать так называемый степенной параметр фликкер-шума, который обычно обозначается буквой <бета> (извините, не знаю, как тут написать что-то по-гречески). Фактически <бета> - это коэффициент линейной регрессии логарифма спектральной мощности на логарифм частоты (периода). Для белого шума он равен нулю (см. первый график), а для множества реальных процессов варьирует в диапазоне от 0.5 до 2.0 (примеры см. там же).

    Понятно, что <бета>=2.0 - это процесс с независимыми случайными приращениями. (Прямой поиск термина приводит на вот эту страницу, но, на мой вкус, она менее удачно написана, и лучше лазить по первой ссылке). Для таких временных рядов обычные статистические методы заведомо не работают. Но даже при значениях <бета> порядка 1 все тоже может быть очень плохо.

    В общем, практический совет такой: обязательно проверяйте спектр шума, прежде чем выбирать метод фильтрации. И если вдруг степенной параметр <бета> окажется порядка единицы или больше, то семь раз протестируйте алгоритм на моделях, прежде чем один раз его применить ;-)

    Кстати, если кому-то для тестов понадобятся фрактальные временные ряды, то вот тут выложен пакет из 200 модельных рядов, сгенерированных по алгоритму Фосса. Мне самому было бы очень интересно взглянуть на результаты фильтрации разных модельных сигналов, на которые вместо белого шума наложен "фрактальный", или фликкерный шум. Если вдруг у Вас будет желание и возможность провести такое тестирование - пишите в личку, постараюсь помочь, чем смогу.


  1. Zara6502
    00.00.0000 00:00
    #25226638
    +8

    прежде всего для новичков, которые ничего не понимают в фильтрации

    в фильтрации чего?

    Прочитал Введение, но пока не понял о чем статья.

    Прочитал раздел "Фильтр Калмана" и пока всё равно не понял о чем статья. (могу конечно лезть в википедию, но вы же в самом начале написали что статья для новичков)

    Фильтрация позволяет нам получить как само значение на данном шаге

    Значение чего?

    Всё это можно использовать по Вашему усмотрению

    Что "это"?

    Ну а теперь в википедию:

    Фильтр Калмана широко используется в инженерных и эконометрических приложениях: от радаров и систем технического зрения до оценок параметров макроэкономических моделей[1][2]. Калмановская фильтрация является важной частью теории управления, играет большую роль в создании систем управления. Совместно с линейно-квадратичным регулятором фильтр Калмана позволяет решить задачу линейно-квадратичного гауссовского управления. Фильтр Калмана и линейно-квадратичный регулятор — возможное решение большинства фундаментальных задач в теории управления.

    Где используется[править | править код]


    1. SpiderEkb
      00.00.0000 00:00
      #25226918
      +2

      в фильтрации чего?

      Некоторой измеряемой величины, содержащей погрешности измерения. Задача фильтрации - свести шумы к минимуму.

      Что это может быть - да что угодно. Например, координаты с GPS приемника...


    1. BadHandycap
      00.00.0000 00:00
      #25227378
      +2

      в фильтрации чего?

      Сигнала. Чего же еще. Не воды же.


      1. ayv2004
        00.00.0000 00:00
        #25236842
        -1

        Читайте статистическую радиотехнику, радиолокацию, навигацию и другую литеру где изуяатся вопросы оценок случайных процессов..


        1. BadHandycap
          00.00.0000 00:00
          #25238670
          +1

          К чему вы мне это написали?


    1. Omazz Автор
      00.00.0000 00:00
      #25227864
      +1

      Здравствуйте! Согласен с Вами, моя вина -- не указал область применения и обстоятельства, которые обеспечивают необходимость фильтра. Поправил Disclaimer.


      1. Zara6502
        00.00.0000 00:00
        #25230892

        Здравствуйте, но что такое "шум" в контексте обозначенной темы и причем тут экономика? (открою секрет, особенно двум товарищам выше - я в теме и всё понимаю, просто я до занудства не люблю материалы, которые не выдерживают академические стандарты. Но раз вы в самом начале написали слово "новичок", то материал должен быть другим. Ну или уберите "новичка", но тогда не ясно для кого материал)


        1. Omazz Автор
          00.00.0000 00:00
          #25231120

          Про шум в контексте обозначенной темы:
          Да, Вы правы, нужно было добавить как минимум следующее:
          z = x + w, где
          z -- измеренная величина
          x -- величина истинная
          w -- шумовая добавка
          Шум, как минимум, обусловлен погрешностью измерительных приборов, случайными ускорениями модели. (например, если мы фильтруем координаты какого-нибудь летательного аппарата, то это может быть поправка на скорость ветра, погодные условия)
          Про экономику:
          В экономику также есть случайные ускорения. Я работаю в сфере радиолокации, но очень часто когда мне приходилось искать алгоритмы экстраполяции и фильтрации я натыкался на вполне понятные объяснения, представленные в виде лекций ВШЭ(высшей школы экономики). Эти лекции, соответственно, предназначались для экономики. На всякий случай, приведу СУБЪЕКТИВНЫЙ пример в достаточно свободной форме:
          Мы мониторим цену на пиццу в ближайшем кафе по типу месяц--средняя цена за кусок. В мае очень много праздников, пиццу заказывают часто, в связи с этим хитрый хозяин кафе решил уменьшить цену в 2 раза по определённым датам, чтобы пицца была ещё привлекательной. Именно это и является шумом, случайным ускорением. Да, цена действительно уменьшилась в 2 раза, что не соответствовало экстраполяции, но цена уменьшается только в определённые дни.
          То есть, для получения адекватной оценки средней цены за кусок, нужно как-то сгладить этот майский скачок вниз, а фильтр как раз таки поможет нам это сделать.
          В роли "ошибки измерительного прибора" может выступать то, что человеку, который замерял цену на кусок, в какой-то из дней стало лень идти её смотреть и он просто написал в своей выборке данных цену, которая была в прошлый раз.

          Степень фильтрации зависит от параметров фильтра и от его "вида", я ни в коем случае не агитирую пихать везде альфа-бета фильтр, но почему бы не попробовать хотя бы промоделировать такую систему и посмотреть на результат.
          P.S.: Вечером постараюсь отредактировать статью в соответствии с Вашим замечанием, чтобы внести ясность для читателей. Спасибо за дельный совет. Прошу отнестись с пониманием и снисхождением к примеру выше -- он придумывался прямо во время написания комментария, очень хочется быть хорошим специалистом и свободно общаться на эту тему, а для этого нужно прежде всего пробовать, на мой взгляд.


          1. Zara6502
            00.00.0000 00:00
            #25235424
            +1

            я же без наезда, я лишь отметил что материал для "новичка" подразумевает несколько более широкий охват как используемых терминов и разъяснений, так и глубины освещения вопроса - не каждый новичок смирится с необходимостью читать параллельно со статьёй гугл/яндекс.

            касательно шума - слово у обывателя ассоциируется в 99% случаев со звуком, но имеет несколько более широкое применение в математических методах и алгоритмах. Дополнительное объяснение поможет в этом сориентироваться например тем, кто читает материал на уровне научпопа.

            Я бы рекомендовал для терминов или писать короткие сноски или делать ссылкой на вики. Тема-то очень интересная и самое главное для многих кажущаяся ненужной или какой-то узкоспециальной. Я с "шумом" столкнулся при обработке изображений и их фильтрации, думал нахвататься верхушек да забыть, но вот 25 лет прошло, а я даже не слишком-то и погрузился в тему.

            На вас подписан, буду ждать еще статьи, буду рад если напишете что-то про фильтры для изображений, если это входит в вашу область применения.


            1. Omazz Автор
              00.00.0000 00:00
              #25235566

              Фильтрация изображений была у меня в ВУЗе, на практике не использовал.
              Разбирали достаточно много алгоритмов, всё с примерами, отчёты по лабораторным были 50+ (иногда 100+) страниц, был очень сильный преподаватель, который работает в этой сфере и это основной его вид деятельности. Сейчас пишу диплом, при первой возможности -- продолжу развивать данную тематику, спасибо Вам за обратную связь!


  1. ksbes
    00.00.0000 00:00
    #25226922

    Слишком кратко. Нет ответа внятного на вопрос «почему так?» Т.е. нужно было либо самому почти ничего не писать, оставив ссылки на википедию. И сосредточится на описании процесса программирования. И смысла кода.
    Либо как-то популярно объяснить общий принцип до формул. Раз уж код не объясняете.

    А так — и не то и не сё.


    1. Omazz Автор
      00.00.0000 00:00
      #25227862

      Здравствуйте!
      Писал код с комментариями, всё делал по вышеописанным мной шагам -- надеялся, что поможет. Согласен, что по-хорошему здесь нужна моделирующая программа, выложенная на гитхаб для демонстрации работы фильтра.
      "Либо как-то популярно объяснить общий принцип до формул. Раз уж код не объясняете." -- попробовал это сделать во фрагменте "Идея фильтра".


  1. homesoft
    00.00.0000 00:00
    #25227350

    А что, alpha и beta должны со временем быстро стремиться к 0 ?


    1. Omazz Автор
      00.00.0000 00:00
      #25227848

      Достаточно быстро
      Добавил маленький фрагмент в статье, где разобрал на примере.


  1. adeshere
    00.00.0000 00:00
    #25229562
    +3

    чаще всего при моделировании за шум принимают АБГШ (аддитивный белый гауссовский шум),

    Спасибо, что Вы сделали это очень важное замечание! Часто этот момент упускают из вида. Но в данном случае не стоит останавливаться, сказав "А" ;-)

    Понятно, что вопрос о характеристиках шума можно разворачивать бесконечно. Но все-таки наверно тут стоило бы добавить, что есть некоторые предметные области, где предположение АБГШ абсолютно неприемлемо. Например, шумы в электронных приборах, практически все геофизические временные ряды, а также многие другие процессы - это фликкер-шум. Для геофизических временных рядов это становится особенно очевидно, если нарисовать график логарифма спектральной мощности в зависимости от логарифма частоты или периода - там будет прямая линия (см. два нижних спектра - это модельные ФШ-ряды). Изрядное число примеров для реальных рядов, и еще больше ссылок можно найти вот тут.

    Но если вы действительно столкнулись с фликкер-шумом (вместо АБГШ), то все привычные закономерности и правила применения статистических методов внезапно оказываются под огромным вопросом. Я сам не использую фильтр Калмана, так как у нас во всех временных рядах есть множество пропущенных наблюдений, а он этого очень не любит. Но несмотря на отсутствие практического опыта именно с этим фильтром, у меня есть сильные подозрения, что в случае ФШ-сигналов описанные в статье алгоритмы могут работать очень криво, особенно при больших значениях k.

    В качестве критического параметра, показывающего степень отличия реального шума от белого, можно использовать так называемый степенной параметр фликкер-шума, который обычно обозначается буквой <бета> (извините, не знаю, как тут написать что-то по-гречески). Фактически <бета> - это коэффициент линейной регрессии логарифма спектральной мощности на логарифм частоты (периода). Для белого шума он равен нулю (см. первый график), а для множества реальных процессов варьирует в диапазоне от 0.5 до 2.0 (примеры см. там же).

    Понятно, что <бета>=2.0 - это процесс с независимыми случайными приращениями. (Прямой поиск термина приводит на вот эту страницу, но, на мой вкус, она менее удачно написана, и лучше лазить по первой ссылке). Для таких временных рядов обычные статистические методы заведомо не работают. Но даже при значениях <бета> порядка 1 все тоже может быть очень плохо.

    В общем, практический совет такой: обязательно проверяйте спектр шума, прежде чем выбирать метод фильтрации. И если вдруг степенной параметр <бета> окажется порядка единицы или больше, то семь раз протестируйте алгоритм на моделях, прежде чем один раз его применить ;-)

    Кстати, если кому-то для тестов понадобятся фрактальные временные ряды, то вот тут выложен пакет из 200 модельных рядов, сгенерированных по алгоритму Фосса. Мне самому было бы очень интересно взглянуть на результаты фильтрации разных модельных сигналов, на которые вместо белого шума наложен "фрактальный", или фликкерный шум. Если вдруг у Вас будет желание и возможность провести такое тестирование - пишите в личку, постараюсь помочь, чем смогу.


    1. Omazz Автор
      00.00.0000 00:00
      #25229642

      Спасибо Вам большое за такой развёрнутый комментарий!

      По поводу пропущенных наблюдений: они есть во многих системах, но ведь экстраполяция может спасти? Не претендую на правду, но могу предложить Вам попробовать МНК, а позже и взвешенный МНК(например последнему наблюдения давать больше веса, чем тем что были раннее). На самом деле, экстраполяция, которая представлена в статье, является очень слабой, но она содержится в оригинальном описании фильтра, поэтому я решил ничего не менять.

      По поводу шумов: слышал про такое, но что-то серьёзное увидел впервые только сейчас от Вас. Буду разбираться, изучу этот момент. Спасибо Вам.


  1. Truenya
    00.00.0000 00:00
    #25229574
    -1

    Да ладно бы альфа и бета стремились к нулю.
    У вас фильтрованное и экстраполированное значение и скорость также к нулю стремятся.

    Попробовал вместо одной из своих самописок на тему одномерной фильтрации в рабочий проект подставить, поотлаживаться, сравнить точность.

    Результат удручил, ну автор, ну зачем ты так?


    1. Omazz Автор
      00.00.0000 00:00
      #25229584

      Доброго времени суток! Приведённый мной алгоритм используется во вполне рабочих проектах ровно в том виде, в котором я его здесь описал. Вы точно перестаёте пересчитывать коэффициенты альфа и бета? На каком шаге Вы это делаете? Как часто обновляются данные? Давайте вместе искать решение. Попробуйте фиксировать значения альфа и бета при k=10, а позже при k=15 и так по-тихоньку увеличивайте значение, если результат будет улучшаться.

      P.S.: Посмотрите внимательно на формулы, экстраполированные значения сами по себе ну никак не могут стремиться к нулю, в общем случае дак точно. Можете прислать мне строчки кода, попробую помочь.


      1. Truenya
        00.00.0000 00:00
        #25300792

        Вообще да, фиксация коэффицентов вполне может помочь.

        Там ситуация такая, что:

        1. разброс измеряемой величины примерно равен её значению.

        2. Величина изменяется линейно на отрезках, а не на всём протяжении измерений

        3. Слишком большое влияние изменений величины на первых шагах исказило результат.


        1. Omazz Автор
          00.00.0000 00:00
          #25304898

          Вообще да, фиксация коэффицентов вполне может помочь.

          Не думаю, что правильно использовать фильтр без фиксации коэффициентов. Я в статье прям пример привёл, почему так делать не стоит. (Возможно, он был дописан уже после Вашего комментария)

          Давайте попробуем пройтись по пунктам.

          1. разброс измеряемой величины примерно равен её значению.

          Получается, что у нас очень большие значения шума.

          2. Величина изменяется линейно на отрезках, а не на всём протяжении измерений

          Получается, что мы знаем, когда эти отрезки начинаются? А Вы гоните фильтр всё время, или только на этих отрезках начинаете инициализацию? Тут нужно смотреть на то, что вы измеряете и как оно себя ведёт.

          3. Слишком большое влияние изменений величины на первых шагах исказило результат.

          Понятно -- инициализация фильтра по сильно зашумлённым данным задало нам неправильное значение скорости изменения величины, а далее фильтр пытается его выровнять всё время. Тогда может стоит попробовать инициализировать фильтр на тех участках где шумы минимальны?

          P.S.: Вообще это может быть из-за откровенно слабой экстраполяции в этом фильтре. Если Вы умеете использовать МНК, я бы предложил Вам попробовать его. Всё хочу написать статью по этому поводу, где разобрал бы метод наименьших квадратов на конкретных примерах. Хочу показать эффективность альфа-бета фильтра с ним и без него, но пока что руки не доходят, хотя различия там колоссальные -- я такое уже и моделировал, и не только.


  1. SpiderEkb
    00.00.0000 00:00
    #25235250
    +1

    Вообще говоря, не Калманом единым. Многие рекурсивные фильтры (и Калман в том числе) уходят корнями в обычный LowPass фильтр

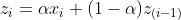
    а дальше уже вариации на тему коэффициентов.

    В качестве более простой (но во многих случаях работающее не хуже) альтернативы Калману можно рассматривать экспоненциальное сглаживание (обычное, двойное, тройное)

    Для выявления линии тренда в ряде случаев неплохо подойдет фильтр Ходрика-Прескотта (хотя он не является рекурсивным как Калман, LowPass, экспоненциальное сглаживание и более сложен вычислительно).

    Калман (в его различных модификациях) хорош в тех случаях, когда известна закономерность по которой можно предсказывать следующее значение наблюдаемых данных (модель процесса). Например, если мы знаем скорость и ускорение, то можем предсказывать следующее значение координат и затем сравнивать их с наблюдаемым. И в общем случае фильтр Калмана работает с матрицами - текущего состояния, эволюции, апостериорного состояния, наблюдений, управления.

    И в тех случаях, когда модель процесса неизвестна (нет возможности построить матрицу управления), сглаживание может работать ничуть не хуже но быть проще в реализации.