Привет, Хабр!

В этой статье представлен алгоритм быстрого поиска подграфов, изоморфных заданному, рассматриваются только направленные графы.

Сначала будет приведён алгоритм поиска паттернов рекуррентным перебором, потом его быстрая модификация с минимальным отсечением.

Примеры кода написаны на C++, исходники всей библиотеки лежат здесь. Также написана копия библиотеки на Java, исходники лежат здесь.

Изоморфизм​

Два графа являются изоморфными тогда и только тогда, когда их вершины можно пронумеровать так, чтобы по составленному соответствию между номерами вершин одного и другого графа выполнялось правило: если две вершины соединены ребром в одном графе, то вершины во втором графе с соответствующими номерами тоже должны иметь общее ребро. Это соответствие принято называть изоморфной подстановкой

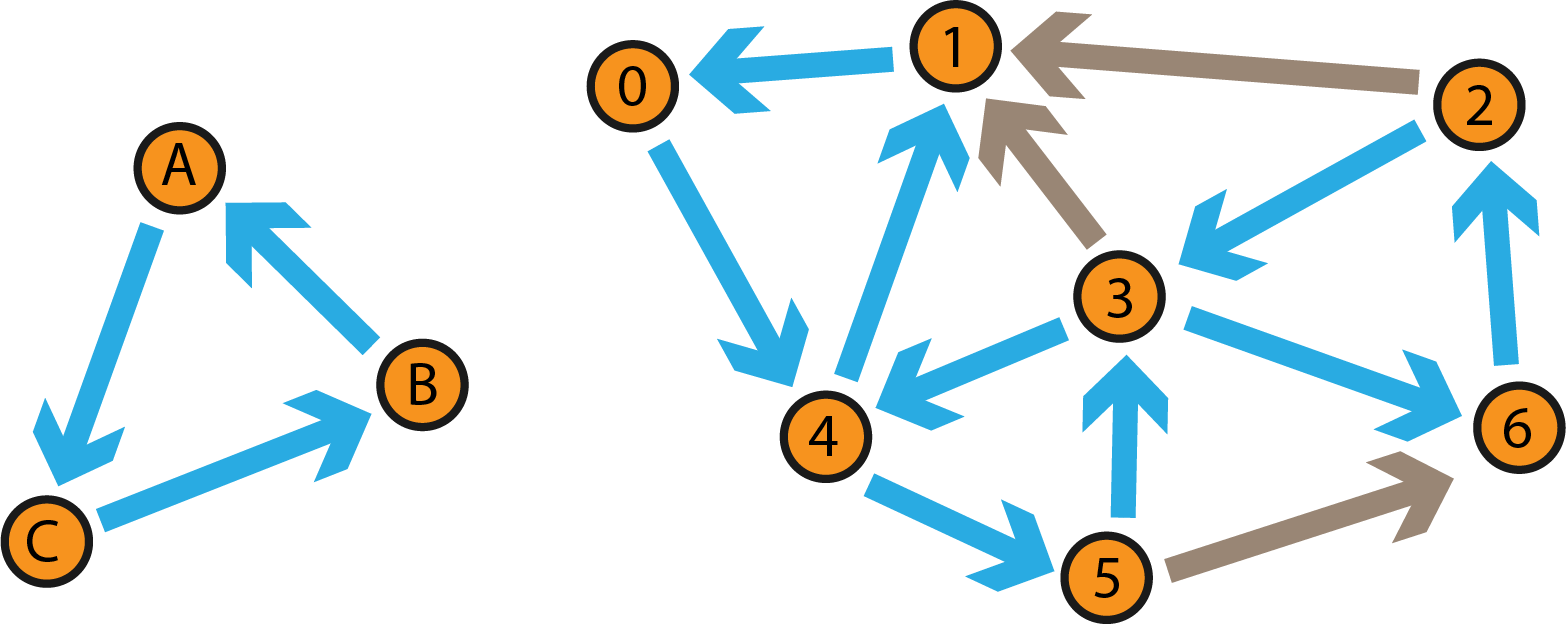
Проверим два графа на изоморфность:

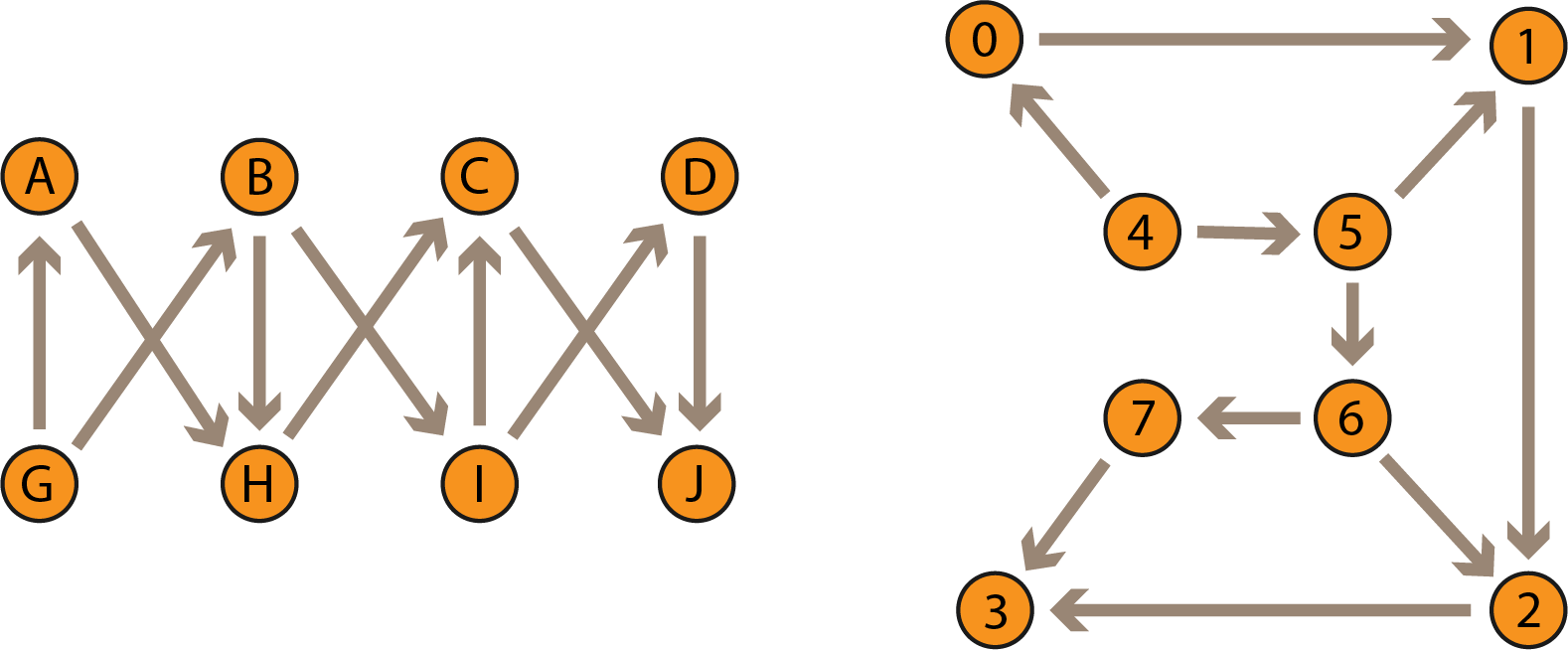
Т.к. подстановка

обеспечит попарное соответствие всех рёбер двух графов, то графы изоморфны.

Любой пронумерованный граф можно описать матрицей смежности. Причём при изменении нумерации будет меняться и матрица смежности одного и того же графа.

Номеру строки соответствует номер вершины из которой идёт ребро, а номеру столбца - номер вершины, в которую идёт ребро.

Если ребра между двумя вершинами нет, то соответствующий элемент матрицы смежности оставляется пустым, если есть, то ставится x. Если граф взвешенный, то вместо x ставится вес ребра, а при отсутствии ребра ставится 0

Например, матрица смежности левого графа (не взвешенного) будет иметь вид:

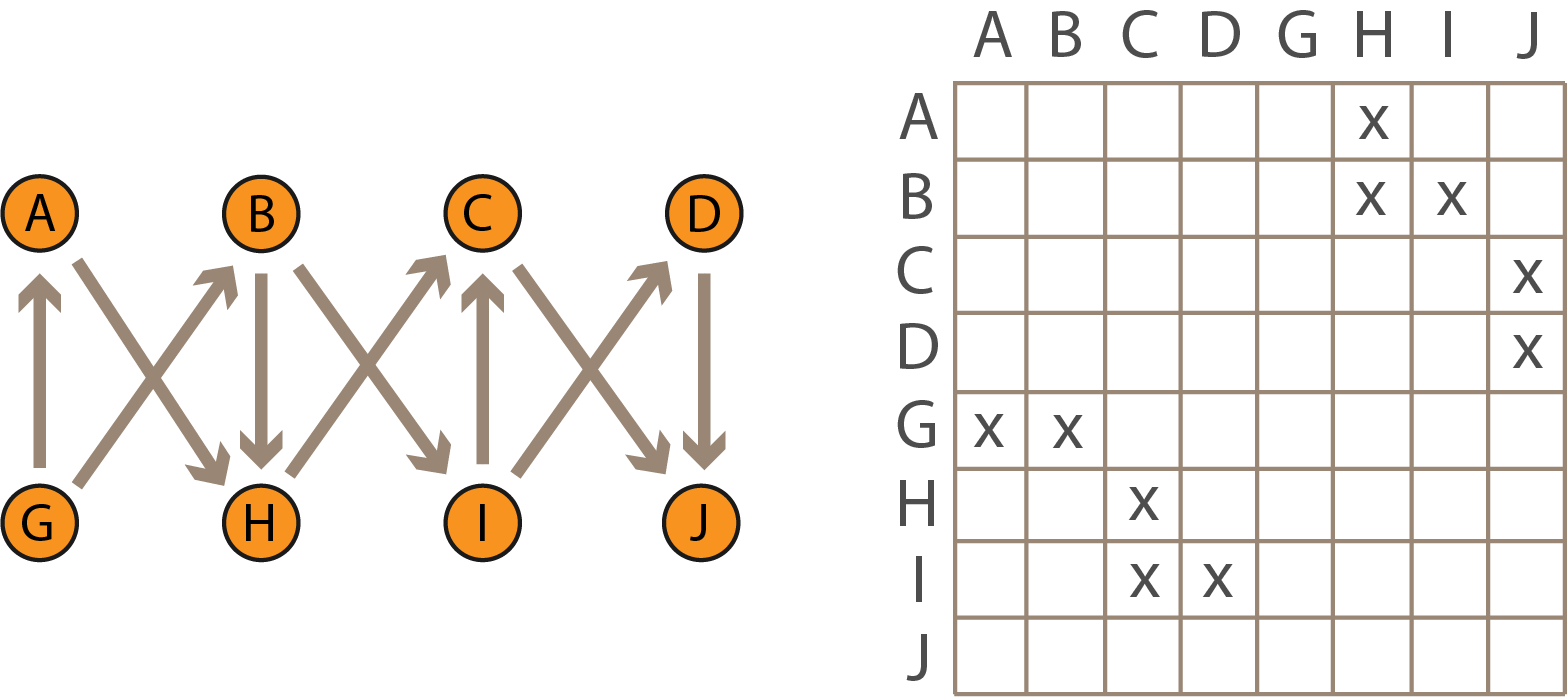
А матрица правого графа будет такой:

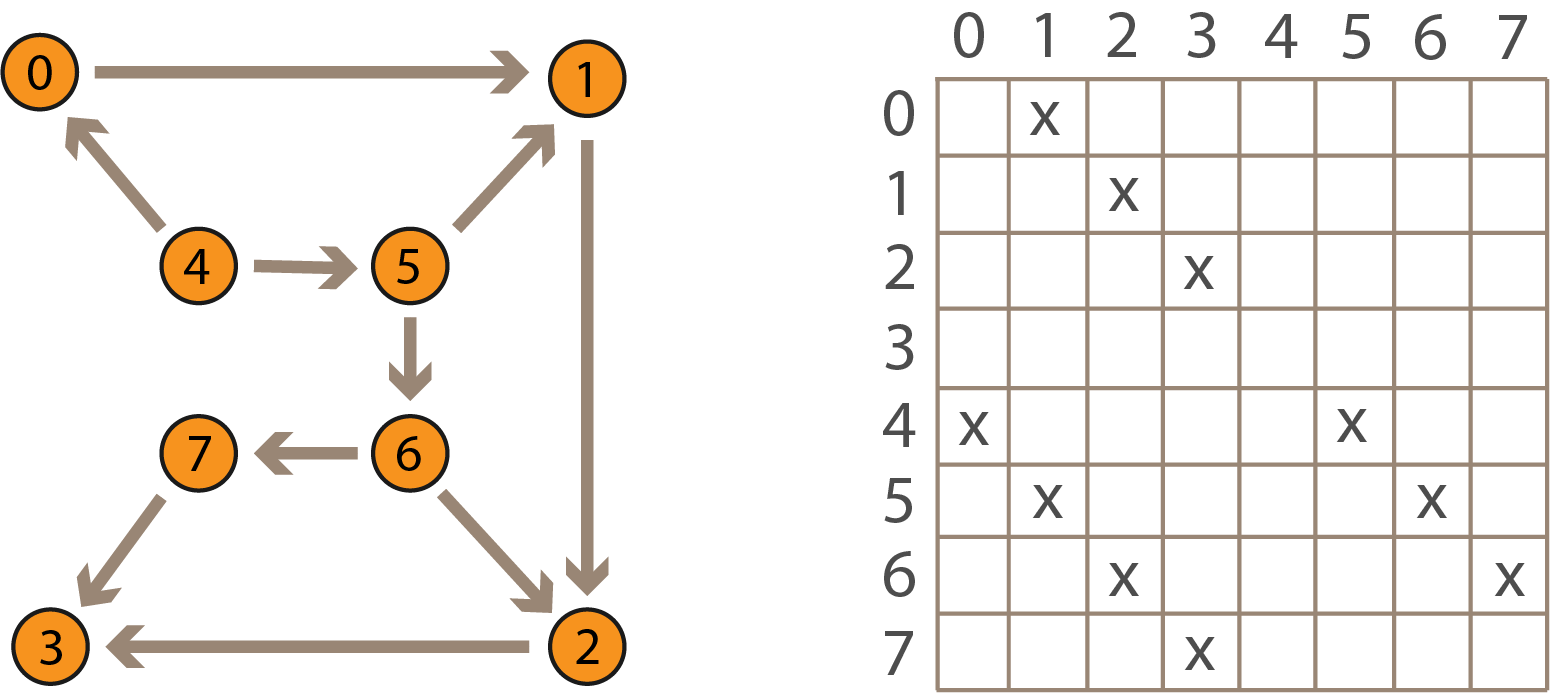
Хотя графы изоморфны, матрицы их смежности сильно отличаются. В дальнейшем будем рассматривать только взвешенные графы.

Перестановки​

Если оба графа уже записаны с помощью матриц смежности M1​ и M2​, то задача сводится к поиску такой перестановки матрицы M1​, чтобы переставленная матрица p(M1​) совпала матрицей M2​. Перестановку p(M) будем называть изоморфной.

Чтобы построить перестановку матрицы, нужно заполнить массив неповторяющимися значениями от 0 до n−1. Элемент с индексом i показывает, какой номер будут иметь строка или столбец в новой матрице, если в старой они имели индекс i.

Если вернуться к изоморфной подстановке из прошлого блока, то перестановку можно получить, взяв значения из нижней строки:

Так можно сделать, потому что верхняя строка упорядоченна.

Выполнить перестановку p матрицы source можно следующим образом:

/**
 * Применить перестановку к матрице
 *
 * @param source источник
 * @param sz     размер перестановки
 * @param p      перестановка
 * @return переставленная матрица
 */
int **makePermute(int **source, int sz, const int *p) {
    int **res = new int *[sz];
    for (int i = 0; i < sz; i++)
        res[i] = new int[sz];

    for (int i = 0; i < sz; i++)
        for (int j = 0; j < sz; j++)
            res[i][j] = source[p[i]][p[j]];

    return res;
}

Теперь составим массив перестановки

int p[8]{0, 5, 2, 7, 4, 1, 6, 3};  

и проверим, что, применив эту перестановку, мы получим из матрицы левого графа матрицу правого:

#include <vector>
#include "misc/combinatorics.h"

int main() {
    // перестановка
    int p[8]{0, 5, 2, 7, 4, 1, 6, 3};

    // матрица смежности 
    int sourceMatrix[8][8]{
            {0, 0, 0, 0, 0, 1, 0, 0},
            {0, 0, 0, 0, 0, 1, 1, 0},
            {0, 0, 0, 0, 0, 0, 0, 1},
            {0, 0, 0, 0, 0, 0, 0, 1},
            {1, 1, 0, 0, 0, 0, 0, 0},
            {0, 0, 1, 0, 0, 0, 0, 0},
            {0, 0, 1, 1, 0, 0, 0, 0},
            {0, 0, 0, 0, 0, 0, 0, 0},
    };
    // подготавливаем матрицу
    int **source = new int *[8];
    for (int i = 0; i < 8; i++) {
        source[i] = new int[8];
        for (int j = 0; j < 8; j++)
            source[i][j] = sourceMatrix[i][j];
    }

    // получаем переставленную матрицу
    int **permuted = makePermute(source, 8, p);

    // выводим её на консоль
    for (int i = 0; i < 8; i++) {
        for (int j = 0; j < 8; j++)
            std::cout << permuted[i][j] << " ";
        std::cout << std::endl;
    }

    return 0;
}

На консоль будет выведено:

Поиск изоморфных перестановок​

Чтобы проверить, является ли одна матрица заданной перестановкой другой написан метод  arePermutatedEquals():

/**
 * Проверка переставленной подматрицы на равенство целевой матрице;
 * Этот метод проверяет, что каждому ненулевому элементу образца
 * должен соответствовать ненулевой элемент в переставленной матрице.
 * В случае жёсткой проверки каждому нулевому элементу целевой матрицы должен
 * соответствовать нулевой элемент переставленной матрицы
 *
 * @param p          перестановка
 * @param source     матрица-источник
 * @param target     матрица-цель
 * @param sourceSum  степени вершин у графа-источника
 * @param targetSum  степени вершин у графа-цели
 * @param sz         размер стороны матриц
 * @param hardCheck  флаг, нужна ли жёсткая проверка
 * @return - флаг, является ли одна матрица перестановкой другой
 */
bool arePermutatedEquals(
        const int *p, int **source, int **target, const int *sourceSum, const int *targetSum,
        int sz, bool hardCheck
) {
    // проверяем, что у графов совпадают степени вершин
    for (int i = 0; i < sz; i++)
        // или их степень меньше степени в паттерне
        if (hardCheck && sourceSum[p[i]] < targetSum[i])
            return false;

    // перебираем все вершины
    for (int i = 0; i < sz; i++)
        // снова перебираем все вершины
        for (int j = 0; j < sz; j++) {
            // если проверка жёсткая, и элемент из переставленной не совпадает с соответствующим
            // элементом из целевой матрицы
            if (hardCheck && target[i][j] != source[p[i]][p[j]])
                // возвращаем флаг, что матрицы не равны
                return false;
            // если проверка нежёсткая, элемент целевой матрицы не равен 0
            // и при этом элемент из переставленной не совпадает с соответствующим
            // элементом из целевой матрицы
            if (!hardCheck && target[i][j] != 0 && target[i][j] != source[p[i]][p[j]])
                // возвращаем флаг, что матрицы не равны
                return false;
        }
    // если не встречено неравных элементов, то возвращаем флаг, что матрицы равны
    return true;
}

Чтобы найти все изоморфные перестановки двух матриц перебором, необходимо построить все перестановки заданной длины, после чего для каждой проверить, связаны ли рассматриваемые матрицы этой перестановкой или нет.

Чтобы перебрать все перестановки, используется рекуррентный метод перебора. Для каждой найденной перестановки выполняется lambda-выражение, переданное в параметрах.

/**
 * функция-генератор перестановок
 *
 * @param p         текущая перестановка
 * @param pos       положение
 * @param source    матрица-источник
 * @param target    матрица-цель
 * @param sourceSum суммы у источника
 * @param targetSum суммы цели
 * @param hardCheck флаг, нужна ли жёсткая проверка
 * @param consumer  обработчик найденной перестановки лямбда выражение (int *c)->{}
 */

template<typename F>
void generatePermutationsStep(int sz, int *p, int pos, const F &consumer) {
    // Если мы дошли до последнего элемента
    if (pos == sz - 1) {
        consumer(p);
    } else  // иначе
        // Перебираем все оставшиеся элементы
        for (int i = pos; i < sz; i++) {
            // Меняем местами текущий элемент и перебираемый
            std::swap(p[i], p[pos]);
            // Вызываем рекурсию для следующего элемента
            generatePermutationsStep(sz, p, pos + 1, consumer);
            // Меняем местами обратно
            std::swap(p[i], p[pos]);
        }
}

/**
 * функция-генератор перестановок
 *
 * @param size     количество элементов перестановка
 * @param consumer обработчик найденной перестановки лямбда выражение (int *c)->{}
 */
template<typename F>
void generatePermutations(int size, const F &consumer) {
    // стартовая перестановка - последовательность индексов от 0 до target.length-1
    int startP[size];
    for (int i = 0; i < size; i++)
        startP[i] = i;

    // запускаем генерацию перестановок
    generatePermutationsStep(size, startP, 0, consumer);
}

С помощью generatePermutations() написан метод getAllIsomorphicPermutations(). Он возвращает множество изоморфных перестановок, которые связывают две матрицы, полученные в аргументах.

/**
 * Поиск всех перестановок исходной матрицы таких, что переставленная матрица совпадает
 * с целевой. Перестановка - это просто последовательность индексов всех вершин,
 * составляя по которым новую матрицу, мы получим целевую
 *
 * @param source    матрица-источник
 * @param target    целевая матрица
 * @param sz        размер стороны матриц
 * @param hardCheck флаг, нужна ли жёсткая проверка; если `hardCheck` равен `false`, то нулевому элементу целевой
 *                  матрицы может соответствовать произвольное значение в переставленной матрице, а если
 *                  `true`, то все элементы целевой и переставленной матриц должны полностью
 *                  совпадать
 * @return список всех перестановок исходной матрицы таких, что переставленная матрица совпадает
 * с целевой
 */
std::unordered_set<CombinatoricsData, CombinatoricsData::HashFunction>
getAllIsomorphicPermutations(int **source, int **target, int sz, bool hardCheck) {
    // степени вершин
    int *sourceSum = getPowers(source, sz);
    int *targetSum = getPowers(target, sz);

    // множество перестановок
    std::unordered_set<CombinatoricsData, CombinatoricsData::HashFunction> ps;
    // запускаем генерацию перестановок
    generatePermutations(
            sz,
            [&ps, &sz, &source, &target, &hardCheck, &targetSum, &sourceSum](int *p) {
                // если подграф изоморфен паттерну по рассматриваемой перестановке
                if (arePermutatedEquals(p, source, target, sourceSum, targetSum, sz, hardCheck))
                    // добавляем эту перестановку в множество изоморфных перестановок
                    ps.insert(CombinatoricsData(p, sz));
            });
    return ps;
}

CombinatoricsData - специальный класс-обёртка над целочисленным массивом для работы с коллекциями, метод int * getData() возвращает указатель на хранящиеся в массиве данные.

Проверим, что алгоритм найдёт правильную перестановку от левого графа к правому:

#include <vector>
#include "misc/combinatorics.h"
#include "patternResolver.h"

int main() {
    // матрица смежности 
    int sourceMatrix[8][8]{
            {0, 0, 0, 0, 0, 1, 0, 0},
            {0, 0, 0, 0, 0, 1, 1, 0},
            {0, 0, 0, 0, 0, 0, 0, 1},
            {0, 0, 0, 0, 0, 0, 0, 1},
            {1, 1, 0, 0, 0, 0, 0, 0},
            {0, 0, 1, 0, 0, 0, 0, 0},
            {0, 0, 1, 1, 0, 0, 0, 0},
            {0, 0, 0, 0, 0, 0, 0, 0},
    };
    // матрица смежности 
    int targetMatrix[8][8]{
            {0, 1, 0, 0, 0, 0, 0, 0},
            {0, 0, 1, 0, 0, 0, 0, 0},
            {0, 0, 0, 1, 0, 0, 0, 0},
            {0, 0, 0, 0, 0, 0, 0, 0},
            {1, 0, 0, 0, 0, 1, 0, 0},
            {0, 1, 0, 0, 0, 0, 1, 0},
            {0, 0, 1, 0, 0, 0, 0, 1},
            {0, 0, 0, 1, 0, 0, 0, 0},
    };
    // подготавливаем матрицу
    int **source = new int *[8];
    for (int i = 0; i < 8; i++) {
        source[i] = new int[8];
        for (int j = 0; j < 8; j++)
            source[i][j] = sourceMatrix[i][j];
    }
    // подготавливаем матрицу
    int **target = new int *[8];
    for (int i = 0; i < 8; i++) {
        target[i] = new int[8];
        for (int j = 0; j < 8; j++)
            target[i][j] = targetMatrix[i][j];
    }

    std::unordered_set<CombinatoricsData, CombinatoricsData::HashFunction>
            cds = getAllIsomorphicPermutations(source, target, 8, true);

    for (CombinatoricsData cd: cds) {
        for (int k = 0; k < cd.getSize(); k++)
            std::cout << cd.getData()[k] << " ";
        std::cout << std::endl;
    }

    return 0;
}

На консоль будет выведено:

Полученная перестановка совпадает с определённой ранее:

Поиск паттернов​

Пусть у нас определено два графа: большой и малый. Нам требуется найти все такие подграфы большого графа, что они будут изоморфны малому. Большой граф будем называть дата-графом, малый - паттерном.

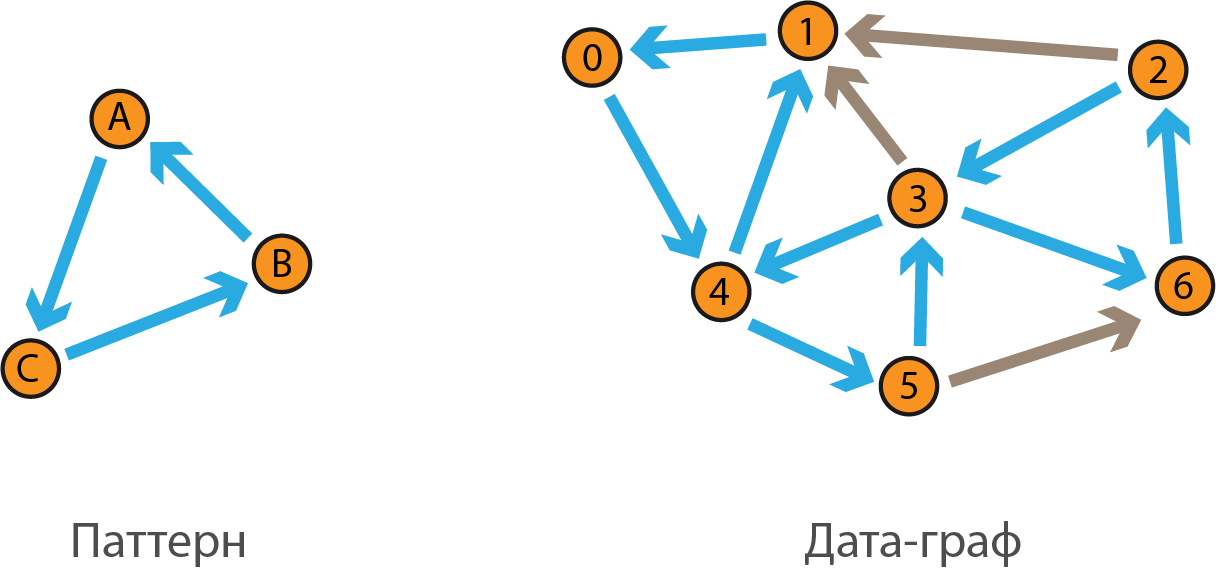
На рисунке слева изображён паттерн ABC, справа - дата-граф 0123456.

В дата-графе паттерну изоморфны три подграфа:

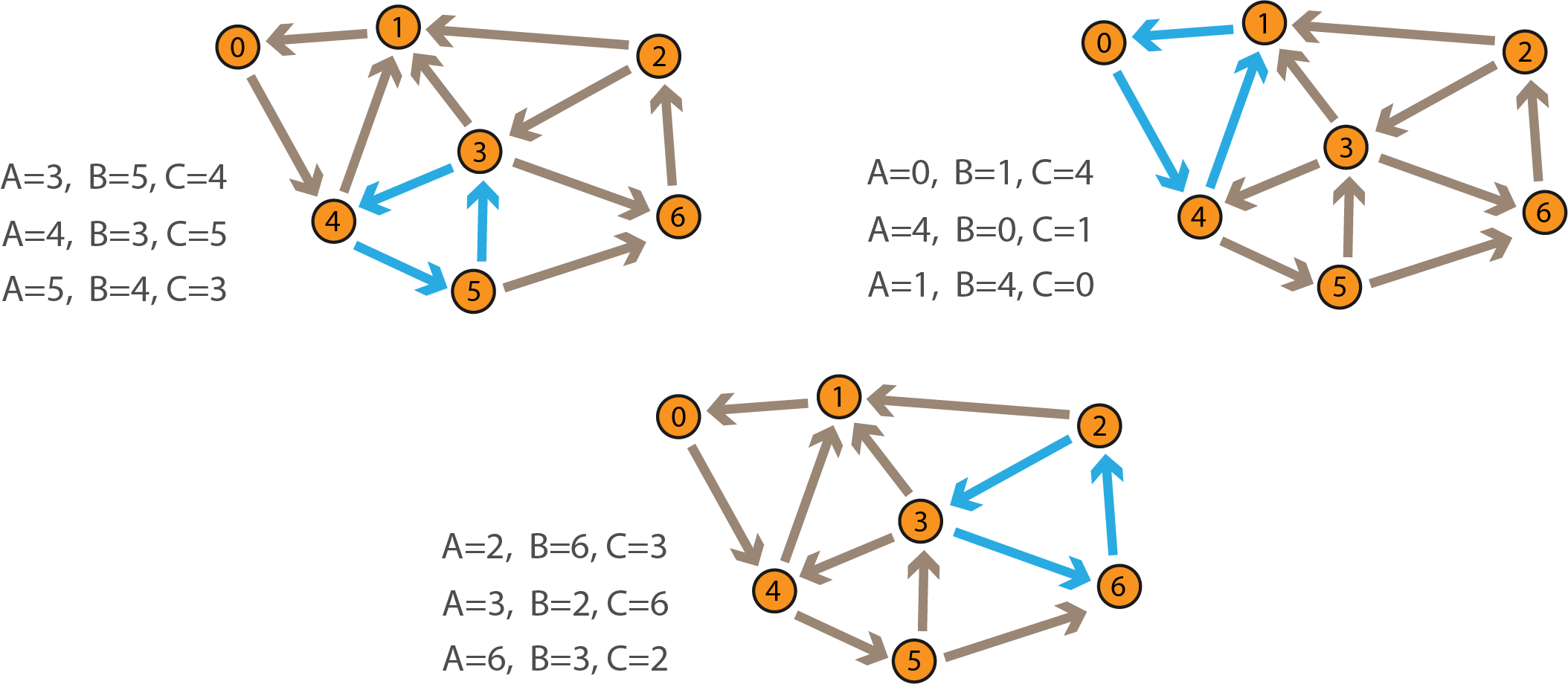
При этом каждый подграф связан тремя разными комбинациями точек. Такое число комбинаций обусловлено тем, что паттерн симметричен. Если бы в нём совсем не было симметрии, то на каждый подграф приходилась бы ровно одна комбинация. Будем называть такие комбинации изоморфными.

Чтобы найти все изоморфные подграфы перебором, нужно перебрать все возрастающие комбинации вершин дата-графа длины, равной количеству вершин паттерна. Затем нужно построить по ним матрицы смежности и проверить их на изоморфность матрице смежности паттерна.

Функция перебора упорядоченных комбинаций устроена аналогично функции перебора перестановок:

/**
 * Запустить перебор комбинаций
 *
 * @param n        общее число элементов
 * @param k        размер комбинации
 * @param consumer обработчик для каждой найденной комбинации (const int *c)->{}
 */
template<typename F>
void combine(int n, int k, const F &consumer) {
    if (k > n)
        throw std::invalid_argument(
                "combine() arr size: " + std::to_string(n) + " elements count " + std::to_string(k)
        );
    // запускаем первый шаг перебора комбинаций
    combineStep(new int[k], k, 0, n - 1, 0, consumer);
}

/**
 * Шаг перебора комбинаций
 *
 * @param consumer    обработчик для каждой найденной комбинации
 * @param combination текущая комбинация
 * @param min         минимальное значение для перебора
 * @param max         максимальное значение для перебора
 * @param pos         индекс текущего элемента
 */
template<typename F>
void combineStep(int *combination, int sz, int min, int max, int pos, const F &consumer) {
    // если индекс текущего элемента равен длине комбинации,
    if (pos == sz)
        // значит, она составлена, передаём её обработчику
        consumer(combination);
        // если минимальное значение перебора не больше максимального
    else if (min <= max) {
        // приравниваем текущий элемент комбинации минимальному значению перебора
        combination[pos] = min;
        // делаем первый вызов рекурсии, увеличивая на 1, и минимальное значение перебора,
        // и индекс текущего элемента комбинации
        combineStep(combination, sz, min + 1, max, pos + 1, consumer);
        // когда закончатся все рекуррентные вызовы предыдущей команды;
        // Она перебрала все комбинации, у которых после элемента с
        // индексом `pos` нет значений, равных `min+1`; теперь
        // запускаем перебор комбинаций, у которых есть `min+1`
        combineStep(combination, sz, min + 1, max, pos, consumer);
    }
}

Теперь рассмотрим сам метод поиска паттернов перебором. Он является точкой входа и запускает рекуррентное порождение комбинаций, по каждой из построенных комбинаций вычисляется подматрица.

Для каждой такой матрицы осуществляется поиск изоморфной паттерну перестановки. Если она найдена, то для восстановления полной комбинации необходимо найти обратную перестановку и применить её к перебираемой комбинации:

/**
 * Поиск изоморфных подграфов полным перебором
 *
 * @param source       матрица-источник
 * @param sourceSize   размер стороны дата-графа
 * @param pattern      искомый паттерн
 * @param patternSize  размер стороны паттерна
 * @param hardCheck    флаг, нужна ли жёсткая проверка; если `hardCheck` равен `false`, то нулевому элементу паттерна
 *                     может соответствовать произвольное значение в переставленной подматрице, а если
 *                     `true`, то все элементы паттерна и переставленной подматрицы должны
 *                     совпадать с точностью до перестановки.
 * @return список таких комбинаций точек из источника, чтобы при составлении
 * соответствующих переставленных подматриц подграфы, построенные по ним,
 * были изоморфны заданному паттерну
 */
std::vector<CombinatoricsData>
getAllPatterns(int **source, int sourceSize, int **pattern, int patternSize, bool hardCheck) {
    // множество найденных паттернов
    std::vector<CombinatoricsData> res;

    // перебираем все возрастающие комбинации
    combine(sourceSize, patternSize, [&source, &patternSize, &res, &pattern, &hardCheck](const int *c) {
        // для каждой из них получаем матрицу из дата-графа по этой комбинации
        int **subMatrix = getSubMatrix(source, c, patternSize);

        // находим все перестановки, которые связывают паттерн
        // и составленную подматрицу
        std::unordered_set<CombinatoricsData, CombinatoricsData::HashFunction> ps =
                getAllIsomorphicPermutations(subMatrix, pattern, patternSize, hardCheck);

        // для каждой найденной перестановки
        for (CombinatoricsData p: ps) {
            // в множество добавляем переставленную комбинацию
            // в соответствии с той, которая найдена при поиске изоморфных
            // матриц
            res.emplace_back(
                    makePermute(c, patternSize, getReversePermutation(p.getData(), p.getSize())),
                    p.getSize()
            );
        }
    });

    // возвращаем множество найденных паттернов
    return res;
}

Проверим алгоритм поиска паттернов:

#include <vector>
#include "misc/combinatorics.h"
#include "patternResolver.h"

int main() {
    // матрица смежности дата-графа
    int sourceMatrix[7][7]{
            {0, 0, 0, 0, 1, 0, 0},
            {1, 0, 0, 0, 0, 0, 0},
            {0, 1, 0, 1, 0, 0, 0},
            {0, 1, 0, 0, 1, 0, 1},
            {0, 1, 0, 0, 0, 1, 0},
            {0, 0, 0, 1, 0, 0, 1},
            {0, 0, 1, 0, 0, 0, 0},
    };

    // подготавливаем матрицу
    int **source = new int *[7];
    for (int i = 0; i < 7; i++) {
        source[i] = new int[7];
        for (int j = 0; j < 7; j++)
            source[i][j] = sourceMatrix[i][j];
    }
    // матрица смежности паттерна
    int patternMatrix[3][3]{
            {0, 0, 1},
            {1, 0, 0},
            {0, 1, 0}
    };
    // подготавливаем матрицу
    int **pattern = new int *[3];
    for (int i = 0; i < 3; i++) {
        pattern[i] = new int[3];
        for (int j = 0; j < 3; j++)
            pattern[i][j] = patternMatrix[i][j];
    }

    // ищем изоморфные комбинации
    std::vector<CombinatoricsData> cds =
            getAllPatterns(source, 7,pattern,3, true);

    // выводим построчно найденные комбинации
    for (CombinatoricsData cd: cds) {
        for (int k = 0; k < cd.getSize(); k++)
            std::cout << cd.getData()[k] << " ";
        std::cout << std::endl;
    }

    return 0;
}

На консоль будет выведено:

Быстрый поиск паттернов​

Для быстрого поиска будем порождать все неупорядоченные комбинации длины, равной количеству вершин в паттерне. Если мы перебираем все комбинации, а не только упорядоченные, то нам не нужно дополнительно искать изоморфные перестановки. Связь между вершинами подграфа из дата-гарфа и паттернов определяется однозначно.

При этом каждое новое значение комбинации на новом шаге рекурсии будет дополнять матрицу смежности того или иного подграфа одним столбцом и одной строкой. Если перед вызовом рекурсии проверять только эти новые элементы, то на следующем шаге их учитывать уже не нужно, достаточно проверить новую строку и новый столбец.

Если они совпали с соответствующими строкой и столбцом паттерна, то запускается новый шаг рекурсии для следующего значения комбинации. Если равенство элементов нарушается, то эта ветвь рекурсии не порождает новых вызовов.

Рассмотрим паттерн 3×3 (с вершинами ABC):

Возьмём три комбинации [0, 2, 4], [0, 3, 1], и [5, 6, 4], перенесём их на матрицу 7×7

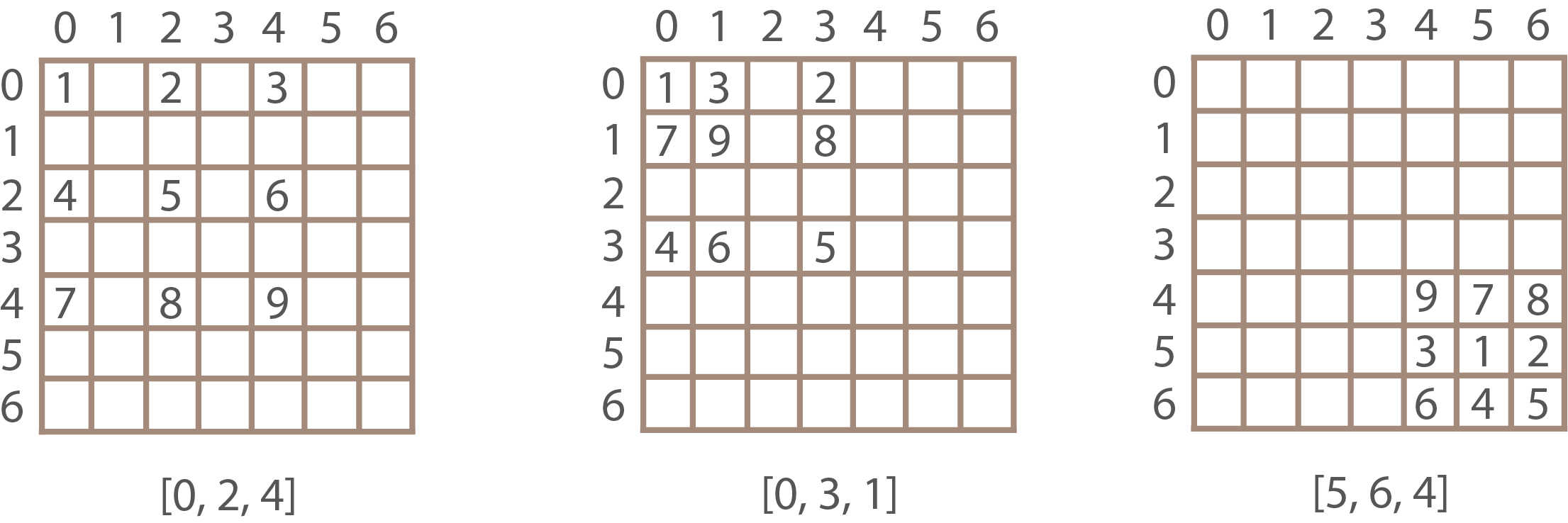
Совместим три полученных матрицы и заполним оставшиеся элементы случайными значениями:

Найдём с помощью быстрого алгоритма все изоморфные комбинации.

На первом шаге связывается первая вершина паттерна ABC:

Из всех рассмотренных вершин в качестве первой дата-графа подходят только: [0, ...] и [5, ...]

Каждая из таких удачных вершин породит рекуррентный вызов для определения комбинаций, длины 2:

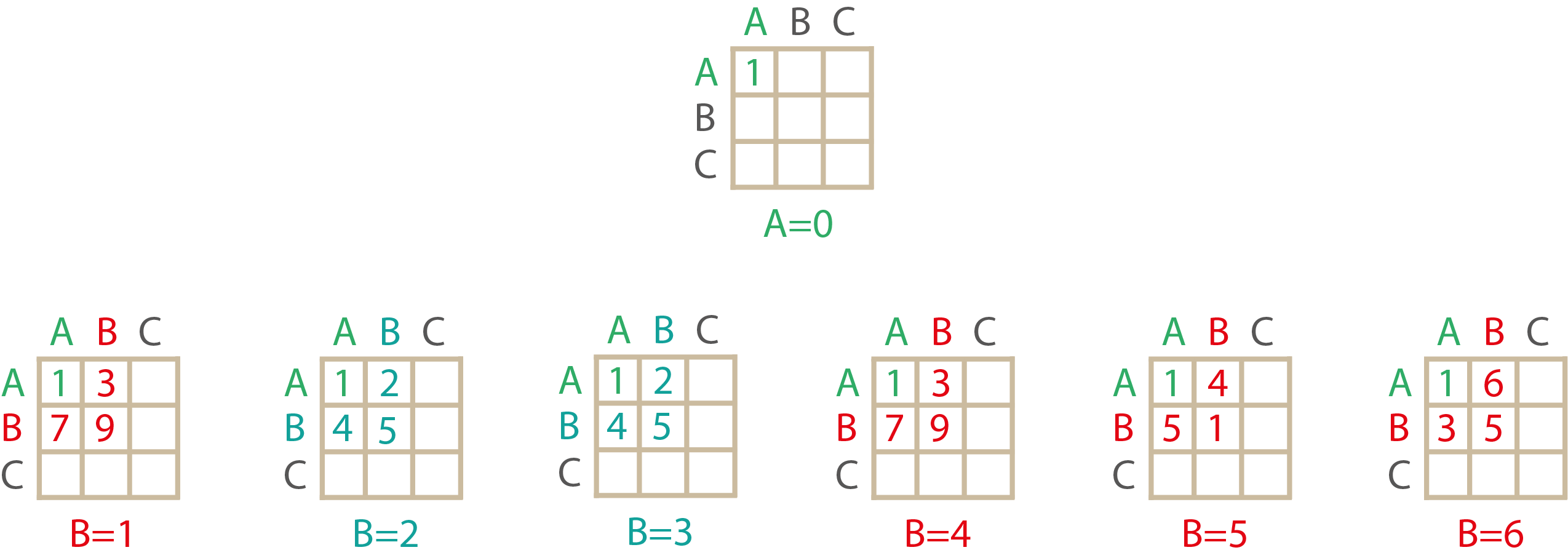
На основе комбинации [0, ...] могут быть построены комбинации [0, 2, ...] и [0, 3, ...]

Рассмотрим первую из них:

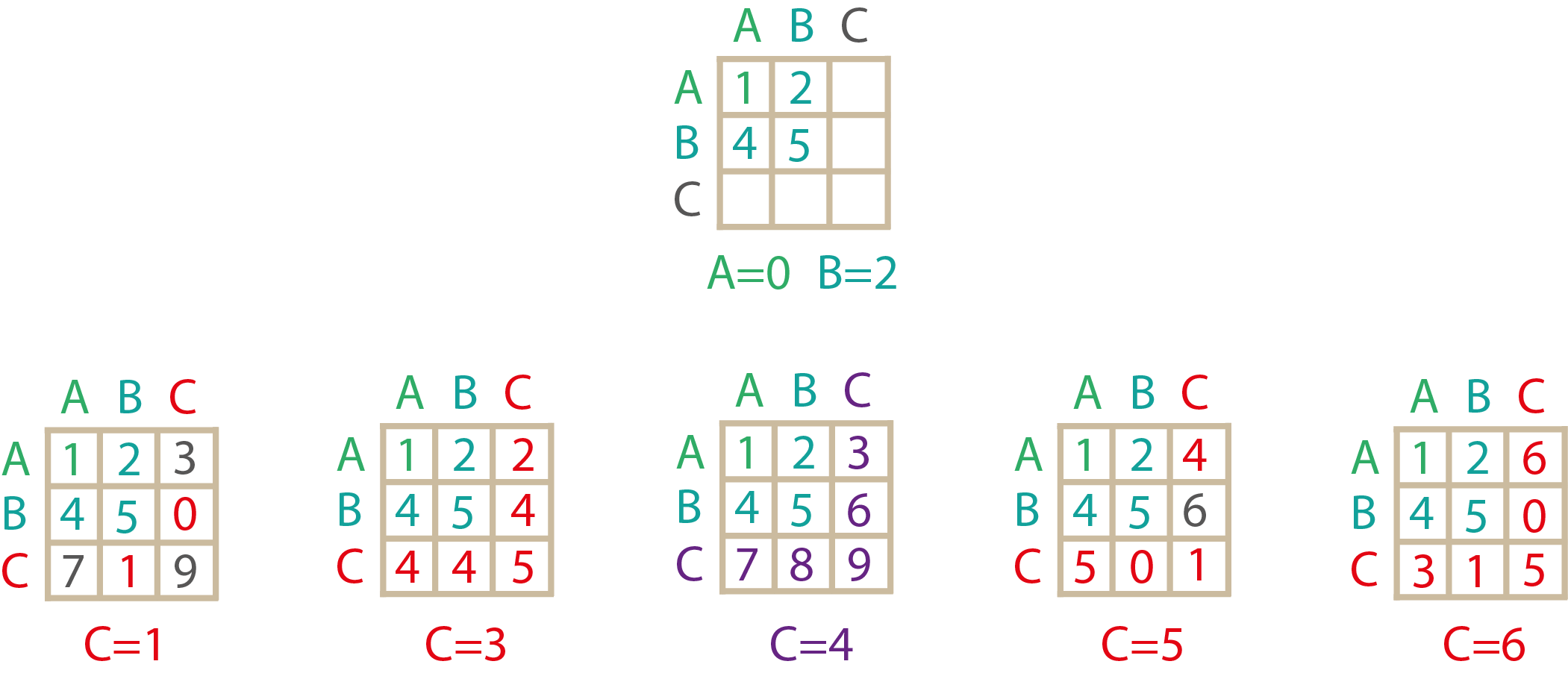
На её основе можно построить только комбинацию [0, 2, 4]

Вторая комбинация [0, 3, ...] даст всего один вызов:

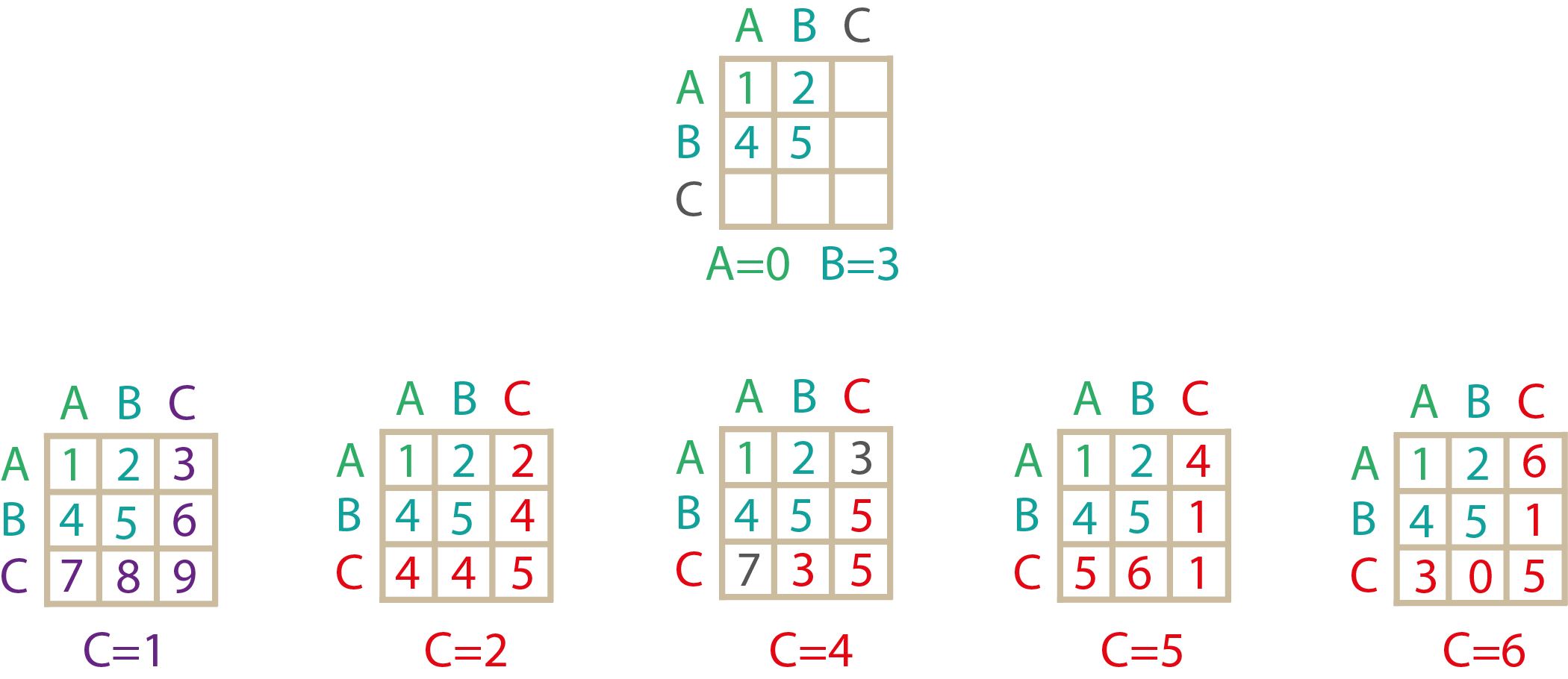
В итоге получится всего одна комбинация [0, 3, 1]

Вернёмся к комбинации [5, ...]:

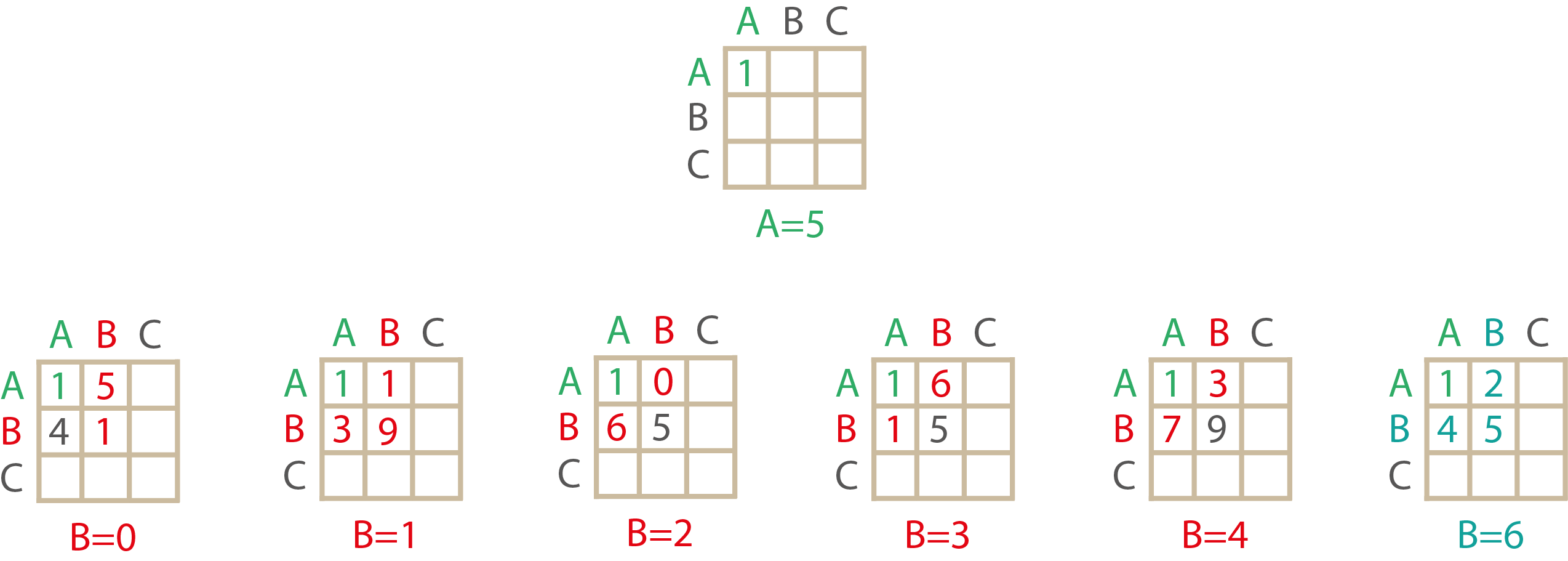
На её основе может быть построена только одна комбинация [5, 6, ...]

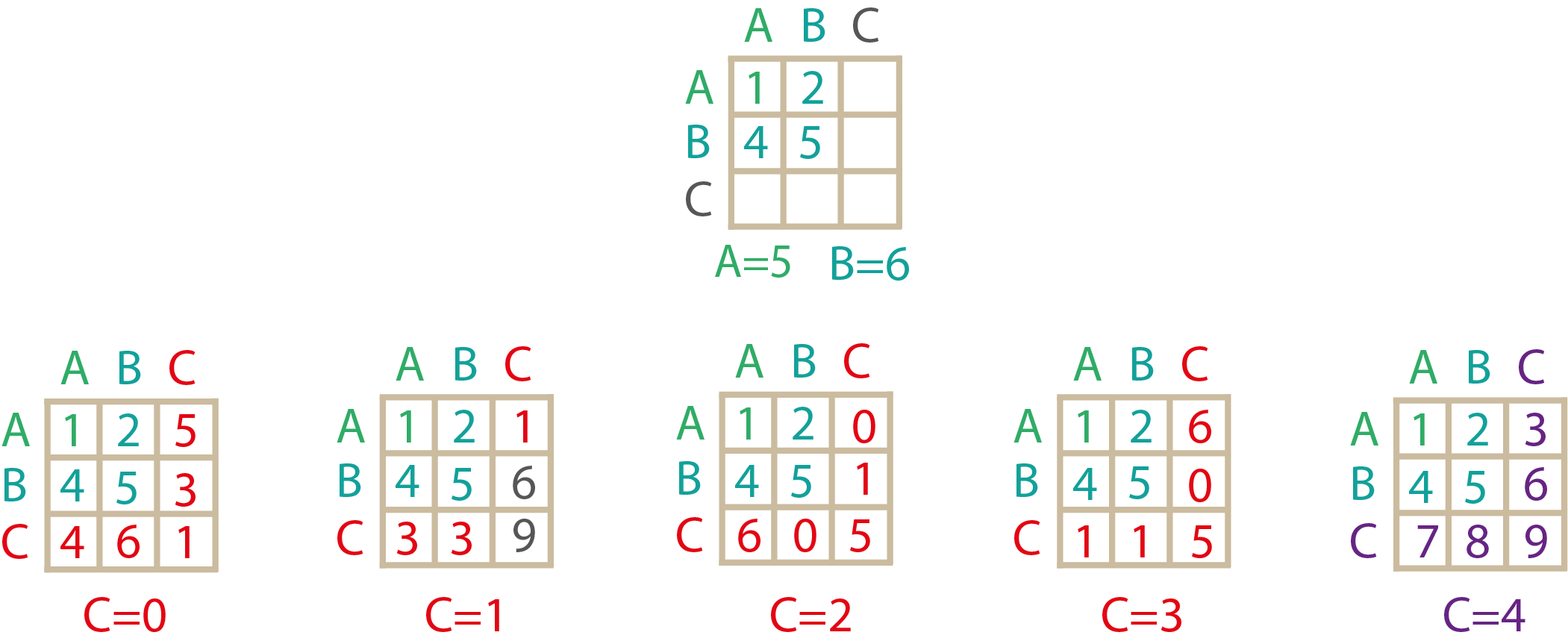
В свою очередь из неё получится только комбинация [5, 6, 4]

Исходный код​

Ниже представлен код быстрого поиска изоморфных подграфов. Точка входа:

std::vector<CombinatoricsData>
fastGetAllPatterns(int **source, int sourceSize, int **pattern, int patternSize, bool hardCheck) {

Полный код:

/**
 * Проверить совпадение самого правого столбца
 * и самой нижней строки подматрицы дата-графа,
 * полученной по соответствующей комбинации
 * (проверяются только новые элементы,
 * они находятся в самом нижнем ряду и в самой правой колонке)
 *
 * @param source      дата-граф
 * @param pattern     паттерн
 * @param combination комбинация
 * @param cnt         кол-во элементов в комбинации
 * @param hardCheck   флаг, нужна ли жёсткая проверка
 * @return флаг, совпадают ли матрицы по углу
 */
bool checkMatrixEdge(
        int **source, int **pattern, const int *combination, int cnt, bool hardCheck
) {
    // перебираем элементы самого нижнего ряда матрицы
    // и самой правой колонки
    for (int i = 0; i < cnt; i++) {
        // если жёсткая проверка
        if (hardCheck) {
            // если элемент из паттерна в правом столбце не совпадает с соответствующим
            // элементом из дата-графа
            if (pattern[i][cnt - 1] != source[combination[i]][combination[cnt - 1]])
                // возвращаем флаг, что матрицы не равны по уголку
                return false;
            // если элемент из паттерна в нижней строке не совпадает с соответствующим
            // элементом из дата-графа
            if (pattern[cnt - 1][i] != source[combination[cnt - 1]][combination[i]])
                // возвращаем флаг, что матрицы не равны по уголку
                return false;
        } else { // если нежёсткая проверка
            // если элемент из паттерна в правом столбце ненулевой и не совпадает с соответствующим
            // элементом из дата-графа
            if (pattern[i][cnt - 1] != 0 && pattern[i][cnt - 1] != source[combination[i]][combination[cnt - 1]])
                // возвращаем флаг, что матрицы не равны по уголку
                return false;
            // если элемент из паттерна в нижней строке ненулевой и не совпадает с соответствующим
            // элементом из дата-графа
            if (pattern[cnt - 1][i] != 0 && pattern[cnt - 1][i] != source[combination[cnt - 1]][combination[i]])
                // возвращаем флаг, что матрицы не равны по уголку
                return false;
        }
    }

    // если не встречено неравных элементов, то возвращаем флаг, что матрицы равны по уголку
    return true;
}


/**
 * Шаг поиска паттерна
 *
 * @param consumer      обработчик найденной комбинации
 * @param used          массив флагов, использовалась ли уже i-я точка
 * @param source        дата-граф
 * @param sourceSize    размер стороны дата-графа
 * @param pattern       искомый паттерн
 * @param patternSize   размер стороны искомого паттерна
 * @param sourcePowers  степени вершин источника
 * @param patternPowers степени вершин паттерна
 * @param cnt           кол-во обработанных элементов
 * @param combination   массив комбинации
 * @param hardCheck     флаг, нужна ли жёсткая проверка
 * @param consumer      лямбда выражение (int *c)->{}
 */
template<typename F>
void fastFindPatternStep(
        bool *used, int **source, int sourceSize, int **pattern,
        int patternSize,
        int *sourcePowers, int *patternPowers, int cnt, int *combination,
        bool hardCheck, const F &consumer
) {
    // если уже выбрана хотя бы одна точка для комбинации и при этом
    // матрица, составленная из дата-графа по этой комбинации,
    // не совпадает с соответствующей подматрицей паттерна
    // (нам нужно проверить только новые элементы,
    // они находятся в самом нижнем ряду и в самой правой колонке)
    if (cnt > 0 && !checkMatrixEdge(source, pattern, combination, cnt, hardCheck))
        return;

    // если получено нужное кол-во элементов комбинации,
    if (cnt == patternSize)
        // обрабатываем её
        consumer(combination);
    else
        // в противном случае перебираем все вершины графа
        for (int i = 0; i < sourceSize; i++) {
            // если i-я точка уже использована, или её степень меньше степени
            // следующей точки в паттерне
            if (used[i] || (hardCheck && sourcePowers[i] < patternPowers[cnt]))
                continue;

            // говорим, что i-я точка использована
            used[i] = true;
            // добавляем индекс точки в комбинацию
            combination[cnt] = i;

            // вызываем следующий шаг рекурсии
            fastFindPatternStep(
                    used, source, sourceSize, pattern, patternSize, sourcePowers,
                    patternPowers, cnt + 1, combination, hardCheck, consumer
            );

            // возвращаем значение флага
            used[i] = false;
        }
}


/**
 * Быстрый поиск изоморфных подграфов
 *
 * @param source        дата-граф
 * @param sourceSize    размер стороны дата-графа
 * @param pattern       искомый паттерн
 * @param patternSize   размер стороны паттерна
 * @param hardCheck     флаг, нужна ли жёсткая проверка; если `hardCheck` равен `false`, то нулевому элементу паттерна
 *                      может соответствовать произвольное значение в переставленной подматрице, а если
 *                      `true`, то все элементы паттерна и переставленной подматрицы должны
 *                      совпадать с точностью до перестановки.
 * @return список таких комбинаций точек из источника, чтобы при составлении
 * соответствующих переставленных подматриц, подграфы, построенные по ним,
 * были изоморфны заданному паттерну
 */
std::vector<CombinatoricsData>
fastGetAllPatterns(int **source, int sourceSize, int **pattern, int patternSize, bool hardCheck) {
    // множество найденных паттернов
    std::vector<CombinatoricsData> res;
    // флаги, использована ли уже та или иная точка
    bool *used = new bool[sourceSize];
    for (int i = 0; i < sourceSize; i++)
        used[i] = false;
    // текущая комбинация
    int *combination = new int[patternSize];
    // степени вершин в дата-графе
    int *sourcePowers = getPowers(source, sourceSize);
    // степени вершин в паттерне
    int *patternPowers = getPowers(pattern, patternSize);

    // запускаем рекурсию
    fastFindPatternStep(
            used, source, sourceSize, pattern, patternSize,
            sourcePowers, patternPowers, 0, combination, hardCheck, [&res, &patternSize](int *c) {
                res.emplace_back(CombinatoricsData(c, patternSize));
            }
    );

    // возвращаем множество найденных паттернов
    return res;
}

Проверим этот код на примере из предыдущего блока:

#include <vector>
#include "misc/CombinatoricsData.h"
#include "fastPatternResolver.h"

int main() {
    // паттерн
    int patternMatrix[3][3] = {
            {1, 2, 3},
            {4, 5, 6},
            {7, 8, 9}
    };
    int **pattern = new int *[3];
    for (int i = 0; i < 3; i++) {
        pattern[i] = new int[3];
        for (int j = 0; j < 3; j++)
            pattern[i][j] = patternMatrix[i][j];
    }

    // матрица смежности дата-графа
    int sourceMatrix[7][7]{
            {1, 3, 2, 2, 3, 4, 6},
            {7, 9, 1, 8, 0, 3, 3},
            {4, 0, 5, 4, 6, 6, 0},
            {4, 6, 4, 5, 5, 1, 1},
            {7, 2, 8, 3, 9, 7, 8},
            {5, 1, 0, 6, 3, 1, 2},
            {3, 6, 1, 0, 6, 4, 5}
    };
    int **source = new int *[7];
    for (int i = 0; i < 7; i++) {
        source[i] = new int[7];
        for (int j = 0; j < 7; j++)
            source[i][j] = sourceMatrix[i][j];
    }


    // получаем список найденных комбинаций
    std::vector<CombinatoricsData> fastPatterns = fastGetAllPatterns(source, 7, pattern, 3, true);
    // для каждой комбинации выводим её элементы
    for (CombinatoricsData cd: fastPatterns) {
        for (int i = 0; i < 3; i++)
            std::cout << cd.getData()[i] << " ";
        std::cout << std::endl;
    }

    return 0;
}

На консоль будет выведено:

Найдены те же перестановки

Статистика​

Для сравнения алгоритма поиска паттернов перебором и алгоритма быстрого поиска было проведено несколько тестов. Их результаты были упорядочены по затраченному времени на поиск перебором.

Оба теста выполнялись для случайных матриц смежности дата-графа и паттерна. Перед поиском паттернов в дата-граф добавлялось несколько переставленных случайным образом подграфов (заменялись соответствующие элементы), после чего засекалось время поиска всех паттернов перебором и быстрым алгоритмом.

На графиках по оси OX отложен индекс элемента в упорядоченном списке результатов тестов, по оси OY - затраченное на соответствующий тест время в микросекундах.

Первый график показывает время в мкс, затраченное на поиск паттернов с количеством вершин от 4 до 5 включительно в дата-графе с количеством вершин от 6 до 7 включительно:

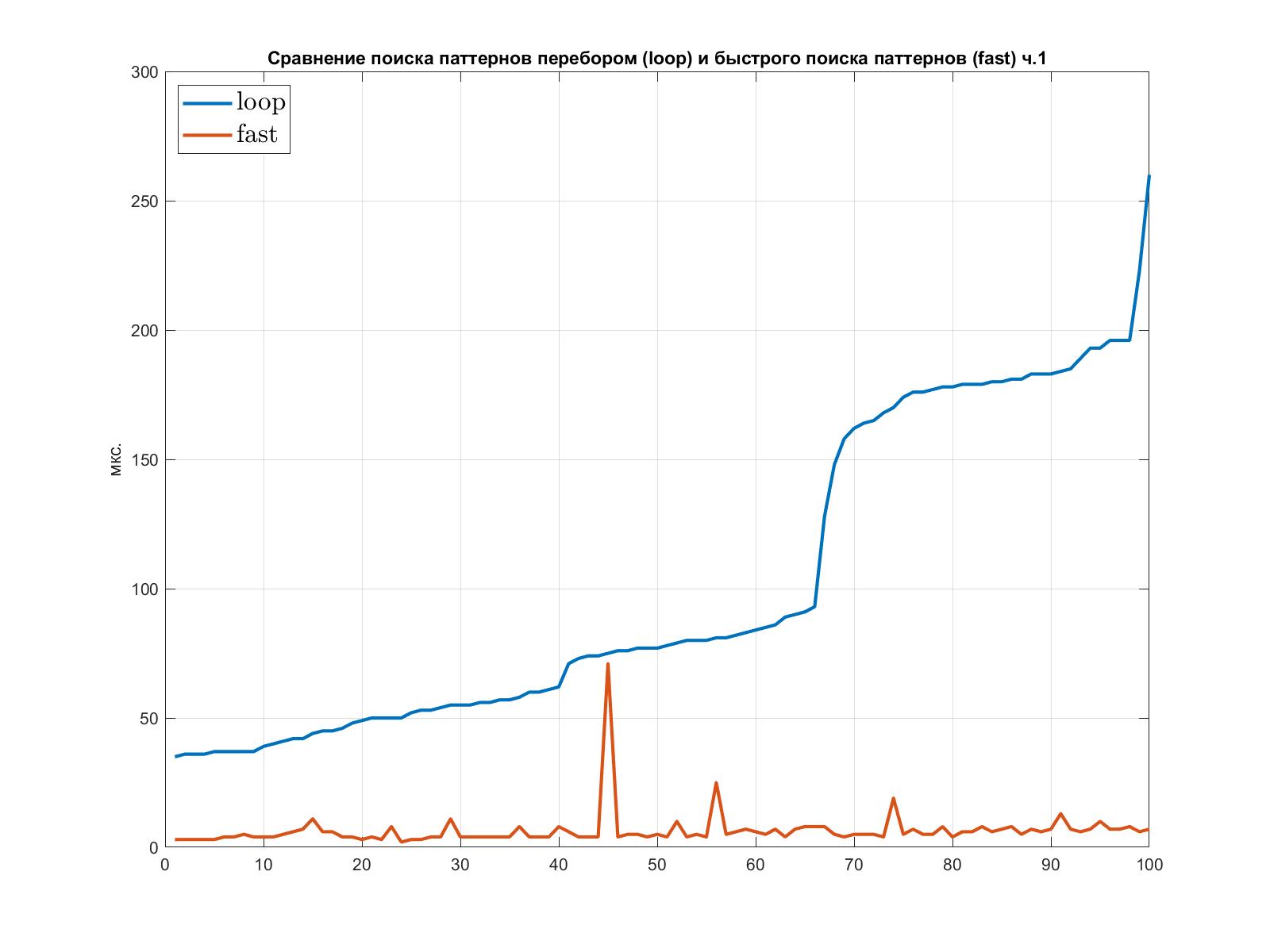
Второй график показывает время в мкс, затраченное на поиск паттернов с количеством вершин от 6 до 7 включительно в дата-графе с количеством вершин от 9 до 11 включительно:

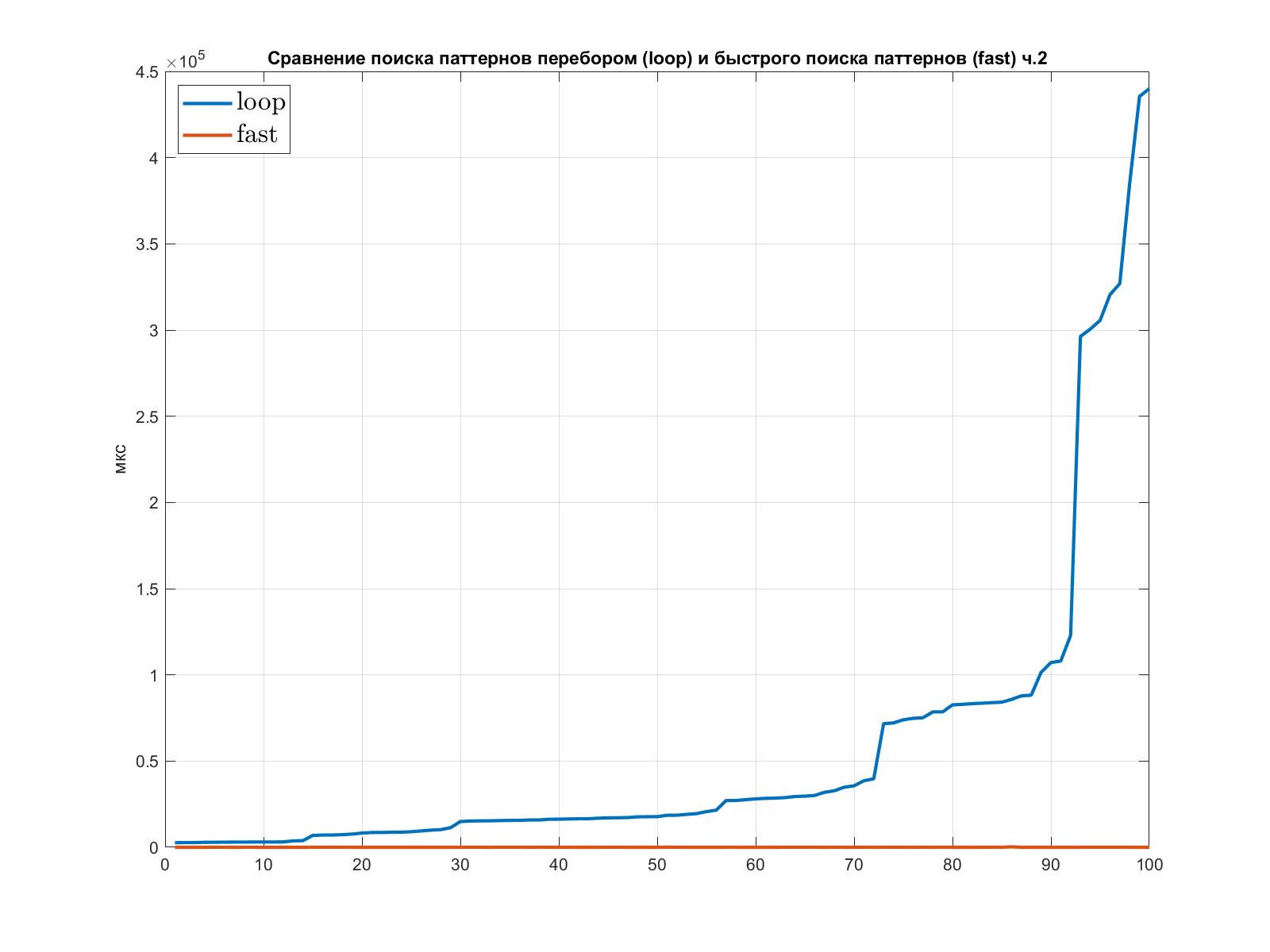
Спасибо за внимание.