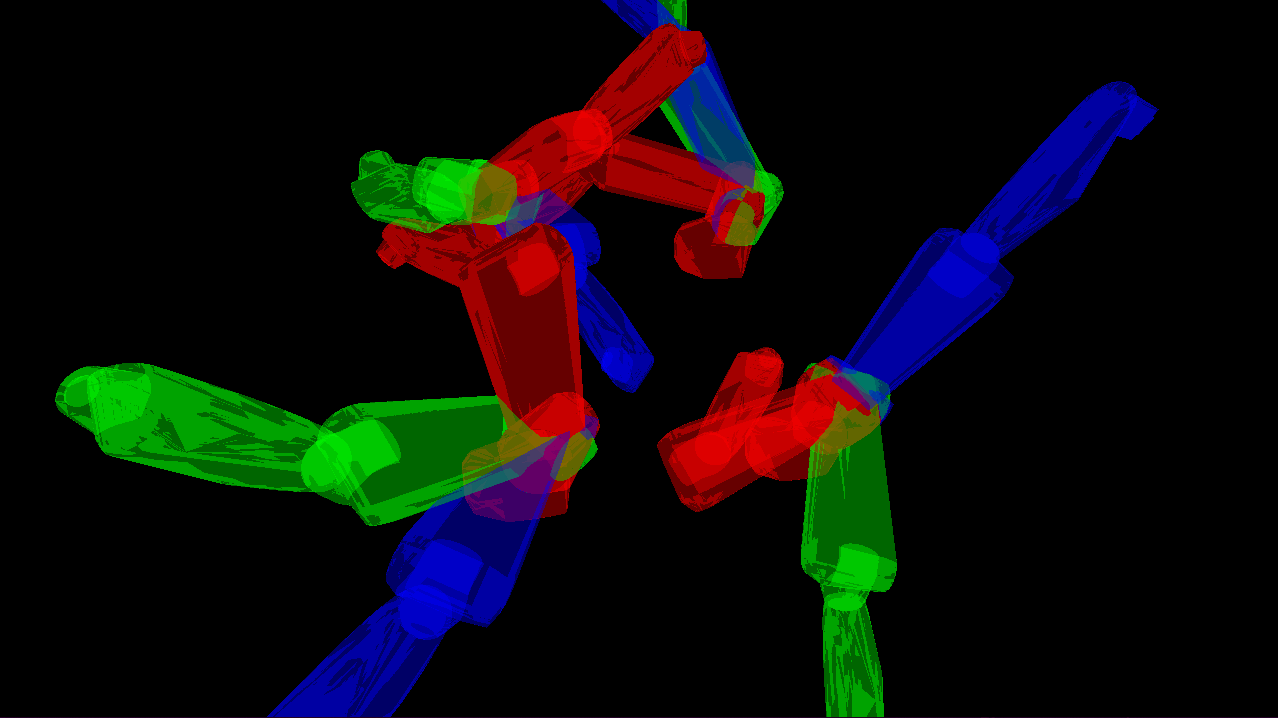
Привет, Хабр!
В данной статье сделан обзор на OpenSource фреймворк планирования движения BMPF.
На данный момент подавляющее большинство средств планирования движения работает по одному и тому же принципу: вся сцена описывается как один робот, после чего выполняется планирование на сетке (чаще всего A*, подробнее можно прочитать здесь).
У такого подхода есть две основных проблемы:
планирование на сетке гарантирует допустимость только состояний в её узлах, промежуточные никак не оцениваются и не проверяются
для сцены из нескольких роботов размерность пространства планирования получается слишком большой (алгоритмическая сложность планирования растёт как показательная функция).
Данный фреймворк решает обе озвученные проблемы. С документацией фреймворка можно ознакомиться здесь.
Архитектура фреймворка
Обычно для планирования движения использую ROS+MoveIt. Однако развёртывание этого окружения требует времени, а необходимость использования ROS качественно повышает порог вхождения.
MoveIt работает с URDF-файлами и всегда воспринимает сцену как единого робота.
Общая идея фреймворка BMPF заключается в двухэтапном планировании пути:
поиск "некрасивого" пути
оптимизация
Поиск некрасивого пути позволяет быстрее дойти до цели. Например, можно всегда смещаться только вдоль одной из координат. Такой путь можно потом оптимизировать: т.е. подобрать похожий, но с нужными требованиями. Имея готовый путь в многомерном пространстве, алгоритмически дешевле построить "некрасивый" путь, а потом менять его, чем строить новый красивый.
Поэтому в данном фреймворке всё окружение написано "с нуля". Для проверки коллизий используется библиотека solid3.
Для описания системы роботов разработан довольно простой формат *.murdf.
Пример файла описания сцены:
{
"robots" : [
{
"model" : "../../config/urdf/kuka_six.urdf",
"pos" : [ 0, 0, 0 ],
"rpy" : [ 0, 0, 0 ],
"scale" : [ 1, 1, 1 ]
},
{
"model" : "../../config/urdf/tetris_4.urdf",
"pos" : [ 0, 0, 0.85 ],
"rpy" : [ 0, 0, 0 ],
"scale" : [ 1, 1, 1 ]
},
{
"model" : "../../config/urdf/sphere.urdf",
"pos" : [ 1.03, 0.450, 0.64 ],
"rpy" : [ 0, 0, 0 ],
"scale" : [ 2.03, 1, 1 ]
}
],
"name" : "saved scene"
}Он является надстройкой над json. Для каждого робота указывается путь к его описанию, а также три вектора, описывающие его преобразование в пространстве:
смещение: x, y, z
углы поворота: крен (roll), тангаж (pitch), рыскание (yaw)
коэффициенты масштабирования вдоль осей:
Редактор сцены
Для работы со сценой написано графическое приложение
bmpf_scene_editor
Поиск пути
Суть планирования на сетке заключается в том, что каждой вещественной координате состояния мы ставим в соответствие целочисленную координату из заданного диапазона.
Получается, что в данном планировщике одно и то же пространство конфигураций описывается двумя пространствами: вещественным пространством состояний и целочисленным пространством координат. При этом размерности пространств совпадают.
Поиск пути осущетсвляется за счёт перемещения по сетке планирования. Когда путь на сетке найден, каждой его точке сопоставляется состояние робота, и на их основе строится путь.
Часть планировщиков работает с использованием нод. Нодами называются записи об обработанных точках на сетке планирования и некоторая вспомогательная информация. В данном фреймворке у нод хранится метрика расстояния от стартовой точки до рассматриваемой.
Суть алгоритма планирования с использованием нод сводится к взятию самой удачной ноды из списка на обработку, её обработке и добавлению в список всех её ещё не рассмотренных соседей. Этот список называется открытым множеством.
Чтобы хранить все обработанные точки в закрытом множестве, используется множество на хэшах, при этом в качестве исходного значения хранится свёртка координат
/**
* свернуть координаты coords в скаляр (size - размер СК)
* @param coords координаты
* @param size размер вдоль каждой оси
* @return свёртка
*/
unsigned long bmpf::convState(std::vector<int> &coords, int size) {
unsigned long code = 0;
int m = 1;
for (int coord: coords) {
code += m * coord;
m *= size;
}
return code;
}Такой алгоритм гарантирует биективное (один к одному) отображение множества координат и множества свёрток, поэтому вместо высчитывания хэша от объекта ноды высчитывается хэш от свёртки
/**
* поиск координат в списке закрытых нод
* @param coords координаты
* @return флаг, содержатся ли координаты в закрытом списке
*/
bool NodeGridPathFinder::_findCoordsInClosedList(std::vector<int> &coords) {
long code = (long) convState(coords, _gridSize);
return _closedStateConvCodeSet.find(code) != _closedStateConvCodeSet.end();
}Многомерные пространства
Если такой алгоритм применить для сцены с несколькими роботами, то размерность пространства возрастает пропорционально. Это означает, что количество соседей c_n растёт как степенная функция:
где n - суммарное количество звеньев.
При n = 6 размер списка будет равен 728728, а при n = 24 (сцена из четырёх роботов) уже 282429536480≈3×10^{11}.
Такая скорость количества проверок на каждом этапе приводит к необходимости планировать пути на вычислительных кластерах.
Поэтому в основе данного фреймворка лежит идея двухэтапного поиска пути. Первый этап быстро находит "плохой" путь, не перебирая часть соседей, а на втором этапе выполняется оптимизация уже найденного пути.
Единичные смещения
Самым простым решением является обработка только тех соседей, у которых изменяется ровно одна координата. Такие смещения будем называть единичными. Тогда размер списка смещений с ростом размерности будет расти пропорционально n, а не экспоненциально и равен 2n. Этот подход пропускает случаи, когда только изменение двух или более координат сразу даст возможность построить маршрут.
Хотя такие ситуации крайне редки и чаще всего решаются повышением дискретности сетки планирования, данная проблема решается в глобальных планировщиках, о которых будет рассказано ниже.
Упорядоченные смещения
В ситуациях, когда у стартовой и конечной конфигураций значительно отличаются разности по координатам (например, только две отличаются сильно, а остальные - незначительно), то при обычной метрике лучше упорядочить смещения.
Например, если на сцене присутствует четыре робота, и первые три робота пришли в заданную точку, а четвёртый ещё нет, то алгоритм начинает рассматривать не только смещения, меняющие положение нужного робота, но и тех, которые уже находятся в правильном положении.
Если бы открытое множество могло иметь бесконечный размер, то такой проблемы не существовало бы, но у нас оно ограничено.
Т. к. алгоритм добавляет новых соседей в открытое множество, и удаляет старых, то порядок смещений становится важным.
Это можно исправить, упорядочив список смещений: для одного робота, необходимо сначала смещаться вдоль тех измерений, которые имеют самые большие отклонения. Для системы роботов необходимо смещаться сначала вдоль измерений, которые соответствуют роботу, который ещё не пришёл к цели, а потом уже тех, которые пришли к цели.
MultiRobot
При планировании подавляющая часть пути не приводит к коллизиям, поэтому у данного планировщика планирование сначала выполняется для каждого робота независимо. Потом их пути совмещаются, и проверяются коллизии у объединённого пути. Участки, соответствующие коллизиям планируются заново, но уже для сцены из четырёх роботов.
Такую логику можно сравнить с оптимизаторами: локальные и глобальные. Локальные планировщики решают конкретную задачу планирования, а глобальные являются своего рода надпрограммами для локальных. Они используют их внутри себя и с их помощью обеспечивают те или иные требования к проложенному пути.
Непрерывный планировщик
Основная проблема всех планировщиков на сетке заключается в том, что такие алгоритмы дают гарантию отсутствия коллизий только в непосредственных узлах сетки. При этом промежуточные значения между опорными точками пути могут соответствовать коллизии.
Алгоритм работы непрерывного планировщика похож на multirobot, но при этом основным планировщиком является multirobot. При проверке определяются коллизии, но с промежуточными проверками каждого этапа пути.
Если все промежуточные положения тоже свободны от коллизий, то алгоритм идёт дальше, а если хотя бы одна точка соответствует коллизии, то две опорные точки назначаются коллизионными. Такой запас делается для того, чтобы планирование не выполнялось вблизи коллизий. Это опасно для технологического процесса, т. к. коллизионные модели всегда приближённые, а шаг сетки у локального планировщика сильно меньше, чем шаг глобального.
Т. к. глобальный планировщик направленный, то и найденные промежутки коллизии будут отличаться всего в нескольких координатах. В таких случаях как раз больше всего подходит упорядоченный планировщик.
Моделирование
Пример проложенных путей для одного робота
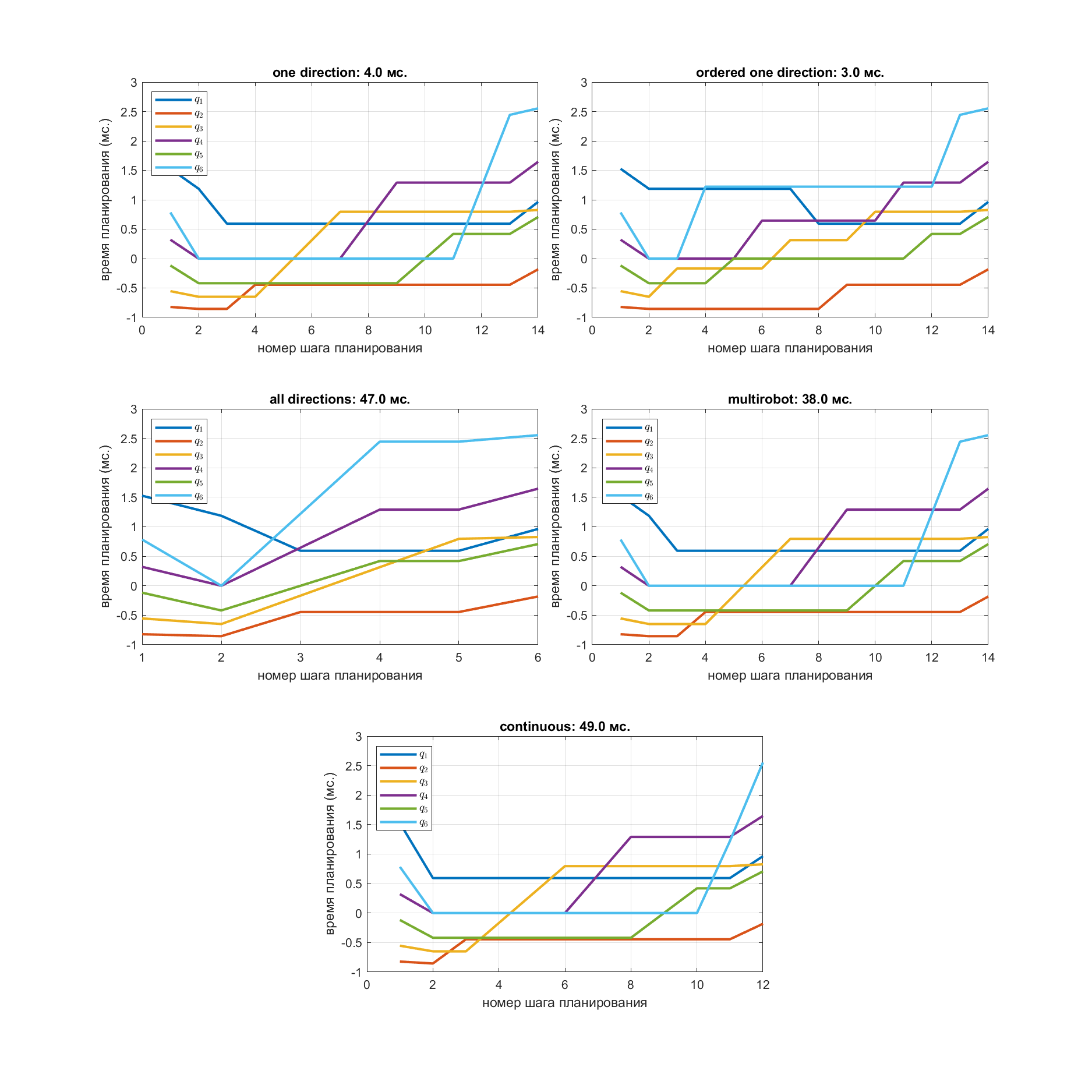
q_i - угол поворота i-го звена робота в радианахГрафик временных затрат при планировании

Четыре робота
В сравнении не участвует планировщик all-direction, т. к. для четырёх роботов планирование этим алгоритмом требует слишком много времени.
Проложенные пути для планировщиков, не учитывающих непрерывность

q_i - угол поворота i-го звена робота в радианахСравнение планирования multirobot и непрерывного планирования
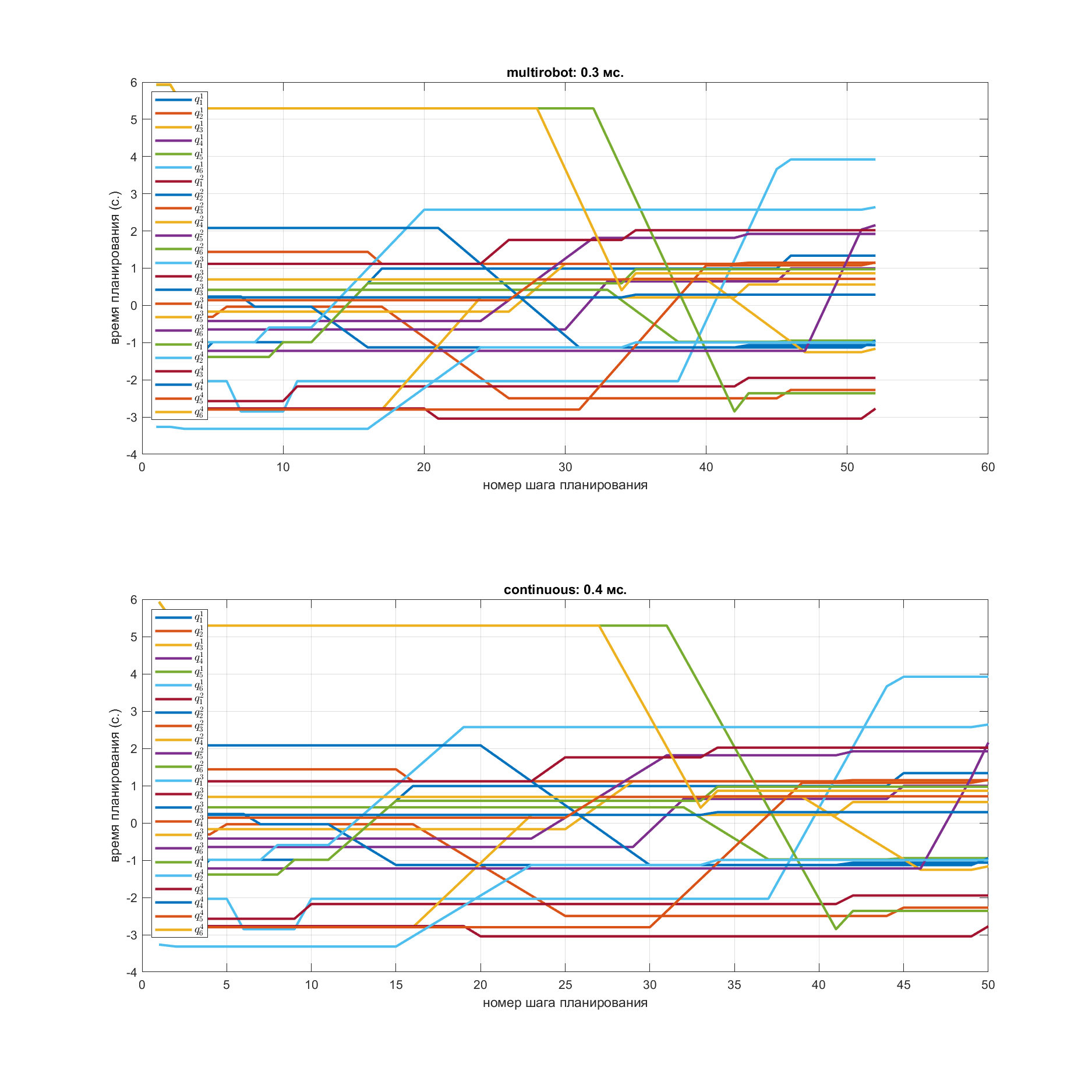
q_i - угол поворота i-го звена роботов в радианахТ. к. в этих экспериментах время работы непрерывного планировщика и multirobot почти совпадают, то первый исключён из рассмотрения

Сравнение скорости работы multirobot и направленного планировщика (двух самых быстрых)

Визуализация путей
Для визуализации путей написано приложение bmpf_render_single_path. Оно показывает конкретный путь из json-файла

Оптимизация пути
Построив маршрут с помощью того или иного планировщика, необходимо оптимизировать этот маршрут.
Пока что в данном фреймворке реализована только медианная оптимизация. По аналогии с медианным фильтром алгоритм последовательно перебирает тройки точек маршрута и заменяет координаты средней из них на среднее арифметическое крайних точек, если новое состояние не соответствует коллизии.
Т. к. путь должен быть непрерывным, то при проверке новой точки необходимо проверить, что не только сама точка не соответствует коллизии, но и путь от соседних опорных точек непрерывен. Такую оптимизацию будем называть непрерывной.
Для повышения гладкости можно дополнительно разделить каждый этап исходного пути на заданное количество частей.
Для сравнения работы алгоритма было проведено несколько непрерывных оптимизаций одного и того же пути.

q_i - угол поворота i-го звена робота в радианахМонотонные траектории
Когда построен путь, необходимо составить зависимость состояния робота от времени. Такую зависимость называют траекториями.
Классический способ построения траекторий предполагает использование сплайнов. Каждой точке пути сопоставляется временная метка, в какой момент робот должен прийти в ту или иную точку пути.
С каждым этапом пути сопоставляется полином заданной степени так, чтобы в каждой точке значение полинома следующего промежутка и полинома предыдущего совпали.
При планировании обычными сплайнами возникает проблемы перерегулирования (overshooting). В таких случаях робот попадает в опорные точки траектории в заданное время, но в промежуточных положениях углы поворота могут выйти за границы допустимых значений. Это приведёт к аварийной остановке робота.
Чтобы гарантировать отсутствие перерегулирования, необходимо строить монотонные траектории. Самый популярный алгоритм построения монотонных траекторий разработан Фритчем и Карлсоном. Подробнее о нём можно прочитать здесь.
Планировщик траекторий использует базовые полиномы Эрмита, корректируя скорости в каждой точке так, чтобы итоговый полином был монотонным. (Скорости в начале задаются с помощью трёхточечной разности)
Для каждой координаты создаётся свой монотонный интерполятор, а после в любой момент времени по временной метке из интерполятора получаем соответствующее состояние.
Также в классе реализована возможность получать по времени скорости и ускорения. Помимо самих значений координат, каждая точка траектории снабжается временной меткой, которая записывается в начале вектора состояния.
Сеть
Для работы с фреймворком без компиляции написан ряд демонстрационных серверов и клиентов.

Исходники клиентов дополнительно лежат в отдельном репозитории.
Сам базовый сервер работает в следующей логике: в бесконечном цикле с заданной задержкой сервер ожидает подключения клиента. Как только клиент подключен, запускается новый цикл обработки запросов.
Т. к. запрос может быть достаточно длинным, то его данные разобьются на несколько посылок. Поэтому все команды оборачиваются символом *. Данные внутри задаются с помощью json.
Каждая из команд состоит из кода команды и данных:
{
"command": 0,
"data": {
...
}
}Спасибо за внимание.


Dynasaur
А из питона не предполагается работать?
aok-buran Автор
Фреймворк собирается в набор серверов в deb-пакете, поэтому можно переписать клиенты под питон. В будущем планирую добавить клиенты и на python, и на java.
Собрать полноценный аналог библиотеки под питон я до Вашего вопроса не думал, но идея, на мой взгляд, хорошая. Добавлю в тасклист.