Задача не сложная, явно не уровня всероссийской школьной олимпиады. Однако её решение требует перебора нескольких десятков вариантов, что даёт возможность ошибиться. Может быть, имеется и более красивое решение, не требующее внимательности и аккуратности, но автор его не нашёл. Эту столь удобную задачу принёс @makondo, за что ему большое спасибо!
Для решения будем использовать Visual Studio Code с расширениями, обеспечивающими интерфейс Jupyter Notebook, использующий интерпретатор F#. Весь код в настоящей статье можно выполнить и в интерпретаторе F#, который входит в состав дистрибутива Visual Studio.
Постановка задачи
Итак, сама задача: найти количество значений, которые на промежутке [0; 1) принимает функция
Промежуток [0; 1) – множество всех чисел, которые меньше 1 и не больше 0. Квадратными скобками обозначается операция взятия целой части числа. Например, [5.5] = 5.
Подготовка к решению
Исследование функции f
Данная функция, как видно из её формулы, представляет собой сумму девяти функций, которые выдают неотрицательные целые числа
где
Каждая из этих функций кусочно-постоянная и неубывающая. Её график представляет собою лесенку со ступеньками равной длины. Чем больше k, тем ступеньки у лесенки короче. Для k = 2 на промежутке [0;1) оказываются всего две ступеньки: первая от 0 до половины, а вторая от половины до 1. Поэтому и сама функция f также является неубывающей, кусочно-постоянной и выдаёт только целые числа.
Для x < 0.1 все эти функции выдают 0. При x = 1 функция f выдаст сумму целых чисел от 2 до 10. Эта сумма равна 54. Целых чисел, которые больше или равны 0 и меньше или равны 54, существует 55 штук. Таким образом, ответ задачи не может быть больше, чем 55. Несложно доказать, что у каждой из девяти функций при x = 1 начинается очередная ступенька. x = 1 не входит в промежуток, для которого нужно найти кол-во значений, поэтому можно уменьшить верхнюю границу до 54.
Реализация функции f
Для порядка реализуем на F# саму функцию f . На самом деле мы не знаем, надо ли это для решения задачи. Скорее всего, пригодится, хотя бы для тестирования.
Создадим для начала коллекцию из целых чисел от 2 до 10, которые фигурируют в формуле. Пусть это будет список:
let ks = [ 2 .. 10 ]Вроде как ks мы завели на всякий случай, но теперь, когда есть именованная коллекция этих k, естественно её использовать для реализации нашей функции и последующих решений задачи:
let f x = List.sumBy ( float >> ( * ) x >> int ) ksИли в менее лаконичном варианте
let f x =
let fk k = int ( float k * x )
List.sumBy fk ksРазъяснения по синтаксису
Сначала рассмотрим второй, нелаконичный, вариант. Ключевое слово let служит также для заведения величин, которые являются функциями (да, в F# функции также принято называть величинами).
В заголовке функции после слова let указывается имя заводимой функции, а затем через пробелы (без скобок и запятых!) имена её параметров. Знак = служит для отделения заголовка и тела функции друг от друга.
Тело функции представляет собой одно выражение или блок кода, состоящий из выражений и заведений других величин, в т. ч. функций. Их нужно записывать с одинаковым отступом по отношению к заголовку. Функция выдаёт значение, вычисленное в последнем выражении в своём теле. (Поэтому тело функции не может завершаться заведением величины, т. к. область видимости имён всех заведённых в теле функции величин этим телом и ограничивается.)
Тело функции f состоит из двух строк. В первой строке заводится вспомогательная функция fk, а вторая представляет собой выражение, результат которого и будет возвращаемым значением функции.
let fk k = int ( float k * x )Функция fk имеет один параметр k. В своём теле она выполняет следующие действия:
преобразует свой параметр к типу float при помощи функции-оператора float;
умножает на x (поэтому интерпретатор определит, что у функции f параметр x должен иметь тип float);
округляет результат умножения до наименьшего целого и преобразует к типу int при помощи функции-оператора int.
В F# имеется целых 7 операторов применения (или – как принято говорить про процедурные языки – вызова) функции. Для основного из них не придумали лексему, компилятор его распознаёт, когда, разбирая выражение, обнаруживает, например, две величины (или подвыражения) подряд, т. е. не соединённые каким-либо оператором. Таким образом, a b означает применить величину а к величине b, при этом величина a должна являться функцией. Все операторы применения ассоциативны слева, это означает, что выражение a b c интерпретируется как (a b) c, но не как a (b c). Основной оператор применения имеет очень большой приоритет, поэтому параметр функции int пришлось заключить в скобки.
Вторая строка
List.sumBy fk ksприменяет функцию sumBy модуля List к величине fk и нашему списку чисел ks. Данный модуль входит в состав стандартных библиотек F# и распространяется вместе с компилятором и интерпретатором.
Функция List.sumBy применяет свой первый параметр к каждому элементу списка, а затем суммирует все полученные результаты применения.
Этот вариант плох тем, что в нём заводится именованная функция fk и это
имя используется лишь однажды. Автору статьи не удалось придумать более
подходящее имя, чтобы оно помогало понять код, а не запутывало.
В первом, лаконичном, варианте лишние именованные программные объекты отсутствуют. Вместо функции fk в нём используется выражение
float >> ( * ) x >> intОно представляет собою композицию из трёх функций, разделённых оператором композиции >> . Выражение a >> b означает сконструировать из величин a и b функцию, которая применяет к своему аргументу сначала функцию a, а потом к результату применяет функцию b.
Каждой функции в выражении float >> ( * ) x >> int соответствует одно из трёх действий тела fk, перечисленных выше. Следует иметь в виду, что такая композиция возможна лишь потому, что эти действия выполняются конвейерно, каждое получает на вход результат предыдущего (или аргумент функции fk) и передаёт свой результат следующему (или возвращает его из функции fk).
Скобки вокруг оператора умножения экранируют его грамматические свойства, результат вычисления выражения ( * ) обычная функция с двумя параметрами, к которым может быть применён оператор умножения. Это означает, что вместо a * b можно написать ( * ) a b.
Затем ( * ) применяется к x, в результате конструируется функция уже от одного (неименованного) параметра. Применение функции не ко всем её параметрам, а лишь к первым называется каррированием.
Вот вычурный вариант реализации функции f, где в одной строке происходит два каррирования: функции f_x_k и функции List.sumBy:
let f x =
let f_y_k y k = int ( float k * y )
let adder_on_fk_and_x = List.sumBy (f_y_k x)
adder_on_fk_and_x ksИногда в шутку говорят, что F# не поддерживает функции с несколькими параметрами, а возможность указать несколько параметров при заведении функции не более чем синтаксический сахар. Да и C-подобные языки также не поддерживают функции с несколькими параметрами, просто их адепты об этом не знают.
Но это не совсем верно. Более правильно было бы утверждать, что F# работает так, что как будто не применяет функцию ко всем её аргументам сразу, а делает это последовательно, по аргументу. Сначала применит к первому аргументу, затем результат применения применит ко второму аргументу и т.д. пока не закончатся аргументы.
Это не самая быстрая реализация, тесты показывают, что реализация в процедурном стиле оказывается быстрее:
let f n x =
let mutable acc = 0
for k = 2 to n do
acc <- acc + ( int <| float k * x )
accНо для нашей задачи сойдёт и не самая быстрая.
Численное решение "в лоб"
Теперь можно приступить к решению задачи. Раз математическое решение сходу придумать не удалось, будем использовать численное. Договоримся, что ограничимся типами float и int, не будем использовать другие числовые типы, которые позволили бы повысить точность решения и/или производительность.
Здесь следует заметить, что нам сложно будет перепутать значение, выданное функцией f, от её аргумента, т.к. они будут иметь разные типы, а F# не делает неявных преобразований типов.
Итак, нужно придумать численный метод. Самое простое - взять какое-нибудь конечное множество точек на промежутке [0;1), да и подсчитать кол-во различных значений, которое выдаёт функция на его элементах. Такой подход не гарантирует, что будут собраны все значения. Но, если окажется, что он выдаст все 54 целые числа от 0 до 53, то задача будет решена.
Совсем "в лоб"
В качестве такого множества будем брать значения на промежутке [ 0; 1 ) отстоящие друг от друга на одном и том же расстоянии. Такое множество легко сгенерировать как список при помощи оператора ранжирования ..
[ 0. .. step .. 1. - step ](Хотя в документации это не сказано, эту конструкцию можно использовать не только для целочисленных типов.)
В качестве накопителя получаемых значений функции f будем использовать тип Set<int>. Чтобы добавить к множеству элемент, служит функция Set.add. Она получает на вход элемент и множество, изготавливает копию множества и добавляет к копии элемент, если этого элемента ещё не имеется. Таким образом, множество, к которому она была применена, остаётся не изменённым, что соответствует подходам функционального программирования.
Итак:
let bruteForce (step:float) aSet x1 x2 =
List.fold ( fun accSet x -> Set.add (f x) accSet ) aSet
[ x1 .. step .. x2 - step ]Разъяснения по синтаксису
List.fold принимает 3 параметра
функцию-сворачиватель от двух параметров,
начальное значение,
список.
Функция‑сворачиватель записана в круглых скобках как лямбда‑выражение и не имеет имени. Её тело применяет f к её второму аргументу x. Затем при помощи Set.add дополняет результатом применения множество, полученное во втором аргументе accSet.
Работает List.fold так. Сначала применяет функцию-сворачиватель к начальному значению и первому элементу списка, затем к тому, что получилось, и второму элементу списка снова применяет функцию-сворачиватель, и т.д., пока не закончится список. Возвращает она последнее применение функции сворачивателя. Таким образом, второй аргумент у функции-сворачивателя представляет собой значение состояния, "накопленного" на момент данного вызова.
Вот, например, функция, которая записывает в строку через запятую все элементы списка целых чисел (в её теле для функции-сворачивателя заводится именованная величина addNumberToString):
let makeCSV ints =
let addNumberToString s (i: int) =
if s = "" then
string i
else
s + "," + string i
List.fold addNumberToString "" intsПоследний параметр функции пришлось снабдить аннотацией типа, т. к. по операциям с этим параметром в теле функции его тип невозможно вывести.
Тело addNumberToString состоит из одного, хоть и многострочного, выражения, представляющего собой условный оператор. Каждая его ветка возвращает значение типа string.

Вот, для примера, функция, перемножающая элементы в списке, и её применение для вычисления факториала:
let multiplyList multipliers =
List.fold ( * ) 1 multipliers
multiplyList [ 1 .. 5 ]Протестируем с шагом, генерирующем пустой список:

Тест пройден, на пустом списке получили пустое множество (при преобразовании множества в текст используются квадратные скобки).

(Если ячейка заканчивается выражением, то интерпретатор после выполнения ячейки заводит или перезаводит специальную величину c именем it для хранения значения этого выражения.)
Наверное, значения функции f неравномерно распределяются по промежутку [0;1)

Заметим, что здесь мы переиспользуем имя theSet: заводим новую величину с тем же именем, причём значение новой величины вычисляется при помощи старой величины. Прежняя величина с именем theSet теперь потеряна, но она нам и не нужна. Интересно, что такое переиспользование имени не допускается в рамках ячейки: если в ячейке заводится именованная величина вне блока кода (т.е. величина, которая станет доступна в других ячейках), то в этой же ячейке нельзя завести другую величину с таким же именем.

С уменьшением шага растёт время выполнения.
Понятно, что сходу решить задачу этим методом не получилось. Попробуем оптимизировать функцию bruteForce.
Избавимся от лишних вызовов Set.add
На каждом элементе списка функция bruteForce вызывает Set.add, и каждый раз Set.add делает проверку наличия f x во множестве, сравнивая его с элементами в составе множества. Если организовать из элементов бинарное сбалансированное дерево, то количество этих сравнений логарифмически зависит от количества элементов в составе множества. Если множество состоит из 3 элементов, то может потребоваться до двх сравнений, если из 31, то - до 5 сравнений. К сожалению, почти в половине случаев придётся выполнять максимальное количество сравнений на сбалансированном дереве. Если же запоминать результат применения f на предыдущем x, то можно вызывать Set.add только в тех случаях, когда результат применения не равен предыдущему. Для этого придётся передавать в параметре состояния функции Set.fold помимо множества, где накапливаются значения, ещё и последнее значение, которое в него было добавлено.
Получается, тип этого параметра должен быть агрегатным. Мы могли бы реализовать этот тип в виде записи с именованными полями или даже в виде именованного класса или структуры. Но проще воспользоваться кортежем из двух элементов:
let process_X ( aSet, lastValue ) x =
let value = f x
if value > lastValue then
Set.add value aSet, value
else
aSet, lastValueРазъяснения по синтаксису
Для конструирования кортежа служит запятая. Приоритет у этого оператора низкий, поэтому кортежи часто приходится заключать в скобки.
В отличие от списка, массива или множества, где все элементы должны быть одного типа (или экземплярами классов, наследуемых от одного и того же класса), кортеж может состоять из элементов различных типов.
Второй параметр функции в её заголовке представляет собой шаблон для кортежа из двух элементов. Для конструирования шаблона кортежа также служит запятая.
Если в кортеже только два элемента, то к нему можно применять функции fst и snd, которые возвращают первый и последний элемент соответственно:
let process_X setWithLastValue x =
let value = f x
if value > snd setWithLastValue then
Set.add value (fst setWithLastValue), value
else
fst setWithLastValue, snd setWithLastValue Другой вариант обойтись без шаблона параметра – обозвать элементы кортежа при помощи let (да, эта инструкция так умеет, если указать не единичное имя а шаблон с именами)
let process_X setWithLastValue x =
let aSet, lastValue = setWithLastValue
let value = f x
if value > lastValue then
Set.add value aSet, value
else
aSet, lastValueТ.к. код функции-свёртки вынесен в отдельную величину, тело функции btuteForce можно будет записать короче.
let bruteForceOptmzd1 (step:float) smartAcc x1 x2 =
fst <| List.fold process_X smartAcc [ x1 .. step .. x2 - step ]Обратите внимание, что интерпретатор F# в отличие от Питона при переиспользовании имени не перевычисляет (и уж тем более не перекомпилирует автоматически) никакие другие величины, где эта величина используется. Более того, Поэтому, чтобы не запутываться, лучше заводить улучшенные версии функции под другими именами.
Опробуем:

Увеличение производительности существенное.
Введём рекурсию
С уменьшением шага возрастает не только время вычисления, но и использование памяти, ведь код сначала генерирует весь список, а потом последовательно применяет к его элементам функцию f. Любой экземпляр множества, создаваемый в теле функции, не занимает много места, ведь в нём может оказаться не более 55 элементов. При этом «отработанный» экземпляр множества собирает сборщик мусора, и память, которую он занимал, переиспользуется.
Если на компьютере, где доступно много памяти, а процессор не очень быстрый, запустить наши вычисления с достаточно маленьким шагом, то появится время подумать. И тогда может посетить гипотеза, что генератор списка натыкается на такой x, что его сумма с величиной шага оказывается равной тому же самому x (что возможно из-за округления вследствие особенностей арифметики чисел с плавающей точкой), другими словами, на такой x, который невозможно увеличить. В экспериментах с малым шагом в конструкции [ x1 .. step .. x2 - step ] автору не удалось подобрать такие x1 и x2, чтобы произошло зацикливание. Примечательно, что в конструкции допускается непостоянный шаг, вот, например, случайное блуждание с равномерно распределённым шагом от -0.5 до 0.5 в интервале от 0 до 1:

(В половине случаев этот код выдаёт пустой список.)
Однако проведённые автором эксперименты показали, что эта конструкция ведёт себя не постоянно. С одной стороны она может сгенерировать список с повторяющимися элементами. А с другой стороны количество элементов в списке может изменяться при смещении x1 и x2 на одинаковое число. Другими словами, выражение
List.length [ x1 ... step … x2 ] = List.length [ x1 + shift ... step … x2 shift ] не всегда выдает значение true.
В общем, эта конструкция не годится для наших прецизионных вычислений, поэтому нужно генерировать x вручную, обрабатывая ситуацию, когда невозможно вычислить следующий x:
let nextX step x =
let res = x + step
if x >= res then
failwithf "Невозможно вычислить следующий x, текущий равен %150.149f" x
resВ качестве такого множества будем генерировать список чисел от 0 до 1 ( но не включать саму единицу) с равным шагом.
let bruteForce (step:float) x1 x2 aSet =
List.fold ( fun accSet x -> Set.add (f x) accSet ) aSet
[ x1 .. step .. x2 - step ]Реализуем наш алгоритм через рекурсию:
let rec bruteForceRecursive (step:float) smartAcc x1 x2 =
if x1 >= x2 then // заканчиваем рекусрию
fst smartAcc
else
bruteForceRecursive step (process_X smartAcc x1) (nextX step x1) x2Разъяснения по синтаксису
Ключевое слово rec делает доступным в теле заводимой функции её саму под её же именем, что даёт возможность организовать рекурсию, т.е. составить код, который будет применять функцию в её же теле. Если убрать это ключевое слово, то имя заводимой функции в её теле будет представлять величину, заведённую с этим же именем в другой ячейке, а если величины с этим именем не было заведено, то интерпретатор выдаст ошибку.
Производительность у bruteForceRecursive оказалась лучше на целый порядок. Кроме того, можно обнаружить, что уменьшение шага не приводит к увеличению памяти! Как такое возможно, ведь для каждого x должен в стеке выделяться фрейм для вызова функции? На самом же деле при каждом рекурсивном вызове используется один и тот же фрагмент памяти. Это называется оптимизацией хвостовой рекурсии. Такое возможно потому, что последней инструкцией в теле рекурсивной функции является её применение, после выполнения применения нет необходимости хранить её аргументы.
Другой способ избежать конструирование в памяти коллекции всех x – использовать генератор последовательности. Но его также придётся реализовать через рекурсию.
let rec xSeq step x1 x2 =
seq {
if x1 < x2 then
yield x1
yield! xSeq step (nextX step x1) x2
}Разъяснения по синтаксису
Генератор последовательности (или выражение последовательности) не генерирует всю последовательность сразу, а поставляет элементы по мере того, как они оказываются нужны потребителю, поэтому в памяти не будет храниться коллекция всех x. Он начинается со слова seq. После него в фигурных скобках располагается блок кода, содержащий инструкции yield и yield!. Когда потребителю нужен следующий элемент последовательности, этот код исполняется до инструкции yield включительно, в ней содержится выражение для вычисления значения этого элемента. При следующем обращении к генератору последовательности код продолжает выполняться со следующей инструкции.
Выполните следующий код, чтобы понять, как работает генератор последовательности:
let twoNumbers =
seq {
printfn "twoNubers: Начинаю выдавать элементы последовательности."
printfn "twoNubers: Выдаю первый элемент."
yield 1
printfn "twoNubers: Первый элемент выдан."
printfn "twoNubers: Выдаю второй элемент."
yield 2
printfn "twoNubers: Второй элемент выдан."
printfn "twoNubers: Последовательность закончилась."
}
printfn "Перед началом использования последовательности."
for e in twoNumbers do
printfn "Получен элемент %A" e
printfn "По завершении использования последовательности." let bruteForceRecursiveOnSeq step accSmart x1 x2 =
Seq.fold process_X accSmart <| xSeq step x1 x2
|> fstОднако такой вариант улучшает производительность не на порядок, а в 2-3 раза, т.к. расходует процессорное время на взаимодействие с генератором.
Многопоточность
Разобьём промежуток на несколько сегментов и применим к каждому из них функцию bruteForceRecursive в отдельном потоке выполнения. Так как такой приём, возможно, может пригодиться и для других методов, заведём функцию, которая будет способна принимать на вход процедуру обработки, применяемую к границам произвольного сегмента отрезка [ 0 ; 1 ].
open System.Threading
let processSubSegmentsAsyncronously tQty processSubSegment =
let asyncs = [
for segmentNo in 1 .. tQty ->
async {
let x1 = float (segmentNo - 1) / float tQty
let x2 = min 1. <| float segmentNo / float tQty
let threadId = Thread.CurrentThread.ManagedThreadId
Console.WriteLine
$"(ThreadId={threadId}) Processing the segment [ {x1} ; {x2} ]"
let t = DateTime.Now
let res = processSubSegment x1 x2
let spent = (DateTime.Now - t).TotalMilliseconds
Console.WriteLine
$"(ThreadId={threadId}) Processed the segment [ {x1} ; {x2} ], spent {spent} ms"
return res
}
]
Async.Parallel asyncs |> Async.RunSynchronously Разъяснения по синтаксису
open – инструкция управления областью видимости.
open System.Threading расширяет область видимости пространством имён System.Threading, где размещён дотнетовский класс Thread. Без этой инструкции пришлось бы дополнять имя класса этим пространством имён: System.Threading.Thread.
Величина asyncs в теле функции представляет собой список. Он конструируется при помощи цикла for и выражения, которое, используя «переменную» цикла, выдаёт значение для каждого элемента списка, вычисляющего элементы списка. Заголовок цикла и выражение в этой конструкции разделяются оператором ->.
Поэкспериментируйте:

В последней строке тела функции processSubSegmentsAsyncronously к списку asyncs применяется функция Async.Parallel, а затем оператор |> применяет к получившемуся результату функцию Async.RunSynchronously.
В отличие от основного оператора применения оператор |> применяет свой правый операнд к левому, а не наоборот. Выше встречается симметричный оператор применения <|, он применяет свой левый операнд к правому. Приоритет у операторов <| и |> ниже приоритета арифметических операторов:

Часто эти операторы используются, чтобы уменьшить в коде количество круглых скобок.
Если перед строковым литералом поставить знак $, то фрагменты литерала, заключённые в фигурные скобки, будут интерпретированы как выражения. Интерпретатор преобразует такой литерал в строковую константу, заменив эти выражения их значениями, преобразованными к строке:

Поддерживаются также блоки кода, заканчивающиеся выражением:

(не повторять же для каждого корня одно и то же выражение, которое различается лишь оператором ????)
Конструкция async { … } предназначена для организации многопоточных вычислений. Результат выражения async { … } – код, подготовленный к исполнению в отдельном (может быть) потоке. Async.Parallel подготавливает коллекцию таких кодов к одновременному исполнению в различных потоках, а Async.RunSynchronously запускает их исполнение, при необходимости заводя новые потоки в пуле потоков приложения. Async.RunSynchronously также собирает в массив результаты исполнения каждого кода и завершается, когда каждый код в списке окажется исполненным.
Бо́льшая часть кода в фигурных скобках служит для диагностики. К сожалению, в многопоточных задачах следует избегать printf и printfn, т.к. это может приводить к смешиванию вывода из различных потоков. А вот функции вывода у класса Console потокобезопасны, пока один вызов не выдаст все символы в поток, вызов из другого потока не начнёт их выдавать.
Т.к. ранее мы зачем-то вынесли в параметры функции bruteForceRecursive границы промежутка, причём в последние параметры, теперь bruteForceRecursive после каррирования можно использовать в качестве аргумента processSubSegmentsAsyncronously. Поскольку bruteForceRecursive возращает множество целых чисел, processSubSegmentsAsyncronously возвратит массив множеств, которые придётся объединять в одно множество при помощи функции Set.union.

Опять значительный прирост производительности! При помощи Монитора ресурсов Windows можно посмотреть, как запуск загружает ядра процессора. Теперь нам доступны более мелкие шаги.
Кажется, мы увлеклись этим численным методом. Ведь на промежуток [0;1) приходится огромное количество значений типа float. Гипотетический процессор с 48 ядрами, каждое из которых за одну секунду сможет обработать 3 млрд значений x, за целый год обработает лишь 243 значения:

Причём, на одно значение требуется явно не один такт, а во много-много раз больше (такая производительность пока недостижима для промышленности). В то же время лишь на мантиссу в типе float приходится вовсе не 43 бита, а 52. Поэтому перебрать все возможные значения этого типа не представляется возможным.
Даже добротная реализация описанного выше метода не получит высокую оценку на олимпиаде по программированию, т. к. он не представляется надёжным и требует много вычислительных ресурсов.
Численное решение делением отрезка пополам
Другой способ решения - отыскать все точки разрывов нашей кусочно-постоянной неубывающей функции на отрезке [ 0; 1 ], посчитать их количество и прибавить единицу, если в точке x = 1 разрыва не оказалось.
Если для каких-либо x1 и x2 f(x2) - f(x1) = 1, то на отрезке [ x1; x2 ] функция имеет ровно один разрыв ( и принимает ровно два значения ). Если f(x2) - f(x1) > 1, то кол-во разрывов может быть больше единицы. Тогда разобьём отрезок [ x1; x2 ] на два отрезка, скажем, посредине, и в каждом из этих двух отрезков будем искать разрывы. Чтобы не выполнять слишком много циклов на скачке высотою больше единицы, придётся задать величину точности локализации разрыва - минимальную длину отрезка, при достижении которой прекращать дальнейшие итерации.
Конечно, если взять слишком большое значение этой величины, то можем получить отрезок меньшей длины, на котором имеется более одного разрыва. Тогда метод выдаст неверный результат.
Первый шаг к реализации этого метода – закодировать добротную функцию, которая выдаёт какое-либо значение типа float на заданном интервале (желательно середину) или определяет, что такого значения не имеется:
let getBetween x1 x2 =
let x12 = ( x1 + x2 ) / 2.
if x1 < x12 && x12 < x2 then
Some x12
elif Double.BitIncrement x1 < x2 then
Some <| Double.BitIncrement x1
else NoneРазъяснения по синтаксису
Some и None – имена вариантов размеченного объединения, которое «встроено» в язык. Разработчики языка назвали этот тип данных option.
Размеченные объединения состоят из нескольких именованных вариантов. Варианты одного размеченного объединения могут иметь различные типы данных. Именованный вариант может также обозначать понятие предметной области и не иметь типа данных вообще. Каждый экземпляр размеченного объединения представляет собой значение одного из его вариантов, причём этот вариант определён в рантайме.
option – это параметризованный тип, он дополняет множество значений своего типа-параметра специальным значением None, семантика значения None – отсутствие значения типа-параметра. Тип option не поддерживает операции, которые определены для значений его типа-параметра, т. к. эти операции не определены для значения None.
Вероятно, для любой упорядоченной пары значений x1 и x2 типа float их полусумма либо попадает в интервал ( x1; x2 ) и не совпадает ни с x1, ни с x2, либо данный интервал не содержит ни одного значения типа float и метод BitIncrement не поможет его получить. Многие специалисты по численным методам наверняка смогут это подтвердить или опровергнуть.
Можно предположить, что далее будет удобно оперировать полноценным типом, представляющим сведения о ступеньке графика функции f, т. е. значение, которое выдала функция, наименьший известный аргумент, на котором она выдаёт это значение, и наибольший аргумент. Пусть этот тип будет записью с функциями-членами, которые помогут нам не путаться с при конструировании экземпляров данного тип.
type Plate =
{
/// Высота расположения ступеньки относительно нуля (а не предыдущей ступеньки)
value : int
/// Начало ступеньки по оси X
xLeft: float
/// Окончание ступеньки по оси X
xRight : float
}
/// создаёт ступеньку из одной точки
static member create x y = { xLeft = x; xRight = x; value = y }
static member createFromX x = { xLeft = x; xRight = x; value = f x }
member this.extendBy x = { this with xLeft = min this.xLeft x; xRight = max this.xRight x; }
member this.extendToLeftBy x = { this with xLeft = min this.xLeft x; }
member this.extendToRightBy x = { this with xRight = max this.xRight x; }
Разъяснения по синтаксису
В отличие от кортежа поля записи именованные. Они перечисляются в фигурных скобках.
Чтобы создать у записи или класса экземплярный, т.е. не статический метод, необходимо придумать имя для обозначения экземпляра. В качестве такого имени часто используют имя this. Имя this не встроено в язык, вместо него можно использовать и любое другое имя. Через это имя осуществляется доступ к членам экземпляра в теле метода. Языки программирования почему-то бедны на местоимения.
Методом может являться функция с одним или несколькими параметрами, а также вычисляемое поле.
Создавать экземпляры записей "с нуля" не очень-то удобно, т.к. приходится перечислять каждое поле и указывать после знака равенства выражение для вычисления его значения. Поэтому записи часто снабжают статическими методами, которые конструируют экземпляры.
Зато легко создавать модифицированные копии экземпляров через конструкцию { ... with ... } ? , в которой после with нужно указывать только модифицируемые поля и выражения для их значений.
Теперь становится очевидно, сколь недальновидно мы поступали, сохраняя лишь значения, выдаваемые функцией f, и теряя аргументы, на которых эти значения были получены. А ведь она вызывалась уже буквально миллиарды раз! Можно же было бы завести массив для этих ступенек и при каждом вызове аккумулировать в нём полученные сведения!
Ну да ладно, впредь нужно быть осмотрительнее, меньше писать код, больше размышлять...
Далее нам необходимо реализовать алгоритм, который по интервалу и значениям функции f на его концах выдаёт заключение о наличии разрывов и их количестве: ни одного, ровно один, один или несколько. В языке F# и в его стандартных библиотеках не имеется какой-либо именованной встроенной величины, обозначающей абстрактное положительное количество, большее единицы. Конечно, можно условиться обозначать его, скажем, значением 10. Но тогда об этом нужно помнить.
Чтобы не заводить тип, который будет возвращать этот алгоритм, реализуем его в виде параметрического многовариантного активного шаблона сопоставления:
let (|NoDiscontinuity|JustOneDiscontinuity|MaySeveralDiscontinuities|) (delta, plate1, plate2) =
match plate2.value - plate1.value with
| 0 -> NoDiscontinuity
| 1 -> JustOneDiscontinuity
| _ ->
if plate2.xLeft - plate1.xRight <= delta
then JustOneDiscontinuity
else MaySeveralDiscontinuitiesРазъяснения по синтаксису
Активный шаблон похож на функцию и имеет тело (собственно, он и является функцией и может быть применён). Данный многовариантный шаблон имеет варианты, обозначенные именами NoDiscontinuity, JustOneDiscontinuity и MaySeveralDiscontinuities. Когда нужно будет сопоставить что-либо c этими вариантами, интерпретатор выполнит тело данного активного шаблона и в результате будет определён один из этих трёх вариантов.
Сопоставление происходит при вычислении выражения вида match … with (которая по счастливой случайности также используется в теле данного шаблона).
Конструкция match часто используется программистами подобно конструкции switch в C-подобных языках. Эта конструкция как и оператор if-then-else представляет собой выражение. Оно вычисляется следующим образом. Сначала интерпретатор вычисляет выражение между ключевыми словами match и with. Затем результат пытается сопоставить с шаблонами, размещёнными между | и ->. При успешном сопоставлении возвращает значение, полученное при вычислении выражения после оператора ->. В теле данного активного шаблона используются лишь шаблоны, представляющие собой константы 0 и 1, и «неопределённое местоимение», которое обозначается символом подчёркивания. С ним сопоставляется любое значение. Поэтому если разность высот ступенек оказывается не равной ни 0, ни 1, то произойдёт вычисление условного оператора if-then-else.
Сам активный шаблон будет использован позднее.
Неужели больше нет повода для прокрастинации и уж теперь придётся думать, как реализовать численный метод?
Значит, пришло время для начала завести функцию, которая методом деления пополам локализует самый первый (самый левый разрыв). Пусть она выдаёт кортеж из прилегающих к нему ступенек:
let rec locateDiscontinuity delta plate1 plate2 =
match delta, plate1, plate2 with
| NoDiscontinuity ->
failwith $"Как-то криво вызвали locateDiscontinuity"
| JustOneDiscontinuity -> // Не будем уменьшать интервал между ступеньками
plate1, plate2
| MaySeveralDiscontinuities ->
match getBetween plate1.xRight plate2.xLeft with
| None -> (plate1, plate2)
| Some x12 ->
let value12 = f x12
if value12 = plate1.value then
locateDiscontinuity delta ( plate1.extendToRightBy x12 ) plate2
elif value12 = plate2.value then
locateDiscontinuity delta plate1 ( plate2.extendToLeftBy x12 )
else
locateDiscontinuity delta plate1 ( Plate.create x12 value12 )
Разъяснения по синтаксису
В первой конструкции match будет сопоставляться кортеж delta, plate1, plate2. Т.к. в первом варианте выражение для сопоставления представляет собой имя варианта нашего активного шаблона, то его тело будет выполнено, после чего выполнится соответствующее выражение после оператора ->.
Для варианта MaySeveralDiscontinuities это выражение также является конструкцией match. Но в этот раз никакие активные шаблоны (т.е. шаблоны, для которых имеется исполняемый код) не задействованы. Функция getBetween выдает либо None, либо Some, инициализированный каким-либо значением. Синтаксис сопоставления с шаблоном позволяет присвоить этому значению имя (в данном случае присваивается имя x12).
Заведём начальные ступеньки

и запустим сразу с нулевой дельтой

Работает, причём довольно быстро! Значит, она выжимает наибольшую возможную точность из типа float.
Теперь можно найти все ступеньки вручную:

Но лучше этот труд автоматизировать.
Для этого немного улучшим функцию locateDiscontinuity. Дело в том, что она, когда между первой ступенькой plate1 и второй ступенькой plate2 обнаруживает новую ступеньку, не возвращает вторую ступеньку, которая к этому моменту может быть уже расширена, а продолжает дальше рекурсию со ступенькой plate1 и новой ступенькой.
Сделаем её чуть более ленивой, пусть она, как только обнаружит новую ступеньку, не продолжает рекурсию, а возвращает и новую ступеньку и уже имеющиеся расширенные.
let rec locateDiscontinuityLazy delta plate1 plate2 =
match delta, plate1, plate2 with
| NoDiscontinuity ->
failwith $"Как-то криво вызвали locateDiscontinuity"
| JustOneDiscontinuity -> plate1, None, plate2
| MaySeveralDiscontinuities ->
match getBetween plate1.xRight plate2.xLeft with
| None -> (plate1, None, plate2)
| Some x12 ->
let value12 = f x12
if value12 = plate1.value then
locateDiscontinuityLazy delta ( plate1.extendToRightBy x12 ) plate2
elif value12 = plate2.value then
locateDiscontinuityLazy delta plate1 ( plate2.extendToLeftBy x12 )
else
plate1, Some ( Plate.create x12 value12 ), plate2(Более правильно было бы сказать «возвращает экземпляры уже имеющихся ступенек», т.к. методы типа Plate создают копии своего экземпляра, а не сам экземпляр.)
Теперь создадим рекурсивный генератор последовательности ступенек, который накапливает их в списке и по мере того, как они становятся ненужными, выдаёт их в последовательность.
let rec generatePlates delta (plates : Plate list) =
seq{
match plates with
| plate1 :: plate2 :: rest ->
let plate1Next, middle, plate2Next =
locateDiscontinuityLazy delta plate1 plate2
match middle with
| Some plate12 ->
yield!
plate1Next :: plate12 :: plate2Next :: rest
|> generatePlates delta
| None ->
yield plate1Next
yield! plate2Next :: rest |> generatePlates delta
| [ plate ] -> yield plate
| [ ] -> ()
}Разъяснения по синтаксису
Оператор :: ассоциативен справа. С его помощью можно сконструировать шаблон сопоставления, который присвоит имя головному элементу в списке и списку из остальных его элементов. (Кстати, как это часто бывает с операторами, конструирующими шаблоны, основное назначение этого оператора другое. Он также конструирует список путём добавления элемента в начало существующего списка.) Интересно, что при конструировании шаблонов сопоставления допускается использовать один шаблон в составе другого.
Воспользуемся:

Время вычисления – менее 100 мс, причём с максимально возможной точностью и без многопоточности!
Проверим, что из себя представляет последняя ступенька:

Она вне промежутка [ 0; 1 ), значит, на него приходится всего 32 ступеньки.
... Хотя новые значения функции f не были найдены, стало очевидно, что они и не могут быть найдены, если в качестве её аргументов использовать значения типа float.
Решение для математической олимпиады
Данная кусочно-постоянная (и потому кусочно-непрерывная) функция делает скачок (т.е. разрыв) только на тех значениях x, на которых делает скачок хотя бы одна из функций fk . А функции fk делают скачок только на дробных числах со знаменателем от 2 до 10. Поэтому задача сводится к подсчёту несокращаемых неотрицательных дробных чисел, меньших единицы, знаменатель которых не больше 10.
Их несложно подсчитать глазами и руками, но можно при этом и ошибиться. Составим код, который сделает это автоматически.
Сперва заведём функцию, которая определяет, можно ли сократить дробь со знаменателем k и числителем n. Если дробь можно сократить, то существует такое простое число, на которое делятся и её числитель, и её знаменатель. Число 10 не превосходят только 4 простых числа.
/// Определяет, является ли несократимой дробь n / k
let isIrreducible k n =
List.exists
<| ( fun p -> k % p = 0 && n % p = 0 )
<| [ 2; 3; 5; 7 ]
|> not % - оператор получения остатка от деления, && - логическое И.
А теперь:
// … для каждого k
ks |>
(
// посчитаем кол-во несократимых дробей при помощи функции:
( fun k -> List.filter (isIrreducible k) [ 1 .. k - 1 ] |> List.length )
// И сложим эти кол-ва:
|> List.sumBy
)
// И добавим единицу, т.к. значение 0 не было посчитано:
|> ( + ) 1Комментарии (9)

ProMix
11.04.2023 02:13Автору статьи не удалось придумать более
подходящее имя, чтобы оно помогало понять код, а не запутывало.Любое имя длиннее двух букв помогало бы. Например multiply, multiplyDelefate, multiplyAndFloor
Применение функции не ко всем её параметрам, а лишь к первым называется каррированием.
По-моему не самая лучшая формулировка - функция-то в любом случае применяется ко всем параметрам. Это скорее получение новой функции из старой с помощью фиксации определённых параметров
Вообще впечатление от языка такое, будто это bash. Есть какая-то причина для динамической типизации в языке?

whoisking
11.04.2023 02:13Вообще впечатление от языка такое, будто это bash. Есть какая-то причина для динамической типизации в языке?
Она статическая

belch84
11.04.2023 02:13Стало интересно, как же выглядит график такой функции
График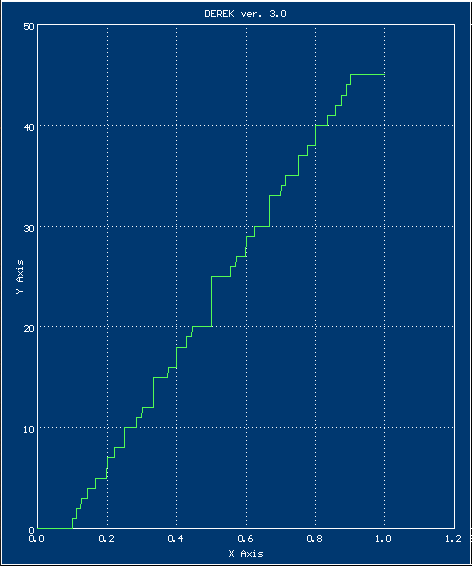
Для решения совсем уж в лоб можно руками (т.е. глазами) подсчитать количество горизонтальных участков, или попросить это сделать какой-нибудь ИИ

ermouth
11.04.2023 02:13Можно сдвинуть график на пиксель влево, сделать and с исходным вариантом и посчитать к-во начал отрезков (перепад 0->1).
Или даже просто посчитать к-во левых верхних углов (нет соседей слева и сверху).



vbra2022
Извините, могу быть не прав, но промежуток от 0 (включая 0) до 1 (не включая 1).
gabirx
Первая и единственная мысль возникла, что это именно так. Интересно будет узнать, что это может быть не так
gabirx
а, там по контексту подходит " и не меньше 0"