
Привет, Хабр!
Меня зовут Серов Александр, я участник профессионального сообщества NTA.
В данном посте я расскажу о возможностях применения параллельных вычислений в интерактивной среде Jupyter notebook языка Python.
Быстрая навигация по посту
Для чего нам необходим параллелизм?
Параллелизм играет важную роль в задачах Data Science, так как может значительно ускорить вычисления и обработку больших объемов данных. Вот некоторые основные причины, почему мультипроцессинг важен для этих задач:
Ускорение вычислений: многие задачи в DS, такие как обучение моделей машинного обучения, кластеризация, обработка изображений и анализ больших данных, являются вычислительно интенсивными. Использование параллельных вычислений позволяет распределить работу между несколькими ядрами процессора или даже между несколькими компьютерами, что приводит к существенному ускорению выполнения задач.
Обработка больших объемов данных: параллельные вычисления позволяют эффективно распараллелить обработку данных, разделив ее на более мелкие части и выполняя их одновременно.
Оптимизация гиперпараметров: за счет параллельного выполнения экспериментов с различными значениями гиперпараметров можно ускорить процесс поиска оптимальных параметров модели.
Обработка потоковых данных: может быть необходимо обрабатывать потоковые данные в реальном времени. Мультипроцессинг позволяет эффективно обрабатывать и анализировать потоки данных, особенно в случае высоких нагрузок и необходимости обработки данных в режиме реального времени.
В языке Python уже есть реализация параллелизма на основе базового модуля — multiprocessing. Тогда почему в Jupyter notebook он не будет работать?
Почему не работает multiprocessing?
В Jupyter Notebook возникают проблемы при использовании модуля multiprocessing из‑за его особенностей взаимодействия с интерактивной средой Jupyter. Эти проблемы связаны с тем, что Jupyter Notebook запускает ядро Python в собственном процессе, который уже выполняет код ячеек.
Модуль multiprocessing в Python использует форкирование процессов для достижения параллельного выполнения. Однако в Jupyter Notebook уже есть запущенный процесс Python, и при попытке использования multiprocessing в ячейке происходит попытка создания нового дочернего процесса внутри уже существующего процесса, что вызывает конфликт.
Также следует отметить, что Jupyter Notebook сам по себе является интерактивной средой, где можно выполнять код в ячейках в любом порядке и в любое время. Однако multiprocessing требует выполнения кода в основном (главном) модуле программы, что делает его работу с Jupyter Notebook сложной.
Joblib vs. multiprocessing
Библиотека joblib предоставляет простой интерфейс для параллельного выполнения задач на нескольких ядрах процессора, и она может быть использована в Jupyter Notebook для задействования параллелизма.
Основное отличие между multiprocessing и joblib заключается в том, как они взаимодействуют с интерпретатором Python. В отличие от multiprocessing, joblib использует фоновые процессы, которые запускаются независимо от основного процесса Jupyter Notebook. Таким образом, joblib избегает проблем, связанных с созданием дочерних процессов внутри уже существующего процесса.
Перейдем к практической демонстрация работы кода без использования параллельных вычислений.
Monkey sort без параллельных вычислений
Для начала необходимо сымитировать вычислительную функцию с длительным выполнением, из самых известных и простых вариантов это monkey sort — алгоритм сортировки, который проверяет является ли массив отсортированным, если нет, то случайным образом перемешивают до тех пор, пока он не отсортируется. Его средняя асимптотика будет равна O((n+1)!), в среднем, потому что существует фактор случайности и перемешивание может случиться как быстрее, так и дольше, но при применении закона больших чисел, асимптотика устремиться к этому значению.
Импортируем необходимые библиотеки:
from joblib import Parallel, delayed
import pandas as pd
import random
import numpy as np
import warnings
import random
warnings.filterwarnings('ignore')Реализуем алгоритм «самой быстрой сортировки» bogosort (monkey sort) на языке Python:
def bogosort(arr):
def correct(arr, comparator=lambda x: x):
for i in range(1, len(arr)):
if comparator(arr[i - 1]) - comparator(arr[i]) > 0:
return False
return True
while not correct(arr):
random.shuffle(arr)
return arrДля тестирования гипотез сгенерируем двумерный массив, в котором будет 8 случайно расположенных целочисленных значений и всего таких наборов в количестве 1000:
bigdata = np.array([[random.randint(0, 100) for _ in range(8)] for _ in range(1000)])
print(bigdata[:5]) # выводим первые 5 элементов
Проверить работу алгоритма можно на этом наборе данных, для учета времени используем встроенную магическую функцию Python%%time:
%%time
bg = bigdata.copy()
order_bg = list(map(bogosort, bg))
Проверим результаты:
print(order_bg[:5]) # выводим первые 5 элементов
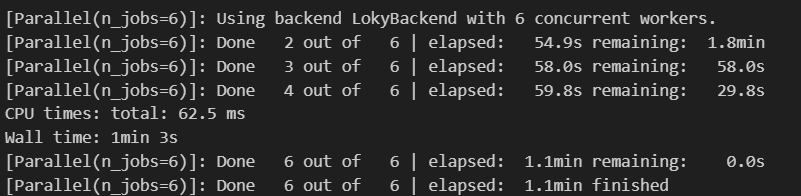
Всё успешно отсортировано за 4 минуты 32 секунды.
А если применить мультипроцессинг?
Теперь решим эту же задачу, применив мультипроцессинг.
Следует отметить, что здесь необходим иной подход к реализации функций, выделим в рамках этой задачи 2 подхода:
Первый подход состоит в декомпозиции задачи и параллельном выполнении вычислительных итераций. Однако, в конкретном случае, у нас есть только одна подзадача — случайное перемешивание. Разделение этой задачи на параллельные части не имеет смысла, поскольку процессор будет тратить время на координацию и синхронизацию параллельных процессов, что может увеличить накладные расходы и замедлить выполнение.
Вместо этого, я предлагаю второй подход — использование разделение данных на партиции и выполнения вычислений для каждой из них. Этот подход похож на методы, используемых в Apache Spark.
Перейдем к написанию кода для второго варианта, в данном случае функция будем сохранена изначальной, и у нас нет необходимости изолировать процесс, а после чего синхронизировать с общей очередью сбора данных, это нам позволяет сделать joblib и lambda функции python:
N_CORES = 12 # количество задействованных ядер процессора
list_array = np.array_split(bigdata, N_CORES)
data = Parallel(n_jobs=N_CORES, verbose=10)(delayed(lambda array: list(map(bogosort, array)))(array) for array in list_array)Joblib предоставляет класс Parallel, который позволяет распределить выполнение итераций цикла или вызовы функций на несколько ядер процессора. Он может использовать различные методы параллелизма, включая использование процессов или потоков. В аргументе функции delayed обозначаю функцию, естественно, без вызова. Дальше должны упомянуть аргумент, для подачи в pipeline функции и объект, из которого его будем брать. Все это оформляется в формате list comprehended.
Помимо lambda, для удобства читаемости, можем объявить функцию multi_bogosort:
def multi_bogosort(ndarray):
return list(map(bogosort, ndarray))И тогда итоговый вариант с ней будет выглядеть, как:
N_CORES = 12
list_array = np.array_split(bigdata, N_CORES)
data = Parallel(n_jobs=N_CORES, verbose=10)(delayed(multi_bogosort)(array) for array in list_array)Обратите внимание, что joblib автоматически обрабатывает разделение данных и сбор результатов, поэтому вам не нужно беспокоиться о явном управлении процессами или потоками.
Посмотрим на время выполнения:

Видим значительное ускорение, но на деле не всё так «идеально», формат данных немного изменился и нам необходимо после разделения их снова слиять, допустим, следующим алгоритмом:
from functools import reduce
merge_data = reduce(lambda x, y: x.extend(y) or x, data)И проверим уже по традиции данные:
merge_data[:5]
Из‑за включения дополнительной предобработки и постобработки результатов, а также координацию и синхронизацию процессоров тратим некоторые время, а следовательно результат не будет иметь чистого t/N_cores зависимости.
Итоговое ускорение процесса с 4 мин 32 секунд (272 секунды) против 44.9 секунд, а это 6-ти кратное увеличение производительности.
Давайте также проведем тест для 6-ти процессоров для сравнения:
%%time
N_CORES = 6
list_array = np.array_split(bigdata, N_CORES)
data = Parallel(n_jobs=N_CORES, verbose=10)(delayed(multi_bogosort)(array) for array in list_array)
merge_data = reduce(lambda x, y: x.extend(y) or x, data)Ниже можно увидеть зависимость времени выполнения от количество задействованных ядер процессора для параллельной функции. (Важно отметить, что пункт с 12 ядрами стоит понимать, как 6 физических + 6 логических, и поэтому не увидели существенного прироста, т.к. 6 логических ядер — это потоки, и здесь уже оказывает влияние GIL).
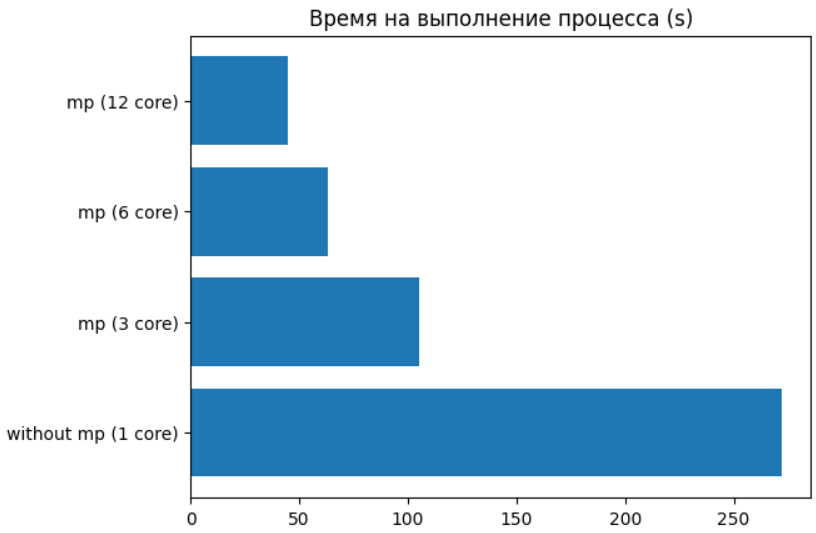
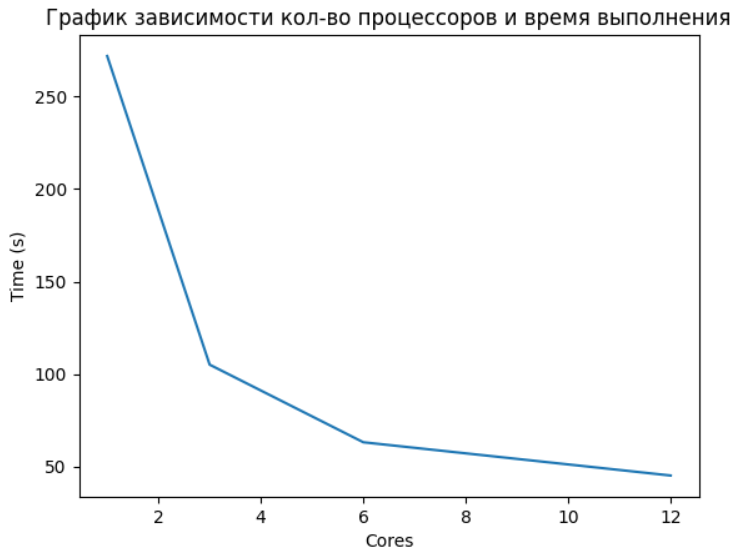
Использование параллельных вычислений может принести значительную пользу в задачах анализа данных и машинного обучения. Особенно это важно, когда работа идет с действительно большими объемами данных. Зачастую в работе специалистов в сфере Data Science наиболее используемых инструмент — это интерактивные среды Jupyter, это обусловлено легкости проводимых экспериментов и тестирование в нём. А без возможности использовать параллелизм — функциональность ограничивается, и в этом случае нас выручает тот самый joblib.
Хочется добавить ещё один пример на реальной задаче в RL, когда нам необходимо найти оптимальное количество кластеров при помощи, так называемого, метода локтя. Кратко: алгоритм работает следующим образом, рассчитывает модель KMeans итеративно для определенной области поиска. После чего — подсчитывает определенную метрику, в данном случае буду использовать силуэт. И по итогу определяем оптимальную метрику, когда увеличения кластеров не даёт существенного прироста, интерпретируя это высказывания в график получаем что‑то наподобие сгиба локтя, когда ошибки становится относительно гладкой.
Развернуть код
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
from sklearn.metrics import silhouette_score
from sklearn import preprocessing
from sklearn.decomposition import PCA
from sklearn.pipeline import Pipeline
from sklearn.base import BaseEstimator, TransformerMixin
from sklearn.model_selection import GridSearchCV
class KMeansWithSilhouette(BaseEstimator, TransformerMixin):
def __init__(self, n_clusters):
self.n_clusters = n_clusters
def fit(self, X, y=None):
self.kmeans = KMeans(n_clusters=self.n_clusters)
self.kmeans.fit(X)
return self
def transform(self, X):
return self.kmeans.transform(X)
def score(self, X, y=None):
labels = self.kmeans.predict(X)
return silhouette_score(X, labels)
def calculate_silhouette_scores(X, cluster_range):
pipeline = Pipeline([
('scaling', preprocessing.StandardScaler()),
('pca', PCA(n_components=2)),
('kmeans', KMeansWithSilhouette(n_clusters=cluster_range))
])
grid_search = GridSearchCV(pipeline, param_grid={}, cv=5, n_jobs=1)
grid_search.fit(X)
return grid_search.best_score_Реализуем функцию вычисления, без параллельного выполнения, также для теста возьмем случайно сгенерированы данные с 7-ю центроидами.
def calculate_elbow(X, cluster_range):
silhouette_scores = []
for n in cluster_range:
score = calculate_silhouette_scores(X, n)
silhouette_scores.append(score)
deltas = np.diff(silhouette_scores)
elbow_index = np.argmax(deltas) + 1
return cluster_range[elbow_index]
X, _ = make_blobs(n_samples=10000, n_features=100, centers=7, random_state=42)
cluster_range = range(2, 15)
start_time = time.time()
elbow_value = calculate_elbow(X, cluster_range)
elapsed_time = time.time() - start_time
print("The optimal number of clusters is:", elbow_value)
print("Execution time:", elapsed_time, "seconds")
За 15,5 секунды просчитал 15 кластеров и выбрал оптимального количество = 3. Теперь сделаем это с применением joblib.
def calculate_elbow(X, cluster_range):
silhouette_scores = Parallel(n_jobs=6)(
delayed(calculate_silhouette_scores)(X, n) for n in cluster_range
)
deltas = np.diff(silhouette_scores)
elbow_index = np.argmax(deltas) + 1
return cluster_range[elbow_index]
X, _ = make_blobs(n_samples=10000, n_features=100, centers=7, random_state=42)
cluster_range = range(2, 15)
start_time = time.time()
elbow_value = calculate_elbow(X, cluster_range)
elapsed_time = time.time() - start_time
print("The optimal number of clusters is:", elbow_value)
print("Execution time:", elapsed_time, "seconds")
Результат существенно сократился в 3 раза, и получился равен = 4.9 секунды.
Важно отметить, что эффективность параллельного выполнения в Jupyter Notebook может быть ограничена некоторыми факторами, такими как наличие глобальной блокировки GIL (Global Interpreter Lock) в интерпретаторе Python. Это может снижать производительность при выполнении CPU‑интенсивных задач, даже при использовании параллельного выполнения. Также играют роль и накладные расходы (планирование, передача, синхронизация) на задействования нескольких ядер. Помимо этого, стоит не забывать про кэш и память. Следовательно необходимо находить «золотую» середину и она разнится от каждой задачи, а также и от архитектуры процессоров.
Заключение
Для достижения оптимального ускорения с помощью мультипроцессинга необходимо тщательно разработать и параллельно выполнить алгоритм, минимизировать коммуникацию и синхронизацию, а также обеспечить равномерное распределение нагрузки между ядрами. Кроме того, использование эффективных методов и техник параллелизации, таких как балансировка нагрузки и разделение данных, поможет максимизировать преимущества мультипроцессинга.
Комментарии (6)

egaoharu_kensei
29.06.2023 19:39Только работал с этой библиотекой и тут же статья - прикольно).
Заметил одну проблему, связанную со многопроцессорностью и многопоточностью: все это плохо работает с random и np.random, когда нужно контролировать состояние рандома - результаты будут отличаться от последовательного исполнения, учтите этот момент.
Например, если вы попробуете реализовать бутстрап вручную и распараллелить его выполнение, то состояние рандома на каждом ядре будет сбрасываться в начальную точку, а не продолжаться как при последовательном выполнении и лучше в этом случае сделать обычный генератор.
Ну а вообще, библиотека очень полезная и не зря используется под капотом в sklearn. Хорошо, что появляются статьи про подобные либы на русском языке.

NewTechAudit Автор
29.06.2023 19:39Добрый день!
Классно что вы делитесь своим опытом использования библиотеки, буду иметь ввиду при ей использовании.
Согласен, библиотека мегаполезная.
Спасибо!

0x0000dead
29.06.2023 19:39Спасибо за статью!
Довольно полезный и наглядный пример с расчетом кластеров в KMeans, но хотелось бы побольше примеров различного использования.

NewTechAudit Автор
29.06.2023 19:39Добрый день!
Спасибо за интерес к посту и подсказку куда в дальнейшем можно развивать исследование возможностей библиотеки.


wilcot
Применение bogosort здесь не очень удачное, так как в случае параллельного выполнения результат получается случайным по отношению к количеству операций. Раз так «быстро» предлагается сортировать, то лучше что-ли через next_permutation делать, сложность получится та же, O(n!) для n различных значений, но результат уже будет более предсказуемым .
NewTechAudit Автор
Добрый день!
Буду иметь в виду и опробую библиотеку на предложенной задаче. Спасибо за комментарий.