Представьте себе набор данных, состоящий из некоторого количества наблюдений. У каждого наблюдения имеется N признаков. Если преобразовать все эти признаки в их числовое представление, то можно будет сказать, что каждое из наблюдений — это точка в N‑мерном пространстве.

Если N — величина небольшая — взаимоотношения между точками будут именно такими, какими их можно представить на интуитивном уровне. Но иногда N достигает огромных значений. Это может произойти, например, когда множество признаков создают посредством прямого кодирования или чего‑то подобного. Для очень больших значений N наблюдения ведут себя так, как если бы они были бы представлены разреженными данными, или так, как если бы расстояния между ними были бы несколько больше, чем можно было бы ожидать.

Это — реальное явление. По мере роста N, при условии, что всё остальное не меняется, объём части N‑мерного пространства, содержащий наблюдения, тоже, в некотором смысле, увеличивается (или, как минимум, увеличивается количество степеней свободы). Увеличиваются и евклидовы расстояния между наблюдениями. Группа точек становится всё более разреженной структурой. Это — геометрическая база для такого понятия, как «проклятие размерности». Подобные изменения в данных влияют на поведение моделей и на приёмы работы, применяемые к наборам данных.

Многое может пойти не так, как ожидается в том случае, если число признаков очень велико. В ситуациях, когда признаков больше, чем наблюдений, обычно возникает переобучение моделей. В многомерном пространстве ухудшается эффективность любых методов, предусматривающих перебор данных (например — GridSearch), так как для того, чтобы уложиться в одни и те же линейные интервалы, нужно будет сделать больше попыток.

Рост числа признаков наблюдений оказывает влияние на любые модели, основанные на расстоянии между наблюдениями или на их близости. Предположим, количество размерностей представляет собой достаточно большую величину. Если взять какую‑нибудь точку наблюдений, то она окажется расположенной очень далеко от всех остальных точек. И, кроме того, расстояния между ней и другими точками окажутся практически одинаковыми. А так как механизмы модели завязаны на расстоянии между точками наблюдений, работа этих механизмов усложнится. Например — в такой ситуации, когда все точки расположены друг от друга на примерно одинаковом расстоянии, не будут нормально работать механизмы кластеризации.

Все эти причины, а так же — многие другие — привели к созданию специальных инструментов. Среди них — метод главных компонент (Principal Component Analysis, PCA) и модель латентного размещения Дирихле (Latent Dirichlet Allocation, LDA). Это — попытка уйти от специфических особенностей пространств с очень большим количеством измерений, попытка свести свойства набора данных к такому количеству измерений, которое лучше соответствует характеристикам той информации, которая в нём содержится.

Истинные масштабы проклятия размерности трудно прочувствовать на интуитивном уровне, а пространства, количество измерений которых превышает 3, чрезвычайно сложно визуализировать. Поэтому предлагаю вашему вниманию двумерные схемы, призванные помочь нашей интуиции. У того, что работа с пространствами больших размерностей может вылиться в массу проблем, есть геометрическое обоснование. Именно визуализацией этих проблем мы тут и займёмся. Если раньше вы такого не видели — результаты могут показаться вам удивительными. Геометрия высокоразмерных пространств гораздо сложнее, чем может себе представить тот, кто раньше о ней не задумывался. Здесь мы задействуем метод Монте‑Карло для визуализации поведения наблюдений с очень большим количеством признаков.

Объём

Представим себе единичный квадрат, центр которого находится в начале координат на координатной плоскости. В этот квадрат впишем круг.

Это — то, с чем мы тут будем работать. А теперь поразмыслим об общем, N‑мерном случае. В трёх измерениях это будет сфера, вписанная в куб. А дальше — будет N‑мерная сфера, вписанная в N‑мерный куб. Это — наиболее общий способ описать интересующую нас конструкцию. Мы, ради простоты, вне зависимости от того, сколько измерений имеет рассматриваемое пространство, будем называть эти объекты «сферой» и «кубом».

Объём куба неизменен, он всегда равняется 1. И тут возникает вопрос: что происходит с объёмом сферы при изменении количества размерностей N?

Ответим на этот вопрос экспериментальным путём, используя метод Монте‑Карло. Сгенерируем очень большое количество точек, распределённых в кубе равномерно, но случайным образом. Для каждой точки вычислим расстояние до начала координат. Если это расстояние меньше 0,5 (это — радиус сферы) — значит, точка будет находиться внутри сферы.

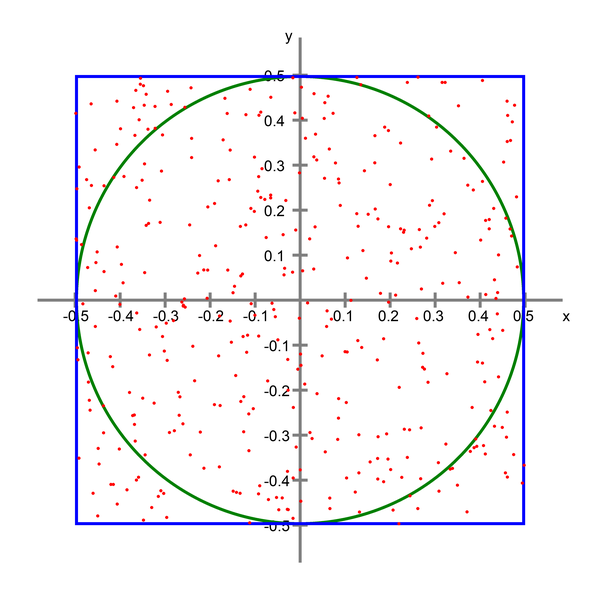
Если разделить количество точек, попадающих внутрь сферы, на общее количество точек, это даст нам примерный показатель отношения объёма сферы к объёму куба. Так как объём куба равен 1 — это отношение будет равно объёму сферы. Это приблизительное значение становится точнее по мере роста количества точек.

Другим словами, отношение внутренние_точки / все_точки позволяет приблизительно определить объём сферы.

Код, который мы рассмотрим ниже, достаточно прост. Так как нам нужно очень много точек, обычных циклов лучше избегать. В подобном коде можно воспользоваться NumPy, но эта библиотека ориентирована исключительно на CPU и на однопоточный режим выполнения, из‑за чего код, где применяется NumPy, будет медленным. Потенциальными альтернативами NumPy являются CuPy (GPU), Jax (CPU/GPU), PyTorch (CPU/GPU) и другие подобные библиотеки. Мы будем пользоваться PyTorch — но код, где применяется, NumPy будет выглядеть практически так же.

Если проанализировать вложенные выражения torch в нашем коде, то окажется, что тут мы генерируем 100 миллионов случайных точек, вычисляем их расстояние до начала координат, вычисляем количество точек внутри сферы и делим это количество на общее число точек. Массив ratio, в итоге, будет содержать сведения об объёме сфер в пространствах различных размерностей.

Настраиваемые параметры этого кода рассчитаны на GPU с 24 Гб памяти. Если будете запускать это у себя — подстройте их под своё оборудование.

device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
# для принудительного использования CPU
# устройство нужно установить в 'cpu'

# уменьшите d_max, если слишком много значений ratio равны 0.0
d_max = 22
# уменьшите n, если вам не хватает памяти
n = 10**8

ratio = np.zeros(d_max)

for d in tqdm(range(d_max, 0, -1)):
    torch.manual_seed(0)
    # скомбинируем большие тензорные операторы для улучшения выделения памяти
    ratio[d - 1] = (
        torch.sum(
            torch.sqrt(
                torch.sum(torch.pow(torch.rand((n, d), device=device) - 0.5, 2), dim=1)
            )
            <= 0.5
        ).item()
        / n
    )

# очистка памяти
torch.cuda.empty_cache()

Визуализируем результаты:

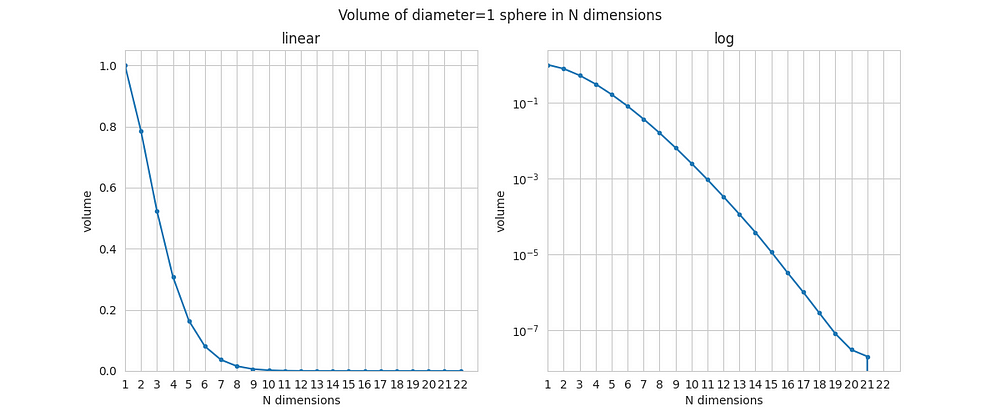
Проверим правильность моделирования. Для N=1 всё предельно просто: и «сфера» и «куб» — это равные отрезки на прямой, «объём» сферы будет равен 1. Для N=2 и N=3 в дело идут формулы, которые изучают в школе. Можно заметить, что наши результаты очень близки к тем, что можно найти по формулам.

А вот по мере увеличения N происходит нечто весьма впечатляющее: объём сферы стремительно приближается к нулю. Он близок к нулю уже тогда, когда N=10. А когда N оказывается больше 20, объём сферы падает до пределов точности чисел с плавающей точкой. Наш код, учитывая то, что мы находим лишь приближённое значение, вычисляет этот объём как 0,0.

>>> print(list(ratio))
[1.0, 0.78548005, 0.52364381, 0.30841056, 0.16450286, 0.08075666, 0.03688062, 0.015852, 0.00645304, 0.00249584, 0.00092725, 0.00032921, 0.00011305, 3.766e-05, 1.14e-05, 3.29e-06, 9.9e-07, 2.8e-07, 8e-08, 3e-08, 2e-08, 0.0]

Одно из объяснений этого явления может выглядеть так: при больших значениях N почти весь объём куба приходится на его углы. Центральная область, содержащая сферу, занимает, в сравнении с другими областями куба, незначительный объём. В высокоразмерных пространствах углы куба оказываются очень важным местом. Большая часть объёма «переходит» в углы. Это происходит очень быстро при росте N.

Вот ещё одна интерпретация происходящего: сфера — это «окрестность» начала координат. По мере роста N точки просто исчезают из этой окрестности. Начало координат — это не нечто особенное, поэтому то, что происходит в окрестности начала координат, должно происходить и в окрестностях всех остальных точек. Само понятие «окрестности» претерпевает большое изменение. Вместе с ростом N у точек в пространстве становится всё меньше и меньше соседей.

Впервые я запустил эту симуляцию много лет назад, и я отчётливо помню то, как меня поразил её результат, а именно — то, как стремительно движется к 0 объём сферы при росте N. После того, как я проверил код и не нашёл в нём ошибок, меня посетила такая мысль: надо сохранить код, заблокировать экран, выйти на улицу, прогуляться и подумать о том, что я только что видел :)

Линейное расстояние

Найдём диагональ куба, воспользовавшись функцией от N. Это легко, так как диагональ равна sqrt(N). Код для таких вычислений слишком примитивен, чтобы его тут показывать. А вот — результаты вычислений.

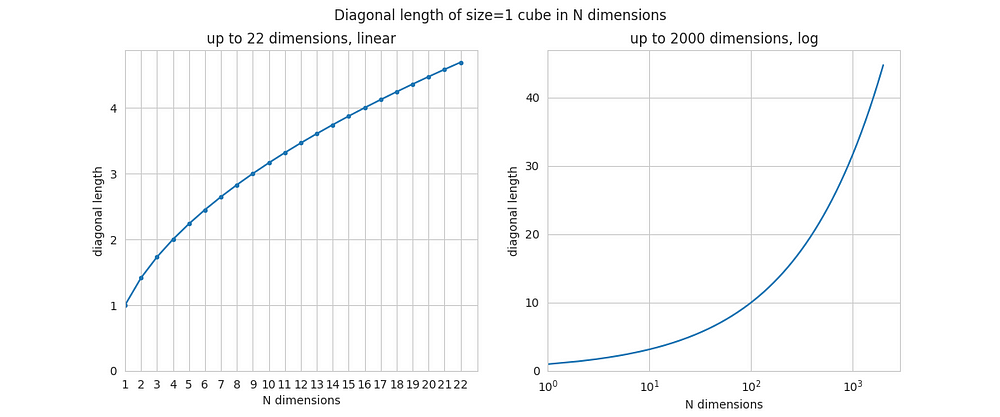
Для случаев N=2 и N=3 проверить эти вычисления можно, основываясь на школьных знаниях (речь идёт о диагонали квадрата и обычного трёхмерного куба). Но по мере увеличения N растёт и длина диагонали. И рост этот ничем не ограничен.

Это может звучать совершенно неправдоподобно, но даже при том, что длина ребра куба остаётся неизменной (и равной 1), его диагональ может иметь сколько угодно большой размер, увеличивающийся при увеличении N. При N=1000 диагональ равна примерно 32. В теории, если длина ребра куба равна 1 метру, существует такое многомерное пространство, в котором длина диагонали куба будет равняться 1 километру.

Даже если длина ребра куба не меняется, его диагональ, по мере увеличения размерности пространства, способна неограниченно расти.

Каждый раз, когда к пространству добавляется новое измерение, у куба появляются новые рёбра и грани, усложняются характеристики его углов, он обретает больше степеней свободы, а его диагональ становится длиннее.

Расстояние между наблюдениями

А как насчёт расстояния между наблюдениями, или расстояния между точками в пространстве? Предположим, мы сгенерировали фиксированное количество случайных точек и решили вычислить среднее расстояние между любыми двумя точками, а так же — среднее расстояние до ближайшего соседа точки. Все точки всегда содержатся в кубе. Что произойдёт со средним расстоянием между точками при росте N? Запустим ещё одну симуляцию.

Обратите внимание на то, что тут применяется консервативный подход к управлению памятью. Это важно, так как используемые тут структуры данных довольно‑таки велики.

n_points_d = 10**3
# сколько пар точек тут имеется
dist_count = n_points_d * (n_points_d - 1) / 2
# мы используем полную попарную матрицу расстояний,
# поэтому каждое расстояние будет вычисляться дважды
dist_count = 2 * dist_count
d_max = d_max_diag

avg_dist = np.zeros(d_max)
avg_dist_nn = np.zeros(d_max)

for d in tqdm(range(d_max, 0, -1)):
    torch.manual_seed(0)
    # генерируем случайные точки
    point_coordinates = torch.rand((n_points_d, d), device=device)
    # вычисляем разности координат точек по всем осям
    coord_diffs = point_coordinates.unsqueeze(1) - point_coordinates
    del point_coordinates
    # возводим в квадрат полученные разности координат
    diffs_squared = torch.pow(coord_diffs, 2)
    del coord_diffs
    # вычисляем расстояния между каждой парой точек
    distances_full = torch.sqrt(torch.sum(diffs_squared, dim=2))
    del diffs_squared
    # вычисляем среднее расстояние между точками
    avg_dist[d - 1] = torch.sum(distances_full).item() / dist_count
    # вычисляем расстояния до ближайших соседей точек
    distances_full[distances_full == 0.0] = np.sqrt(d) + 1
    distances_nn, _ = torch.min(distances_full, dim=0)
    del distances_full
    # вычисляем среднее расстояние до ближайшего соседа
    avg_dist_nn[d - 1] = torch.mean(distances_nn).item()
    del distances_nn

torch.cuda.empty_cache()

Тут мы используем гораздо меньшее количество точек, чем раньше, так как размер главной структуры данных увеличивается в соответствии с формулой N^2, а это значит, что, если сгенерировать слишком много точек, мы очень скоро столкнёмся с нехваткой памяти. Но даже так наши приблизительные результаты должны быть достаточно близки к реальным значениям.

Вот сводка по средним расстояниям между двумя точками, вычисленным для 1000 точек.

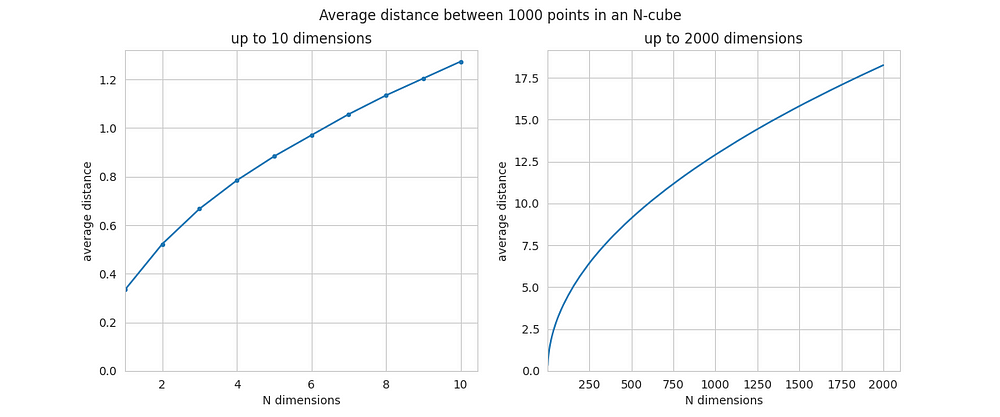
Для маленьких N среднее расстояние представлено числом от примерно 0,5 до примерно 1. Но по мере роста N растёт и среднее расстояние между точками. При N=2000 оно уже близко к 18. Это — серьёзный рост.

А вот — визуализация среднего расстояния до ближайшего соседа точки.

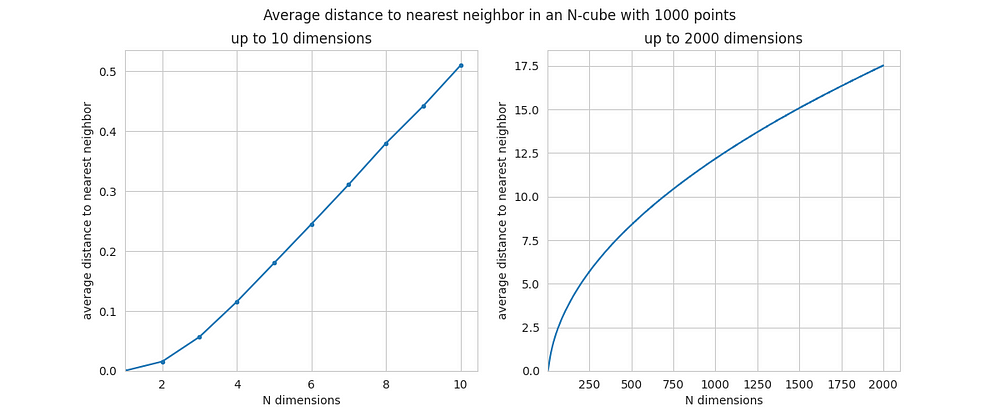
Тут рост N приводит к ещё более серьёзному росту расстояния, чем в предыдущем примере. Когда N меньше 10 — расстояния совсем невелики, так как в пространствах низкой размерности больше точек оказываются поблизости друг от друга. А для больших значений N среднее расстояние до ближайшего соседа оказывается очень близким к среднему расстоянию между любыми двумя точками. Другими словами, видно, что основной вклад в расстояние между точками вносит пустота, находящаяся в непосредственной близости от точек.

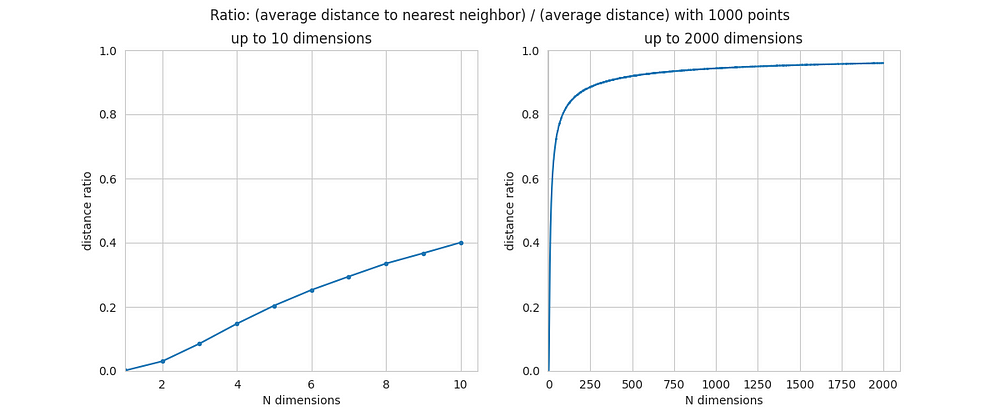
Именно поэтому выше было сказано, что в пространствах высокой размерности точки оказываются практически равноудалёнными друг от друга. Среднее расстояние между двумя точками и кратчайшее расстояние между точками оказываются практически одинаковыми. А теперь вы видите доказательство этого утверждения, полученное путём моделирования. Теперь вы можете ощутить мощь феномена проклятия размерности на интуитивном уровне.

По мере роста количества размерностей N точки всё дальше и дальше отходят друг от друга, несмотря на то, что их координаты ограничены одним и тем же, довольно узким диапазоном значений (-0,5, +0,5). Группа точек становится всё более и более разреженной только из‑за того, что пространство, в котором расположены эти точки, приобретает большее количество измерений. При увеличении количества размерностей с нескольких единиц до нескольких тысяч мы имеем дело с увеличением расстояния между точками на пару порядков. Это очень много.

Итоги

Проклятие размерности — это реальное явление, основанное на особенностях геометрии N‑мерных пространств.

По мере увеличения количества размерностей (или признаков) точки (наблюдения) быстро «убегают» друг от друга. В новом пространстве, определённо, больше места для размещения данных, несмотря даже на то, что линейные интервалы по осям остаются неизменными. Чем больше размерность пространства, в котором находятся точки, тем пустыннее окрестности этих точек.

В общем случае количество наблюдений должно «соответствовать» количеству признаков. Но в каждой конкретной ситуации желательное соотношение количества наблюдений и количества признаков зависит от множества факторов.

Надеюсь, эта статья дала вам ключ к интуитивному пониманию свойств многомерных пространств, которые очень сложно визуализировать. Некоторые описанные здесь тенденции, характеризующие то, что называют «проклятием размерности», удивительно сильны. Теперь у вас должно сложиться некоторое представление о том, насколько они сильны.

Репозиторий с кодом к статье