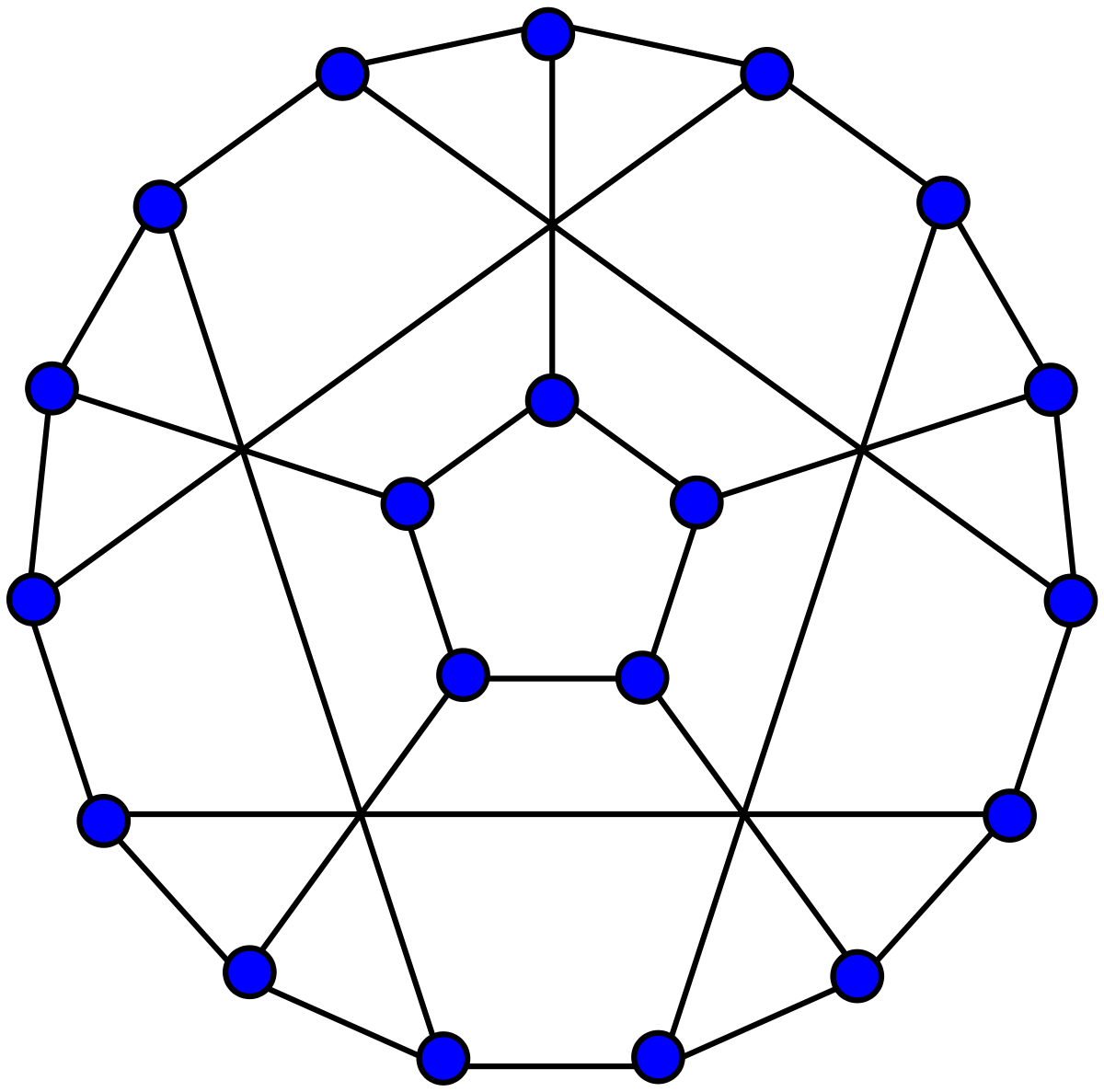
Всем привет! Меня зовут Нурислам (aka tonitaga), и сегодня я бы вам хотел рассказать об Базовых алгоритмах на графах.
Что такое граф?
Рассматриваемые алгоритмы
- Обход графа в ширину (Поиск в ширину) aka BFS | Breadth First Search
- Обход графа в глубину (Поиск в глубину) aka DFS | Depth First Search
- Алгоритм Дейкстры
- Алгоритм Флойда-Уоршелла
- Алгоритм Прима
Причина написания статьи
- Объединение базовых алгоритмов на графах в одну статью (понятно, что для каждого базовые алгоритмы на графах это свое, но я выделил те, которые сам считаю базовыми)
Представление графа в коде
- Представим граф в виде класса обёртки над матрицей смежности. Класс-wrapper будет знать количество рёбер, вершин, и тип графа. Обычно такого функционала хватает для большинства алгоритмов.
BFS & DFS
Поиск (Обход) в ширину | BFS
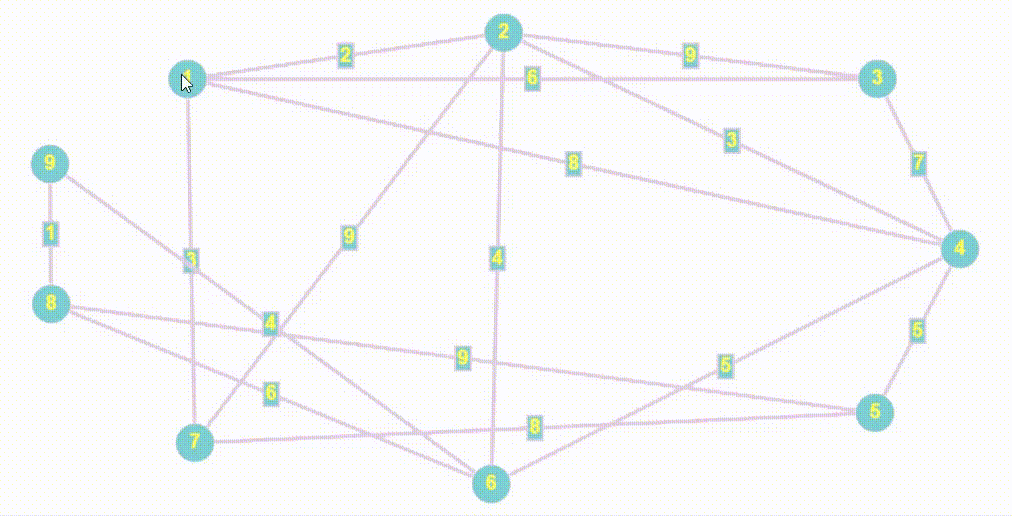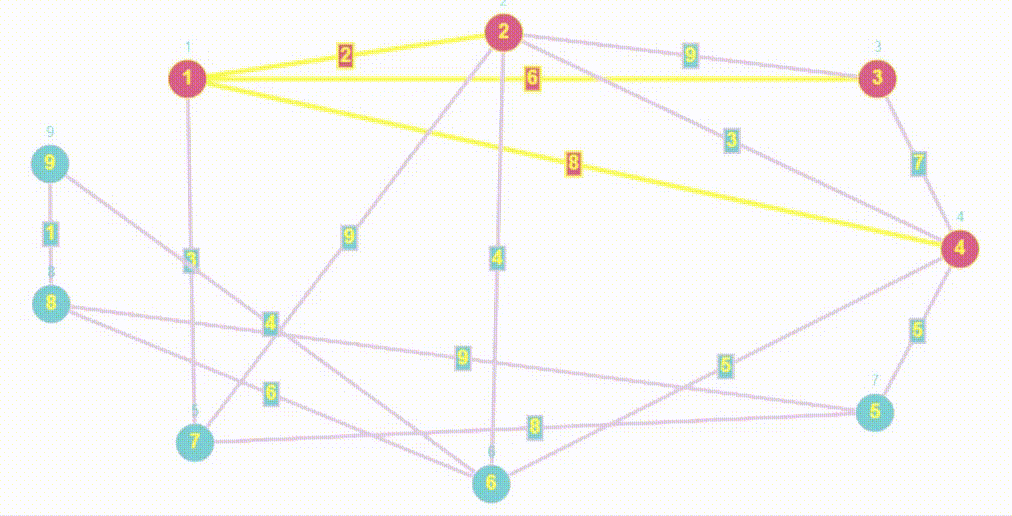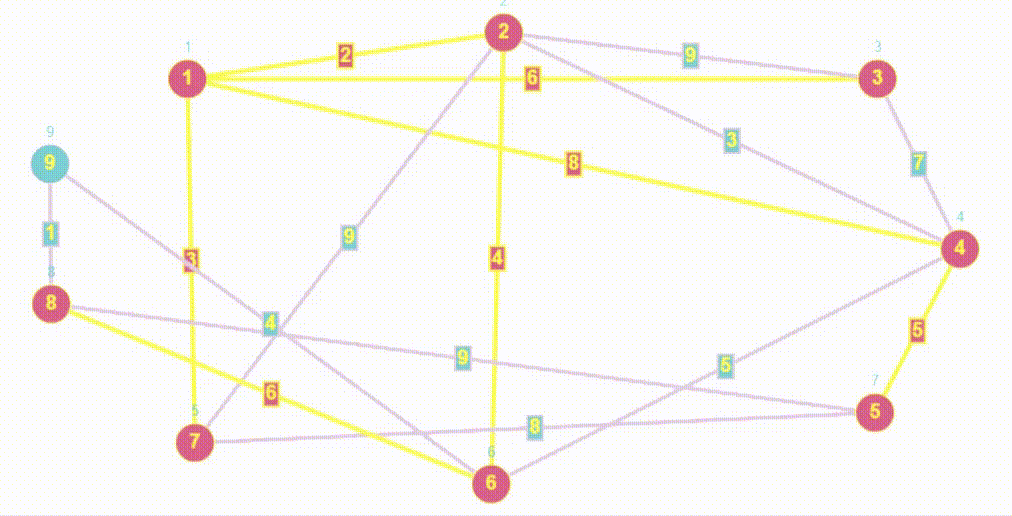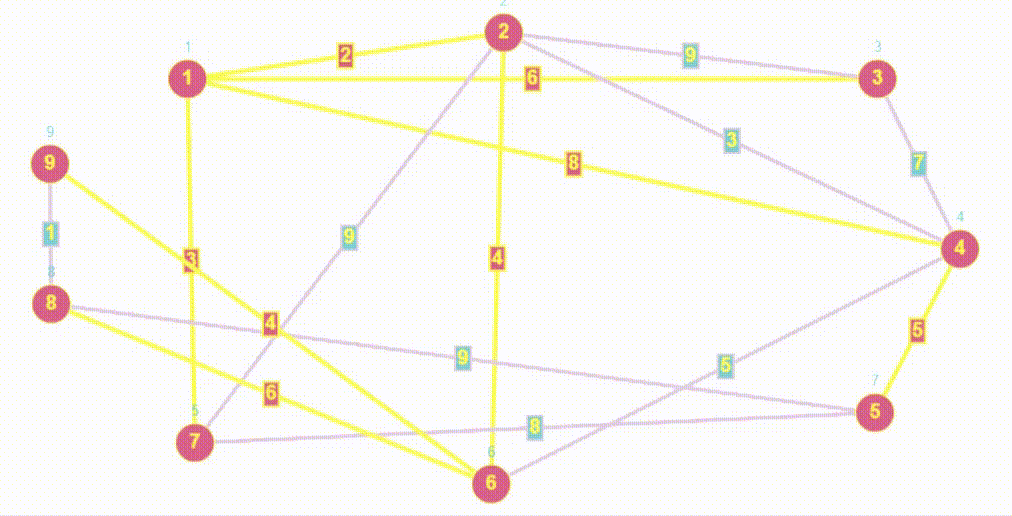
- BFS (breadth first search) — это алгоритм, используемый для обхода или поиска в графах и деревьях. Он начинается с выбранной вершины и обходит сначала все доступные вершины на текущем уровне перед переходом на следующий уровень.
- Алгоритм BFS очень похож на Волновой алгоритм, так как волновой алгоритм относится к семейству алгоритмов основанных на методах поиска в ширину.
- Обход в ширину работает на основе очереди
- Сложность алгоритма обхода в ширину является линейной и равна O(V+E), где V — количество вершин графа, E — количество ребер в графе.
Алгоритм
- На вход в функцию BFS приходит граф и стартовая вершина
- Возвращать BFS будет массив порядка посещения вершин (пометим как enter_order)
- Помечаем стартовую вершину как посещенную (в дальнейшем нам это понадобится)
- Кладем в очередь нашу стартовую вершину и кладем в enter_order нашу стартовую вершину
- Пока наша очередь
5.1. Получаем элемент из очереди (пометим это как from) (в очереди хранится лишь порядковый номер вершины)
5.2. Удаляем вытащенный элемент из очереди
5.3. Перебирая все вершины графа:
5.3.1. Если перебираемая вершина (пометим как to) непосещенная и по матрице смежности между from и to есть ребро, то
5.3.1.1. Помечает вершину to как посещенную
5.3.1.2. Кладем эту вершину в очередь и enter_order
5.3.2. Иначе ничего не делаем - Возвращаем enter_order
Поиск (Обход) в глубину| DFS

- DFS (depth first search) — это алгоритм, используемый для обхода или поиска в графах и деревьях. Он начинается с выбранной вершины и обходит все доступные вершины на максимальную глубину, прежде чем возвращаться к следующей непосещенной вершине.
- Основное отличие BFS от DFS только в том, что BFS используется очередь а DFS используется stack, в остальном алгоритм обхода практически не отличается
- Обычно все реализовывают рекурсивный обход в глубину, я распишу алгоритм итеративного обхода в глубину
- Сложность алгоритма обхода в глубину такая же как и у BFS алгоритма, и равна O(V+E), где V — количество вершин графа, E — количество ребер в графе.
Алгоритм
- На вход в функция DFS приходит граф и стартовая вершина
- Возвращать BFS будет массив порядка посещения вершин (пометим как enter_order)
- Помечаем стартовую вершину как посещенную (в дальнейшем нам это понадобится)
- Кладем в стек нашу стартовую вершину и кладем в enter_order нашу стартовую вершину
- Пока наш стек не пустой:
5.1. Получаем элемент из стека (пометим это как from)
5.2. Перебирая все вершины графа:
5.2.1. Если перебираемая вершина (пометим как to) непосещенная и по матрице смежности между from и to есть ребро, то
5.2.1.1. Помечаем вершину to как посещенную
5.2.1.2. Кладем эту вершину в стек и в enter_order
5.2.1.3. Присваиваем вершине from значение вершины to (Это нужно для того чтобы просматривать ребра в глубину)
5.2.2. Иначе ничего не делаем
5.3. Если условие 5.2.1 не выполнилось выполнилось, то удаляем из стека наш верхний элемент - Возвращаем enter_order
BFS
std::vector<int> BreadthFirstSearch(Graph &graph, int start_vertex) {
if (start_vertex > graph.GetVertexesCount() or start_vertex <= 0)
return {};
std::vector<int> enter_order;
std::vector<short> visited(graph.GetVertexesCount());
std::queue<int> q;
// Функция принимает вершину, нумерация которой начинается с 1
// Для удобства уменьшаем ее значение на 1, чтобы нумерация начиналась с 0
--start_vertex;
visited[start_vertex] = true;
q.push(start_vertex);
enter_order.emplace_back(start_vertex + 1);
while (!q.empty()) {
auto from = q.front();
q.pop();
for (int to = 0, size = graph.GetVertexesCount(); to != size; ++to) {
if (!visited[to] and graph(from, to) != 0) {
visited[to] = true;
q.push(to);
enter_order.emplace_back(to + 1);
}
}
}
return enter_order;
}DFS
std::vector<int> DepthFirstSearch(Graph &graph, int start_vertex) {
if (start_vertex > graph.GetVertexesCount() or start_vertex <= 0)
return {};
std::vector<int> enter_order;
std::vector<short> visited(graph.GetVertexesCount());
std::stack<int> s;
--start_vertex;
visited[start_vertex] = true;
s.push(start_vertex);
enter_order.emplace_back(start_vertex + 1);
while (!s.empty()) {
auto from = c.top();
bool is_found = false;
for (int to = 0, size = graph.GetVertexesCount(); to != size; ++to) {
if (!visited[to] and graph(from, to) != 0) {
is_found = true;
visited[to] = true;
s.push(to);
enter_order.emplace_back(to + 1);
from = to;
}
}
if (!is_found)
s.pop();
}
return enter_order;
}Заметим, что код практически ничем не отличается, поэтому их можно объединить в одну функцию, и передавать туда просто тип контейнера
//
// If Container type = std::stack<int> it will be DepthFirstSearch
// If Container type = std::queue<int> it will be BreadthFirstSearch
//
template <typename Container = std::stack<int>>
std::vector<int> FirstSearch(Graph &graph, int start_vertex)
{
if (start_vertex > graph.GetVertexesCount() or start_vertex <= 0)
return {};
constexpr bool is_stack = std::is_same_v<Container, std::stack<int>>;
std::vector<int> enter_order;
std::vector<short> visited(graph.GetVertexesCount());
Container c;
--start_vertex;
visited[start_vertex] = true;
c.push(start_vertex);
enter_order.emplace_back(start_vertex + 1);
while (!c.empty()) {
int from = -1;
if constexpr (is_stack) from = c.top();
else {
from = c.front();
c.pop()
}
bool is_found = false;
for (int to = 0, size = graph.GetVertexesCount(); to != size; ++to) {
if (!visited[to] and graph(from, to) != 0) {
is_found = true;
visited[to] = true;
c.push(to);
enter_order.emplace_back(to + 1);
if (is_stack)
from = to;
}
}
if (is_stack and !is_found)
c.pop();
}
return enter_order;
}- Тогда код BFS & DFS будет выглядеть так:
std::vector<int> BreadthFirstSearch(Graph &graph, int start_vertex) {
return FirstSearch<std::queue<int>>(graph, start_vertex);
}
std::vector<int> DepthFirstSearch(Graph &graph, int start_vertex) {
return FirstSearch<std::stack<int>>(graph, start_vertex);
}Алгоритм Дейкстры
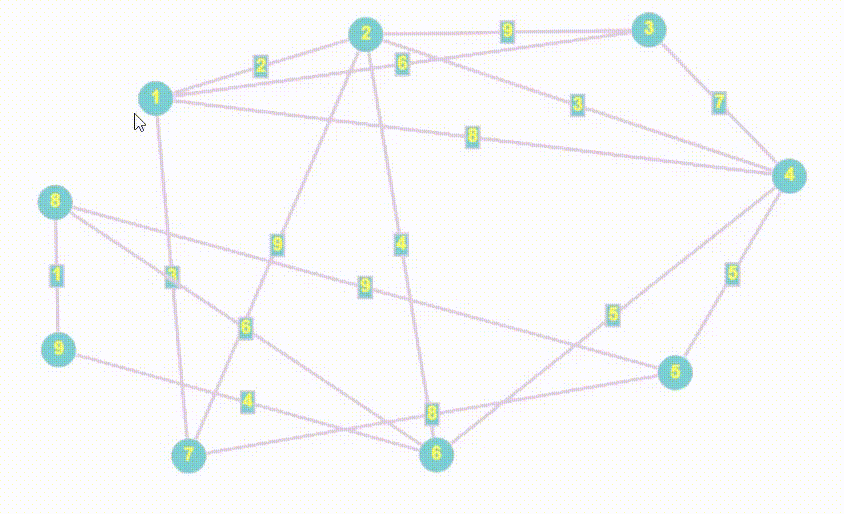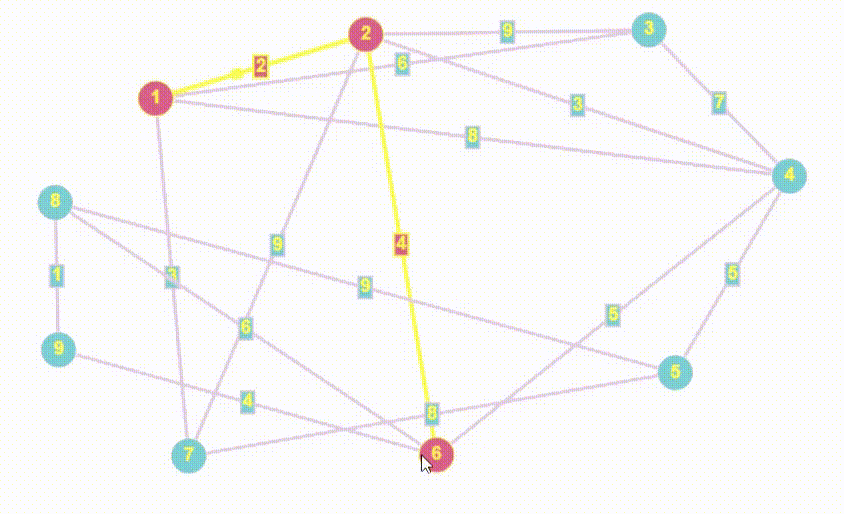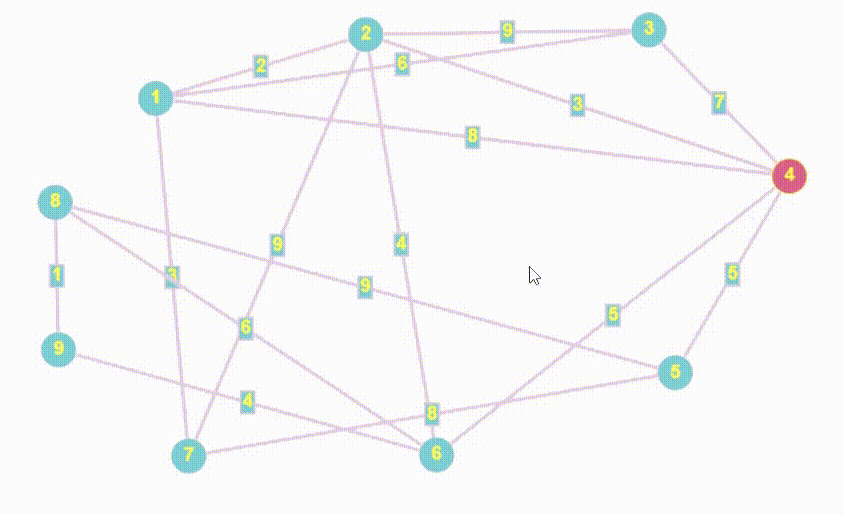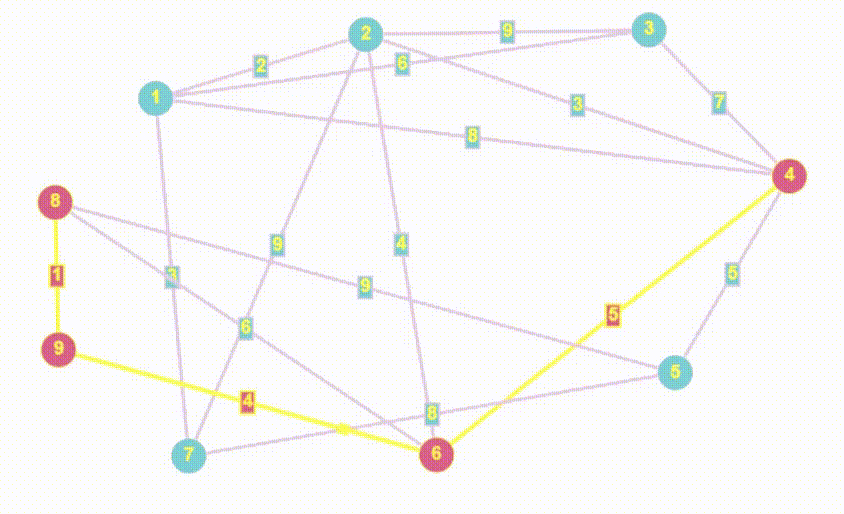
- Алгоритм Дейкстры — это алгоритм нахождения кратчайшего пути от одной вершины графа до всех остальных вершин. Он работает только с неотрицательными весами ребер и является одним из самых эффективных алгоритмов для нахождения кратчайших путей в графах.
- Алгоритм Дейкстры принципом работы очень похож на BFS
- Полный алгоритм Дейкстры возвращает массив кратчайших расстояний от стартовой точки до всех остальных, мы найдем все расстояния, но вернем лишь то, которое хочет пользователь
- Единственным минусом алгоритма Дейкстры являемся, неумение работать с отрицательными весами ребер
- Сложность Алгоритма Дейкстры растет линейно-логарифмически и равна O(ЕlogV), где V — количество вершин графа, E — количество ребер графа. Такая сложность делает его эффективным при работе с большими графами.
- Основным применением является нахождение кратчайшего пути между двумя вершинами графа. Он может быть использован в сетевых задачах, таких как определение оптимального пути для передачи данных по сети или для оптимизации маршрутов в GPS-навигации.
Алгоритм
- На вход функция Алгоритма Дейкстры будет принимать граф и две вершины, стартовая (пометим как start) и конечная (пометим как finish)
- Создадим массив длин от start до всех остальных вершин (пометим как distance), изначально пометим все длины в массиве бесконечностью.
- Стартовую точку в distance пометим как 0, потому что расстояние от точки, до самой точки равно нулю (в данном алгоритме мы не рассматриваем ситуации когда есть петли)
- Создаем множество из пары значений, пара будет хранить длину и индекс вершины
- Инициализируем наше множество стартовым значением, за стартовое значение отвечает стартовая вершина, поэтому в множестве будет лежать: длина -> 0 и индекс start
- Пока наше множество не пусто:
6.1. Получаем начальный элемент в множестве (пометим как from) (вспоминаем, что в множестве хранится пара значений, нам нужен лишь индекс вершины)
6.2. Удаляем начальный элемент из множества
6.3. Перебирая все вершины графа:
6.3.1. Если между from и перебираемой вершиной (пометим как to) есть ребро
6.3.2. И если расстояние от start до to больше чем расстояние от start до from + вес самого ребра (from, to)
6.3.2.1. Удаляем из множества старую пару значений: {расстояние от start до to, индекс вершины to}
6.3.2.2. В distance обновляем расстояние от start до to на более короткое, которое мы проверяли в условии 6.3.2
6.3.2.3. Вставляем в множество обновленную пару: {расстояние от start до to, индекс вершины to} - Возвращаем из массива distance расстояние под индексом finish
int GetShortestPathBetweenVertices(Graph &graph, int start, int finish) {
if (start <= 0 or finish <= 0 or start > graph.GetVertexesCount() or finish > graph.GetVertexesCount())
return kInf;
std::vector<int> distance(graph.GetVertexesCount(), kInf);
--start, --finish;
distance[start] = 0;
std::set<std::pair<int, int>> q;
q.insert({distance[start], start});
while (!q.empty()) {
auto from = q.begin()->second;
q.erase(q.begin());
for (int to = 0, size = graph.GetVertexesCount(); to != size; ++to) {
bool edge_is_exists = graph(from, to) != 0;
bool new_edge_is_shorter = distance[to] > distance[from] + graph(from, to);
if (edge_is_exists and new_edge_is_shorter) {
q.erase({distance[to], to});
distance[to] = distance[from] + graph(from, to);
q.insert({distance[to], to});
}
}
}
return distance[finish];
}По коду можно увидеть явные признаки схожести с BFS, я даже специально множество назвал как q, потому что в данном случае множество отыгрывает роль псевдо-очереди
Алгоритм Флойда-Уоршелла

- Алгоритм Флойда-Уоршелла — это алгоритм поиска кратчайших путей во взвешенном и не взвешенном графе с положительным или отрицательным весом ребер (но без отрицательных циклов). За одно выполнение алгоритма будут найдены длины (суммарные веса) кратчайших путей между всеми парами вершин.
- Логично что алгоритм будет возвращать матрицу расстояний между всеми парами вершин (грубо говоря новую матрицу смежности)
- Алгоритм не содержит детали о самих кратчайших путях, а запоминает лишь кратчайшее расстояние, но алгоритм можно усовершенствовать, ссылка на видео здесь, да и описание вместе с реализацией можно посмотреть там же.
- Сложность Алгоритма Флойда-Уоршелла независимо от типа графа O(V^3), где V — количество вершин.
- Можно сказать что алгоритм Флойда-Уоршелла делает тоже самое, что и алгоритм Дейкстры, только находит кратчайшие расстояния не только между двумя вершинами, а всеми сразу.
Алгоритм
- На вход функция Алгоритма Флойда-Уоршелла будет принимать только сам граф
- Создаем копию матрицы смежности графа (пометим как distance)
2.1. Основное отличие distance от той, которая лежит в графе лишь в том, что все нули в матрице смежности графа, в матрице distance будут бесконечностью (кроме главной диагонали), так как главная диагональ хранит в себе расстояние от вершины до самой себя, поэтому и ноль (мы не учитываем ситуации с петлями, предположим что их нет) - Постепенно открывая доступ к вершинам (открытие доступа к вершине означает, что мы просто перебираем все вершины с индексами от 0 до V — 1 (конечно же, если индексация нулевая)), пусть вершина, к которой открыли доступ называется v:
3.1. Просматривая все возможные и невозможные ребра в графе (в двух циклах пробегаемся по матрице distance), пусть счетчик внешнего цикла будет называться row, а счетчик вложенного цикла будет называться col:
3.1.1. Получаем суммарный вес ребер {row, v} и {v, col}
3.1.2. Если ребро {row, v} и ребро {v, col} существуют и текущее значение в матрице distance под индексами {row, col} больше чем суммарный вес двух новых ребер, то:
3.1.2.1. Обновляем в матрице distance расстояние на более короткое, которое мы вычислили в пункте 3.1.1
3.1.3. Иначе ничего не делаем - Возвращаем матрицу distance

Matrix<int> GetShortestPathsBetweenAllVertices(Graph &graph) {
const int vertexes_count = graph.GetVertexesCount();
Matrix<int> distance(vertexes_count, vertexes_count, kInf);
// Пункт 2
for (int row = 0; row != vertexes_count; ++row) {
for (int col = 0; col != vertexes_count; ++col) {
distance(row, col) = graph(row, col) == 0 ? kInf : graph(row, col);
if (row == col)
distance(row, col) = 0;
}
}
// Пункт 3 (Постепенно открываем доступ к новым вершинам)
for (int v = 0; v != vertexes_count; ++v) {
// Пункт 3.1 (Пробегаемся по матрице distance)
for (std::size_t row = 0; row != vertexes_count; ++row) {
for (std::size_t col = 0; col != vertexes_count; ++col) {
int weight = distance(row, v) + distance(v, col);
if (distance(row, v) != kInf and distance(v, col) != kInf and distance(row, col) > weight)
distance(row, col) = weight;
}
}
}
return distance;
}Написать реализацию гораздо проще, чем понять как этот алгоритм работаем, поэтому советую ознакомиться с видео
Алгоритм Прима
- Алгоритм Прима — это алгоритм нахождения минимального остовного дерева (MST) в связном взвешенном графе. Он начинает с выбранной стартовой вершины и постепенно добавляет ребра с наименьшим весом, чтобы связать все вершины графа.
- Алгоритм Прима работает с неориентированными графами, поэтому если нам был передам ориентированный граф, мы будем игнорировать направление ребер.
- Сложность Алгоритма Прима растет логарифмически и равна O(ElogV), где V — количество вершин графа, E — количество ребер в графе.
- Остовное дерево должно включать в себя все вершины графа
- Каждая вершина должна быть посещена ровно 1 раз
- Результатом работы Алгоритма прима будет матрица смежности дерева
Скажу сразу, что моя реализация не умеет работать с графами у которых, есть изолированные вершины, как только я это сделаю я изменю статью, спасибо за понимание.
Алгоритм
- Создаем два множеств, для посещенных и не посещенных вершин (пометим, соответственно, как visited и unvisited)
- Создаем исходную матрицу, которая будет представлять собой остовное дерево (пометим как spanning_tree)
- Создаем массив ребер (пометим как tree_edges), ребро в данном случае это структура, которая хранит две вершины и вес самого ребра.
- Инициализируем множество непосещенных вершин всеми, существующими в графе вершинами
- Выбираем, случайным образом, вершину, от которой будет строиться остовное дерево, и помечаем эту вершину как посещенной, соответственно из множества непосещенных ее убираем
- Пока множество непосещенных першин не пусто:
6.1. Создаем ребро инициализируя его поля бесконечностями
6.2. Перебирая все посещенные вершины (пометим как from):
6.2.1. Перебираем все вершины графа (пометим как to):
6.2.1.1. Если to является непосещенной вершиной и ребро между вершинами {from, to} существует и вес ребра (созданного в пункте 5.1) больше чем вес ребра между вершинами {from, to}, то:
6.2.1.1.1. Обновляем ребро (5.1) вершинами from и to и весом между этими вершинами
6.3. Если вес ребра не равен бесконечности:
6.3.1. Добавляем в массив tree_edges новое ребро
6.3.2. Удаляем из множества непосещенных вершин вершину to
6.3.3. Добавляем в множество посещенных вершин вершину to
6.3.4. Иначе прекращаем цикл - Пробегаясь по всем ребрам массива tree_edges:
7.1. Инициализируем spanning_tree, добавляя в нее ребра (добавлять нужно в обе стороны, чтобы граф получился неориентированным) - Возвращаем spanning_tree
Matrix<int> GraphAlgorithms::GetLeastSpanningTree(Graph &graph) {
const auto vertexes_count = graph.GetVertexesCount();
Matrix<int> spanning_tree(vertexes_count, vertexes_count, kInf);
std::set<int> visited, unvisited;
std::vector<Edge> tree_edges;
for (int v = 0; v != vertexes_count; ++v)
unvisited.insert(v);
{
// Вершина должна браться случайно, но какая разница, если дерево статичное.
// Дерево независимо от start_vertex всегда одинаковое
const auto start_vertex = static_cast<int>(vertexes_count / 2);
visited.insert(start_vertex);
unvisited.erase(start_vertex);
}
// Initialize Finish -> Start main loop
while (!unvisited.empty()) {
Edge edge(kInf, kInf, kInf);
for (const auto &from : visited) {
for (int to = 0; to != vertexes_count; ++to) {
bool is_unvisited_vertex = unvisited.find(to) != unvisited.end();
bool edge_is_exists = graph(from, to) != 0 or graph(to, from) != 0;
if (edge_is_exists and is_unvisited_vertex) {
int existed_weight = graph(from, to) == 0 ? graph(to, from) : graph(from, to);
bool edge_is_shorter = edge.weight > existed_weight;
if (edge_is_shorter)
edge = {from, to, existed_weight};
}
}
}
if (edge.weight != kInf) {
tree_edges.emplace_back(edge);
visited.insert(edge.vertex2);
unvisited.erase(edge.vertex2);
} else {
break;
}
}
// Initializing spanning tree
for (const auto &edge : tree_edges) {
spanning_tree(edge.vertex1, edge.vertex2) = edge.weight;
spanning_tree(edge.vertex2, edge.vertex1) = edge.weight;
}
return spanning_tree;
}Для чего используют эти алгоритмы?
BFS
- Алгоритм BFS используется для решения задач поиска оптимального пути. Одной из таких задач считается поиск выхода из лабиринта.
- Для задач искусственного интеллекта, связанных с поиском решения с минимальным количеством ходов. В таком случае состояния «умной машины» представляются как вершины, а переходы между ними — как ребра.
- Конечно, еще не мало примеров, где используется BFS, но я привел пару примеров.
DFS
- Также как и алгоритм BFS, DFS может быть использован для нахождения пути в лабиринте, однако DFS используется для поиска произвольного маршрута в лабиринте. BFS ищет оптимальный путь в лабиринте, а DFS ищет не всегда самый короткий (исключая ситуации, когда в лабиринте между двумя точками единственный путь).
- Пример использования DFS вне программирования: Правило прохождения лабиринта, придерживаясь правила левой руки, ну либо правой руки.
- Алгоритм DFS используется для нахождения циклов в графе.
Алгоритм Дейкстры
- Основное использование Алгоритма Дейкстры — это оптимальный (кратчайший) маршрут между двумя произвольными точками. Например прокладывание оптимального маршрута между двумя точками на карте или сети дорог.
- Алгоритм Дейкстры может использоваться для оптимизации расписания задач. Например, у нас есть поставленные задачи, ограниченный по времени, также каждая задача может иметь определенные зависимости от других задач. При использовании данного Алгоритма, можно составить оптимальный порядок выполнения данных задач, для сокращения суммарного времени выполнения всех задач.
Алгоритм Флойда-Уоршелла
- Алгоритм Флойда-Уоршелла может быть использован для оптимизации транспортных сетей. Например, есть какая-то транспортная сеть, где разные дороги имеют различные время путешествия. Алгоритм Флойда-Уоршелла поможет найти наиболее эффективные пути между всеми парами городов. Это может быть использовано для оптимизации грузоперевозок, или для улучшения времени обхода общественного транспорта.
Алгоритм Прима
- Напомню, что Алгоритм Прима используется для нахождения остовного дерева в графе с минимальным весом. Это может быть использовано для определения оптимального маршрута коммуникационной сети. Например, возьмем газопровод соединяющий города, для того чтобы использовать минимальное количество материала для изготовления труб газопровода, используется Алгоритм Прима, чтобы соединить эти города сетью газопровода, максимально выгодным образом.
Плюсы и минусы
BFS
Плюсы:
- Простота реализации, так как BFS является одним из наиболее простых алгоритмов обхода графа.
- Удобство нахождения связанных компонентов, так как BFS сначала перебирает все доступные вершины и только потом переходит на следующий уровень, то таким образом можно найти всё вершины достижимые от заданной точки.
- Гарантирует нахождения кратчайшего пути в невзвешенном графе.
Минусы:
- Требует дополнительную память, так как нужно хранить порядок обхода вершин. Соответсвенно алгоритм требует по памяти О(V), где V — количество вершин в графе.
- Алгоритм бесполезен для графов с отрицательными весами, там как BFS не учитывает вес ребра.
- Не способен генерировать оптимальный путь для взвешенных графов. Путь может быть найден, но не факт, что он будет оптимальным.
DFS
Плюсы:
- Простота реализации независимо от типа способа, на стеке или при помощи рекурсии.
- Эффективность, иногда DFS более предпочтителен нежели BFS, когда дело заходит о достижении определённой вершины
Минусы:
- Также как и BFS требует доп памяти О(V)
- Нет гарантии нахождения кратчайшего пути в невзвешенном графе
- Склонность к зацикливание, если у графа есть циклы
Алгоритм Дейкстры
Плюсы:
- Эффективность, сложность алгоритма линейно-логарифмическая, что делает этот алгоритм эффективным на больших графах.
- Гарантия оптимальности. Алгоритм Дейкстры гарантирует нахождение кратчайших расстояний от стартовой до всех остальных.
Минусы:
- Требует положительный вес ребер. Почему?
- Требует полной информации о графе, количество вершин, вес рёбер должен быть известен.
Алгоритм Флойда-Уоршелла
Плюсы:
- Гарантия нахождения кратчайших расстояний между всеми парами вершин.
- Эффективность для небольших графах
Минусы:
- Высокая сложность О(V^3).
- Неэффективность на больших графах, с большим количеством вершин.
- Дополнительная память, в виде матрицы {V, V}, что также для больших графов может быть критично.
Алгоритм Прима
Плюсы:
- Гарантия нахождения минимального основного дерева для неориентированных графов
- Высокая эффективность для разреженных графов, когда количество рёбер меньше количества вершин. Это связано с тем, что алгоритм работает только с непосещенными ребрами.
Минусы:
- Неэффективность для плотных графов, так как алгоритм Прима анализирует рёбра, то количество рёбер близкое к максимально возможным делают этот алгоритм неэффективным.
- Дополнительная память О(V^2), что для графов с большим количество вершим может быть критично.
Полезные ссылки
- Сайт, где можно проверить работу своего алгоритма: графы.
- Хочу поделиться своим github'ом, буду признателен если вы оформите подписку: GitHub.
- Ссылка на youtube канал, с описанием этих и других алгоритмов на графах.
Комментарии (39)

anonymous
03.08.2023 14:25НЛО прилетело и опубликовало эту надпись здесь

tonitaga Автор
03.08.2023 14:25+3Матрица смежности это один из вариантов представления графа в памяти компьютера. Есть и другие способы, но простой обёртки, которая знает количество рёбер, вершин и тип графа, достаточно для большинства задач, можешь ознакомиться с этой обёрткой у меня на github'e "GraphAlgorithms"

WASD1
03.08.2023 14:25Но вы же действительно перепутали "граф" и "техническую реализацию" графа.

tonitaga Автор
03.08.2023 14:25Ничего не было перепутано, просто заголовки читать надо, заголовок, перед упоминанием обертки матрицы смежности, такой "Представление графа в коде"

WASD1
03.08.2023 14:25-1Что ж если продолжаете упорствовать в совём заблуждении:
представление графа в коде
Графом будет называться простая обертка над ххх
Это ошибка. Не "графом будет называться обёртка над ххх", а "граф будет реализован как обёртка над ххх" - ну за исключением случаев когда вы граф зачем-то определяете не так, как общепринято.
просто заголовки читать надо
Наличие какого угодно заголовка не даёт индульгенции от фактических ошибок.
Итог (пока предварительный):
Статья не рекомендуется к прочтению потому, что:
1. статья содержит ошибки (что снижает её качество).
2. После указания на фактические ошибки автор вместо исправления их и улучшения статьи пытается выкрутиться чтобы их не исправлять.

capjdcoder
03.08.2023 14:25+5Графом будет называться простая обертка над матрицей смежности
Автор, дайте нормальное определение графу и не вводите людей в заблуждение.
Граф
— это пара множеств
где
— непустое конечное множество элементов, называемых вершинами графа, а
— множество пар элементов из
(необязательно различных), называемых ребрами графа.
То что вы написали является всего лишь одним из видов записи или представления графа в компьютерных науках. Другими способами записать граф являются:
лист смежности (adjacency list)
лист вершин (Edge list)
матрица инцидентности (Incidence Matrix)
Compressed Sparse Column или Compressed Sparse Row (обычно для больших разреженных графов)
Каждый из указанных методов имеет свои достоинства и недостатки.
Делать такое однозначное утвеждение, что "Графом будет называться простая обертка над матрицей смежности" - простите, но это либо верх неуважения к аудитории либо банальное невежество.
Уж простите, не смог пройти мимо и не поправить.

GospodinKolhoznik
03.08.2023 14:25-2Просто хочу немного подискутировать: Как мне кажется, граф это неопределяемое понятие, понимаемое на уровне интуиции. Ну т.е. определение то есть, но если подумать, оно определяет само через себя.
Точно так же как и функция. На примере функции проще объяснить. Что такое функция? По определению это правило, которое ставит элементу множества X элемент из множества Y, обладающее свойствами... А что такое правило? Ну это же синоним слову функция. Просто игра слов. Ок. Есть другое определение слову функция - это подмножество из множества декартового произведения XxY, обладающее свойствами... (Очень похоже на ваше определение графа. Ну и это понятно, ведь с помощью графа можно определить функцию). Но подождите, мы же ничего по сути не поменяли. Было - функция это правило сопоставления элементов... Стало - функция это правило по которому из множества декартовых произведений выбирается подмножество... Опять все упирается в правило, которое является синонимом самому слову функция.
Что касается вашего определения графа, это правило, по которому выбирается подмножество из декартового произведения VxV. А правило это по сути некоторая функция, а функция может быть определена с помощью графа. Круг замкнулся.

thevlad
03.08.2023 14:25+3Даже не знаю что и сказать, почитайте основы мат. логики и теории множеств, там все описано. Функция это подмножество декартового произведения, как вы его выберете? Ну можно предикат определить, или просто перечислить все элементы если множество конечное.
И в случаи графа дуги это именно конечное множество упорядоченных(или нет, если граф не направленный) пар вершин, это множество конечное, и его можно просто перечислить. Все просто.
И автор комментария правильно написал, что представления графов множества, и чаще всего матрица смежности далеко не самое эффективное.

GospodinKolhoznik
03.08.2023 14:25Хм это я не знаю что сказать. Вы предлагаете использовать предикат, чтобы определить подмножество, которое определяет функцию. Но предикат это и есть функция.
И вы мне ещё будете советовать читать основы мат. логики и теории множеств... Вам не показалось, что я их достаточно хорошо знаю, если вижу потенциальную проблему в определении графа?

dgoncharov
03.08.2023 14:25Извините, но у вас и правда рассуждения немного "не в кассу". ИМХО, определение графа через множества вершин и ребер одновременно и строгое, и интуитивно понятное. Вы говорите, что множество ребер графа может быть задано как логическая функция от VxV. ОК, пожалуйста. В этом нет никакого противоречия.
А что такое правило? Ну это же синоним слову функция.
Что такое функция? По определению это правило, <...> обладающее свойствами...
Вообще-то это оффтопик, тут не про функции разговор, а про графы, но ладно. Почему вдруг синоним? Не любое правило есть функция, так что это уж точно не синонимы. "А есть такое Б, которое обладает свойством С" - типичное логическое определение. Это вовсе не тавтология. А определяется не "само через себя", а через Б и С.
ведь с помощью графа можно определить функцию
Ну это ваше собственное заявление, никто тут такого не говорил. Далеко не любую функцию можно определить через граф.

GospodinKolhoznik
03.08.2023 14:25Если рассуждения "не в кассу", прошу извинить. Я сразу написал, что предлагаю подискутировать на тему сложности определения термина граф, раз уж автору тыкнули, что он определяет граф как то не так, как принято. Чтобы те, кто не хочет дискутировать, не обращали внимание. Ну а моё мнение, что такого рода сущности не могут быть никак определены, так же как невозможно определить что такое точка, прямая и плоскость. Ну и что такое функция тоже невозможно определить, поэтому я много написал про функцию, т.к. граф и функция взаимно эквивалентны и могут быть выведены один из другого. Ну т.е. определения то у них есть. Но это такие определения-заглушки, нужные для педагогического процесса, чтобы студенты не смущались от того, что опереируют неопределяемыми терминами, для них придумали определение термина через себя самого, но сделали это завуалированно, чтобы было незаметно.
Функция и правило не синонимы. Ну пусть не синонимы. Но тогда неплохо бы определить что такое правило, а не подменять один термин другим, у которого нет определения. Можно говорить, что функция это правило, отображение, мэппинг, способ сопоставления и т.п. но по сути это игра слов и подмена одного загадочного термина на другой.
И почему это не любую функцию можно определить через граф? Можете привести пример такой функции? Как я вижу, если есть f: X -> Y, то её можно определить как граф, где каждое ребро соединяет x и f(x).

dgoncharov
03.08.2023 14:25Ну подискутировать я и сам рад, только чтобы была связь с исходной темой, а то будем смешно выглядеть тут.
По-моему, то, что не любую функцию можно задать графом, совершенно очевидно даже школьнику. Вам нужен пример? Пожалуйста: f(x) = x^2. Да и вообще любая функция, определенная на множестве действительных чисел. (Про комплексные даже и не заикаюсь.)
Теперь по поводу определений и аксиоматических понятий. Вы правы в том, что не все определения логически строги. Но эта нестрогость, как ни странно, добавляет им смысла. А рекурсивное "разложение на атомы" какого-либо понятия вплоть до самых аксиом как раз смысл и отнимает. Потому что смысл понятий заключен не столько в их определениях, сколько в их связях и соотношениях с другими понятиями.Раз мы тут про графы говорим, то ваш поход предполагает, что связи между понятиями образуют направленный ациклический граф, который можно отсортировать топологической сортировкой от высоких уровней абстракции к низким. Но эти взаимосвязи, вероятно, все-таки образуют более сложную структуру.

GospodinKolhoznik
03.08.2023 14:25Не понимаю в чем проблема построить граф соответствующий функции f(x) = x^2 ? Просто каждую точку х соединить ребром с точкой x^2.
Более строго: G=(V,E) где V = R, E = подмножество из RxR, такое что второй элемент пары равен квадрату первого элемента.

dgoncharov
03.08.2023 14:25Не понимаю в чем проблема построить граф
Ну вот мне прямо интересно даже стало. Раз нет проблем, то постройте, пожалуйста. Мне очень интересно, как вы каждую точку бесконечного множества будете ребрами соединять с чем-то еще. Я хотел бы это увидеть на чертеже. Или в виде матрицы смежности. Или любой другой вышеупомянутой структуры данных.

GospodinKolhoznik
03.08.2023 14:25Ну как бы далеко не каждый граф можно изобразить на чертеже. Очевидно, что если множество ребер графа более чем конечно, то отобразить его на рисунке или запихать целиком в память ЭВМ несколько затруднительно. Просто в таких случаях граф задается аналитически.

dgoncharov
03.08.2023 14:25-1Более строго: G=(V,E) где V = R, E = подмножество из RxR, такое что второй элемент пары равен квадрату первого элемента.
Вы вот это называете "аналитическим заданием графа"? О, я так могу очень многое "аналитически позадавать". Вот например, сейчас "задам" четырехугольник с числом углов n=5. Разве кто-то может запретить четырехугольнику приобрести еще один угол?
Да, кстати, а почему "далеко не каждый граф можно изобразить на чертеже"? Бумаги не хватает?

thevlad
03.08.2023 14:25+2Вы предлагаете использовать предикат, чтобы определить подмножество, которое определяет функцию. Но предикат это и есть функция.
https://en.wikipedia.org/wiki/Predicate_(mathematical_logic)
И вы мне ещё будете советовать читать основы мат. логики и теории
множеств... Вам не показалось, что я их достаточно хорошо знаю, если
вижу потенциальную проблему в определении графа?Там нет проблем, есть ваше не понимание основ предмета, которому уже сотня лет стукнет. Типичный пример Даннинга - Крюгера: мало что понимаю в вопросе, но свое мнение выскажу.

dgoncharov
03.08.2023 14:25Поскольку наш собеседник сразу заявил, что общепринятое определение графа ему не указ, и что "граф это неопределяемое понятие, понимаемое на уровне интуиции", то он теперь может назвать "графом" что угодно, хоть синусоиду. И никаких противоречий в его рассуждениях не возникнет. Очень удобно! :)

GospodinKolhoznik
03.08.2023 14:25Не вообще все, что угодно, а все что угодно, интуитивно понимаемое как граф.
Вы же не будете спорить, что невозможно определить точку из геометрии. Значит ли это, что точкой можно назвать синусоиду?

GospodinKolhoznik
03.08.2023 14:25+1Мне кажется я достаточно убедительные доводы предоставил к своим аргументам. Вы их никак не можете опровергнуть зато отмахиваетесь, обвиняя меня в том, что я типичный пример Даннинга - Крюгера. В научном диспуте так поступать не этично. Ещё раз - если вы не хотите или не можете дискутировать, не дискутируйте. А просто прибежал, обвинил человека в том, что он мало чего понимает и убежал никак не удосужившись подтвердить свои слова, это как то недостойно.
В научных спорах не принято бравировать авторитетом и регалиями, а принято приводить логические доводы и агрументы, но мои аргументы вы проигнорировали, сославшись на то, что предмету уже сотни лет, видимо намекали на то, что такой почтенный возраст уже сам по себе авторитет. Ну а арифметике уже 10 тысяч лет, но до сих пор ведутся ожесточенные споры по ее аксиоматике.
Ну если вам логических доводов недостаточно, и необходим авторитет, то у меня есть 2 опубликованные статьи по математике. Не в области теории графов, а в области теории случайных процессов, но тем не менее, я вас уверяю, что основы теории множеств и логики я кое-как, худо-бедно знаю. Не знаю, право, достаточный ли это аргумент, чтобы вы перестали считать меня типичным примером Даннинга - Крюгера, если честно, я думал что и моих логических доводов должно быть достаточно, но как показала практика люди здесь логику не очень то уважают.

tonitaga Автор
03.08.2023 14:25Так там же есть заголовок перед этим, "Представление графа в коде", потому что без этого было бы непонятно такое выражение graph(v1, v2), а до этого есть заголовок, про сам граф, где я отставил ссылки для ознакомления с самим понятием графа.

dgoncharov
03.08.2023 14:25+7По каким критериям вы отобрали эти 5 алгоритмов как "основные"? Ну ладно, обход в ширину и глубину - наверное, и правда. А остальные? Почему, к примеру, не алгоритмы раскраски графа? Или поиска паросочетаний? Или поиска полносвязного подграфа? Или решения "задачи коммивояжера"?
Впрочем, ответ на эти вопросы предположить нетрудно: вы описали те алгоритмы, которые знаете сами. Но не вводите, пожалуйста, людей в заблуждение, заявляя, что "все основные алгоритмы будут находится в одном посте". Алгоритмов на графах хватит на несколько книг. Даже если ограничиться наиболее известными и важными, все равно это потребует книги, а не поста. И такие книги уже написаны. (Думаю, именно это и имеют в виду те, кто пишет "спасибо, не надо".)Ну и наконец, алгоритмы интересны тем, какие задачи они решают, а не тем, в честь кого они названы. Оглавление статьи очень неудачное.

tonitaga Автор
03.08.2023 14:25Например, задача коммивояжера, эта та задача и алгоритм ее решения точно тема отдельной статьи. А BFS DFS это база, да и кратчайшие пути межд вершинами и всеми парами вершин, как по мне база. Согласен, что и целой книги не хватит для описания алгоритмов на графах.

thevlad
03.08.2023 14:25Про статью "решения задачи коммивояжера" вы явно пошутили, там просто про один из наиболее эффективных подходов к точному решению - монография страниц на 500. И без мат подготовки, вы просто не поймете, что там написано.
Про "аппроксимирующие" алгоритмы и методы локальной оптимизации, применительно к этой задаче, еще можно одну книгу написать.

tonitaga Автор
03.08.2023 14:25Алгоритм там не сложный, сложнее его понять и реализовать, как раз для этого придется прочитать не мало тех.материала, согласен, но в одну статью это уместить можно, убрав воду. Причем в таких книгах больше половины (как по мне) просто дискуссия и обсуждения, доказательства, теоремы и т.п.

ElectricPigeon
03.08.2023 14:25С моей точки зрения, доказательство того, почему работает алгоритм — это одна из самых интересных вещей, достойных упоминания в статье (зависит от темы статьи, конечно). Например, почему алгоритм Дейкстры получает корректный результат и чем ему «мешают» рёбра с отрицательным весом.
По содержанию статьи: по-моему, Вы перепутали, какой из алгоритмов найдёт кратчайший путь в лабиринте. Это должен быть BFS. DFS найдёт путь, но не обязательно кратчайший.

tonitaga Автор
03.08.2023 14:25Согласен, но смотря как этот лабиринт был сгенерирован, если алгоритмом Эллера, где единственный путь между двумя точками, то DFS тут тоже подходит. Оба подходят, но BFS лучше, согласен, но еще лучше Волновой Алгоритм для этого подходит, хотя принцип действия почти как у BFS

thevlad
03.08.2023 14:25"Алгоритм там не сложный" это вообще о чем? Это NP задача(задача коммивояжера), там единственный не сложный алгоритм - это полный перебор, все остальное там сложное или очень сложное. (может быть за исключением совсем наивных "жадных" алгоритмов)

lomonoga
03.08.2023 14:25Нет описания алгоритмов простыми словами
Реализация по пунктам это хорошо, но что из себя представляет тот же самый dfs? Зачем он и какова его суть?
Без базового понимания что это такое человек даже не сможет придумать куда его впихнуть
Лучше добавить описание под каждый алгоритм



apachik
да, но зачем?
спасибо, лучше не надо :)
apachik
это был такой намек, что хабр начинает превращаться в пикабушечку. Причем не в ту, которая была пару лет назад