
Волновой алгоритм — это алгоритм поиска пути, который использует волновое распространение для определения кратчайшего пути от начальной вершины до целевой вершины.
Название алгоритму дано не случайно, поведение алгоритма соответствует распространению волны, волна огибает препятствия, постепенно заполняя все пространство
Лабиринты и пещеры
Хранение лабиринтов в файле

Лабиринт — структура, состоящая из запутанных путей к выходу.
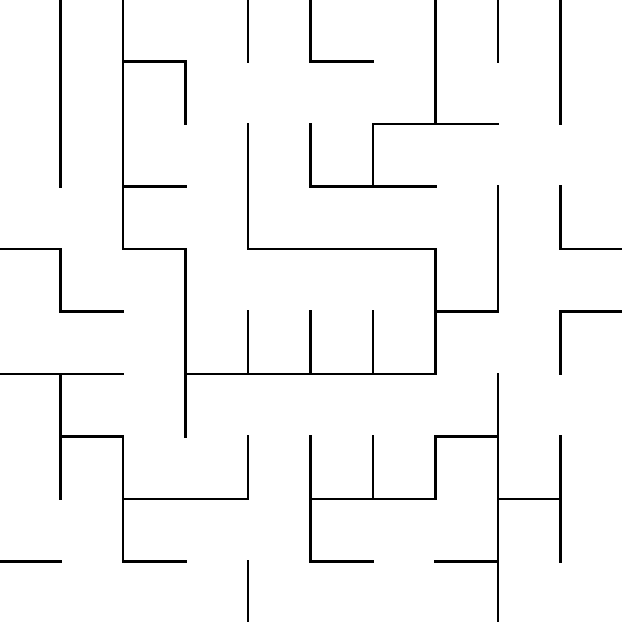
Лабиринт хранится в файле в виде двух матриц — первая матрица говорит о наличии от текущей клетки стены справа, вторая матрица говорит о наличии от текущей клетки стены снизу. (1 - стена есть, 0 - стены нет)
Хранение и использование лабиринта в виде двух матриц позволяет нам выделять меньше памяти, так как если поместить всю информацию в один массив, размер увеличится до 20×20, что составляет 400 клеток, а первый случай хранит всего 200 клеток.
Однако есть и минусы, такой вид хранение увеличивает размер кода, так как мы работает одновременно с двумя массивами.
Хранение пещеры в файле

Пещера хранится в файле в виде матрицы, каждая клетка говорит о том, является ли она стеной или пустотой. (1 - стена, 0 - пустота)
Про генерацию пещер можно прочитать в моей статье по ссылке:
Генерация пещер by tonitaga

Правила волнового алгоритма
Волна будет распространяться по окрестности фон Неймана
Окрестность фон Неймана

Окрестность фон Неймана — совокупность четырёх клеток на квадратном паркете, имеющих общую сторону с данной клеткой.
Конечно, вместо окрестности фон Неймана, можно было использовать окрестность Мура, однако в случае с лабиринтом это невозможно, остановимся на первой окрестности.
Волна, как и в жизни, может распространиться только в ту сторону, где нет препятствия
Последней волной будет считаться та, которая достигла конечной точки, либо которая заполнила все пространство.
Реализация алгоритма на С++
Нахождение кратчайшего пути в пещере
Реализация
В первую очередь нам нужно создать матрицу (массив) длин, где будем хранить расстояния от клетки старта до клетки финиша
CaveWrapper length_map;Что такое CaveWrapper?
CaveWrapper — это структура, которая хранит в себе данные пещеры и позволяет работать с одномерным массивом как с матрицей, структура знает в валидном ли состоянии пещера и знает её размеры
template <>
struct BasicWrapper<kCave> final {
using data_type = std::vector<size_type>;
data_type data;
size_type rows = 0, cols = 0;
bool IsGood() const {
// Some checks
}
size_type &operator()(size_type row, size_type col) {
return data[row * cols + col];
}
size_type operator()(size_type row, size_type col) const {
return data[row * cols + col];
}
};
using CaveWrapper = BasicWrapper<kCave>;Во вторую очередь нам нужно создать массивы распространения волны. Волна будет распространяться постепенно, поэтому нам надо хранить текущее распространение волны и предыдущее распространение, текущая волна будет распространяться в зависимости от предыдущего распространения.
std::vector<Point> wave, old_wave;Также нам нужен будет счетчик для того чтобы знать сколько раз волна распространилась
size_type wave_step = 0;Функция начальной инициализации
Для правильной работы алгоритма, мы в первую очередь должны инициализировать переменные начальными значениями
Матрица длин (length_map) — это самое главное в этом алгоритме, по нему мы и будет находить кратчайший путь. У этой матрицы будет всего два типа значений: -1 (Если волна еще не была в этой клетке) и "неотрицательное число" - расстояние от начальной точки до текущей.
void InitializeStartState(const CaveWrapper &cave, Point from) {
old_wave = {from};
length_map = {CaveWrapper::data_type(cave.rows * cave.cols, -1), cave.rows, cave.cols};
length_map(from.x, from.y) = 0;
}Клетка старта в матрице длин будет помечена как 0, так как расстояние от начальной клетки до начальной и есть 0. От этой клетки и начнется распространение волны.
old_wave будет в себе хранить точку старта, так как последующие волны будут распространяться именно от этой точки.
Распространение волны
Повторюсь, новая волна (wave) будет генерироваться от старой волны (old_wave).
Старая волна хранит в себе лишь последовательность точек на плоскости, от которых и нужно пускать новую волну
Зная массив точек распространения (old_wave), будет пытаться распространять волну дальше, используя окрестность фон Неймана
bool StepWave(const CaveWrapper &cave, Point to) {
++wave_step;
for (auto [row, col] : old_wave) {
for (auto [x, y, value] : {SidePoint{row + 1, col, cave(row + 1, col)},
SidePoint{row - 1, col, cave(row - 1, col)},
SidePoint{row, col + 1, cave(row, col + 1)},
SidePoint{row, col - 1, cave(row, col - 1)}}) {
if (value == 0) {
if (length_map_(x, y) == -1) {
wave.emplace_back(x, y);
length_map(x, y) = wave_step;
}
if (x == to.x and y == to.y)
return true;
}
}
}
old_wave = std::move(wave);
return false;
}Что такое SidePoint?
SidePoint это структура, которая будет хранить в себе координаты соседних клеток и их значение
Зная точки предыдущей волны мы во вложенном цикле определяем соседние точки и их значения, переменная value отвечает за наличие препятствия в данном направлении, и если препятствия нет, то последующим этапом проверяем, была ли волна уже в этой точке, и если волны там еще не было, то мы распространяем новую волну в данном направлении, после каждого распространения мы проверяем не достигли мы конца. Для этого в функцию дополнительным параметром передается точка финиша (Point to)
После того как все возможные распространения были сделаны и волна не достигла конечной точки, мы в старую волну передаем новые точки распространения. (19 строчка).
Восстановление пути
Волновой алгоритм находит все пути сразу, но нам нужен именно кратчайший путь
Для того чтобы получить его, там нужно итеративно вернуться из точки финиша в точку старта, для того чтобы это сделать будем использовать матрицу длин.
Зная значения в матрице длин, будем постепенно возвращаться, чтобы понять куда нам идти (вверх, вниз, вправо, влево), нужно всего лишь сравнить значение текущей клетки и клетки направления, и если клетка направления имеет число меньше чем текущее на 1, то это и есть наш путь.
Путь будем искать пока не дойдем до начальной точки (вспомним, что начальную точку в матрице длин мы инициализировали нулем)
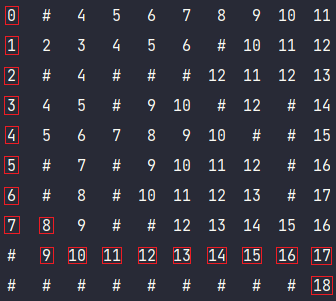
Можно заметить, что это не единственный кратчайший путь, но мы выберем один из многих
std::vector<Point> MakePath(const CaveWrapper &cave, Point from, Point to){
std::vector<Point> path{to};
auto &[row, col] = to;
while (length_map_(row, col) != 0) {
// TOP
if (length_map_(row + 1, col) + 1 == length_map_(row, col) and cave(row + 1, col) == 0)
++row;
// BOTTOM
else if (length_map_(row - 1, col) + 1 == length_map_(row, col) and cave(row - 1, col) == 0)
--row;
// RIGTH
else if (length_map_(row, col + 1) + 1 == length_map_(row, col) and cave(row, col + 1) == 0)
++col;
// LEFT
else if (length_map_(row, col - 1) + 1 == length_map_(row, col) and cave(row, col - 1) == 0)
--col;
else
return {}; // Если некуда идти, значит пути нет
path.emplace_back(to);
}
path.back() = from;
return path;
}Общий вид функции
std::vector<Point> Solve(const CaveWrapper &cave, Point from, Point to) & {
if (!cave.IsGood() or cave(from.x, from.y) == 1 or cave(to.x, to.y) == 1)
return {};
InitializeStartState(cave, from);
while (!old_wave_.empty()) {
if (StepWave(cave, to))
break;
}
return MakePath(cave, from, to);
}Нахождение кратчайшего пути в лабиринте
Реализация
В целом реализация отличается лишь тем, что при обработке пещеры мы работаем с одним массивом, а в случае лабиринта с двумя массивами. В остальном алгоритм ничем не отличается.
В главную функцию будет приходить не пещера а лабиринт тип данных у которого MazeWrapper
Что такое MazeWrapper?
MazeWrapper это структура, которая хранит в себе данные лабиринта и позволяет обращаться в одномерным массивам как к матрицам, все это благодаря перегруженному оператору круглых скобочек
template <>
struct BasicWrapper<kMaze> final {
using data_type = std::vector<size_type>;
data_type right, bottom;
size_type rows = 0, cols = 0;
bool IsGood() const {
// Some checks
}
size_type &operator()(size_type row, size_type col, bool is_right = true) {
return is_right ? right[row * cols + col] : bottom[row * cols + col];
}
size_type operator()(size_type row, size_type col, bool is_right = true) const {
return is_right ? right[row * cols + col] : bottom[row * cols + col];
}
};
using MazeWrapper = BasicWrapper<kMaze>;Из-за того что лабиринт хранит два массива, в операторе круглых скобок добавлен bool параметр, чтобы извне можно было выбирать один из двух массивов.
Отличие будет при определении соседей для распространения новой волны и при нахождении кратчайшего пути (все это связано с тем как эти данные мы храним с структуре)
Распространение волны
bool StepWave(const MazeWrapper &maze, Point to) {
++wave_step;
for (auto [row, col] : old_wave) {
for (auto [x, y, value] : {SidePoint{row + 1, col, maze(row, col, false)},
SidePoint{row - 1, col, maze(row - 1, col, false)},
SidePoint{row, col + 1, maze(row, col)},
SidePoint{row, col - 1, maze(row, col - 1)}}) {
if (value == 0) {
if (length_map(x, y) == -1) {
wave.emplace_back(x, y);
length_map(x, y) = wave_step;
}
if (x == to.x and y == to.y)
return true;
}
}
}
old_wave = std::move(wave);
return false;
}Восстановление пути
В моем случае лабиринт генерируется используя Алгоритм Эллера, это говорит о том, что в лабиринте от любых двух точек существует всего один путь, его мы и будем искать.
Полезная статья по алгоритму Эллера
Алгоритм Эллера

Можно заметить что слева от клетки со значением 20 есть клетка 19, на первый взгляд кажется что можно повернуть в эту сторону, однако там стенка, поэтому перед каждый поворотом нужно проверять нет ли стенки там, куда мы поворачиваем. Если этого не сделать то, путь будет проходить сквозь стены лабиринта, что является неверным решением задачи.
std::vector<Point> MakePath(const MazeWrapper &maze, Point from, Point to){
std::vector<Point> path{to};
auto &[row, col] = to;
while (length_map_(row, col) != 0) {
// LEFT
if (length_map_(row, col - 1) + 1 == length_map_(row, col) and maze(row, col - 1) == 0)
--col;
// RIGHT
else if (length_map_(row, col + 1) + 1 == length_map_(row, col) and maze(row, col) == 0)
++col;
// BOTTOM
else if (length_map_(row - 1, col) + 1 == length_map_(row, col) and maze(row - 1, col, false) == 0)
--row;
// TOP
else if (length_map_(row + 1, col) + 1 == length_map_(row, col) and maze(row, col, false) == 0)
++row;
else
return {}; // Если некуда идти, значит пути нет
path.emplace_back(to);
}
path.back() = from;
return path;
}Общий вид функции
std::vector<Point> Solve(const MazeWrapper &maze, Point from, Point to) & {
if (!maze.IsGood())
return {};
InitializeStartState(maze, from);
while (!old_wave_.empty())
if (StepWave(maze, to))
break;
return MakePath(maze, from, to);
}Полезные ссылки
Хочу поделиться своим github'ом, буду признателен если вы оформите подписку:
GitHubСтатья, написанная мной, по генерации пещер:
Генерация пещерПолезная статья по генерации лабиринта:
Алгоритм ЭллераЕсли возникли вопросы по реализации алгоритма, пишите в телеграм:
@tonitaga
Комментарии (13)

saboteur_kiev
01.07.2023 14:05-4алгоритм совсем без оптимизации. Имхо он вообще не пытается найти кратчайший путь, а просто хоть какой-то, с приоритетом вверх, а потом влево.
Можно было бы поставить хотя бы один анализ на упреждение, шага вперед, получилось бы значительно лучше..

wataru
01.07.2023 14:05+3Нет, алгоритм находит кратчайший путь. Доказывается по индукции по длине пути. Потому что он сначала посетит все клетки на расстоянии 0 (одна начальная), потом все клетки на расстоянии 1, потом все на расстоянии 2 и т.д.

saboteur_kiev
01.07.2023 14:05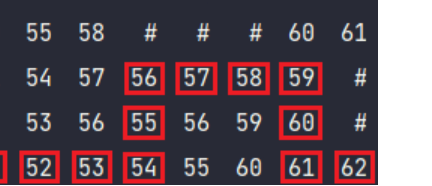
То есть вот тут на картинке, нельзя было сразу напрямую влево пойти, надо было вверх?
Или я не понимаю смысла этой картинки?
tonitaga Автор
01.07.2023 14:05+1Там стена, я это в части про реализацию кода для лабиринта упомянул

Alexandroppolus
01.07.2023 14:05+2Думаю, всё-таки стоило нарисовать эти стены, без них картинка выглядит совсем непонятно..



wataru
А как этот алгоритм связан с алгоритмом обхода в ширину? Чем отличается?
tonitaga Автор
Практически ничем не отличается, так как Волновой алгоритм относится к семейству алгоритмов основанных на методах поиска в ширину.
GospodinKolhoznik
Волновой звучит круче! На ум сразу приходят волновая функция, тфкп, уравнение Шредингера и т.п.
Алгоритм обхода в ширину звучит как то проще и приземлённее. А вот если бы он назывался Алгоритм Сопряженно-Резонирующего Стохастического Осциллятора, то было бы совсем круто! Если когда ни будь придумаю какой ни будь алгоритм, обязательно так его и назову, и неважно, что он из себя будет представлять, под такое заковыристое название можно натянуть любую логику работы.
MiXei4
Для меня всегда было наоборот. Волновой алгоритм - это что-то очень простое на матрице. Запустил волну из клетки, нашёл путь - очень просто для представления и понимания. А обход в ширину - это уже теория графов, другой уровень.
orenty7
Это один в один обход в ширину. Разница лишь в том, что при обходе в ширину клетки, которые нужно обойти, ставятся в одну очередь, а тут они "разделены на эпохи". Те же яйца только в профиль