Моделирование нелинейных функций и ограничений в задачах линейного программирования / forpes.ru

Главная
Моделирование нелинейных функций и ограничений в задачах линейного программирования

Моделирование нелинейных функций и ограничений в задачах линейного программирования +6

09.10.2023 08:51

Lozkins 0 1100 Источник

Особые формулировки ограничений, целевой функции или допустимой области принимаемых значений переменных переводят задачи из простого линейного случая в более сложный - нелинейный. Используя достаточно ограниченный спектр математических преобразований (введение и замена переменных, добавление вспомогательных ограничений), разберем процедуры линеаризации некоторых нелинейных задач.

Материал организовал следующим образом:

Преобразования, которые приводят к задаче линейного программирования (ЛП). Они также могут быть перенесены и на задачи смешанного целочисленного программирования (ЦЛП).
Преобразования, которые приводят к задаче ЦЛП.
Аппроксимация нелинейности с помощью кусочно-линейных функций. В этом случае получим приближение с некоторой ошибкой. Управлять этой ошибкой можно посредством количества и длины интервалов.

Нелинейность преобразуем в ЛП

Введем обозначения, а именно, постановку задачи ЛП в стандартной форме:

$\text{minimize} \quad \sum_{j \in J} c_jx_j$ $\sum_{j \in J} a_{ij}x_j \ge b_i, \quad \forall i \in I$ $x_j \ge 0, \quad \forall j \in J$

где x_j - вещественные решающие переменные, c_j - веса переменных в целевой функции, b_i - правая часть ограничений и коэффициенты ограничений $a_{ij}$ . Выкладки будут продемонстрированы для задачи минимизации, но аналогичные операции можно производить для задачи максимизации.

Функция абсолютного значения

Рассмотрим один из вариантов преобразования функции абсолютного значения в целевой функции в виде задачи линейного программирования:

$\text{minimize} \quad \sum_{j \in J} c_j|x_j|$ $\sum_{j \in J} a_{ij}x_j \ge b_i, \quad \forall i \in I$

Заметим, что на переменные не накладываются ограничения неотрицательности. В противном случае, задача будет линейной. Введем две вспомогательные переменные для каждого |x_j| и ограничение, связывающее с текущими переменными модели:

$x_j = x_j^+ - x_j^-, \quad \forall j \in J$

Отметим, что накладываются ограничения неотрицательности на вспомогательные переменные $x_j^+ \ge 0$ и $x_j^- \ge 0$ . Выражение для замены функции абсолютного значения будет иметь вид:

$|x_j| = x_j^+ + x_j^-, \quad \forall j \in J.$

Соберем в конечный вариант задачу ЛП для случая минимизации целевой функции суммы модулей переменных:

$\text{minimize} \quad \sum_{j \in J} c_j(x_j^+ + x_j^-)$ $\sum_{j \in J} a_{ij}(x_j^+ - x_j^-) \ge b_i, \quad \forall i \in I$ $x_j^+, x_j^- \ge 0.$

Задача минимакса

Задачи планирования расписания или реализацию "равномерности" нагрузки на оборудование можно сформулировать в виде задачи минимакса. Например, при планировании производственного расписания целевой функцией может быть минимизация времени выполнения последнего заказа, где последний заказ определяется на основе максимальной даты завершения выполнения заказа.

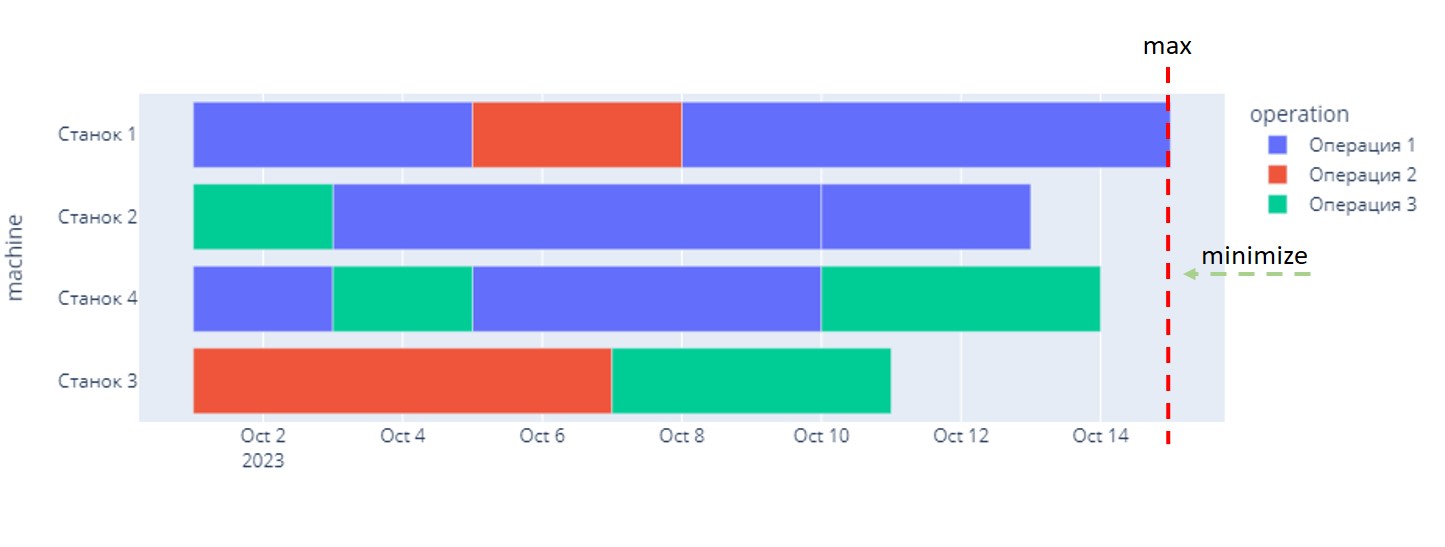
Рассмотрим задачу минимакса следующего вида:

$\text{minimize} \quad \max \{\sum_{j \in J} c_{1j}x_j, \dots, \sum_{j \in J} c_{Kj}x_j\}$ $\sum_{j \in J} a_{ij}x_j \ge b_i, \quad \forall i \in I$ $x_j \ge 0, \quad \forall j \in J$

где целевая функция представляет собой минимизацию максимума линейных выражений. Для формулировки эквивалентной линейной задачи потребуется ввести одну переменную и неравенств:

$z = \max \{\sum_{j \in J} c_{1j}x_j, \dots, \sum_{j \in J} c_{Kj}x_j\}$ $\sum_{j \in J} c_{ij}x_j \le z, \quad \forall i \in [1, \dots, K]$

Итоговая формулировка задачи минимакса в виде задачи ЛП имеет следующий вид:

$\text{minimize} \quad z$ $\sum_{j \in J} a_{ij}x_j \ge b_i, \quad \forall i \in I$ $\sum_{j \in J} c_{ij}x_j \le z, \quad \forall i \in [1, \dots, K]$ $x_j \ge 0, \quad \forall j \in J$

Дробно-линейная функция

Пожалуй, самое интересное преобразование. Целевая функция в дробно-линейном виде возникает при оптимизации таких показателей, как рентабельность, оборачиваемость, маржинальность и др. Задача выглядит следующим образом:

$\text{minimize} \quad \frac{\sum_{j} c_j x_j + c_0}{\sum_{j}d_j x_j + d_0}$ $\sum_{j \in J} a_{ij}x_j \ge b_i, \quad \forall i \in I$ $x_j \ge 0, \quad \forall j \in J,$

где c_0 и d_0 - свободные члены линейных выражений (числителя и знаменателя), а c_j и d_j - веса переменных в числителе и знаменателе дробно-линейной функции соответственно.

Предположение! Зафиксируем, что знаменатель дробно-линейной функции может быть только положительным или только отрицательным на множестве возможных значений переменных.

Начнем с введения |J| + 1 вещественных переменных y_j и , которые связаны с переменными задачи следующим образом y_j = z*x_j . Произведение вспомогательной переменной на решающую переменную модели выглядит как усложнение. Здесь закралась многоходовочка, пройдемся по шагам.

Не нарушая общности, рассмотрим случай, когда

$\sum_{j}d_j x_j + d_0 > 0$ . Для случая $\sum_{j}d_j x_j + d_0 < 0$ справедливы аналогичные преобразования, так же можно вынести знак "-" в дробь.

Шаг 1. Произведем замену знаменателя целевой функции на , т.е.

$z = \frac{1}{\sum_{j}d_j x_j + d_0}.$

С учетом обозначения и предположения о положительности знаменателя задача запишется следующим образом:

$\text{minimize} \quad \sum_{j} c_j x_jz + c_0z$ $\sum_{j \in J} a_{ij}x_j \ge b_i, \quad \forall i \in I$ $\sum_{j}d_j x_jz + d_0z = 1$ $z > 0, x_j \ge 0, \quad \forall j \in J$

Шаг 2. Воспользуемся предположением, что

z > 0 . Умножим исходные ограничения задачи на и заменим все произведения z*x_j на y_j :

$\text{minimize} \quad \sum_{j} c_j y_j + c_0z$ $\sum_{j \in J} a_{ij}y_j \ge b_iz, \quad \forall i \in I$ $\sum_{j}d_j y_j + d_0z = 1$ $z > 0, x_j \ge 0, \quad \forall j \in J$

Шаг 3. Чтобы получить задачу в виде задачи ЛП, необходимо решить вопрос с

z >0 . Здесь возможны два пути: либо взять некоторый малый $\epsilon > 0$ и положить $z \ge \epsilon$ , либо допустить ситуацию, когда z = 0 , т. е. $z \ge 0$ . Таким образом, свели дробно-линейную целевую функцию к задаче ЛП.

Восстановление оптимальных значений переменных x_j можно получить путем деления оптимальных значений переменных y_j на оптимальное значение переменной .

Нелинейные задачи преобразуем в ЦЛП

Целочисленные переменные позволяют расширить список нелинейных функций, которые можно свести к линейным. Однако, обилие вспомогательных переменных может серьезно повлиять на скорость поиска оптимального решения.

Область допустимых значений переменной разбита на несколько интервалов

Случай 1. Пусть множество допустимых значений переменной $x \in \{0\} \cup [a, b]$ , где 0 < a < b . Используя одну бинарную переменную и два линейных ограничения, возможно определить такую область допустимых значений :

$x \ge ay$ $x \le by$

Переменная называется переменной-индикатором, а смысловая нагрузка на нее следующая:

$y = \begin{cases} 0, \quad x = 0 \\ 1, \quad x \in [a, b] \end{cases}$

Случай 2. Пусть множество допустимых значений переменной $x \in[a_1, b_1] \cup [a_2, b_2]$ , где b_1 < a_2 . Используя одну бинарную переменную и два линейных ограничения, возможно определить такую область допустимых значений :

$x \le b_1 + (b_2 - b_1)y$ $x \ge a_2 - (a_2 - a_1)(1 - y)$

Переменная-индикатор реализует следующую зависимость:

$y = \begin{cases} 0, \quad x \in [a_1, b_1] \\ 1, \quad x \in [a_2, b_2] \end{cases}$

В случае, когда имеем непересекающихся интервалов, описывающих допустимые значения переменной $x \in [a_1, b_1] \cup \dots \cup [a_n, b_n]$ , где $b_i < a_{i+1} \forall i \in [1, \dots, n-1]$ , применяем подход из предыдущего сценария:

$x \ge a_iy_i, \quad \forall i \in [1, \dots, n-1]$ $x \le b_iy_i, \quad \forall i \in [1, \dots, n-1]$ $\sum_{i=1}^n y_i = 1.$

Здесь переменная y_i принимает значение 1, если выбран -ый интервал. При этом, будет выбран ровно один интервал, исходя из последнего ограничения.

Случай 3. Пусть имеем полностью дискретное множество для описания допустимых значений переменной $x \in \{a_1, \dots, a_n\}$ . Моделирование такого множества допустимых значений потребует инициализации переменных-индикаторов и два ограничения, каждому элементу множества соответствует одна бинарная переменная.

$x = \sum_{i=1}^n a_iy_i$ $\sum_{i=1}^n y_i = 1.$

Выполнение как минимум одного ограничения (Either-or)

Рассмотрим случай, когда у нас есть два ограничения, из которых достаточно выполнить только одно. Такой способ задания ограничений выходит за пределы ЛП, где необходимо выполнять все сформулированные ограничения. Подобные ограничения возникают при построении расписаний, где возможны несколько веток производства одного и того же продукта/полуфабриката.

$\text{minimize} \quad \sum_{j \in J} c_jx_j$ $\sum_{j \in J} a_{1j}x_j \le b_1 \quad \vee \quad \sum_{j \in J} a_{2j}x_j \le b_2$ $x_j \ge 0, \quad \forall j \in J$

Вспомогательные атрибуты: переменная-индикатор и две константы M_1 и M_2 . Константы необходимо выбрать таким образом, чтобы $\sum_{j \in J} a_{1j}x_j - b_1 < M_1$ и $\sum_{j \in J} a_{2j}x_j - b_2 < M_2$ , при этом достаточно близкими к максимальным возможным значениям этих сумм соответственно. Преобразование ограничений в ЛП имеет следующий вид:

$\text{minimize} \quad \sum_{j \in J} c_jx_j$ $\sum_{j \in J} a_{1j}x_j \le b_1 + M_1y$ $\sum_{j \in J} a_{2j}x_j \le b_2 + M_2(1 - y)$ $x_j \ge 0, \quad \forall j \in J.$

Условные ограничения

Здесь рассмотрим классическую связку условного выражения: если выполняется $\sum_{j \in J} a_{1j}x_j \le b_1$ , то $\sum_{j \in J} a_{2j}x_j \le b_2$ тоже должно выполняться.

Прежде чем перейти к манипуляциям с ограничениями, отступление в сторону булевой алгебры. Обозначим первое ограничение событием , а второе ограничение - событием . Если первое ограничение выполняется (=Истина), то второе ограничение тоже выполняется (=Истина), это условие соответствует оператору импликации ( A → B ). В свою очередь, $A → B = \lnot(A \wedge \lnot B)$ . Используя закон де Моргана, получим $A → B = \lnot A \vee B$ .

Воспользуемся выкладками из булевой алгебры. Под отрицанием логично понимать смену знака (дополнение). В нашем случае развернем знак на строго больше:

$\sum_{j \in J} a_{1j}x_j > b_1$ . В целом получается очень знакомая картина:

$\text{minimize} \quad \sum_{j \in J} c_jx_j$ $\sum_{j \in J} a_{1j}x_j > b_1 \quad \vee \quad \sum_{j \in J} a_{2j}x_j \le b_2$ $x_j \ge 0, \quad \forall j \in J.$

Пренебречь строгим неравенством, как это было в случае дробно-линейной функции, к сожалению, нельзя в силу строгости приведенных мат. преобразований. Но мы можем добавить в правую часть первого ограничения маленькую величину

$\epsilon > 0,$ которая "особо" не влияет на решение (например, границу требуемой точности решения).

$\sum_{j \in J} a_{1j}x_j \ge b_1 + \epsilon$

Последующие шаги нам уже известны: заводим переменную-индикатор , константы и , оценки нижней и верхней границ сумм переменных в соответствующих ограничениях. Собираем все воедино

$\text{minimize} \quad \sum_{j \in J} c_jx_j$ $\sum_{j \in J} a_{1j}x_j \ge b_1 +\epsilon - Ly$ $\sum_{j \in J} a_{2j}x_j \le b_2 + M(1 - y)$ $x_j \ge 0, \quad \forall j \in J.$

Произведение переменных

Сразу обозначу рамки возможностей. Точные преобразования возможны для случаев произведения бинарных переменных и бинарной переменной на целочисленную/вещественную переменную.

Случай 1. Пусть имеем произведение двух бинарных переменных x_1x_2 . Для линеаризации произведения потребуется одна бинарная переменная y = x_1x_2 и три неравенства:

$y \le x_1$ $y \le x_2$ $y \ge x_1 + x_2 - 1.$

Случай 2. Пусть имеем произведение бинарной переменной x_1 на вещественную x_2 (для целочисленной аналогично), кроме того, пусть область допустимых значений вещественной переменной ограничена $0 \le x_2 \le u$ . Введем вспомогательную вещественную (целочисленную) переменную y = x_1x_2 и три ограничения:

$y \le ux_1$ $y \le x_2$ $y \ge x_2 - u(1-x_1).$

Аппроксимация в ЦЛП

Выше рассматривали кейсы полностью эквивалентных преобразований нелинейных функций и ограничений в задачу ЛП/ЦЛП. Здесь рассмотрим приближенный переход от нелинейной функции к ее линейному приближению.

Конечно, если разложение в ряд Тейлора нелинейной функции обеспечивает нужную точность на уровне взятия линейных членов, то дальнейшие выкладки избыточны.

Special Ordered Set (SOSs)

В ЦЛП есть ограничения специального вида SOS1 и SOS2. Знание, что переменные образуют упорядоченное множество, позволяет повысить производительность метода ветвей и границ при решении задачи ЦЛП. Переменные, которые формируют множество типа SOS, могут быть как вещественными, так и целочисленным (бинарными, в частности).

В рамках этого материала не будем погружаться в детали учета специфики SOS в алгоритме ветвей и границ. Но ограничения типа SOS2 нам потребуются в последующем описании схемы аппроксимации нелинейных функций. Ограничимся их определениями:

SOS1 - набор переменных, значения которых могут быть отличными от нуля для не более чем одной переменной из набора. Важным является условие, что нет других дополнительных ограничений на отдельные переменные множества. Т.е. они должны встречаться полным набором в других ограничениях.

SOS2 - упорядоченный набор переменных, в котором не более двух соседних элементов могут быть ненулевыми в допустимом решении. Любые другие ограничения математической модели либо используют весь набор переменных множества SOS2, либо не используют их вообще.

Линейное приближение нелинейных функций

Аппроксимацию нелинейных функций будем осуществлять кусочно-линейной функцией. Для этого потребуется условие сепарабельности исходной функции нескольких переменных, т.е. $f(x_1, \dots, x_n) = f(x_1) + \dots + f(x_n)$ . Такое условие позволяет решать задачу для каждой функции одной переменной в отдельности.

Рассмотрим на примере функции $f(x) = \log_2 x$ . Пусть x_1, x_2, x_3, x_4 некоторые точки, а f(x_1), f(x_2), f(x_3), f(x_4) соответствующие значения функции f(x) в этих точках. На графике ниже взяты точки 1, 2, 4 и 8, а соответствующие значения логарифма будут 0, 1, 2 и 3.

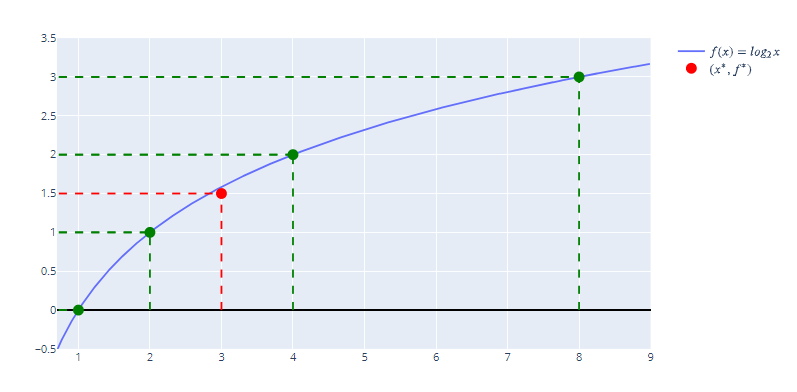
Что подразумевает приближение? Рассмотрим некоторую промежуточную точку между x_2 и x_3 , которую представим в виде взвешенной суммы этих точек

$x^* = \frac{1}{2} x_2 + \frac{1}{2} x_3 = \frac{1}{2} 2 + \frac{1}{2} 4 = 3.$

Тогда исходное приближение логарифма в этой точке будет

$\bar f(x^*) = \frac{1}{2} f(x_2) + \frac{1}{2} f(x_3)= {1}{2} *1 + \frac{1}{2} *2 = 1.5.$

Перенесем эту схему в задачу ЦЛП:

$\bar f(x) = \lambda_1 f(x_1) + \lambda_2 f(x_2) + \lambda_3 f(x_3) + \lambda_4 f(x_4)$ $x = \lambda_1 x_1 + \lambda_2 x_2 + \lambda_3 x_3 + \lambda_4 x_4$ $\lambda_1 + \lambda_2 + \lambda_3 + \lambda_4 = 1$ $\lambda_i \ge 0$

и ограничение типа SOS2 на множестве вещественных переменных $\lambda_i$ обеспечивает выбор одного активного линейного участка дробно-линейной функции для оценки значения исходной функции.

Точность приближения, очевидно, зависит от количества и длины участков дробно-линейной функции. С другой стороны, чем больше участков в модели, тем сложнее задача ЦЛП для поиска решения. При моделировании можно использовать другие свойства функции (перегибы, выпуклость, вогнутость и тому подобное) для упрощения дробно-линейного подобия нелинейной функции.

Заключение

Приведенные выше преобразования нелинейности к задаче линейного программирования возникли, исходя из потребности их прикладного применения. Часть из этих преобразований применял в своих моделях, которые успешно используются на практике. Часть из этих преобразований реализованы в некоторых солверах для моделирования и решения задач ЛП/ЦЛП. Надеюсь, что найдете этот материал полезным и в своих задачах.

Ссылки

Bisschop J. AIMMS optimization modeling, 2006.