На выходных впервые удалось выбраться в Калининград. Я уделил немало внимания исследованию уровня жизни и благополучия области, в основном, ориентируясь на стоимость покупки/аренды жилья, цены в ресторанах и заработок таксистов. Данные достаточно доступные и позволяют сформировать общее представление о положении дел в городе/области.

Помимо экономической составляющей, конечно, старался погрузиться в культурный/исторический аспект жизни города. За короткий промежуток времени достаточно сложно проникнуться всеми особенностями, однако в Калининграде я бы выделил верное следование ограничениям скорости! Благодаря этому, возникает ощущение безопасности, замедления времени и спокойствия.

История города богатая, и в этом мешке событий я нашел кое-что интересное для себя. Речь пойдет о задаче семи пешеходных мостов Кёнигсберга. В свое время Эйлер в процессе размышлений над решением этой задачи положил начало теории графов. В статье рассмотрим задачу с позиции задачи линейного программирования и подтвердим результаты трехсотлетней давности с помощью Python и OR-Tools.

Семь мостов Кёнигсберга

По легенде еще с прусских времен жители Кёнигсберга задавались вопросом: как пройти все пешеходные мосты города так, чтобы маршрут проходил по каждому из мостов ровно один раз. Эйлер в рамках своей деятельности по решению этой задачи комментировал следующее: «Как я слышал, некоторые отрицают, что это можно сделать, другие сомневаются, но никто не подтверждает такой возможности».

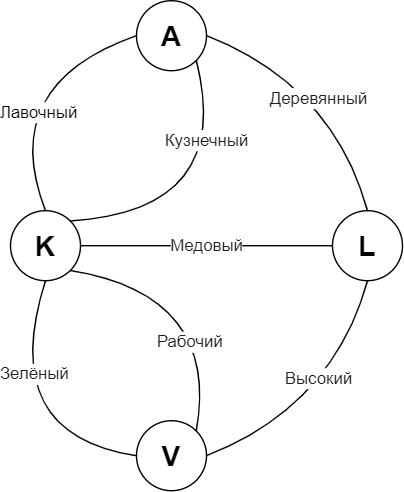
В конце 1542 года было семь мостов и четыре различных берега (Альтштадт, Кнайпхоф, Ломзе и Форштадт). В настоящее время кол-во мостов немного поубавилось, но берега осталиcь прежними. Далее, будем рассматривать исторический период, когда все семь мостов были на месте с теми же условиями задачи какие использовал Эйлер.

В теории графов есть термин Эйлерова цепь - это путь, проходящий по всем рёбрам графа и только по одному разу. Очевидно, прослеживается связь термина и задачи о кёнигсбергских мостах. Собственно, задача состоит в том, чтобы найти Эйлеров путь.

Попробуем развеять таинственность вокруг задачи с помощью современных инструментов для мат. моделирования и решения задач.

Задача удовлетворения ограничений

Воспользуемся теорией графов для моделирования системы мостов Кёнигсберга. Обозначим  - набором вершин в графе, которые соответствуют четырем берегам,  и - множеством направленных ребер графа, которые соответствуют мостам, сам граф обозначим Для моделирования будем предполагать, что граф у нас ориентированный.

Сформулируем потоковую модель с использованием целочисленного линейного программирования (ILP). Для этого введем набор решающих переменных и сформулируем ограничения. Задача состоит в нахождении допустимого решения, поэтому целевая функция отсутствует. Перейдем к обозначениям:

Индексы

- множество узлов сети (соответствуют берегам);

- множество мостов;

- множество направленных переходов по мостам (для каждого моста два направленных ребра);

Переменные

- бинарная переменная, узел начала пути (ограничений на точку старта нет);

- бинарная переменная, узел окончания пути (ограничений на окончание маршрута нет);

- бинарная переменная, проход по мосту в направлении

Ограничения

В задаче указано, что нужно пройти по всем мостам и ровно один раз. В случае потоковой модели добавляются еще несколько ограничений: на связность пути - ребра должны быть последовательными; одна точка начала и одна точка окончания маршрута. Ограничения имеют следующий вид:

• Одна точка начала пути (один исток):

• Одна точка окончания пути (один сток):

• Баланс входов и выходов в узел сети:

• Необходимо пройти по каждому мосту ровно один раз (только в одном направлении):

Вариант постановки задачи не является ее решением. Поэтому перейдем к способу решения сформулированной задачи в виде ILP.

Нахождение Эйлерова пути с OR-Tools

Библиотека OR-Tools позволяет описать задачу ILP и найти ее решение. Для реализации решения будем использовать cp-sat solver, встроенный в OR-Tools. Начнем с установки библиотеки:

pip install ortools

Инициализируем объект модели и входные данные. Каждый мост свяжем с берегом начала и берегом окончания. Для учета направления перехода по мосту введем дополнительный постфикс к названию моста _r - reverse. Таким образом, мы сможем закодировать мосты с использованием только их названия.

from ortools.sat.python import cp_model

model = cp_model.CpModel()

# Участки города, разделенные рекой Преголя
areas = ["Altstadt", "Kneiphof", "Vorstadt", "Lomse"]

# Список мостов
bridges = {
    "lavochniy": ("Altstadt", "Kneiphof"),  # Лавочный мост
    "zeleniy": ("Kneiphof", "Vorstadt"),  # Зелёный мост
    "rabochiy": ("Kneiphof", "Vorstadt"),  # Рабочий мост
    "kuznechniy": ("Altstadt", "Kneiphof"),  # Кузнечный мост
    "derevyanniy": ("Altstadt",  "Lomse"),    # Деревянный мост
    "visokiy": ("Vorstadt", "Lomse"),     # Высокий мост
    "medoviy": ("Kneiphof", "Lomse")      # Медовый мост
}

# Направленные ребра
arcs = {}
for bridge, (_from, _to) in bridges.items():
  arcs[bridge] = (_from, _to)
  arcs[bridge + "_r"] = (_to, _from)

Инициализируем переменные модели. Выше описаны три типа переменных, заведем для них отдельные словари.

# Переменные начала движения
S = {}  # Словарь с переменными start
T = {}  # Славрь переменных terminate

for area in areas:
  var_name = f"s_{area}"  # Название переменной
  S[area] = model.NewBoolVar(name=var_name)

  var_name = f"t_{area}"  # Название переменной
  T[area] = model.NewBoolVar(name=var_name)

# Переменные прохода по мосту
E = {}  # Словарь переменных проходов по мосту (ребра)

for arc in arcs:
  var_name = f"b_{arc}"  # Название переменной
  E[arc] = model.NewBoolVar(name=var_name)

Передадим в модель сформулированные ограничения:

# Ограничение: ровно одна точка начала движения
model.AddExactlyOne(S.values())

# Ограничение: ровно одна точка завершения движения
model.AddExactlyOne(T.values())

# Ограничения: баланс входов и выходов в area
for area in areas:
  # Переменная начала маршрута в area
  start_var = S[area]
  # Переменная окончания маршрута в area
  t_var = T[area]
  # Список входящих потоков в area
  lst_in_vars = [var for key, var in E.items() if arcs[key][1] == area]
  # Список исходящих потоков из area
  lst_out_vars = [var for key, var in E.items() if arcs[key][0] == area]

  # Добавление ограничения в модель
  model.Add(start_var + sum(lst_in_vars) == sum(lst_out_vars) + t_var)

# Ограничение: необходимо пройти по каждому мосту ровно 1 раз
for bridge in bridges:
  model.AddExactlyOne([E[bridge], E[bridge + "_r"]])

Будем использовать встроенный в OR-Tools набор алгоритмов - решатель/solver. Размерность задачи: 13 ограничений и 22 переменных. Задача небольшая, но мало кто захочет решать ее на бумаге. Перейдем к решению:

# Инициализация solver
solver = cp_model.CpSolver()

# # Статистика по модели
# print(model.ModelStats())

# Решение задачи
status = solver.Solve(model)

# Проверяем статус
if status == cp_model.OPTIMAL:
  print('Найден Эйлеров путь!')
elif status == cp_model.INFEASIBLE:
  print('Эйлеров путь не существует!')

Приведу немного теории от Эйлера.

Первая теорема Эйлера, 1736. Граф с двумя или более вершинами имеет эйлеров цикл тогда и только тогда, когда в каждую вершину входит чётное число рёбер.

Вторая теорема Эйлера, 1736. Граф с двумя или более вершинами имеет единственный эйлеров путь тогда и только тогда, когда ровно в две вершины входит нечётное число рёбер.

Следствие. Граф с двумя или более вершинами имеет эйлеров путь тогда и только тогда, когда либо в каждую вершину входит чётное число рёбер, либо ровно в две вершины входит нечётное число рёбер.

В случае мостов Кёнигсберга имеем четыре вершины с нечетным числом ребер, результат модели - Эйлеров путь не существует! Отсутствие решения это тоже решение.

Корректировка постановки задачи

После получения результата напрашивается вопрос, а когда Эйлеров путь будет существовать? Ответ можно получить из следствия теорем Эйлера, или, в нашем случае, скорректировать постановку задачи на: найти максимальное кол-во мостов, когда существует Эйлеров путь.

Воспользуемся прежней моделью, но внесем некоторые изменения. Во-первых, упраздним ограничение на обязательный проход по каждому из мостов. Перезапишем ограничение как: по мосту можно пройти не более чем один раз

Хотим найти максимальное кол-во мостов, которые позволят сформировать Эйлеров путь. Критерий оптимизации зададим в виде следующей целевой функции:

Программная реализация изменений/дополнений модели:

# Ограничение: можно пройти по мосту не более одного раза
# ВНИМАНИЕ! заменяем ограничение: необходимо пройти по каждому мосту ровно 1 раз на следующее
for bridge in bridges:
  model.AddAtMostOne([E[bridge], E[bridge + "_r"]])

# Целевая функция максимаизации кол-ва мостов в пути
model.Maximize(sum(E.values()))

Новая модель допускает путь, в котором не будет ни одного ребра. Если прогулку на месте считать Эйлеровым путем, то решение новой задачи всегда будет существовать - `Найден Эйлеров путь!`.

Посмотрим, какой мост/мосты являются камнем преткновения ... Уже исходя из теоремы Эйлера, видно, что любой мост (один), добавленный или убавленный, сделает задачу решаемой. В рамках моего запуска получилось следующее решение:

Мосты: medoviy_r -> kuznechniy_r -> derevyanniy -> visokiy_r -> rabochiy_r -> zeleniy
Берега: Lomse -> Kneiphof -> Altstadt -> Lomse -> Vorstadt -> Kneiphof -> Vorstadt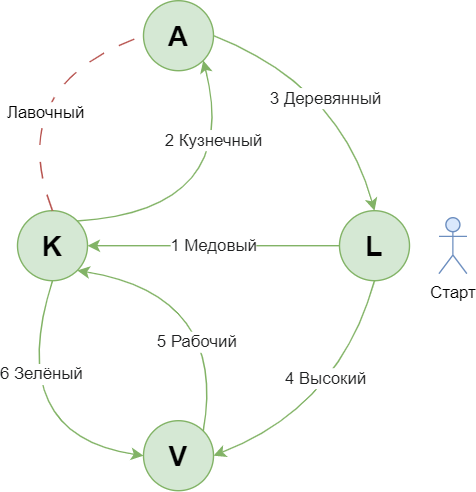

Решение задачи с помощью целочисленного программирования будет неустойчивым, т.е. в зависимости от запуска может быть выдан новый путь. Устранить эту проблему можно за счет добавления разных весов в целевую функцию за прохождение того или иного моста. Вес можно обосновать, например, близостью ресторанов, пунктов по продаже еды или живописностью мостов.

Отмечу, что сохранившиеся пять мостов в Калининграде сегодня позволяют сформировать Эйлеров путь. Кроме того, построенные новые 3 моста также позволяют сформировать такой путь. Поэтому, если будете прогуливаться по Калининграду, можете взять на заметку и прогуляться по Эйлерову маршруту в сегодняшней версии Кёнигсберга.

Ссылки

• Историческая справка и теоремы взяты из википедии;

• Версия статьи в Jupyter notebook.

Схожий материал:

• Модель назначения машин такси на заявки;

• Модель планирования расписаний сотрудников;

• Вводная статья по генерации столбцов.