Проблема множественного тестирования на практике / forpes.ru

09.11.2023 14:40

aspnmrv 0 1100 Источник

Нередко случаются ситуации, когда в A/B экспериментах ~~ну очень хочется~~ нужно проверять сразу несколько гипотез на одном и том же наборе данных, то есть в качестве тестового варианта использовать не одну группу, а сразу несколько. Особенно часто такая необходимость встречается в некоторых областях биологии. Но и в продуктовых командах возникают кейсы, когда, например, уже есть несколько вариантов дизайна каких-то элементов / моделей рекомендаций / ранжирования / etc, и хочется выбрать лучший в рамках одного эксперимента.

Меня зовут Артем Пономарев, я ~~участник клуба анонимных дата-аналитиков~~ Data Analyst, и мне приходилось сталкиваться с множественными экспериментами в продукте. Когда это случалось, и я начинал искать больше дополнительной информации на эту тему, мне показалось, что существует достаточно мало материала с упором на реальную практику в индустрии. Эта статья – попытка структурировать знания о проблеме множественного тестирования, сравнить методы решения проблемы и поделиться практическим опытом работы с множественными экспериментами.

Чо за проблема-то?

При желании можно немного углубиться в историю и увидеть демонстрацию проблемы на полюбившемся мне примере. Итак, лосось.

Кратко: на одной конференции в 2009 году в Сан-Франциско, была представлена научная работа психологов, в рамках которой группа ученых обнаружила способность мозга мертвого лосося воспринимать изображения, которые этому самому лососю показывали. А для особенно заинтересованных всю историю можно почитать, например, тут.

Разумеется, в исследование ученых закралась одна маленькая статистическая деталь, которая и привела к ошибочным результатам, и о которой мы в этой статье и поговорим.

Методы борьбы с ошибкой

Jupyter notebook с примерами и кодом можно найти тут: Github.

Начнем немного издалека, с небольшого примера.

Имеем выдуманный стандартный эксперимент с контрольной и тестовой группами. При этом хотим контролировать вероятность ошибки I рода на заданном уровне 0.05. Сгенерируем данные из нормального распределения с заданными параметрами и убедимся на A/A-тесте, что выбранная статистика (t-test) контролирует ошибку I рода на заданном уровне.

pvalues_list = list()
alpha = 0.05
mu = 5
std = 1
group_size = 200
np.random.seed(42)

for _ in tqdm(range(1000)):
    p_values = list()
    control = np.random.normal(mu, std, group_size)
    treatment = np.random.normal(mu, std, group_size)
    
    pvalue = stats.ttest_ind(control, treatment)[1] # здесь вероятность ошибки I рода = 0.05
    
    if pvalue < 0.05:
        pvalues_list.append(1)
    else:
        pvalues_list.append(0)

print(f"Ошибка I рода: {np.mean(pvalues_list)}")

Ошибка I рода: 0.045

В результате чего получаем вероятность ошибки I рода ~0.05 – как и ожидалось.

Добавим в наш эксперимент еще одну тестовую группу. Теперь эксперимент включает в себя одну контрольную и две тестовые группы, и нам хочется выбрать лучший вариант; а значит придется делать три сравнения: control vs treatment 1, control vs treatment 2, treatment 1 vs treatment 2. Также будем проверять на A/A-тесте, контролируем ли мы ошибку I рода на заданном уровне значимости:

pvalues_list = list()
alpha = 0.05
mu = 5
std = 1
group_size = 200
np.random.seed(42)

for _ in tqdm(range(1000)):
    p_values = list()
    control = np.random.normal(mu, std, group_size)
    treatment1 = np.random.normal(mu, std, group_size)
    treatment2 = np.random.normal(mu, std, group_size)
    
    pvalue_a = stats.ttest_ind(control, treatment1)[1] # здесь вероятность ошибки I рода = 0.05
    pvalue_b = stats.ttest_ind(control, treatment2)[1] # здесь 0.05
    pvalue_c = stats.ttest_ind(treatment1, treatment2)[1] # и здесь 0.05
    
    # итого, вероятность ошибиться хотя бы в одном из случаев = 1 - P(не ошибемся ни разу) = 1 - (0.95 ** 3) ~= 0.14
    
    if pvalue_a < 0.05 or pvalue_b < 0.05 or pvalue_c < 0.05:
        pvalues_list.append(1)
    else:
        pvalues_list.append(0)
  
print(f"Групповая вероятность ошибки I рода: {np.mean(pvalues_list)}")

Получаем вероятность хотя бы раз допустить ошибку I рода при множественном сравнении ~ 0.14, что сильно больше ожидаемого значения. Почему так происходит?
Очевидно, потому что мы добавили два дополнительных перекрестных сравнения, благодаря чему вероятность допустить ошибку хотя бы один раз возрастает.

Визуализация сравнений

Таким нехитрым способом мы попробовали обобщить ошибку I рода на случай наличия множества сравнений. И, в общем-то, это и является первым вопросом и первым этапом при работе с множественным тестированием: каким способом обобщить ошибки при наличии множества сравнений?

FWER

Первый вариант контроля ошибок первого рода – FWER (Family-wise error rate) - групповая вероятность ошибки I рода. Это ровно то, что мы сделали в примере выше.

Так как мы делаем несколько сравнений внутри эксперимента и можем допустить ошибку I рода несколько раз, можем обобщить вероятность ошибок I рода как вероятность допустить хотя бы одну ошибку I рода (m – число гипотез):

$FWER = P(FP > 0) = 1 - (1 - \alpha)^m$

Код для отрисовки графика

import numpy as np
import matplotlib.pyplot as plt

n_list = np.arange(1, 100)

result = {}

for n in n_list:
    result[n] = 1 - (1 - 0.05) ** n

plt.plot(list(result.keys()), list(result.values()))
plt.title("FWER")
plt.xlabel("Number of hypotheses")
plt.ylabel("FWER")
plt.grid()
plt.show()

Скорость роста FWER в зависимости от числа гипотез

FWER быстро растет при росте числа гипотез: при m = 2 FWER ~= 0.1, при m ~= 0.23

Контроль FWER на заданном уровне $\alpha$ :

$FW ER = P(FP > 0) <= \alpha$

На этом этапе мы разобрались с одним из существующих способов обобщить ошибку I рода для случае множества гипотез. А сейчас резко зайдем в самый интересный поворот: поговорим о том, какие существуют методы контроля FWER.

Метод Бонферрони

Самый простой и интуитивно понятный метод для контроля FWER.

Пусть имеем эксперимент с 10 гипотезами и хотим контролировать FWER на уровне значимости 0.05. Мы помним, что при множественном сравнении ошибка I рода будет быстро накапливаться, причем чем больше гипотез – тем быстрее. Так почему бы нам не занизить изначально наши уровни значимости пропорционально числу гипотез? Так мы гарантируем, что будем контролировать ошибку I рода на заданном уровне.

Итак, мы хотим контролировать FWER на уровнях значимости $\alpha_1..\alpha_m$ . Наша задача выбрать $\alpha_1..\alpha_m$ так, чтобы $FWER \le\alpha$ . Тогда определим наши уровни значимости $\alpha_1..\alpha_m$ как $\alpha_i / m$ .

Проверим, контролирует ли метод Бонферрони FWER по сравнению со случаем, когда никаких поправок мы делать не будем, при растущем числе экспериментов.

Контроль FWER методом Бонферрони в зависимости от числа гипотез

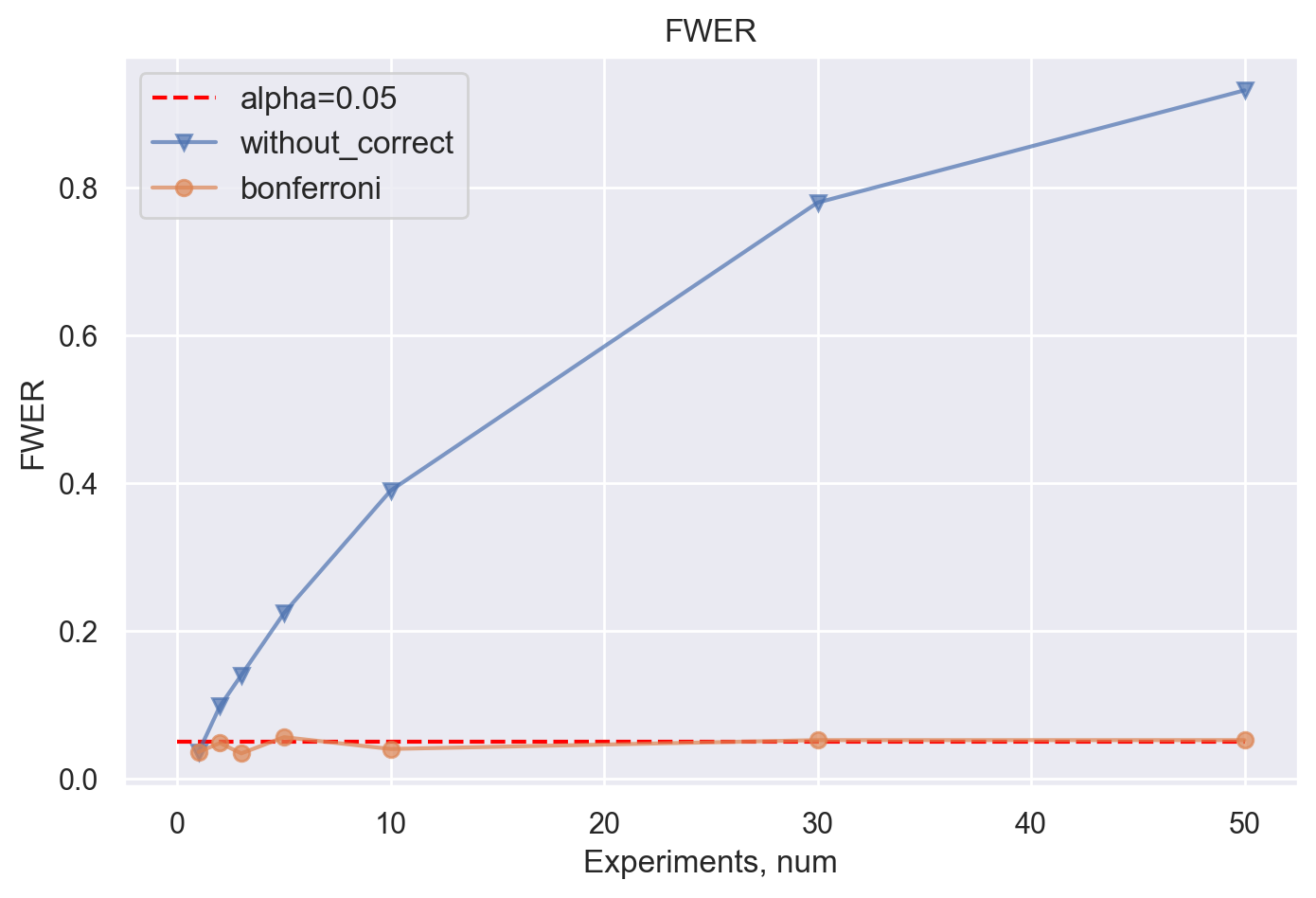
Можем наблюдать, как метод Бонферрони отлично контролирует FWER. Тогда как метод без корректировки уже на десяти сравнениях "накопил" $FWER \sim 0.4$

Проблема метода Бонферрони в том, что таким образом мы сильно перестраховываемся в отношении ошибки I рода, тем самым пропуская истинные эффекты, то есть уменьшаем мощность эксперимента с ростом числа гипотез.

Можем смоделировать эксперимент с разным количеством гипотез и посчитать аналог FWER для ошибки II рода – групповую вероятность ошибки II рода или вероятность допустить хотя бы одну ошибку II рода. Чтобы посчитать такую вероятность, будем добавлять эффект к treatment группе и считать долю случаев, когда мы не нашли эффект, хотя на самом деле он есть.

Контроль групповой вероятности ошибки II рода методом Бонферрони в зависимости от числа гипотез

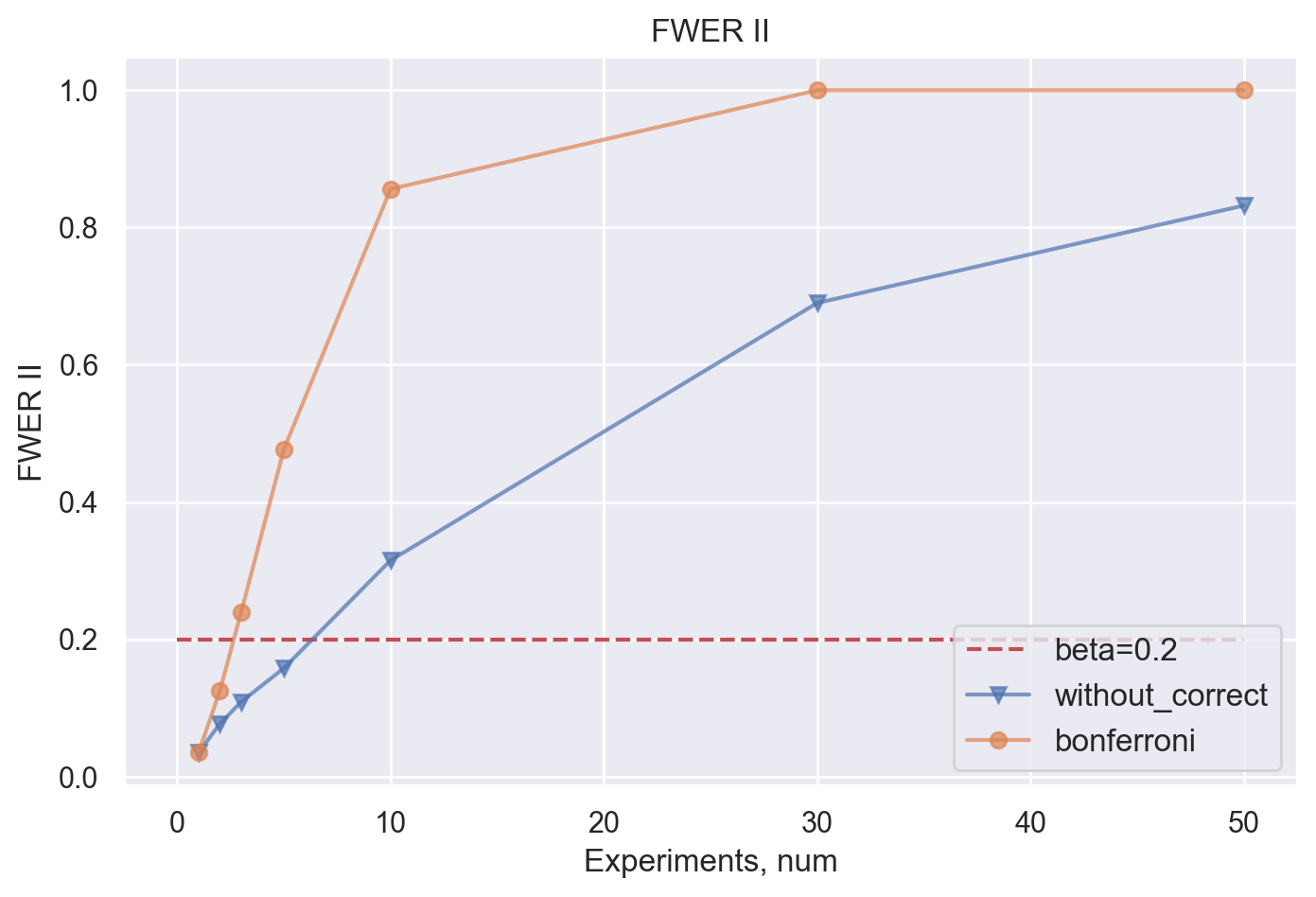
Обобщая, хорошо заметна тенденция быстрого роста групповой вероятности ошибки II рода при использовании метода Бонферрони по сравнению с методом без поправок.

Метод Холма

Метод Холма частично решает проблему метода Бонферрони и позволяет корректировать значения p-value с большей мощностью.

Снова мем для привлечения еще большего внимания

В процедуре Холма, в отличие от метода Бонферрони, сперва считаем p-value, а затем корректируем их в соответствии с процедурой:

Упорядочим значения p-value по возрастанию
Упорядочим соответствующие гипотезы
Далее определим уровни значимости как $\alpha_i = \alpha / (m - i + 1)$

Процедура Холма равномерно мощнее метода Бофнеррони.

Вновь посмотрим на модельные данные для демонстрации уровня контроля FWER методом Холма, сравнивая в том числе с методом Бонферрони.

Контроль FWER методами Бонферрони / Холма

Метод Холма, как и метод Бонферрони контролируют FWER на заданном уровне, в отличие от метода без использования поправок.

Вновь посмотрим на групповую вероятность ошибки II рода, добавив на график метод Холма.

Контроль групповой вероятности ошибки II рода методами Бонферрони / Холма

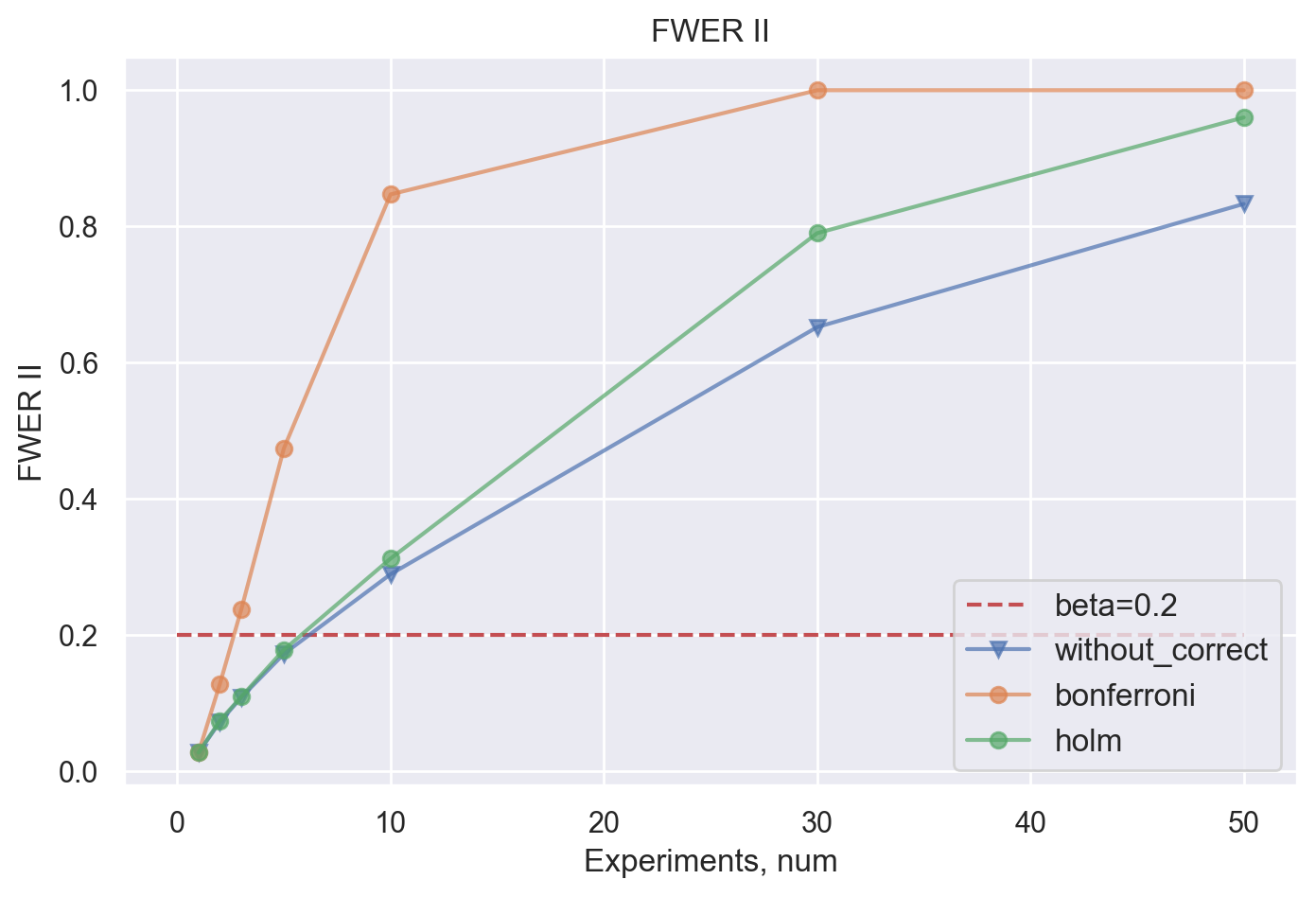
Видим, что метод Холма заметно "мощнее" метода Бонферрони: значение групповой вероятности ошибки II рода при использовании метода Холма при любом числе экспериментов не выше, чем при использовании поправки Бонферрони.

И другие методы, контролирующие FWER..

Существует еще множество методов для контроля групповой вероятности ошибки I рода, но другие известные методы требуют дополнительные предположения о данных для их применения (например, метод Шидака-Холма, требующий предположения о независимости).

Все методы, о которых мы говорили выше, контролируют FWER. Но также все они уменьшают мощность с ростом числа экспериментов: какой-то метод снижает мощность сильно (Бонферрони), какие-то методы равномерно более мощные, но все еще приходится расплачиваться мощностью (Холм, Шидак-Холм).

При этом без дополнительных предположений нельзя построить процедуру более мощную, чем метод Холма. А при условии независимости статистик, нельзя построить процедуру более мощную, чем метод Шидака-Холма.

Да, чтобы как-то исправить ситуацию со снижением мощности, придется от чего-то отказаться (как в жизни обычно и бывает).

Контроль FWER в некоторых ситуациях может быть неоправданно жестким, так как мы пытаемся контролировать совершить хотя бы одну ошибку I рода. Но мы также можем пытаться контролировать, например, долю ложноположительных результатов.

FDR

Еще один вариант контроля ошибок – FDR (False discovery rate).

FDR – это ожидаемая доля ложных отклонений от всех отклонений нулевых гипотез.

$FDR = \mathbb{E} (\frac{FP}{max(FP+TP, 1)})$

На интуитивном уровне отличие FDR от FWER в том, что FDR более "мягко" контролирует ошибку I рода, но также учитывает (в знаменателе) и ошибку II рода. За счет этого методы, контролирующие FDR, более мощные, но в то же время не так жестко контролируют ошибку I рода.

Метод Бенджамини-Хохберга

Один из методов для контроля ожидаемой доли ложных отклонений (FDR). Этот метод обеспечивает контроль FDR на заданном уровне $\alpha$ (при условии независимости статистик).

Вновь смоделируем данные для проверки работы метода, а также для сравнения с другими методами, которые мы рассмотрели ранее.

Для моделирования FDR мы будем добавлять эффект к части экспериментальных групп. Смоделируем три крайних ситуации, чтобы увидеть наиболее полную картину поведения методов при контроле FDR:

половина гипотез с эффектом, половина – без эффекта
одна гипотеза из всех с эффектом, остальные – без эффекта
одна гипотеза из всех без эффекта, остальные – с эффектом

1) Половина гипотез с эффектом, половина – без эффекта

Контроль FDR в зависимости от числа гипотез в случае, когда половина гипотез с эффектом

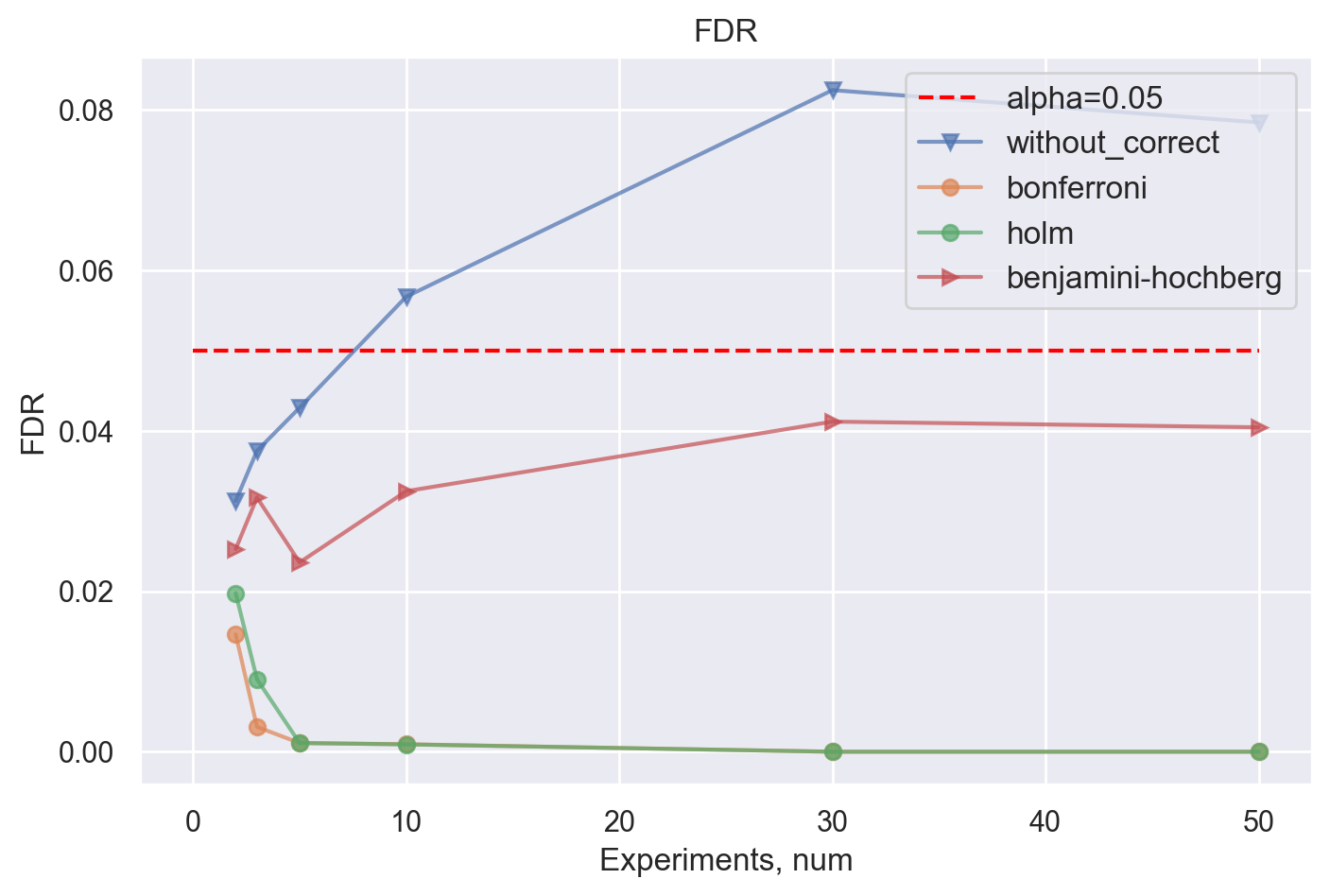
Отметим, что хуже всего справляется метод без каких-либо поправок, что неудивительно. Как неудивительно и то, что методы Холма и Бонферрони контролируют FDR на низком уровне за счет своей более консервативной природы. Метод Бенджамини-Хохберга контролирует FDR на заданном уровне.

2) Одна гипотеза из всех с эффектом, остальные – без эффекта

Контроль FDR в зависимости от числа гипотез в случае, когда одна гипотеза с эффектом

В случае, когда один из N экспериментов с эффектом – метод Бенджамини-Хохберга контролирует FDR на заданном уровне, методы Холма и Бонферрони контролируют FDR на низком уровне. А вот метод без поправок перестает контролировать FDR уже на 5 гипотезах.

3) Одна гипотеза из всех без эффекта, остальные – с эффектом

Контроль FDR в зависимости от числа гипотез в случае, когда одна гипотеза без эффекта

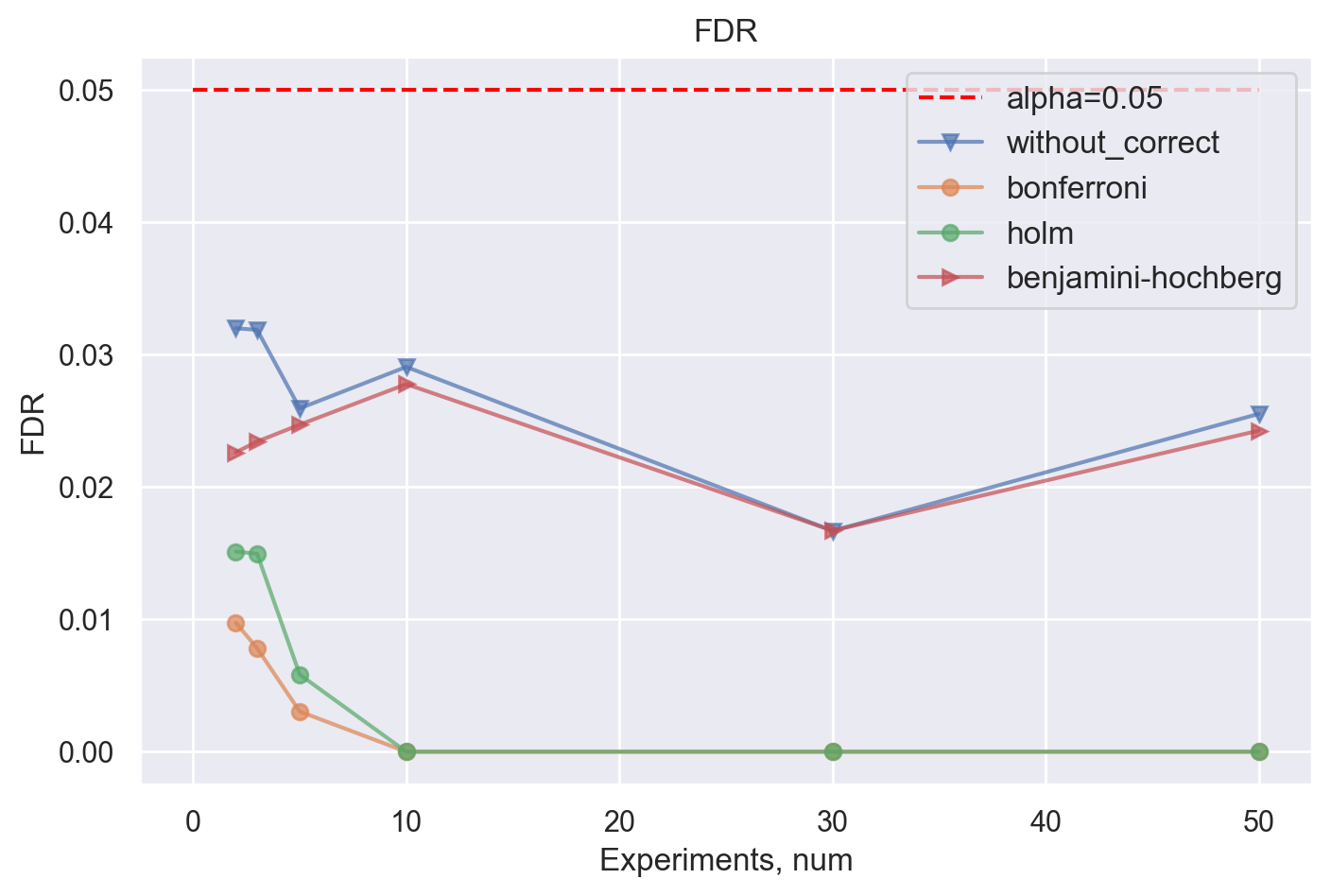
Наконец, в случае, когда только один из N экспериментов без эффекта, метод Бенджамини-Хохберга все также контролирует FDR на заданном уровне.

Метод Бенджамини-Иекутиели

Еще один полезный метод для контроля FDR в копилку, который, в отличие от метода Бенджамини-Хохберга, не накладывает дополнительных ограничений на статистики гипотез.

Что в итоге использовать-то?

Для начала разберемся с метрикой: как выбрать между FWER, FDR или еще чем-то?

Как часто бывает, правильного ответа тут нет. Все зависит от конкретного кейса.

Если имеется множество гипотез, из которых хочется выбрать наиболее "интересные" для дальнейшего анализа, можно опираться на FDR: так мы будем пропускать меньше реальных эффектов, а строгость в отношении ошибки I рода не так важна
Если гипотез немного и тестируется фича, которая потенциально сильно может сказаться на ключевых метриках (например, на деньгах) как отрицательно (в особенности), так и положительно – надежней использовать FWER в силу его бОльшей консервативности в отношении ошибки I рода

Про использование же методов в каждом конкретном случае можно сделать более строгие выводы, тем более что каждый из них мы подробно разобрали на симуляциях.

При использовании FWER оптимально использовать метод Холма (или метод Шидака-Холма в случае независимости статистик) в силу его надежности и в то же время большей мощности по сравнению с другими методами, контролирующими FWER. Но, как мне кажется, полезно сделать оговорку, что если нужно быстро оценить какой-то эксперимент и хочется что-то попроще, то при условии, что сравниваемых гипотез совсем немного (скажем, до 5), вполне нормально использовать метод Бонферрони. Так как при небольшом числе сравнений мы не потеряем сильно в мощности.
Если же мы решили опираться на FDR, то можно использовать как метод Бенджамини-Хохберга, так и метод Бенджамини-Иекутиели

Как учесть при дизайне эксперимента

Напоследок поговорим о том, как учесть проблему множественного тестирования и контроль ошибок на этапе дизайна эксперимента.

Обычно при планировании эксперимента мы должны убедиться, что выбранный критерий для оценки подходит, то есть соответствует ожидаемым значениям ошибок I и II рода (желательно также выбрать наиболее мощный критерий для наших данных, но это уже другая история).

Для этого, как правило, мы используем исторические данные наших целевых метрик: итеративно случайно делим пользователей на control и treatment группы с учетом заранее рассчитанного sample size, рассчитываем значения p-value выбранным критерием и считаем ошибку I рода (или добавляем эффект к treatment-группе и считаем ошибку II рода).

В нашем случае мы заранее знаем, сколько тестовых групп у нас будет и, следовательно, сколько гипотез мы будем проверять. Поэтому далее проделаем следующий шаги:

Для начала необходимо выбрать метрику, которую хотим контролировать: FWER / FDR / etc.
По аналогии с обычным экспериментом возьмем данные по интересующей нас метрике за предыдущий период: в нашем примере мы такую метрику смоделируем.
Затем оценим, какой размер выборки необходим для детекции заданного эффекта
Разделим пользователей на группы и оценим контроль выбранной метрики
При необходимости скорректируем sample size с учетом желаемой мощности

А теперь на примере:

Пусть мы имеем некоторую метрику с нормальным распределением с параметрами $\mu = 10, std = 1, N=100000$ . Ожидаемый минимальный эффект, который хотим детектировать – 0.5%. В примере эксперимента у нас будет 5 групп (1 контрольная и 4 тестовых), мы хотим делать сравнения "все против всех", то есть сравнивать каждую группу с каждой.

Код для генерации симуляции

mu = 10
std = 1
size_group = 1000000

df = pd.DataFrame({"metric": np.random.normal(mu, std, size_group)})

Рассчитаем минимальный объем выборки, необходимый для детекции заданного эффекта с учетом распределения метрики. В данном случае мы будем использовать t-test, поэтому можно было бы рассчитать sample size по формуле, но мы воспользуемся библиотекой Ambrosia.

Код для расчета sample size

from ambrosia.designer import Designer, design, load_from_config

designer = Designer(dataframe=df, metrics="metric")

effects = [1.005, 1.05]  # MDE in percents
first_type_errors = [0.01, 0.05]
second_type_errors = [0.1, 0.2]

designer.set_first_errors(first_type_errors)
designer.set_second_errors(second_type_errors)

designer.run(to_design="size", method="theory", effects=effects)

Получаем, что для детекции эффекта в 0.5% на одну группу необходимо ~6.3K объектов.

Проверим, насколько хорошо в нашем эксперименте контролируется FWER, а также оценим контроль средней ошибки II рода и аналога FWER для ошибки II рода.

Контроль FWER разными методами для симуляции эксперимента

Видим, что поправки хорошо контролируют FWER (за исключением метода Бенджамини-Хохберга, так как он гарантирует только контроль FDR).

Посмотрим, как контролируется средняя ошибка II рода. Для этого будем добавлять эффект ко всем группам, за исключением контрольной: в нашем примере добавляем эффект к 2-5 группам, а первая группа остается в качестве контрольной.

Контроль средней ошибки II рода разными методами для симуляции эксперимента

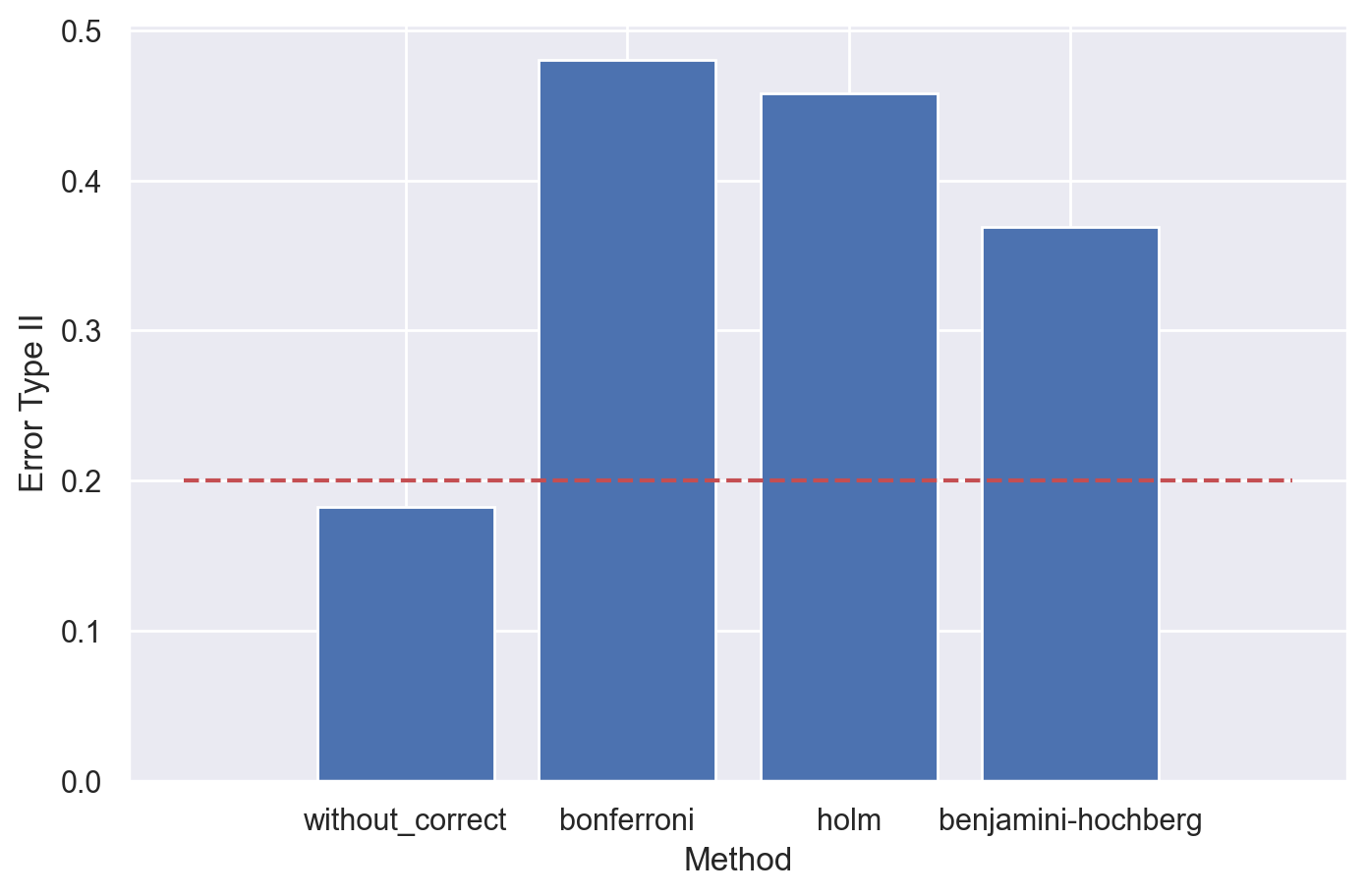
Поправки ожидаемо снижают мощность эксперимента, в особенности методы Бонферрони и Холма, контролирующие FWER. Средняя ошибка II рода при всех сравнениях для методов с поправками выше ожидаемой 0.2.
Но при возможности нам ничего не мешает скорректировать ошибку II рода до ожидаемых значений для выбранного метода поправок.

Мы знаем, что можем уменьшить ошибку путем увеличения размера выборки. Это следует из формулы для расчета размера выборки для случая t-test:

$N > \frac{(Z_\frac{\alpha}{2} + Z_\beta)^2(2*\sigma^2)}{e^2}$

Посмотрим на формулу для расчета минимального размера выборки и вспомним, что наши поправки корректируют значения p-value. Значит, мы можем скорректировать уровни значимости при расчете sample size.

Существуют следующие подходы для коррекции sample size при использовании поправок на множественное тестирование:

Расчет минимального размера выборки на основе наименее благоприятных условий: мы можем рассчитать размер выборки с учетом заданной вероятности ошибок II рода так, чтобы тест с наиболее строгим уровнем значимости $\alpha$ будет иметь необходимую мощность. То есть фактически самый скорректированный уровень значимости генерируется поправкой Бонферрони: в этом случае нужно разделить значение $\alpha$ на число сравнений , то есть $\alpha_i = \alpha_i / m$ . Это будет гарантировать заданную мощность теста;
Другой подход заключается в том, чтобы средняя (или медианная) мощность тестов поддерживалась на заданном уровне. Для случая медианной мощности достаточно $\alpha$ разделить на m / 2. Для поддержания средней мощности на заданном уровне необходимо итеративно посчитать sample size с фиксированными заданными параметрами, разделив заданный уровень значимости $\alpha$ на упорядоченный по возрастанию список числа гипотез и усреднить значение sample size (N – функция для расчета sample size с фиксированными параметрами, за исключением $\alpha$ :

$N = \frac{\sum(N[\alpha / i])}{m}, i=1..m$

Используем на практике оба подхода для демонстрации коррекции sample size.

Код для коррекции sample size с наиболее строгим уровнем значимости

def get_sample_size(mu, std, eff=1.01, alpha=0.05, beta=0.2):
    """"""
    t_a = abs(stats.norm.ppf(alpha / 2, loc=0, scale=1))
    t_b = stats.norm.ppf(1 - beta, loc=0, scale=1)
    

    mu_sqr = (mu - mu * eff) ** 2
        
    z_sqr = (t_a + t_b) ** 2
    disp = 2 * (std ** 2)

    sample_size = int(
        np.ceil(
            z_sqr * disp / mu_sqr
        )
    )
    return sample_size


alpha = 0.05
beta = 0.2

mu = 10
std = 1
effect = 1.005

groups = 5
comparisons = 10

correct_alpha = alpha / comparisons
sample_size_corrected = get_sample_size(mu, std, effect, correct_alpha, beta)

print(f"Скорректированный объем выборки: {sample_size_corrected}")

Скорректированный объем выборки: 10651

В нашем случае в симуляции 5 групп, и мы делаем сравнения "все против всех", то есть всего будем делать 10 сравнений. Значит, для коррекции на основе наименее благоприятных условий, alpha необходимо разделить на 10 и подставить скорректированное значение alpha в формулу для расчета sample size. Получаем скорректированное значение sample size ~10.7K объектов на группу. Размер выборки увеличился на ~70%. Посмотрим на контроль средней ошибки II рода после коррекции размера выборки:

Контроль средней ошибки II рода разными методами после коррекции sample size с учетом наиболее строгого уровня значимости

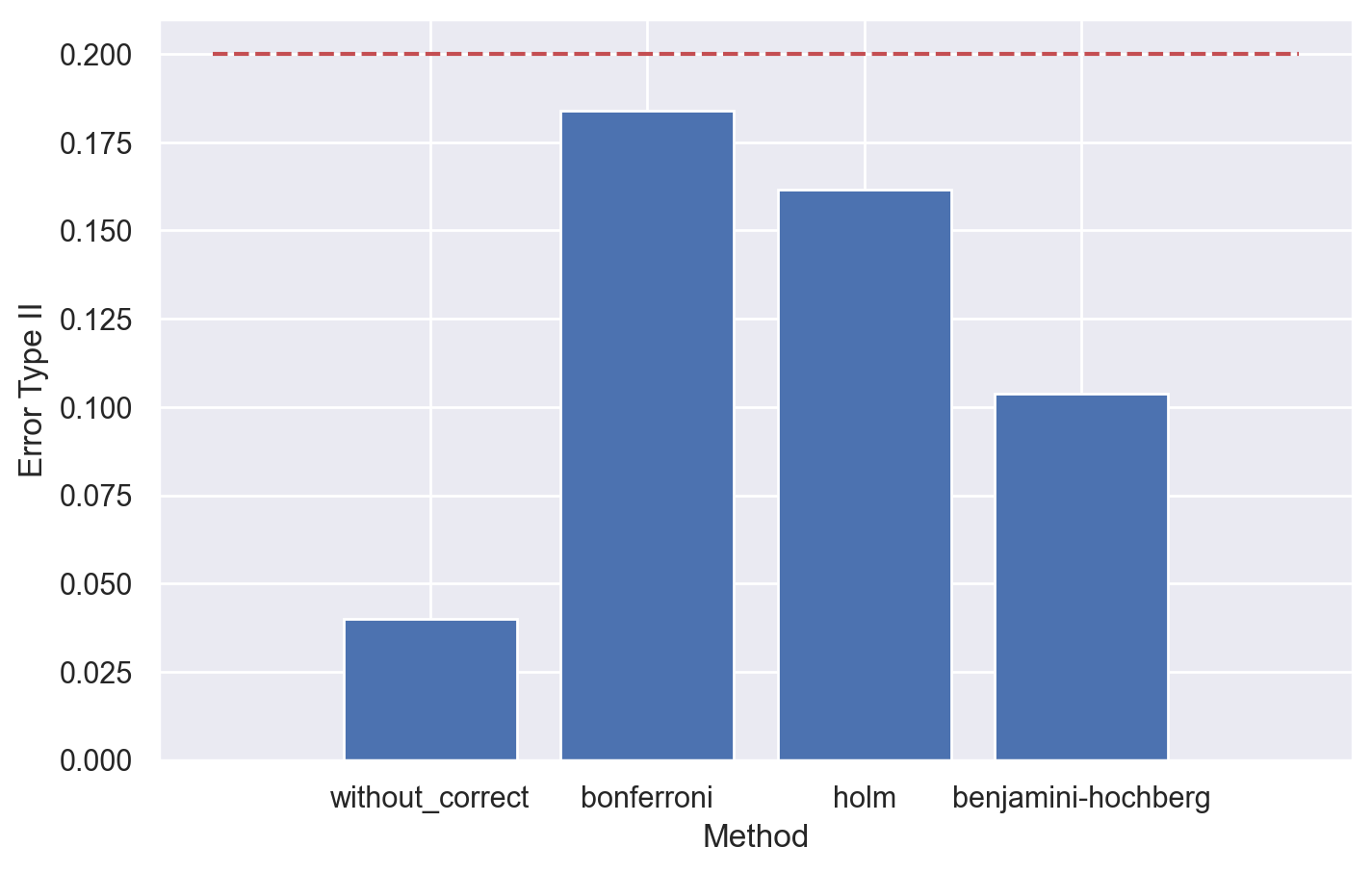
Для метода Холма такая консервативная поправка получилась слишком жесткой: ожидаемо, так как мы корректировали $\alpha$ с наиболее строгим уровнем значимости, в то время как метод Холма равномерно более мощный. Попробуем ориентироваться на расчет sample size с учетом поддержания средней заданной мощности. Для этого будем итеративно делить $\alpha$ на номер сравнения:

Код для коррекции sample size путем поддержания средней заданной мощности

def get_sample_size(mu, std, eff=1.01, alpha=0.05, beta=0.2):
    """"""
    t_a = abs(stats.norm.ppf(alpha / 2, loc=0, scale=1))
    t_b = stats.norm.ppf(1 - beta, loc=0, scale=1)
    

    mu_sqr = (mu - mu * eff) ** 2
        
    z_sqr = (t_a + t_b) ** 2
    disp = 2 * (std ** 2)

    sample_size = int(
        np.ceil(
            z_sqr * disp / mu_sqr
        )
    )
    return sample_size


alpha = 0.05
beta = 0.2

mu = 10
std = 1
effect = 1.005

groups = 5
comparisons = 10

n_values = list()

for i in range(1, comparisons):
    n_values.append(get_sample_size(mu, std, effect, alpha / i, beta))

print(f"Скорректированный объем выборки: {np.mean(n_values)}")

Получаем скорректированное значение sample size = 8986. На ~49% больше исходного значения минимального размера выборки.

Контроль средней ошибки II рода разными методами после коррекции sample size с учетом поддержания средней мощности

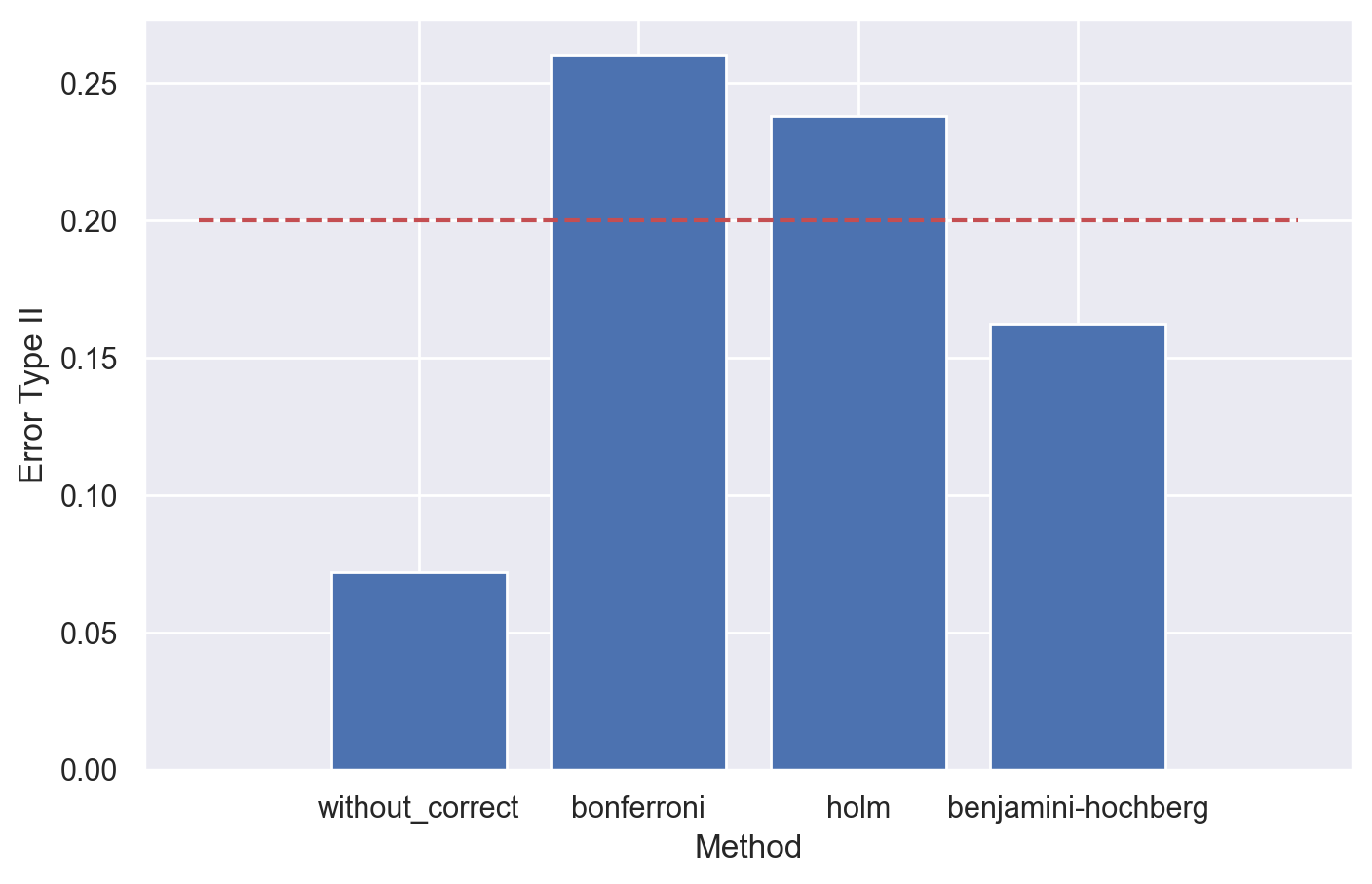
В таком случае ожидаемый уровень ошибок II рода для метода Холма несколько превышает заданный уровень 0.2, но может быть вполне приемлемым.

На практике при использовании методов контроля FWER (в том числе метода Холма) может быть более оптимальным использование поправки на размер выборки с учетом более консервативного метода коррекции $\alpha$ (первый вариант). Это будет гарантировать заданный уровень ошибок II рода.

Но стоит подчеркнуть, что для оценки мощности теста мы использовали среднее значение ошибки II рода, но для еще большей мощности также можем опираться на аналог FWER для ошибки II рода – вероятность допустить хотя бы одну ошибку II рода. Это потребует еще большего количества данных, но если у нас есть возможность собрать больше данных – почему бы не сделать тест мощнее.

Для примера скорректируем sample size с учетом вероятности допустить хотя бы одну ошибку II рода. Для этого мы также можем использовать, например, контроль средней ошибки II рода, в особенности при использовании метода Холма. В этом случае для надежности можно делить $\alpha$ не просто на количество сравнений, а на количество сравнений в квадрате, то есть в нашем случае на (это не обосновано математически, но получено опытным путем):

Код для коррекции sample size с учетом контроля аналога FWER для ошибки II рода

def get_sample_size(mu, std, eff=1.01, alpha=0.05, beta=0.2):
    """"""
    t_a = abs(stats.norm.ppf(alpha / 2, loc=0, scale=1))
    t_b = stats.norm.ppf(1 - beta, loc=0, scale=1)
    

    mu_sqr = (mu - mu * eff) ** 2
        
    z_sqr = (t_a + t_b) ** 2
    disp = 2 * (std ** 2)

    sample_size = int(
        np.ceil(
            z_sqr * disp / mu_sqr
        )
    )
    return sample_size


alpha = 0.05
beta = 0.2

mu = 10
std = 1
effect = 1.005

groups = 5
comparisons = 10

n_values = list()

for i in range(1, comparisons ** 2):
    n_values.append(get_sample_size(mu, std, effect, alpha / i, beta))

print(f"Скорректированный объем выборки: {np.mean(n_values)}")

Скорректированный минимальный объем выборки – 13К объектов, что ~в 2 раза больше исходного значения sample size.

Контроль вероятности допустить хотя бы одну ошибку II рода разными методами после коррекции sample size с учетом поддержания средней мощности

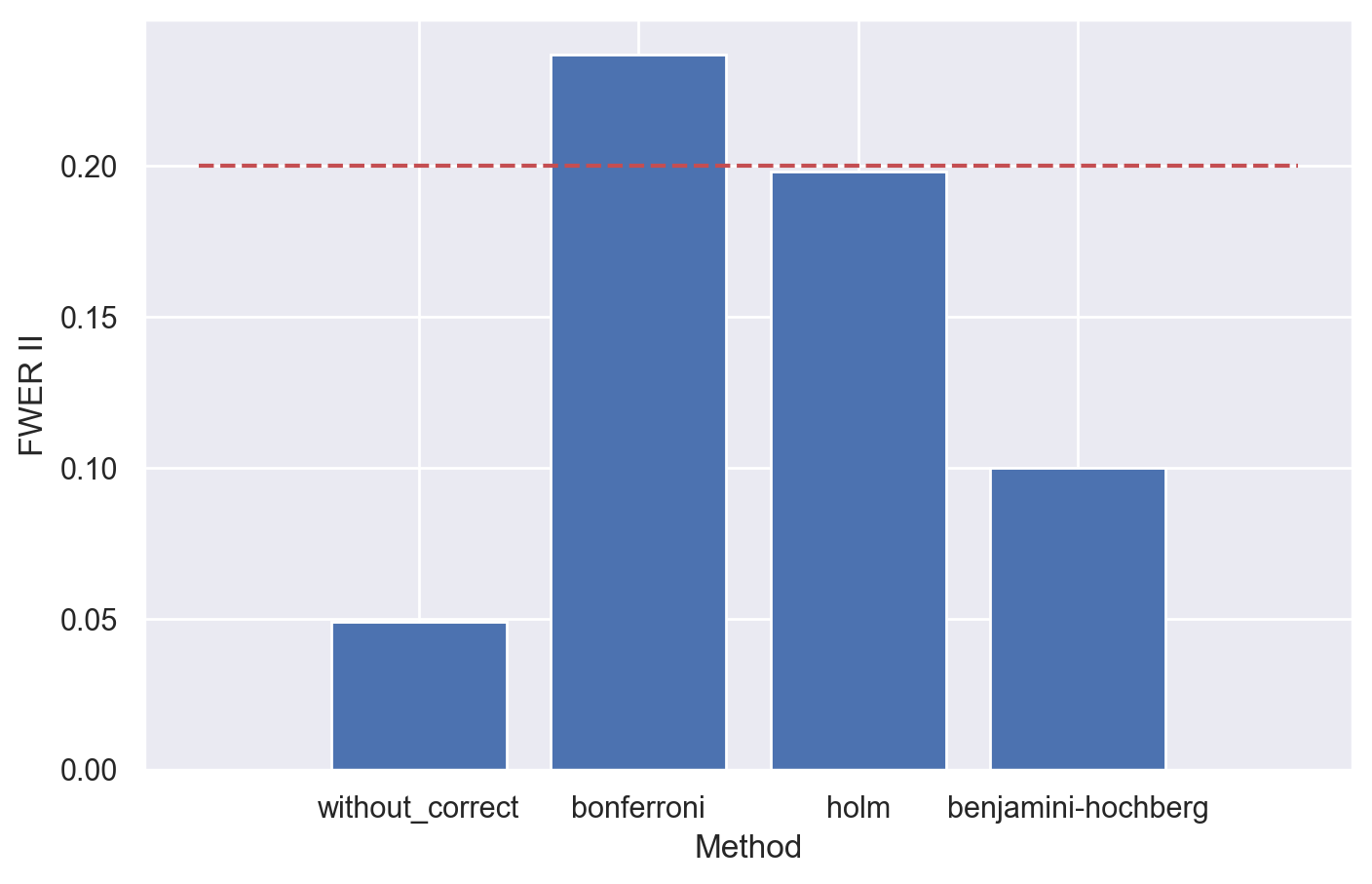
В таком случае для метода Холма мы будем контролировать вероятность допустить хотя бы одну ошибку II рода на заданном уровне, причем даже для метода Бонферрони ошибка сохраняется на приемлемом (хоть и выше заданного) уровне.

В примере мы делали поправку на множественное тестирование с использованием метрики FWER, но и при использовании FDR также можно корректировать минимальный объем выборки путем коррекции alpha при расчете sample size. Причем в случае использования FDR и поправки Бенджамини-Хохберга, понадобится добавлять гораздо меньше данных, чем в случае использования FWER.

Подведем итог:

На этапе дизайна эксперимента следует оценивать мощность теста с учетом выбранных поправок
Если хотим, чтобы мощность эксперимента при использовании поправок поддерживалась на заданном уровне, необходимо корректировать sample size
Если используем более мощные методы, например, Холма для контроля FWER или метод Бенджамини-Хохберга для контроля FDR, можем корректировать sample size с учетом контроля средней мощности эксперимента. При необходимости и возможности можем контролировать не просто среднюю ошибку II рода, а вероятность допустить хотя бы одну ошибку II рода (понадобится еще больше данных)
Если используем консервативные методы (метод Бонферрони), лучше корректировать sample size с наиболее строгим уровнем значимости

Когда еще может пригодиться множественное тестирование

Такого рода поправки можно использовать не только при планировании и оценки экспериментов с множеством групп, но и в других похожих случаях. Например, когда на этапе оценки экспериментов мы хотим обращать внимание сразу на несколько метрик (не редкий кейс, правда?). Изменения в рассматриваемых метриках не будут независимыми, так как они вызваны ходом эксперимента: в этом случае можно также корректировать p_value с учетом количества рассматриваемых метрик.