Слышали ли вы об «эффекте Даннинга-Крюгера»? Это (очевидная) тенденция неквалифицированных людей переоценивать свою компетентность. Обнаруженный в 1999 году психологами Джастином Крюгером и Дэвидом Даннингом эффект с тех пор стал очень знаменитым.
И вы понимаете почему.
Это слишком сочная идея, чтобы не быть правдой. Все «знают», что идиоты, как правило, не осознают своего идиотизма. Или, как выразился Джон Клиз :
Если ты очень-очень глуп, как ты можешь осознать, что ты очень-очень глуп?
Разумеется, психологи очень осмотрительны, что бы убеждаться, что доказательства воспроизводимы. Но, конечно же, каждый раз, когда вы их ищете, из данных выскакивает сам эффект Даннинга-Крюгера. Таким образом кажется, что все стоит на прочной основе.
Вот только есть проблема.
Эффект Даннинга-Крюгера также возникает из данных, в которых его не должно быть. Например, если вы тщательно обработаете случайные данные так, чтобы они не содержали эффекта Даннинга-Крюгера, вы все равно обнаружите этот эффект . Причина оказывается до неприличия простой: эффект Даннинга-Крюгера не имеет ничего общего с человеческой психологией. Это статистический артефакт — потрясающий пример автокорреляции.
Что такое автокорреляция?
Автокорреляция возникает, когда вы коррелируете переменную саму с собой. Например, если я измерю рост 10 человек, я обнаружу, что рост каждого человека идеально коррелирует сам с собой. Если это звучит как замкнутый круг рассуждений, то это потому, что так оно и есть. Автокорреляция — это статистический эквивалент утверждения, что 5 = 5.
В такой формулировке идея автокорреляции звучит абсурдно. Ни один компетентный учёный не станет соотносить переменную саму с собой. И это верно для чистой автокорреляции. Но что, если переменная окажется в обеих частях уравнения и забудется? В этом случае автокорреляцию обнаружить труднее.
Вот пример. Предположим, я работаю с двумя переменными: x и y . Я обнаружил, что эти переменные совершенно не коррелируют, как показано на левой панели рисунка 1. Пока всё нормально.
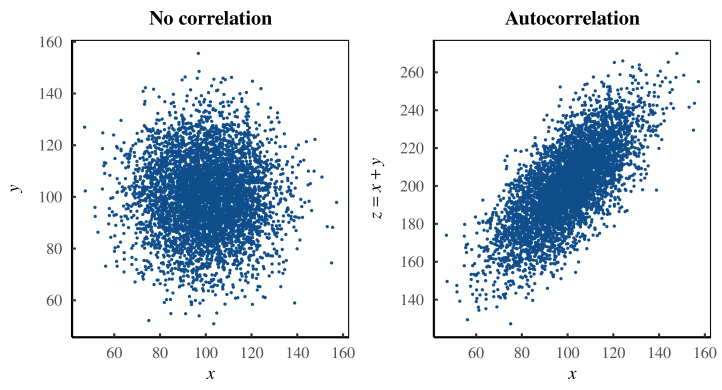
Далее я начинаю играть с данными. После некоторых манипуляций я получил величину, которую называю z. Я сохраняю свою работу и забываю о ней. Несколько месяцев спустя мой коллега вновь обращается к моему набору данных и обнаруживает, что z сильно коррелирует с x (рис. 1 , справа). Мы обнаружили кое-что интересное!
Фактически мы обнаружили автокорреляцию. Видите ли, без ведома моего коллеги я определил переменную z как сумму x + y . В результате, когда мы коррелируем z с x , мы на самом деле коррелируем x сам с собой. (Переменная y появляется в процессе, обеспечивая статистический шум.) Именно так происходит автокорреляция — забывая, что у вас есть одна и та же переменная по обе стороны корреляции.
Эффект Даннинга-Крюгера
Теперь, когда вы понимаете автокорреляцию, давайте поговорим об эффекте Даннинга-Крюгера. Как и в примере на рисунке 1, эффект Даннинга-Крюгера представляет собой автокорреляцию. Но вместо того, чтобы скрываться в измененной переменной, автокорреляция Даннинга-Крюгера скрывается под обманчивой диаграммой.
Давайте посмотрим.
В 1999 году Даннинг и Крюгер сообщили о результатах простого эксперимента. Они попросили группу людей пройти тест на навыки. (На самом деле Даннинг и Крюгер использовали несколько тестов, но это не имеет значения для моего обсуждения.) Затем они попросили каждого человека оценить свои способности. Даннинг и Крюгер (думали, что они) обнаружили, что люди, плохо сдавшие тест на навыки, также склонны переоценивать свои способности. Это «эффект Даннинга-Крюгера».
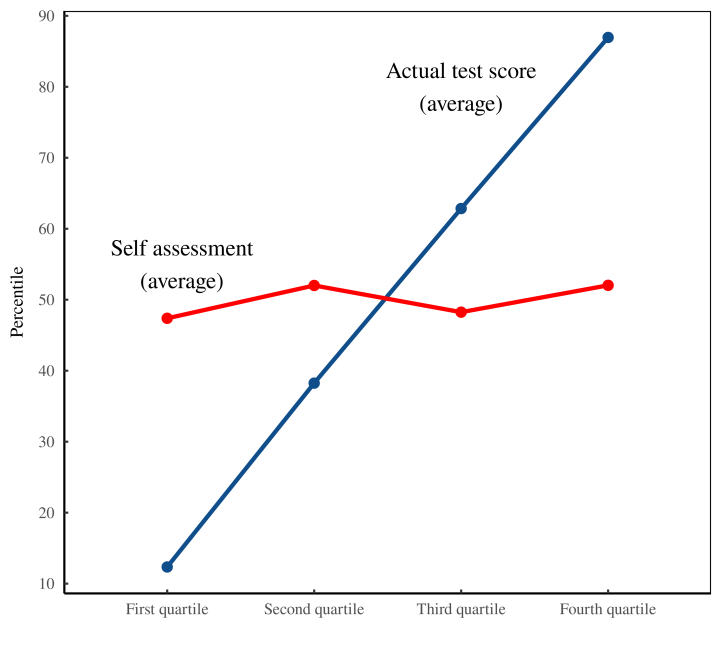
Даннинг и Крюгер визуализировали свои результаты, как показано на рисунке 2. Это простой график, который обращает внимание на разницу между двумя кривыми. На горизонтальной оси ученые распределили людей на четыре группы (квартили) в соответствии с их результатами тестов. На графике две линии показывают результаты внутри каждой группы. Серая линия обозначает средние результаты людей по тесту навыков. Черная линия указывает на их средние «воспринимаемые способности». Очевидно, что люди, получившие плохие результаты на тесте на навыки, слишком самоуверенны в своих способностях. (Или так кажется.)
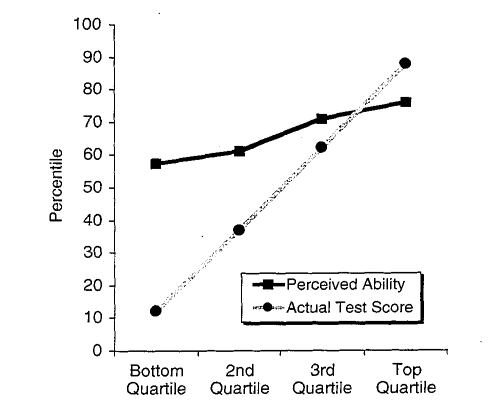
Сама по себе диаграмма Даннинга-Крюгера кажется убедительной. Добавьте к этому тот факт, что эти учёные — превосходные писатели, и вы получите рецепт хитовой статьи. В связи с этим я рекомендую вам прочитать их статью, поскольку она напоминает нам, что хорошая риторика — это не то же самое, что хорошая наука.
Разоблачение Даннинга-Крюгера
Теперь, когда вы ознакомились с диаграммой Даннинга-Крюгера, давайте покажем, как она скрывает автокорреляцию. Чтобы внести ясность, я буду комментировать диаграмму по ходу дела.
Начнем с горизонтальной оси. На диаграмме она является «категориальной», то есть на ней показаны «категории», а не числовые значения. Конечно, нет ничего плохого в использовании категорий. Но в данном случае категории на самом деле числовые. Даннинг и Крюгер берут результаты тестов людей и распределяют их по 4 ранжированным группам. (Статистики называют эти группы «квартилями».)
Это ранжирование означает, что горизонтальная ось эффективно отображает результаты тестов. Назовем эту оценку x .
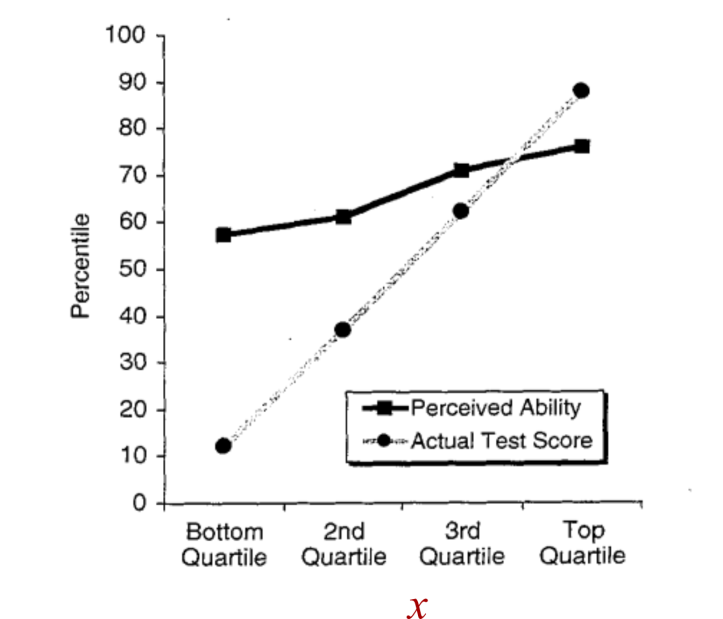
Далее давайте посмотрим на вертикальную ось, которая отмечена «процентилем» (Percentile). Это означает, что вместо того, чтобы отображать фактические результаты тестов, Даннинг и Крюгер строят рейтинг результатов по 100-балльной шкале.
Теперь посмотрим на кривые. В строке с надписью «текущий результат теста» (Actual Test Score) отображается средний процентиль результатов теста каждого квартиля (я знаю, что это непростая задача). Кажется, все в порядке, пока мы не осознаем, что Даннинг и Крюгер, по сути, строят график результатов теста ( x ) против самого себя. Заметив этот факт, давайте переименуем серую линию. Он эффективно строит график зависимости x от x.
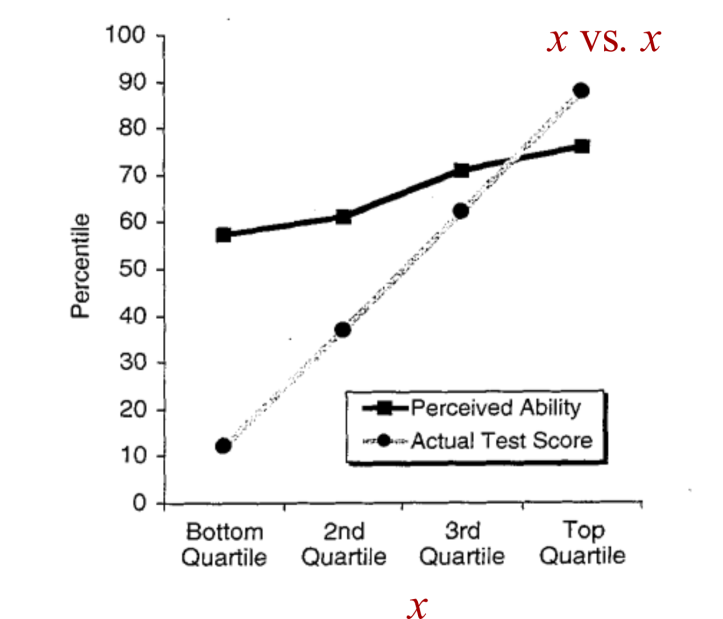
Двигаемся дальше, давайте посмотрим на линию «воспринимаемая способность» (Perceived Ability). Она отображает средний процентиль самооценки каждой группы. Назовем это самооценкой и. Вспоминая, что мы обозначили «фактический результат теста» как x , мы видим, что черная линия отображает зависимость y от результата x.
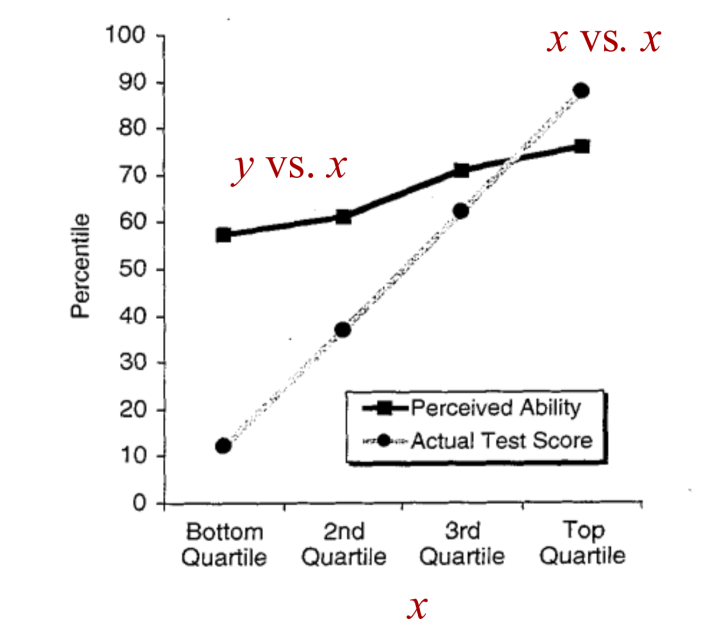
Пока ничего явно неправильного не выскакивает. Да, немного странно строить график x vs. x, но учёные не утверждают, что важна линия сама по себе. Что важно, так это разница между двумя строками («воспринимаемые способности» и «действительный результат теста»). Именно в этой разнице и проявляется автокорреляция.
В математических терминах «разница» означает «вычитание». Таким образом, показывая нам две расходящиеся линии, Даннинг и Крюгер (неявно) просят нас вычесть одну из другой: взять «воспринимаемые способности» и вычесть «действительный результат теста». В моих обозначениях это соответствует y – x .
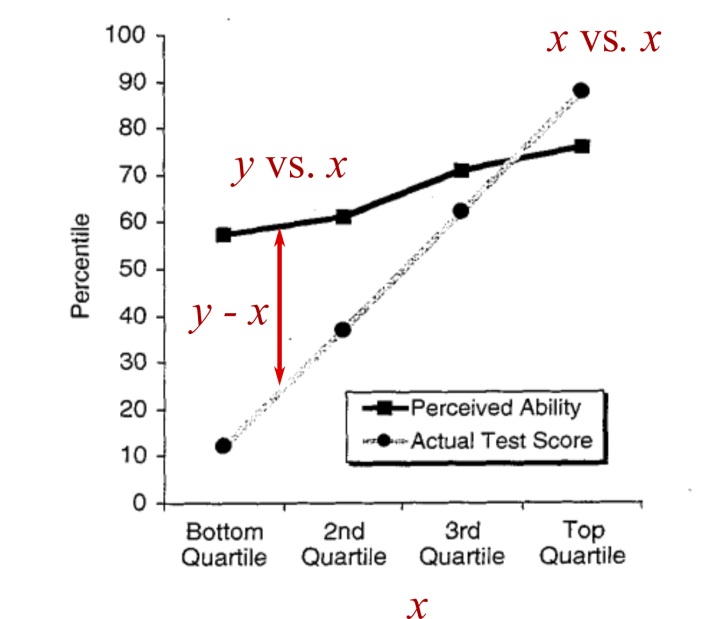
Вычитание y – x кажется вполне приемлемым, пока мы не осознаем, что должны интерпретировать эту разницу как функцию горизонтальной оси. Но по горизонтальной оси отложен результат теста x . Итак, нас (неявно) просят сравнить y – x с x :
(y−x) ∼ x
Видите проблему? Мы сравниваем x с его отрицательной версией. Это автокорреляция по учебнику. Это значит, что мы можем бросать случайные числа в x и y — такие, которые не содержат эффект Даннинга-Крюгера — и, тем не менее, на другом конце эффект все равно возникнет.
Воспроизведение эффекта Даннинга-Крюгера
Честно говоря, меня не особо убедили приведенные выше аналитические аргументы. Только используя реальные данные, я пойму проблему эффекта Даннинга-Крюгера.
Предположим, мы психологи, получившие крупный грант на повторение эксперимента Даннинга-Крюгера. Мы набираем 1000 человек, тестируем каждого из них и просим их пройти самооценку. Когда результаты будут получены, мы посмотрим на данные.
И выглядит это не очень хорошо.
Когда мы сопоставляем результаты тестов людей с их самооценкой, данные кажутся совершенно случайными. На рисунке 7 показан паттерн. Кажется, что люди с любыми способностями одинаково плохо предсказывают свои навыки. Нет и намека на эффект Даннинга-Крюгера.
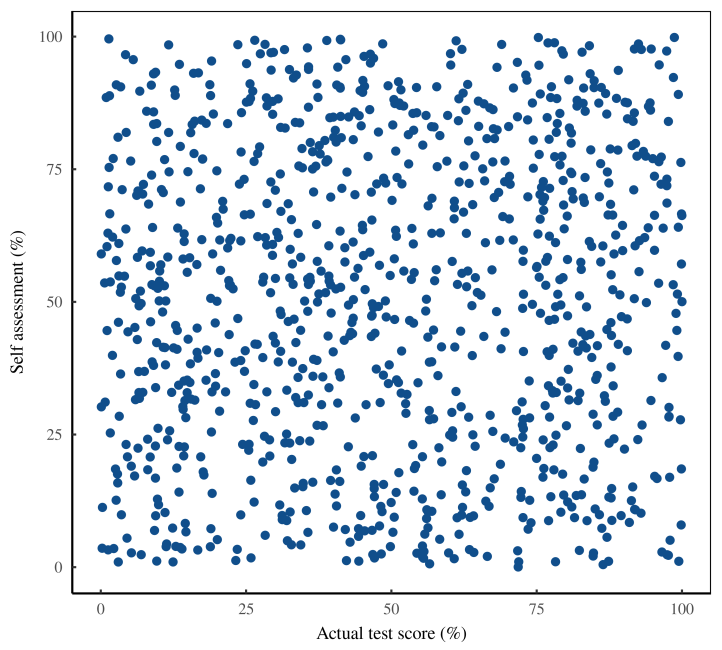
Посмотрев на наши необработанные данные, мы обеспокоены, что сделали что-то не так. Многие же другие исследователи повторили эффект Даннинга-Крюгера. Допустили ли мы ошибку в нашем эксперименте?
К сожалению, мы не можем собрать больше данных — у нас закончились деньги. Но мы можем поиграть с анализом. Коллега предлагает вместо построения необработанных данных рассчитать «ошибку самооценки» каждого человека. Эта ошибка представляет собой разницу между самооценкой человека и его результатом теста. Возможно, эта ошибка оценки связана с фактическим результатом теста?
Мы подсчитали цифры и, к нашему изумлению, обнаружили огромный эффект. На рисунке 8 показаны результаты. Кажется, что неквалифицированные люди чрезвычайно самоуверенны, а квалифицированные — чрезмерно скромны.
(Наши лабораторные специалисты отмечают, что корреляция на удивление тесная, как если бы числа были выбраны вручную. Но мы выбрасываем это наблюдение из головы и идем вперед.)
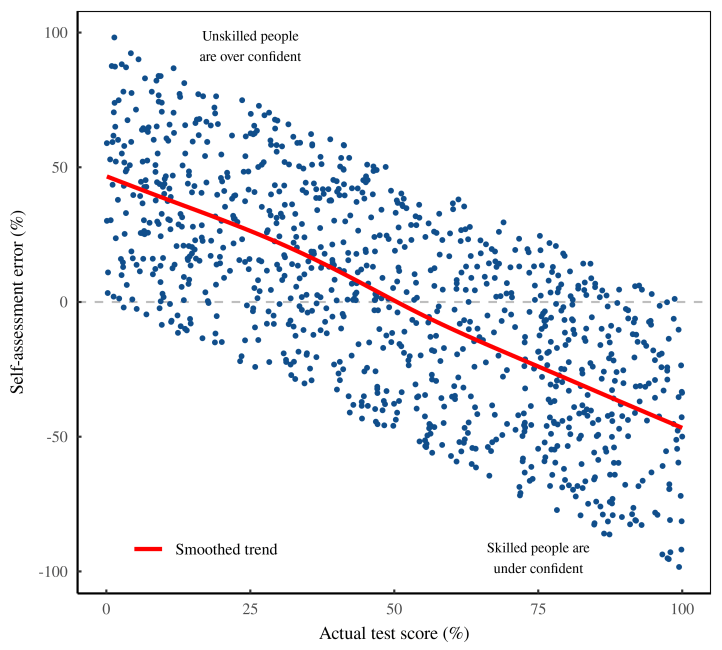
Воодушевленные успехом, мы решаем, что результаты, возможно, в конце концов не будут «плохими». Итак, мы строим диаграмму Даннинга-Крюгера, чтобы посмотреть, что произойдет. Мы обнаружили, что, несмотря на наши опасения по поводу данных, эффект Даннинга-Крюгера существовал всегда. На самом деле, как показано на рисунке 9, наш эффект даже больше, чем исходный.
Все идет под откос
Довольные нашим успешным воспроизведением, мы начинаем описывать наши результаты. И потом все разваливается. Охваченный чувством вины, наш дата инженер признается: он потерял данные нашего эксперимента и в приступе паники заменил их случайными числами. Наши результаты, признается он, основаны на статистическом шуме.
Опустошенные, мы возвращаемся к нашим данным, чтобы понять, что пошло не так. Если бы мы работали со случайными числами, как бы мы смогли воспроизвести эффект Даннинга-Крюгера? Чтобы выяснить, что произошло, мы перестаём притворяться, что работаем с психологическими данными. Мы переименовываем наши диаграммы в терминах абстрактных переменных x и y. Сделав это, мы обнаруживаем, что наш очевидный «эффект» на самом деле является автокорреляцией.
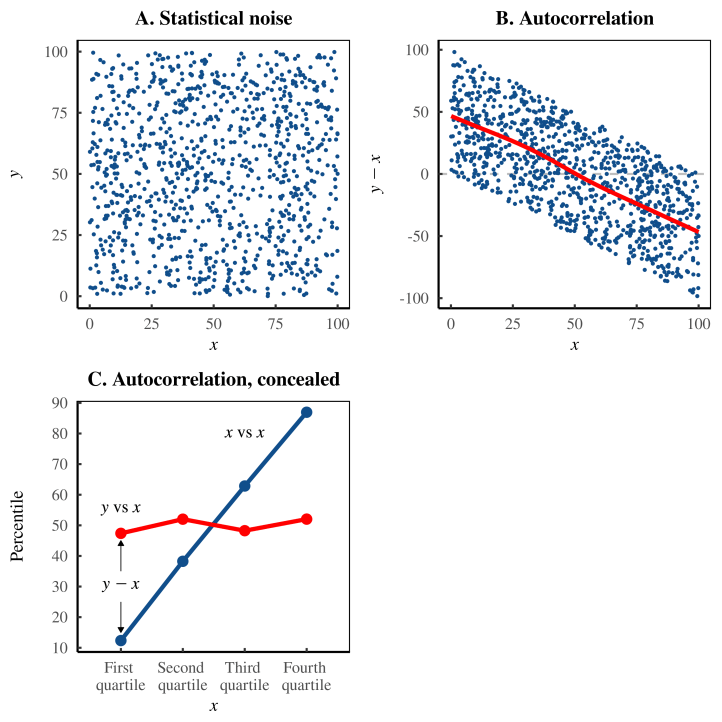
Рисунок 10 объясняет это. Наш набор данных состоит из статистического шума — двух случайных величин x и y, которые совершенно не связаны между собой (рис. 10 А). Когда мы вычисляли «ошибку самооценки», мы брали разницу между y и x . Неудивительно, что мы обнаружили, что эта разница коррелирует с x (рис. 10 B). Но это потому, что x автокоррелирует сам с собой. Наконец, мы разбираем диаграмму Даннинга-Крюгера и понимаем, что она тоже основана на автокорреляции (рис. 10 C). Он просит нас интерпретировать разницу между y и x как функцию x . Это автокорреляция из графика B, обернутая в более обманчивую оболочку.
Цель этой истории — продемонстрировать, что эффект Даннинга-Крюгера не имеет ничего общего с человеческой психологией. Это статистический артефакт — пример автокорреляции, скрывающийся на виду.
Что интересно, так это то, сколько времени потребовалось исследователям, чтобы осознать ошибку в анализе Даннинга и Крюгера. Даннинг и Крюгер опубликовали свои результаты в 1999 году. Но только в 2016 году ошибка была полностью понята. Насколько мне известно, Эдвард Нухфер и его коллеги были первыми, кто исчерпывающе развенчал эффект Даннинга-Крюгера. (См. их совместные статьи в 2016 и 2017 годах .) В 2020 году Жиль Жиньяк и Марсен Заженковски опубликовали аналогичную критику .
Как только вы прочитаете эту критику, станет до боли очевидно, что эффект Даннинга-Крюгера является статистическим артефактом. Но на сегодняшний день об этом факте мало кто знает. В совокупности три критические статьи цитируются примерно в 90 раз меньше , чем оригинальная статья Даннинга-Крюгера. Таким образом, похоже, что большинство учёных до сих пор считают, что эффект Даннинга-Крюгера является важным аспектом человеческой психологии.
Никаких следов эффекта.
Проблема с диаграммой Даннинга-Крюгера заключается в том, что она нарушает фундаментальный принцип статистики. Если вы собираетесь сопоставить два набора данных, их необходимо измерять независимо. В диаграмме этот принцип нарушается. На ней результаты тестов смешиваются по обеим осям, что приводит к автокорреляции.
Осознав эту ошибку, Эдвард Нухфер и его коллеги задали интересный вопрос: что происходит с эффектом Даннинга-Крюгера, если его измерить статистически достоверным способом? По свидетельству Нухфера, ответ заключается в том, что эффект исчезает.
На рисунке 11 показаны их результаты. Здесь важно то, что «навыки» людей измеряются независимо от их результатов на тестах и самооценки. Чтобы измерить «навыки», Нухфер группирует людей по уровню образования, показанному на горизонтальной оси. Затем вертикальная ось отображает ошибку в самооценке людей. Каждая точка представляет отдельного человека.
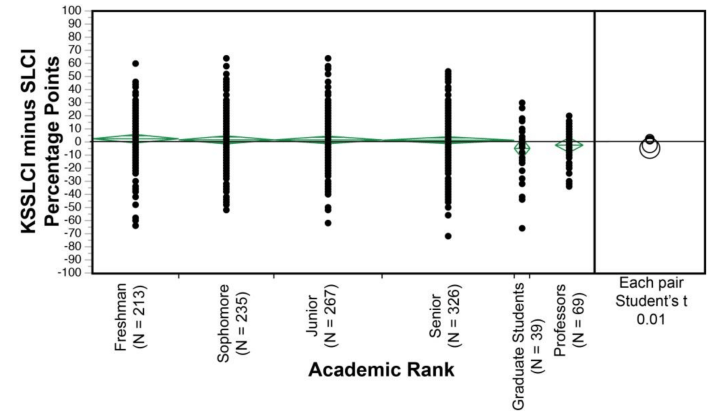
Если бы присутствовал эффект Даннинга-Крюгера, он отобразился бы на рисунке 11 как нисходящая тенденция данных (аналогично тенденции на рисунке 7). Такая тенденция указывает, что неквалифицированные люди переоценивают свои способности, и что эта переоценка уменьшается с увеличением навыков. Глядя на рисунок 11, мы не видим никаких намеков на тенденцию. Вместо этого средняя ошибка оценки (обозначенная зелеными кружками) колеблется около нуля. Другими словами, предвзятость оценки тривиально мала.
Хотя на эффект Даннинга-Крюгера нет никаких намеков, на рис. 11 показана интересная закономерность. Двигаясь слева направо, разброс ошибок самооценки имеет тенденцию уменьшаться по мере повышения уровня образования. Другими словами, преподаватели обычно лучше оценивают свои способности, чем первокурсники. В этом есть смысл. Обратите внимание, однако, что эта возрастающая точность отличается от эффекта Даннинга-Крюгера, который связан с системной погрешностью средней оценки. В данных Нуфера такой предвзятости не существует.
Неквалифицированный и не знающий об этом
Ошибки случаются. Поэтому в этом смысле нам не следует винить Даннинга и Крюгера в допущенных ошибках. Однако в обстоятельствах их ошибки есть восхитительная ирония. Вот два профессора Лиги плюща, утверждающие, что неквалифицированные люди несут «двойное бремя»: неквалифицированные люди не только «некомпетентны»… они не осознают своей собственной некомпетентности.
Ирония в том, что ситуация на самом деле обратная. В своей основополагающей статье Даннинг и Крюгер демонстрируют свою (статистическую) некомпетентность, смешивая автокорреляцию с психологическим эффектом. В этом свете название статьи может быть уместным. Просто именно авторы (а не испытуемые) были «неквалифицированными и не подозревали об этом».
Комментарии (70)

GospodinKolhoznik
26.11.2023 09:30+16Коллега предлагает вместо построения необработанных данных рассчитать «ошибку самооценки» каждого человека.
В этот момент у вас и появляется автокорреляция.
Но при чем здесь эффект Д.К. если у них зависимость самооценка/(результат тестирования тестов), а не (результат тестирования - самооценка)/(результат тестирования), как у вас?
Или это такой психологический эксперимент, чтобы проверить, насколько аудитория Хабра критично воспринимает информацию?

kompilainenn2
26.11.2023 09:30+28эта статья - это подтверждение того самого эффекта, который пытается опровергнуть

Gorthauer87
26.11.2023 09:30Так а не это ли означает, что данный эффект неопровержим?

no404error
26.11.2023 09:30Это означает что статья написана придурком для придурков. Ни подтверждений, ни опровержений, а только некие высосанные из пальца факты и доводы.
Хотите утвердиться в научном мире - подтвердите теорию практикой. Хоть на минимальном уровне, пускай даже нерепрезентативном. Пускай клоп будет вашим свидетелем.
Общий смысл статьи заключается в типичной для "ньюби" мира: Выборка это то, что мне нужно, остальное - отрицаем. Пардон, но так и евклидову геометрию по***ить можно. Или тут речь о том, что "Бастилию брал не я, но как найду, то положу на место?"

avdx
26.11.2023 09:30Потому что на основе одного графика никаких выводов сделать нельзя. А выводы о наличии эффекта делаются на основе совместного анализа двух графиков, конкретно их разницы: если разница больше нуля - переоценка, меньше нуля - недооценка.

IlyasA74
26.11.2023 09:30+3Хабр - это не научный журнал и, соотвественно, аудитория Хабра - не аудитория научного журнала. Если бы автор перевода потрудился хотя бы просмотреть оригинальную работу 1999 г. гг. Даннинга и Крюгера, он бы выбрал другую статью для перевода.

agray
26.11.2023 09:30+2Ничего не понял, но кажется теперь я не тупой! Ура! Ох уж этот Даунинг-Крюгер, как же он ошибался.

ImagineTables
26.11.2023 09:30Не хочу огорчать, но он, вроде как, говорит, что тупые могут быть неуверенными в себе, а умные — самоуверенными.

Aniro
26.11.2023 09:30+19Цель этой истории — продемонстрировать, что эффект Даннинга-Крюгера не имеет ничего общего с человеческой психологией. Это статистический артефакт — пример автокорреляции, скрывающийся на виду.
Подождите. На приведенном графике хорошо видно что это не так. Эффект далеко за пределами статистической погрешности и заключается он в том что самооценка человека и его реальные результаты теста хотя и не являются полностью независимыми, но кореляция между ними существенно меньше единицы. В этом и заключается эффект - люди ошибаются в своей самооценке и благодаря склонности к излишнему оптимизму сильнее ошибаются люди с худшими реальными результатами.
Рассмотрим ваш гипотетический случай с отсутствием кореляции между самоценкой и результатом. Если бы был реальностью, он бы говорил о том что люди вообще неспособны оценить свои работы самостоятельно.Двигаясь слева направо, разброс ошибок самооценки имеет тенденцию уменьшаться по мере повышения уровня образования. Другими словами, преподаватели обычно лучше оценивают свои способности, чем первокурсники
И.. вы сами описали здесь эффект Даннинга-Крюгера - более компетентные люди лучше оценивают свои реальные сопособности. Это буквально тоже он.

dimitrii_z
26.11.2023 09:30+4Лучше оценивают, но не переоценивают. Изначально была речь о переоценке вроде:
Слышали ли вы об «эффекте Даннинга-Крюгера»? Это (очевидная) тенденция неквалифицированных людей переоценивать свою компетентность.

ef_end_y
26.11.2023 09:30А те, кто хуже себя оценивают, они переоценивают или недооценивают? Или на одном уровне?

muxa_ru
26.11.2023 09:30+9И.. вы сами описали здесь эффект Даннинга-Крюгера - более компетентные люди лучше оценивают свои реальные сопособности. Это буквально тоже он.
Нет.
Обсуждаемый "эффект" гласит не то что "глупые оценивают себя неправильно", а "глупые считают себя умнее чем есть на самом деле".

Aniro
26.11.2023 09:30Это какое-то очень вульгализированное определение. Вот вики: "The Dunning–Kruger effect is a cognitive bias in which people with limited competence in a particular domain overestimate their abilities. Some researchers also include the opposite effect for high performers: their tendency to underestimate their skills."
Люди с низкой компетентностью переоценивают свои способности, люди с высокой - недооценивают. Никаких "глупых" и "умнее" тут нет.

sanitareugen
26.11.2023 09:30+6Разоблачён только секрет популярных блогеров - рассуждать о том, чего не понимаешь, но читатель тоже не понимает, но поддаётся уверенному тону и "открытию тайн".
Для начала - автокорреляция это совсем другое.

kenoma
26.11.2023 09:30+4Человек пытался на пальцах объяснить, что сравниваются две переменные x и производная из нее, условный x+y. Естественно, между ними будет наблюдаться высокая степень скоррелированности. На практике обычно это означает, что совместное рассмотрение таких двух переменных нового знания не дает, о чем и написано в этой статье.

Radisto
26.11.2023 09:30+5Прошу прощения, что-то я не понял: человек демонстрирует эффект Даннинга-Крюгера, пытаясь его опровергнуть, или нет? Я запутался

haldagan
26.11.2023 09:30+4Читал по диагонали и что-то ваши аргументы насчет автокорелляции меня не убедили (начиная с момента "предположим мы получили вот такие вот рандомные данные").
Если бы мне вдруг захотелось разоблачить эффект Даннинга-Крюгера, то я бы просто заявил, что "люди в среднем считают себя выше среднего" и сказал бы, что это связано с этим и вот этим

vvbob
26.11.2023 09:30Есть некоторая методика, которая демонстрирует некий эффект, "закон". Если даем ей на вход корректные данные - она хорошо демонстрирует эффект, если подсовываем ей случайный набор данных, то она.. тоже так-же хорошо демонстрирует этот эффект. Как по нме методика явно никуда не годится, если она вне зависимости от корректности данных дает один и тот-же нужный авторам эффект.

ksbes
26.11.2023 09:30+1Неверный вывод.
С чего вы взяли что независимые случайные данные - некорректные?
То, что эффект является следствием независимости величин - не делает эффект "неправильным".
Особенно когда нулевая гипотеза - что величины как раз-таки зависимы.
vvbob
26.11.2023 09:30А с чего вы решили что они корректные? Случайные величины страдают синдромом Данинга-Крюгера? Так что-ли?

Kergan88
26.11.2023 09:30Случайные величины страдают синдромом Данинга-Крюгера? Так что-ли?
Именно так)
Нулевая гипотеза предполагает, что коэффициент регрессии для зависимости самооценки от актуальной оценки должен быть близок к единице. Это поведение, которого мы ожидаем от людей. Если мы получаем отклонение - то, значит, есть какой-то эффект, который это отклонение вызывает (люди ведут себя не так, как мы ожидаем). В случае со случайными величинами - мы явно не можем ожидать, что люди в качестве своей оценки будут давать просто случайное число (будто бросают кубик). И если наши данные выглядят, будто они делают именно так - то есть какой-то эффект, который должен обеспечивать подобную статистику. Почему выглядит так, что люди отвечают случайно, хотя мы-то точно знаем, что они отвечают неслучайно? Вот причина, по которой так происходит - это и есть эффект Даннинга-Крюгера.

Aniro
26.11.2023 09:30+1Но результаты в зависимости от разных входных данных разные. Возьмем три набора данных. Реальные, независимое случайное распределение, прямую кореляцию при которой самооценка равна реальному результату.
Получим для реальных данных коэффициент кореляции ~0.5; для случайного распределния ~0.0; для прямой кореляции =1.0 (внезапно)
Выводы:
люди в среднем способны оценивать свою компетентность; (иначе коэффициент был бы как при случайном распределении)
люди обычно неверно оценивают свою компетентность; (иначе коэффициент был бы как при прямой корреляции)
абсолютная ошибка оценки выше на низких уровнях компетенции; (это не следует из приведенных наблюдений, но следует из реальных данных)

ABRogov
26.11.2023 09:30+5Итак, нас (неявно) просят сравнить y – x с x :
(y−x) ∼ x
Видите проблему? Мы сравниваем x с его отрицательной версией.
Если бы в этой разнице, автокорреляция играла бы решающую роль, то наклон всего графика был бы обратный. Ведь x коррелирует с -x. А на графике наклон положительный.

hurrdurrrderp
26.11.2023 09:30+5Спасибо за перевод, очень интересно! Когда я понял, что весь эффект сводится к утверждению "с ростом x значение y-x уменьшается", я полез пересматривать график ещё раз - не может же быть всё так тупо! Оказалось, что может.

hurrdurrrderp
26.11.2023 09:30+3Перечитал статью и критику в оригинале:
1) То, что эффект воспроизводится на случайных данных, его не опровергает, а скорее подтверждает, пусть и не в особо сильном виде (это по сути равносильно ситуации, где оценка своих способностей никак не связана с реальной компетенцией).
2) Эффект всё равно подтасован из-за проблем с неравномерным обрубанием шума в данных на концах разброса (для худших и лучших). Написал в другом комментарии ниже объяснение подробнее.

sci_nov
26.11.2023 09:30+1Я думаю, что никакого подвоха нет: в целом, тесты проверяют способности человека объективнее, чем сам человек, однако, с ростом человека его оценка может становиться точнее.
Здесь две степени свободы: человеческий решатель и решатель-тест. Между ними есть некоторая корреляция, именно честная, которую и должна ловить наука. Пример - связь тока и напряжения в электрической цепи. Это две степени свободы, потому что напряжение не всегда влечет за собой ток - это зависит от сопротивления цепи, и наоборот.

Andy_U
26.11.2023 09:30Да какая нафиг корреляция между категориальной и непрерывной переменными? Тут надо дисперсионный анализ применять

ABRogov
26.11.2023 09:30+1Квартили это количественная оценка. Дискретность не мешает корреляции с непрерывным. Например так часто делают при калибровке АЦП. Напряжение подают "аналоговое", а результат берут в цифровом бинаризированном виде.

Andy_U
26.11.2023 09:30Например так часто делают при калибровке АЦП
Оттого, что часто что-то делают, оно не ставновится правильным в научном смысле.

CorwinH
26.11.2023 09:30+19На рисунке 2 (жирная кривая) видно, что самооценка очень слабо коррелирует с результатами тестов. То есть, люди с низким результатом тестов в среднем оценивают себя почти так же, как люди с высоким результатом тестов. Ну а раз они оценивают себя почти одинаково, то люди с низкой квалификацией склонны переоценивать себя, а люди с высокой квалификацией - недооценивать. (Предполагаем, что результаты тестов коррелируют с уровнем квалификации).
Далее в статье продемонстрировано, что если взять две независимых случайных величины, то график получится почти такой же (красная горизонтальная кривая на рисунке 10). И это только подтверждает первоначальный вывод, что самооценка очень слабо коррелирует с результатами тестов.

Apxuej
26.11.2023 09:30+1Допустим человек случайно оценивает свой результат теста: вероятность попасть в группу "переоценки собственных результатов" у тех кто прошёл тест отвратительно почти 100%, также и у тех кто прошёл тест идеально и случайно оценивает свой результат почти 100% вероятность попасть в группу "недооценки собственных результатов". Т.е. если оценка людьми своих способностей случайна, то они не "склонны", у них нет выбора. Т.е. человеку набравшему 0/100 на тесте нужно в своей оценке попасть в диапазон от 0 до 25 (25% диапазона), чтобы сравниться по точности с человеком набравшим 50/100 и который в своей оценки попадает в диапазон от 25 до 75 (50% диапазона), мало того у "неуспевающего" с 0/100 в тесте нет физической возможности недооценить свой результат, только переоценить или угадать идеально точно, у "отличника" 100/100, та же ситуация только с обратной стороны. Единственно верный вывод из реальных тестов: "люди с низкой квалификацией немного менее точно оценивают свои результаты (как в меньшую, так и большую сторону) по сравнению с людьми с высокой квалификацией".

buriy
26.11.2023 09:30+7Давайте лучше опишу так, что вы сможете пересказать своим друзьям, которые не знают, что такое коэффициент корреляции и линейная регрессия.
1) Набираем 5 человек в группу. Тестируем их с помощью 100-балльного теста, получив результаты 30, 40, 50, 60, 70 (неважно в каком порядке, важно лишь, что результаты теста распределяются не от 0 до 100 равномерно, а блже к среднему).
2) Теперь допустим эти люди назвали оценки своих тестов, ошибившись на 2 балла в обе стороны равномерно, ну скажем: 32, 41, 49, 59, 71 .
3) Теперь эти два профессора зачем-то теперь переранжировали результаты тестов по 100-балльной шкале от 0 до 100, получив в нашем примере цифры 10, 30, 50, 70, 90 .
4) Теперь они вычитают переранжированные результаты тестов и собственную оценку результатов тестов этими людьми. В данном примере получается, что тот, кто оценил себя на 32 балла, получил на самом деле 10 баллов на тесте (на самом деле -- на переранжированном тесте!), то есть, накрутил себе 22 балла! А тот, кто набрал 90 баллов (опять же на переранжированном тесте!) -- оценил себя на 71 балл, а набрал 90 баллов, то есть, наоборот, на 19 баллов оценил себя хуже. И такой результат статистически значимый, и выглядит как почти прямая наклонная линия.
5) Делаем вывод: те люди, что хуже сдают тест -- накручивают себе результаты, а те, что лучше сдают тест -- занижают свои результаты. Причём весьма сильно. Видите же какой большой наклон у линии?
6) ... (стыдное немое молчание в зрительском зале, потому что ни один психолог, который читал их работу, за 17 лет с 1999 по 2016 год не заметил этот хитрый математический трюк! А математики, видимо, эту работу и не читали вовсе)
7) Профит!

Stiver
26.11.2023 09:30+1В 3) также проводят аналогичный перерасчет самооценок. У серой и черной линий шкала Y одинаковая, естественно, иначе на графиках творились бы Содом и Гоморра. Особенно если учесть, что изначальные оценки тестов не обязательно числовые.

hurrdurrrderp
26.11.2023 09:30+4Если я правильно понял, то весь прикол в том, что в таком переранжированном варианте те, кто в топе, просто физически не могут себя сильно переоценить. Даже если человек набрал 40 баллов из 100, но при этом среди всех n участников эксперимента это лучший результат, то он не может оценить себя выше чем на n (потому что их спрашивают о том, как они справились относительно других, а не "сколько баллов вы набрали по вашему мнению"). А в меньшую сторону себя недооценить можно хоть на n-1. Аналогичная проблема с теми, кто в самом низу - они могут себя только переоценить. Как можно получить другой результат с такими измерениями? (риторический вопрос)

D7ILeucoH
26.11.2023 09:30+1За пример конечно респект, но всё же не кажется ли тебе неправильным "хитрую" работу с ошибкой? Ведь 2 балла от 30 и 70 это более чем в 2 раза разные значения, при этом ты увеличил разницу взяв 32 и 71. О чём я говорю: величина отклонения для сравнения при заданных двух баллах - кажущимися как 2%:
2/30≈6.67% и 1/70≈1.4% соответственно. То есть сам разброс опорных данных отличается как минимум в 4 раза.
Если за начальное условие брать то, что участники уже знают с округлением до десятков свой результат — величину ошибки следовало бы как-то привязать к самому результату (хотя бы шумному). Хотя лично мне кажется что эффект ДК наблюдается именно в попытках людей правильно определить десятки - ментально на уровне сравнения "я точно знаю лучше того ботаника"

Vsevo10d
26.11.2023 09:30+1А вы знакомы с непараметрическими статистическими критериями? Там, в отличие от всеми любимого t-критерия, значения вообще не имеют значения (извините). Пусть у вас экспериментальные точки будут равны 1, 2, 27, 80, 5, 31, 100, 2000, 800, 10 - любой ранговый критерий их располагает в порядке от 1-го до 10-го и над ними уже проводит поранговое сравнение выборок. И это работает.

CorwinH
26.11.2023 09:30Тестируем их с помощью 100-балльного теста, получив результаты 30, 40, 50, 60, 70
После этого их спрашивают, как Вы оцениваете свои знания по сравнению с другими. Тот, кто набрал 30 баллов, отвечает "мои знания выше среднего" (58% на графике на рис.2). Не смотря на то, что другие показали результат выше, чем у него.

Kodim
26.11.2023 09:30Как из п.1 получили числа в п.3, поясните, плз

buriy
26.11.2023 09:30+1Переранжировка -- это когда мы берём результаты теста, и наихудшему даём значение 1, следующему -- значение 2, дальше 3, 4, и так далее до 100.
Если человек 5, а не 100, то чисел на всех не хватает, поэтому они берут равноудалённые точки на прямой линии от 0 до 100, например, если у них 4 когорты, то одной когорте они приписали значение 15, второй 40, третьей 65, четвёртой 90 ( то есть, 10 + 25*n ).
ABRogov
26.11.2023 09:30Там использовались квартили, то есть интервал разбивался равномерно, а не просто по порядку. Грубо говоря, интервал 50-60-70-80 перевели в 10-30-60-90. При этом, например 54 попало бы в первый бин. А по вашему, стало бы больше бинов.

Stiver
26.11.2023 09:30+10Кто-то где-то в интернете ляпнул чушь и теперь ее везде обсуждают. Хотя статья сама по себе хороша, можно дать в старших классах с заданием объяснить, что именно в ней неверно (помимо того, что автор под автокорреляцией понимает, видимо, что-то глубоко свое и отличное от остального мира).
В двух словах: автор утверждает, что если самооценка человека будет полностью случайной (горизонтальная красная линия), то мы увидим похожий эффект - худшие оценивают себя лучше, лучшие хуже.
А значит все врутСпасибо, это в общем-то тривиально (смещение к среднему). Соль как раз в том, что самооценка человека ожидается быть не случайной, а где-то в тесной окрестности его реальной оценки, чего не происходит. И вот это расхождение ожидания с наблюдением и назвали эффектом.Желающие могут еще на HN посмотреть, там народ тоже поудивлялся: https://news.ycombinator.com/item?id=38415252

Kergan88
26.11.2023 09:30+6>Кажется, что люди с любыми способностями одинаково плохо предсказывают свои навыки. Нет и намека на эффект Даннинга-Крюгера.
Вот здесь и есть ваша ошибка. Из графика видно, что способные и неспособные дают одинаковую оценку своим навыкам - а это автоматически означает, что способные себя недооценивают, а - неспособные - переоценивают. То есть наблюдается тот самый эффект. Иными словами - эффект даннинга-крюгера заключается как раз в том, что ожидаемой корреляции нет (ну точнее на вашем теоретическом графике нет - на практике она есть, но существенно ниже ожидаемой).

Vsevo10d
26.11.2023 09:30У меня почему-то на месте, где автор объяснял автокорреляцию, возникло полное непонимание, что он имеет в виду, и одновременно было стойкое ощущение, что он этого не понимает тоже.
Доб.: а-а, подождите. Так на графиках все видно. Он процентиль самооцениваемых способностей считает РАЗНИЦЕЙ х и у, то есть, величиной, имеющей ту же размерность, что и х (баллы в тесте), хотя процентиль - это безразмерная ранжированная величина, а вот квартили по абсциссе - это условные дискретные группы, все же привязанные к физическому значению (килограммы, метры, баллы теста). Вот в чем его лажа. Я прав?

rg_software
26.11.2023 09:30+3Стоит отметить, что формулировка "неквалифицированные люди переоценивают свои способности, а квалифицированные люди слишком скромны" вряд ли заслуживает такого количества упоминаний к месту и не к месту. Куда чаще "эффект Д-К" вспоминают в ситуации условного дурака, который считает себя умнее специалиста. Но вот это как раз пример чистого народного творчества: ни из статьи, ни из графиков не следует, что неспециалист считает себя лучше специалиста. Он, максимум, считает себя более компетентным, чем он есть на самом деле.

ksbes
26.11.2023 09:30+1Я нередко встречаюсь со второй его частью - что хорошие специалисты себя склонны недооценивать.
Т.е. самооценка неспециалиста может и нередко на практике совпадает или выше, чем самооценка неспециалиста.
Иными словами, из опыта мелкого руководителя - бесполезно спрашивать у человека что он умеет: надо "бросать в в воду" и внимательно следить как он "плывёт" (либо, что происходит чаще - просто поспрашивать тех, кто с ним работал).
SergioT4
26.11.2023 09:30Я знаю, что ничего не знаю
Надо наверное откалибровать шкалу оценки знаний, прежде чем сравнивать специалиста и неспециалиста. Хороший специалист может давать оценку своим знаниям с учётом глубины своего знания.
А неспециалист, следовать правилу, что себя надо оценивать как можно лучше, тогда вдруг нахаляву плюшек отсыпится.
Было бы интересно попробовать сделать исслевдование, где группа специалистов, которые совместно поработали, ранжировали всех внутри группы, тогда можно было бы лучше видно если хорошие специалисты себя недооценивают.

economist75
26.11.2023 09:30+1Статья понравилась, хотя данных для размышления не хватило. Автокорреляция в ДК есть хотя бы потому что показ знания и их условная оценка осуществляются одним лицом - респондентом.
Но есть и психология. Безо всякой статистики, крайние представители общества (маргиналы-двоечиники и ботаны-отдличники), находясь у "краев" данных просто дают скос самооценки. Двоечник не поставит себе 1 или 0, а отличник не поставит себе 6. Да и 5 в силу ботанячей скромности тоже поставит себе не всякий.
Если бы товарищи Д. и К. предприняли обыденные в наше DS-время техоперации по устранению скоса и провели заново тесты на статзначимой выборке, с психподготовкой респондентов вида "как вы оцениваете свои навыки применительно к сфере вопросов", - они бы не получили "сенсацию". Всего этого не было, и мы получили новую офисную религию. И ведь страшно то что в больших корпорациях эффект ДК становится элементом HR-политики, хардкодится в KPI и системы тестирования итд.
Увы, если ученые (особенно в тандеме) ловят хайп идеи на острие пера - все их дальнейшие усилия будут направлены на подтверждение, а не критику своей идеи, и в этом они преуспеют. Именно за этот счет существуют инфоцыгане, "врачеватели" и т.п. публика. В целом это не плохо и не хорошо, потому что позволяет помнить о наличии оценок 0 и 6 (в терминах DS - NaN и Infinity) в пятибалльном мире.

RomeoGolf
26.11.2023 09:30+5Я, конечно, социолог не настоящий, но по опыту общения хочу сказать, что упомянутый эффект этот наблюдается, но сильно зависит от области знания. Как известно, в футболе и медицине у нас разбираются все. Еще ни разу не встречал, чтобы условный пролетарий (слесарь или токарь) переоценивал свои знания в математике или физике, скорее, наоборот, скажет, что вообще ничего не помнит и не знает, хотя если напряжется - и теорему Пифагора докажет, и квадратное уравнение решит. Зато каждая домохозяйка точно знает, когда надо назначать антибиотики. Большая разница между теми областями, где ошибку можно указать почти сразу, пользуясь справочниками или элементарно калькулятором, и теми, где для правильного ответа вообще может быть в принципе недостаточно данных, типа истории или медицины, и нет возможности показать: смотри, на самом деле правильно было не так, а так.
Особенно это заметно в области управления, где результат зависит далеко не только от принимающего решения. Если слабый руководитель с хорошей командой примет неверное управленческое решение, команда может выправить ситуацию вопреки, а не благодаря его действиям. Руководитель же решит, что он все правильно сделал - результат-то отличный! После нескольких подобных действий команда будет фильтровать информацию, подаваемую руководителю, даже врать, предвидя возможные решения, которые опять придется расхлебывать. А результат все лучше, и руководитель растет... Ошибочной может быть не только его самооценка, но и оценка со стороны по результатам, хотя изнутри команды большинство в курсе. С такими ситуациями был знаком не понаслышке. При этом многие толковые и харизматичные личности, которые реально могут хорошо управлять (о чем говорит их лидерство во временных командах), не уверены, что у них получится и не хотят командовать. Линейному же специалисту довольно быстро становится ясно, насколько часто он ошибается, отсюда он может неплохо скорректировать самооценку.
Так что при математическом подтверждении подобного эффекта не мешало бы учитывать такую особенность, все таки компетентность в лингвистике или математике - сильно разные вещи...

afedorenko888
26.11.2023 09:30+1дилетантам просто не хватает когнитивных навыков, чтобы определить свой истинный уровень некомпетентности)

jaqjaq
26.11.2023 09:30Как учитываются оценки людей, которых оценивают по знаниям в биологии, они в ней не разбираются, но при этом доктора наук философии/архитектуры/истории? Я не думаю, что их самооценка будет сильно завышена, скорее наоборот. И как мне кажется, «двоечники», которые вообще ни в чем не разбираются, тоже будут оценивать себя как «я дурак». А заметны обычно «среднячки» с завышенной самооценкой, воинствующая серость.

elishagg
26.11.2023 09:30+2А как тогда быть с эффектом самозванца? Это ведь полностью обратная сторона медали.
Да, конечно, это чисто психологическая проблема человека, однако!...
Если мы возьмём область знаний как окружность, то расширение данной окружности неминуемо ведет к увеличению периметра соприкосновения с непознанным.
Таким образом, теория обратная от эффекта Даннига-Крюгера является вполне жизнеспособной.

phenik
26.11.2023 09:30+2Это может происходит с любыми субъективными оценками, на то она и психология) см. например, оценку и самооценку IQ, и заодно обсуждение этой темы на вики.

MiyuHogosha
26.11.2023 09:30+1эффект Даннинга-Крюгера - это название метакогнитивное искажения, механизма существующего для объяснения того самого несоответствия. То есть существует он только в субъективном восприятии. Личность не является случайным набором данных\параметров, они взаимосвязаны.
Проблема в том, что и любое тестирование знаний также подвержено субъективности. И достоверность проверки знаний падает при снижении объемов знаний тестируемых. Тестирование, в том числе, подверженно ограничению знанием тестирующего. Вне экзаменов это в выливается в тот факт, что некомпетентность не всегда оценивается объективно. Самооценка тем более субъективна.
По ЭДК написано очень много, сравнение с автокорреляцией и аргументы против нее(т.к. сам постулат полагается на проведение исследований, также обладающих автокорреляцией) уже проводилось несколько лет назад. Но не первоисточником данной статьи.

larasage
26.11.2023 09:30+2Глядя на "зелёные пузыри" рисунка 11 неожиданно понимаешь, что Д-К были правы: у менее компетентных средние субъективные значения выше объективных, у более компетентных - ниже.

Andruh
26.11.2023 09:30+3Да не там никакой автокорреляции, даже если вы увидели формально в формуле x и там и там.
Есть две независимые величины: реальный скилл и оценка скилла респондентом. Только они и нарисованы. Всё.
Мы можем заключать: профаны оценивают себя середнячками.
Эксперимент со случайными данными на самом деле сильно похож на реальность. В реальности также примерно любого скилла человек оценивает себя случайно от 0 до 100 - получается то что получилось. У Д-К получилось что всё-таки чуть-чуть выше оценивают себя в среднем профи, не более.
В последней диаграмме, когда точки сливаются, вообще ничего сказать нельзя - мы не видим плотности точек там, где они слиты.
Обожаю такие статьи. Профаны настолько устали, что они потратили пару недель на тему, но их не принимают в профи, хотя они бьют себя кулаком в грудь, что написали профанскую статью-разоблачение и теперь бьют себя в грудь обоими кулаками.

Vpan
26.11.2023 09:30+1Хорошая статья, спасибо. Я понял ее так: глупые люди себя переоценивают, умные люди себя недооценивают и это действительно так. Но это происходит не потому что они глупые и умные, а это чисто статистическое явление из-за того, что самооценка не зависит или очень слабо зависит от фактических результатов.

printercu
26.11.2023 09:30+1(y−x) ∼ x
Видите проблему? Мы сравниваем x с его отрицательной версией.Это утверждение неверно, от этого все выводы из статьи неверные. Оно было бы верным только при константном у. Если у ~ х^10, то и (y−x) будет ~ х^10 на определенных интервалах.
Иронично, что статья, нацеленная на опровержение эффект Даннинга-Крюгера, подкрепляет его

Batalmv
26.11.2023 09:30+1Перечитывал несколько раз и вроде дошло
Итак, нас (неявно) просят сравнить y – x с x :
(y−x) ∼ x
Видите проблему? Мы сравниваем x с его отрицательной версией. Это автокорреляция по учебнику.
Мне кажется - ошибка здесь. Это ключевое место, где "найдена" автокоррекляция. На самом деле нет. Смотрите.
Есть Х - с ним все хорошо. Это объективные результаты тестов. Можно делить на группы и т.д.
Есть У - с ним тоже все хорошо. Это то, как свои способности оценивали люди. Тоже все ОК - реально объективная величина, которую померяли независимо.
Х и У - независимые величины. Ну как минимум если нет эффекта Даннига Крюгера. Но оказывается, что это нет так, значит есть возможность предположить, что какая-то связь есть. Главное ведь еще помнить, статистика не может говорить о том, что есть причинно-следственная связь, она может только сказать, что данные эксперимента ее не опровергают :)
Значения (Y-X) - я не понял, почему вас смушает, что там есть Х. Ну есть он там и что? В реальности это просто график для наглядности и не более того. Никакие доп. значения никак не повлияют на исходные Х и У.
Хотите считать, ну так берите исходные данные эксперимента и по классике: нулевая гипотеза и погнали. Excel за секунды все нарисует и покажет. И про р, и про автокорреляцию и еще кучу всего. Зачем так много писать? Данные, скрин полученного результата и все станет понятно.
Предположим, мы психологи, получившие крупный грант на повторение эксперимента Даннинга-Крюгера. Мы набираем 1000 человек, тестируем каждого из них и просим их пройти самооценку. Когда результаты будут получены, мы посмотрим на данные.
Вот это место я вообще не понял. Так эксперимент делался, либо картинку далее высосали из пальца и далее над результатами совершили набор "умозаключений"?

Rebelqwe
26.11.2023 09:30+1В попытках перехитрить нас, перехитрили сами себя. На рисунке 9 прекрасно видно, что эффекта никакого нет, данные по оценке не коррелируют с результатами теста. Из графика видно, что хорошо ставшие тест, так и плохо сдавшие тест одинаково некорректно оценивают свои способности (что и подтверждается в дальнейшем, ведь данные случайные). Надпись под рисунком утверждает, что есть большой эффект. Кого вы пытались надуть неверно интерпретировав график и построив на этом опровержение? То, что в реальности график Даннинга-Крюгера отличается от случайного и доказывает наличие эффекта.

Kergan88
26.11.2023 09:30+1На рисунке 9 прекрасно видно, что эффекта никакого нет, данные по оценке не коррелируют с результатами теста.
Так в этом эффект и состоит. Они должны коррелировать - а не коррелируют.
Из графика видно, что хорошо ставшие тест, так и плохо сдавшие тест одинаково некорректно оценивают свои способности
Что и является эффектом Даннинга-Крюгера, все верно.

ship2k
26.11.2023 09:30+2За это исследование авторам статьи была присуждена Шнобелевская премия по психологии за 2000 год (с) wiki

haldagan
26.11.2023 09:30+1В общем почитал немношк папир и комментарии на хакерранке и если отбросить громкие заявления, то по сути исследование 4 показывает, что если неподготовленному человеку дать почитать материалы по теме, то он внезапно показывает статистически значимое повышение в точности оценки своих предыдущих успехов в тесте, (что в общем-то интуитивно понятно).
По человекам:
Опрашивали студентов с одного курса Корнэльского университета. Минимальный проходной средний балл по предметам (GPA) 3.8 из 4 в 2023 и + "аналитический склад ума".
У меня есть подозрение, что при оценке своих способностей на фоне способностей товарищей они могут быть по умолчанию предвзяты, т.к. они всю жизнь были как минимум "значительно выше среднего" своих одноклассников по всем предметам и имели этому подтверждение в виде оценок.
Существуют ли подобные исследования, опрашивающие людей со средним/среднеспециальным образованием или что-то вроде того?
В смысле среди людей, предположительно не имеющих причин для предвзятости в оценке своих когнитивных способностей (в виде грамот, участия в олимпиадах, поступления в университет и т.п.)По оценкам:
Вопрос "как вы оцениваете свои успехи по сравнению с другими людьми с вашего курса" звучит странно. Мне (с моей дилетантской колокольни) кажется, что корректнее было бы спрашивать про "как вы оцениваете свои успехи в тесте" в баллах или процентах выполненных заданий и смотреть на точность оценки. ИМХО в формулировке вопроса про сравнение себя с другими может примешиваться целая куча искажений, т.е. эксперимент не чист.
P.S.: У меня почему-то есть ощущение, что если провести этот же самый тест среди (условно) шахтеров (тест со сложными логическими задачами), то они все поголовно причислят себя к нижнему/нижне-среднему квартилю.

Kergan88
26.11.2023 09:30P.S.: У меня почему-то есть ощущение, что если провести этот же самый тест среди (условно) шахтеров (тест со сложными логическими задачами), то они все поголовно причислят себя к нижнему/нижне-среднему квартилю.
Вы не учитываете что самооценка должна происходить ДО прохождение теста. Т.е. у шахтеров надо будет спросить: "как вы оцениваете свои логические способности, по шкале от 1 до 10?", а потом уже провести тест.

haldagan
26.11.2023 09:30После. Все оценки в бумаге происходят после прохождения теста без дополнительной информации.
В исследовании 3 происходит дополнительный раунд оценки после того, как участников также ознакомят с ответами некоторых из их сокурсников.
В исследовании 4 перед ознакомлением и повторной оценкой половину группы также заставляют прочитать учебник по логике.Upon arriving at the laboratory, participants were told that the study focused on logical reason-ing skills. Participants then completed a 20-item logical reasoning test that we created using questions taken from a Law School Admissions Test (LSAT) test preparation guide (Orton, 1993). Afterward, participants made three estimates about their ability and test performance.
Также стоит отметить, что в третьем исследовании были вопросы про грамматику, а в четвертом - снова про логику, но другие.

Kergan88
26.11.2023 09:30После.
Именно до, иначе результат будет существенно искажен. Если в описываемых экспериментах оно проводилось после - то там мусор а не данные, и смысла их обсуждать вообще нет. Можно с тем же успехом провести тест, назвать оценку за него а потом спросить эту оценку.

haldagan
26.11.2023 09:30Именно до
Я не совсем понял, с чем вы спорите. Я вам привел прямую цитату из оригинальной научной работы, в которой прямым текстом написано, что просили оценить уже после прохождения.
Я не предлагаю улучшить эксперимент, я предлагаю провести этот же самый эксперимент, но на людях, которые скорее всего сложных задач по формальной логике никогда в жизни не решали и, вероятно, должны знать о том, что скорее всего справились плохо.


no404error
Нет, наоборот. Знание без сомнений это не наука.
А эти ваши "чмошники" отрицают, не опровергая и не доказывая это, двухсотлентие определения молекулярной теории. Они буквально насрали на распределение Гаусса-Лапласа. Хотя оно имеет практическое применение в объективной реальности.
Даже опираясь на часть реальной науки, результат нерепрезентативен, в отличии от канона, имеющего приложение во множестве сред.