Sparkling: Открытая библиотека для автоматического решения задачи кластеризации табличных и мультимодальных данных / forpes.ru

Главная
Sparkling: Открытая библиотека для автоматического решения задачи кластеризации табличных и мультимодальных данных

Sparkling: Открытая библиотека для автоматического решения задачи кластеризации табличных и мультимодальных данных

23.12.2023 15:47

itmo_mllab 0 6600 Источник

Описание задачи

Задача кластеризации является востребованной и применимой в большом количестве разных сфер. Например, в медицине она может быть использована для выявления подгрупп пациентов со схожими характеристиками и симптомами для более точного лечения, в маркетинге для сегментирования целевой аудитории.

Неформально кластеризацию можно определить как разбиение множества объектов так, чтобы похожие объекты попали в одно и то же подмножество, а объекты из разных подмножеств существенно различались.

От обычной классификации по заданным признакам кластерный анализ отличается тем, что не человек, а алгоритм выявляет критерий кластеризации данных. Эта задача относится к классу «обучения без учителя» (англ. unsupervised learning), так как размеченного набора данных или какой-то заведомо известной информации о нём не предоставляется.

*Источник изображения: commons.wikimedia.org.*

У задачи кластеризации нет общепризнанного математически корректного определения, ввиду отсутствия формализации меры близости между объектами.

Универсальный алгоритм, который подходит для всех задач, построить невозможно (теорема Клейнберга). Принципиально невозможно найти решения задачи кластеризации, ведь существует множество критериев оценки качества разбиения, а число кластеров обычно неизвестно заранее. Поэтому алгоритмы кластеризации нужно подбирать и настраивать почти для каждой задачи отдельно.

Задача выбора и настройки алгоритма машинного обучения является экспертной, что достаточно затратно по времени, поскольку работа выполняется человеком фактически вручную. Автоматизация подбора и настройки алгоритмов кластеризации экономит множество интеллектуальных, временных и других ресурсов в разных областях применения кластерного анализа. Система, которая могла бы автоматически рекомендовать и настраивать подходящий алгоритм кластеризации для каждой задачи в отдельности, была бы весьма актуальна.

Почему важно уметь настраивать алгоритмы?

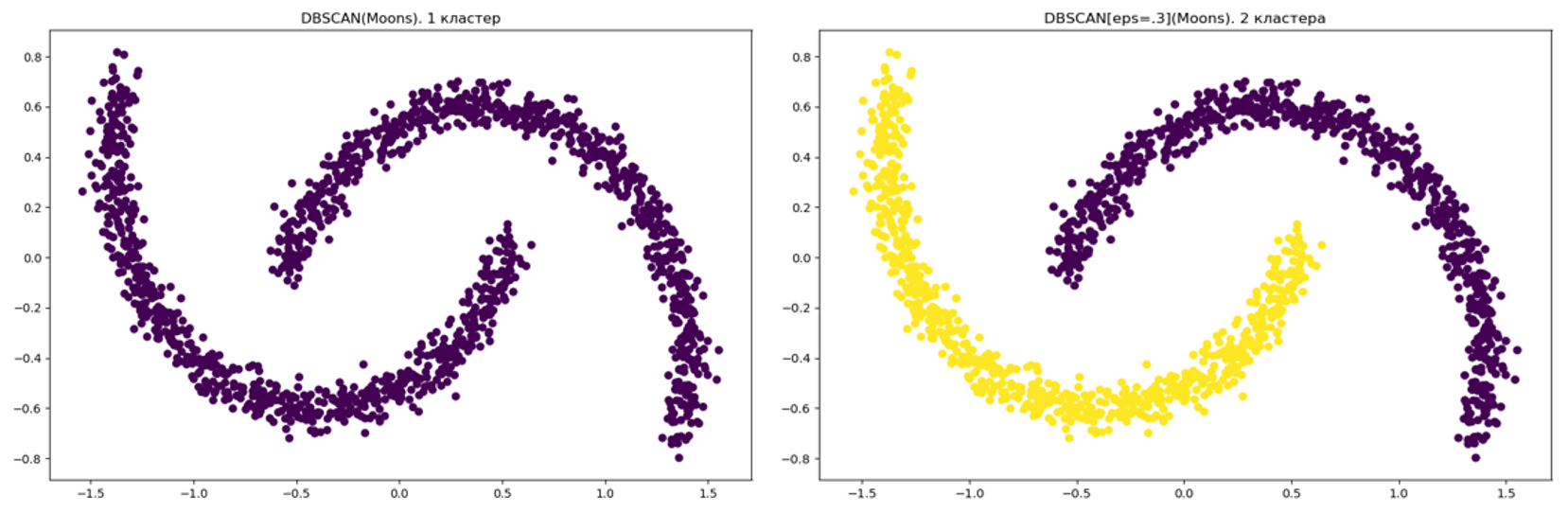
Выбор гиперпараметров может существенно повлиять на качество работы, классический пример работы алгоритма DBSCAN c разным набором гиперпараметров.

Сравнение применения алгоритмов с параметрами по умолчанию и с настроенными гиперпараметрами.

Существующие решения

Говоря о существующих решениях, подавляющее большинство библиотек применимо ислючительно в supervised домене. Для задачи кластеризации существует лишь одно кустарное решение (autocluster), которое работает лишь с базовыми реализациями из sklearn и не поддерживает работу с большим объёмом данных и мультимодальность, .

Таким образом, для задач кластеризации не найдено инструмента для автоматической настройки и выбора соответствующего задаче алгоритма, который поддерживал бы мультимодальность и работу с большими наборами данных.

Для решения этой проблемы можно выделить две задачи:

Распределённый алгоритм рекомендация меры качества разбиения
Выбор и настройка алгоритма кластеризации мультимодальных больших данных по заданной мере

Как оценивать разбиения?

Ключевая сложность, с которой пришлось столкнуться в процессе исследования, состояла в том, чтобы понять, как корректно подобрать меру качества, по которому сравниваются возможные решения. Эту сложность получилось преодолеть с помощью рекомендации меры качества разбиения для каждой задачи на основе принципа мета-обучения.

Основная идея мета-обучения состоит в сведении задачи выбора алгоритма к задаче обучения с учителем: задачи описываются мета-признаками, характеризующими свойства решаемой задачи, при этом агрегированные сведения о работе алгоритмов (лучший алгоритм, ранжирование над алгоритмами и т.д.) выступают целевой функцией в такой постановке. Это может быть как сам алгоритм, так и оценка его работы на конкретной задаче по какой-либо мере.

Таким образом удалось разработать методологию визуальной оценки мер на основе визуальной оценки разбиений и сведении задачи предсказания такой оценки для новых наборов данных к задаче классификации в пространстве мета-признаков, описывающих поставленную задачу кластеризации. Далее расскажем об этом подробнее.

Сравниваем разбиения

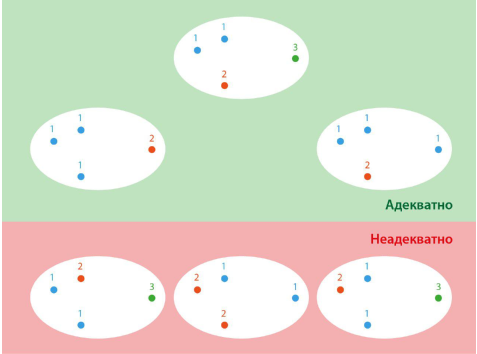
Берём алгоритмы кластеризации и применяем их к набору данных. Полученные разбиения можно оценивать как адекватные или неадекватные, а ещё можно проводить сравнения разбиений друг с другом, чтобы определить лучшие. На рисунке ниже приведён пример сравнения различных разбиений примитивного набора данных с точки зрения адекватности, а также с точки зрения сравнения разбиений друг с другом. Чем выше на рисунке расположено разбиение, тем оно лучше с точки зрения попарного сравнения с другими разбиениями.

Сравниваем меры качества

Основываясь на критериях оценки качества кластеризации с точки зрения визуального восприятия, я ввёл два критерия мер качества — критерий адекватности и критерий ранжирования.

Критерий адекватности меры — оценка адекватности лучшего разбиения заданного набора данных с точки зрения визуального восприятия.

Критерий ранжирования — нормированная функция расстояния между ранжированием разбиений, задаваемым мерой качества, и агрегированным ранжированием разбиений, задаваемым оценками на основе визуального восприятия. Область значения данной функции: чем значение функции ближе к тем рассматриваемая мера качества лучше.

Для наглядности давайте рассмотрим пример с набором данных набора данных 2D-200. Для каждого набора данных из 2D-200 мы сформировали 14 разбиений. Эти разбиения были оценены пятью асессорами и девятнадцатью мерами качества. В итоге на наборе данных 2D-200 выявлены лучшие меры качества с точки зрения критериев и Затем для каждой меры по всем элементам из 2D-200 были вычислены следующие величины:

$BestCVI_{Adq}$ — соотношение числа раз, когда мера отвечала критерию адекватности к общему числу экспериментов;

$BestCVI_{R}$ — соотношение числа раз, когда мера была лучшей с точки зрения критерия ранжирования к общему числу экспериментов.

Значения $BestCVI_{Adq}$ и $BestCVI_{R}$ для всех мер качества на наборе данных наборов данных 2D-200 представлены в таблице ниже.

Мера	$BestCVI_{Adq}$	$BestCVI_{R}$	Мера	$BestCVI_{Adq}$	$BestCVI_{R}$
DB			Sym
Dunn			CI
Sil			DB*
CH			gD31
S_Dbw			gD41
SymDB			gD51
CS			gD33
COP			gD43
SF			gD53
OS

Из таблицы видно, что ни одна рассмотренная мера не претендует на универсальность по введенным критериям, а значит, меру качества нужно рекомендовать для каждого набора данных отдельно.

Однако эффективная рекомендация из девятнадцати мер качества требует значительно большего числа наборов данных, чем представлено в 2D-200. Поэтому я построил множество из четырех самых лучших мер с точки зрения — среднего значения, вычисляемого на основе критерия ранжирования мер: мера Silhouette, мера Calinski-Harabasz, мера gD41 и мера SF. В таблице приведены значения для всех мер.

Мера	$AvgCVI_{R}$	Мера	$AvgCVI_{R}$
*gD41*	$\mathbf{0{,}369}$	gD53
gD43		S_Dbw
gD33		Dunn
OS		gD51
CH	$\mathbf{0{,}369}$	CI
*Sil*	$\mathbf{0{,}370}$	CS	$\mathbf{0{,}370}$
SF	$\mathbf{0{,}370}$	DB
Sym		COP
gD31		DB*
SymDB

Классификатор, который рекомендует меру качества

Всякий раз производить данные вычисления довольно ресурсозатратно. Можно упростить задачу рекомендации меры качества, если свести её к задаче классификации. И я решил построить классификатор, который для нового набора данных предсказывает, какая из рассматриваемых мер качества будет лучше с точки зрения агрегированных оценок асессоров, если бы они действительно проходили описанный выше тест для этого набора данных. В качестве классификатора мы использовали алгоритм XGBoost, который выбрал экспериментально и который показывает качество классификации Интересно, что разработанный мета-классификатор сам по себе выступает новой мерой качества, назовём её Meta-CVI.

Выбор и настройка алгоритмов кластеризации

Проблема в том, что заранее невозможно предсказать, насколько качественное разбиение построит тот или иной алгоритм. Если уделять равное время настройке всех возможных для данной задачи алгоритмов, то получится, что большая часть времени при такой схеме будет потрачена на настройку заведомо неэффективных алгоритмов. Но если сосредоточиться лишь на одном алгоритме, то часть из тех, что могли бы обеспечить лучшее качество кластеризации, не будут рассматриваться.

Чтобы решить эту проблему, мы разработали метод выбора и настройки алгоритмов на базе обучения с подкреплением. Этот метод сводится к задаче о многоруком бандите. Алгоритм осуществляет поиск компромисса между исследованием и эксплуатацией процессов настройки параметров для различных алгоритмов кластеризации.

В задаче о многоруком бандите рассматривается агент, тянущий за ручки тотализатора, с каждой из которых связано некоторое неизвестное распределение награды. Каждый ход агент выбирает ручку и получает случайную награду из связанного с ней распределения. Цель агента — максимизировать полученную за несколько итераций награду.

Давайте формализуем задачу. Пусть задан некоторый временной бюджет на поиск лучшего алгоритма Требуется разбить его на интервалы таким образом, что при запуске процессов $\pi_j$ с ограничением по времени получается значение меры качества такое, что:

$Q(A_{\lambda_j}^{j}) \xrightarrow{(t_1, t_2, \ldots, t_m)} \min_j,$

где $A^j \in A, \lambda = \pi(t_i, A^j, \emptyset),$ и $t_1 + \ldots + t_m = T, t_i \geq 0 \: \forall i.$

В этом случае каждой ручке алгоритма многорукого бандита соответствует определённая модель алгоритма кластеризации из конечного множества вызову ручки на итерации — процесс оптимизации гиперпараметров этой модели в течение времени В результате будет достигнуто качество кластеризации $Q(A_{\lambda_i}^{i}, D).$

Качество кластеризации определяется с помощью меры, получаемую по завершении итерации, которая является ключевым параметров в функции награды. Награда представляет собой функцию от меры качества и времени

Выбор следующей ручки для запуска определялся с помощью классических алгоритмов решения задачи о многоруком бандите – Softmax и UCB.

На изображении ниже приведён процесс работы настройщика: на вход подаётся уже предобработанный набор данных SparklingDF, мера и временной бюджет, цикл после вычисления награды выполняется до тех пор, пока не закончится временной бюджет.

Иллюстрация работы конечного метода выбора и настройки алгоритма кластеризации представлена на рисунке ниже:

Мультимодальность и большие данные

Библиотека Sparkling поддерживает работу с мультимодальными данными: табличные, графические данные и текстовые и табличные, различные комбинации модальностей.

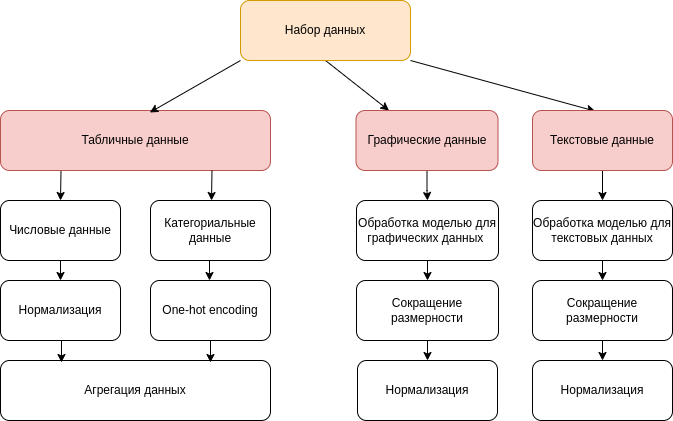
Как работать с мультимодальными данными?

После предварительного анализа мы приняли решение разработать собственный способ подсчёта расстояния в мультимодальном пространстве по исходя из следующих причин:

При каждом новом наборе данных переобучать модель глубокого обучения вычислительно дорого.
Функция подсчета расстояний при решении задач кластеризации вызывается много раз, в связи с этим она не должна быть вычислительно слишком затратной.
На распределенную реализацию таких глубоких нейронных сетей уйдёт слишком много времени

Последний пункт важен особенно, поскольку в зависимости от задачи для разных данных могут использоваться разные метрики расстояния, например, евклидово расстояние или косинусная мера на практике не всегда применимы.

Для подсчёта расстояний в библиотеке используется следующая эвристика:

Пусть – количество модальностей, $\alpha_1...\alpha_N$ – некоторые нормировочные коэффициенты, а – расстояния между модальностями (векторными представлениями) объектови Тогда расстояниемежду объектамии вычисляется как:

$L= \sqrt (\alpha_1 l_1^2+\alpha_2 l_2^2+⋯+\alpha_N l_N^2)$

Другими словами, расстояние между объектами с разными модальностями рассчитывается как норма радиус-вектора, у которого координаты – это расстояния между соответственными модальностями объекта (текст, табличные данные или изображения) с коэффициентами, нормированными в зависимости от размера векторного представления.

Как получаем эмбеддинги?

В библиотеке реализована поддержка двух фреймворков: Pytorch и Tensorflow. Препроцессинг графических и текстовых данных осуществляется при помощи моделей платформы HuggingFace. При выборе соответствующей модели, она загружается в проект по ссылке и в дальнейшем используется.

Как это работает с большими данными?

Учитывая, что мы хотим реализовать работу с большими данными, а также что метрика подсчёта расстояния имеет свою специфику с учётом предложенного выше подхода, потребовалось заново реализовать алгоритмы кластеризации и меры оценки качества разбиений в парадигме MapReduce. Были реализованы следующие алгоритмы кластеризации:

K-Means
MeanShift
Спектральный алгоритм
BIRCH
Bisecting K-Means

Также были реализованы внутренние меры качества:

Silhouette
Calinski-Harabasz
Generalized Dunn (gD41, см. выше)
Score Function (SF)

и внешние меры качества, если в наборе данных присутствует разметка и пользователь пожелает оценить разбиение с этой точки зрения:

Jaccard index
Rand index
F-мера для кластеризации

Модули библиотеки

В библиотеке можно выделить два основных модуля: Sparkling и Heaven. В первых версиях вся реализация была на PySpark, однако в ходе экспериментов было выявлено, что Все "тяжеловесные" реализации вынесены в модуль Heaven, который написан на Scala, что позволяет оптимизировать выполнение кода.

Sparkling	Heaven
Язык: Python.	Язык: Scala
Функционал: Препроцессинг, подключение эмбеддингов, процесс оптимизации и взаимодействие с пользователем.	Функционал: Мультимодальная мера, реализации алгоритмов кластеризации и мер качества.
Зависимости: необходимы сторонние модули python в зависимости от конкретной задачи.	Зависимости: Не требуют дополнительных зависимостей, помимо Apache Spark.

Взаимодействие с библиотекой

Краткие минимальные требования:

Ubuntu 16.04, 20.04, 22.04;
JDK 8
Conda
Pyspark 2.4.6
Развернуть кластер под YARN, если у вас есть сервер на несколько машин.

Процесс установки, спецификация и возможные проблемы подробно приведены тут.

После установки нужно инициализировать Spark сессию, обязательно указав путь до heaven.jar:

import pyspark

from sparkling import *

conf = pyspark.SparkConf() \        
  .setAppName('sparkling-unimodal') \        
  .setMaster('local-cluster[4, 2, 1024]') \    
  .set('spark.default.parallelism', '4') \      
  .set('spark.jars', 'bin/heaven.jar')

sc = pyspark.SparkContext.getOrCreate(conf)

Для функционирования библиотеки также необходимо указать checkpoint директорию:

sc.setCheckpointDir('examples/checkpoint')

После того, как прочитали датасет, отправим его в препроцессинг. Обозначим наличие внешних меток в колонке class, а все остальные колонки соотнесем с единственной табличной модальностью:

sql = pyspark.SQLContext(sc)

df = sql.read.csv(f'{DATA_ROOT}/{DATASET}.csv', inferSchema=True, header=True)

feature_cols = set(df.columns) - {'class'}

builder = SparklingBuilder(df, class_col='class', partitions='default') \        
  .tabular('features', feature_cols, Distance.EUCLIDEAN)

sparkling_df = builder.create()

После прохождения всех этапов предобработки возвращается SparklingDF - обертка над pyspark.sql.Dataframe с дополнительной мета-информацией для внутренних нужд. Можно легко получить доступ к нативному датафрейму (но любое его изменение может приведести к UB):

sparkling_df.df.show()

+------+----+--------------------+
|_class| _id|            features|
+------+----+--------------------+
|     3|3883|[-0.5098039215686...|
|     3| 881|[-0.4509803921568...|
|     2|2709|[-0.6666666666666...|
|     3|4461|[-0.6078431372549...|
|     3|1368|[-0.7254901960784...|
|     3|2599|[-0.5294117647058...|
|     3|4582|[-0.4313725490196...|
|     3|2277|[-0.8823529411764...|
|     2|1418|[-0.4705882352941...|
|     3|4715|[-0.8627450980392...|
|     3|1600|[-0.5882352941176...|
|     3|1548|[-0.4509803921568...|
|     3|3122|[-0.8039215686274...|
|     4| 968|[-1.0,-0.48076923...|
|     3|2003|[-0.5686274509803...|
|     3|2949|[-0.6078431372549...|
|     3|3146|[-0.7058823529411...|
|     3|1663|[-0.5098039215686...|
|     3|4143|[-0.6666666666666...|
|     2|3296|[-0.6078431372549...|
+------+----+--------------------+

Теперь создаем оптимизатор и запускаем его на 100 секунд. Для указания таргет меры используем параметр measure:

optimiser = Sparkling(sparkling_df, measure=Internal.CALINSKI_HARABASZ)

optimal = optimiser.run(time_limit=100)

Возвращаемый объект Optimal представляет размеченный датафрейм (колонка _label со значениями от 0 до k - 1, k - количество кластеров), который является наилучшим с точки зрения таргет меры. В нем же содержатся значение таргет меры, алгоритм с гиперпараметрами и обученная модель кластеризации.

print(f'{optimiser.measure.name}: {optimal.value}')

optimal.label_sdf.df.show()

+------+----+--------------------+------+
|_class| _id|            features|_label| 
+------+----+--------------------+------+ 
|     3|3883|[-0.5098039215686...|     1| 
|     3| 881|[-0.4509803921568...|     0| 
|     2|2709|[-0.6666666666666...|     0| 
|     3|4461|[-0.6078431372549...|     1| 
|     3|1368|[-0.7254901960784...|     0| 
|     3|2599|[-0.5294117647058...|     0| 
|     3|4582|[-0.4313725490196...|     0| 
|     3|2277|[-0.8823529411764...|     1| 
|     2|1418|[-0.4705882352941...|     0| 
|     3|4715|[-0.8627450980392...|     0| 
|     3|1600|[-0.5882352941176...|     0| 
|     3|1548|[-0.4509803921568...|     1| 
|     3|3122|[-0.8039215686274...|     1| 
|     4| 968|[-1.0,-0.48076923...|     1| 
|     3|2003|[-0.5686274509803...|     1| 
|     3|2949|[-0.6078431372549...|     0| 
|     3|3146|[-0.7058823529411...|     0| 
|     3|1663|[-0.5098039215686...|     0| 
|     3|4143|[-0.6666666666666...|     1| 
|     2|3296|[-0.6078431372549...|     0| 
+------+----+--------------------+------+ 
only showing top 20 rows

Поскольку теперь у датафрейма появилась разметка, можно оценить ее другими мерами качества (в том числе и внешними, поскольку у исходного датасета присутствовали внешние метки):

print(f'F1: {External.F1.evaluate(optimal.label_sdf)}')

print(f'RAND: {External.RAND.evaluate(optimal.label_sdf)}')

print(f'SILHOUETTE: {Internal.SILHOUETTE.evaluate(optimal.label_sdf)}')

print(f'GD41: {Internal.GD41.evaluate(optimal.label_sdf)}')

Если есть необходимость, можно дампнуть историю оптимизации - какие конфигурации алгоритмов кластеризации были сэмплированы, сколько было потрачено времени на обучение модели и оценку разметки, а также сами значения таргет меры:

with open(f'examples/logs/{DATASET}.json', 'w') as fp:       
  fp.write(optimiser.history_json())

Пробуем мультимодальный датасет

Для обработки мульмимодальных данных нужно при инициализации сессии активировать pyarrow:

import pyspark

from pyspark.sql import functions as F
from pyspark.sql.types import IntegerType 
from sparkling import *
from sparkling.emb.torch import TorchTexts

conf = pyspark.SparkConf()\        
  .setAppName('sparkling_pytorch_text')\        
  .setMaster('local-cluster[2, 1, 4096]')\     
  .set('spark.sql.execution.arrow.enabled', 'true')\    
  .setExecutorEnv('ARROW_PRE_0_15_IPC_FORMAT', '1')\    
  .set('spark.jars', 'bin/heaven.jar')

ss = pyspark.sql.SparkSession.Builder().config(conf=conf).getOrCreate()

ss.sparkContext.setCheckpointDir('examples/checkpoint')

Далее достаточно "уведомить" SparklingBuilder о наличии других модальностей:

df = ss.read.csv('examples/data/popular-quotes/raw.csv', inferSchema=True, header=True)\
  .withColumn('Likes', F.col('Likes').cast(IntegerType()))\    
  .withColumn('quotes', F.trim(F.col('Popular Quotes')))\    
  .withColumn('Author Names', F.trim(F.col('Author Names')))

builder = SparklingBuilder(df, partitions='default')\    
  .tabular('popularity', {'Author Names', 'Likes'})\    
  .text('quotes', TorchTexts.MOBILE)

sparkling_df = builder.create()

Здесь мы неизбежно сталкиваемся с выбором NLP модели, которая будет трансформировать текстовые данные в векторное представление. На текущий момент список поддерживаемых моделей прибит гвоздями, в дальнейшем планируется позволить пользователю скормить любую модель из transformers. Обратите внимание, что модель копируется на все узлы кластера, поэтому учитывайте доступные Вам ресурсы при выборе.

В остальном код не меняется - создали и запустили оптимизатор, при желании - дампнули историю:

optimiser = Sparkling(sparkling_df, measure=Internal.SILHOUETTE_APPROX)

print(optimiser.run(time_limit=80))

with open(f'examples/logs/popular-quotes-local.json', 'w') as fp:    
  fp.write(optimiser.history_json())

А как дела с изображениями?

Обработка датасета с изображениями практически не отличается от текстового. По аналогии, нужно активировать pyarrow и указать в SparklingBuilder модальность типа image:

builder = SparklingBuilder(df, class_col='class', partitions='default')\    
  .image('celebrity', TorchImages.SWIN_TRANSFORMER, str(root), Distance.MANHATTAN)

Список доступных моделей также ограничен. Заметим, что в соответствующей колонке ожидается путь до файла с изображением, притом root + <path> должен быть абсолютным. Sparkling вычитывает изображения из файловой системы (будь то локальная ext4 или hdfs на кластере) небольшими батчами и скармливает их в модель для получения эмбеддингов.

Далее код будет точно таким же, как в предыдущих примерах, не будем дублировать.

Настройка оптимизатора

До этого момента мы при создании оптимизатора указывали только таргет меру, однако можно более гибко приспособить его для Ваших нужд и окружения.

mab_solver – стратегия многорукого бандита, доступны SOFTMAX и UCB;

hyper_opt – используемая под катом библиотека для байесовской оптимизации (OPTUNA или SMAC);

configs – можно задать используемые алгоритмы кластеризации и их пространство поиска. По умолчанию используются все реализованные алгоритмы с эвристически заданными наборами гиперпараметров;

measure - можно указать одну из доступных внутренних мер, либо указать None. В этом случае будет рекомендована одна из четырех мер на основе мета-обучения.

Пример работы с мультимодальным набором данных

P.S. будем рады новым контрибьюторам: https://gitlab.com/rainifmo/sparkling/-/tree/master