
Хабр, привет! Меня зовут Антон Разжигаев, я аспирант Сколтеха и участник научной группы Fusion Brain в институте AIRI.
С момента выхода первой статьи «Attention is All You Need» я с жадностью и любопытством, присущими любому исследователю, пытаюсь углубиться во все особенности и свойства моделей на базе архитектуры трансформер. Но, если честно, я до сих пор не понимаю, как они работают и почему так хорошо обучаются. Очень хочу разобраться, в чём же причина такой эффективности этих моделей, и есть ли предел их возможностей?
Такому изучению трансформеров «под микроскопом» и посвящена наша научная работа, только что представленная на конференции EACL 2024, которая проходила на Мальте — «The Shape of Learning: Anisotropy and Intrinsic Dimensions in Transformer-Based Models». В этой работе мы сфокусировались на наблюдении за пространством эмбеддингов (активаций) на промежуточных слоях по мере обучения больших и маленьких языковых моделей (LM) и получили очень интересные результаты.
Итак, приступим!
Данные
Начнём с рассказа о данных — это нужно для того, чтобы было проще понять, что мы сделали и что обнаружили. Т.к. нас интересовало пространство контекстуализированных эмбеддингов (в т.ч. промежуточных), надо было их где-то добыть.
Мы взяли enwik8 — аккуратно очищенные статьи Википедии на английском языке. Эти тексты мы прогнали через изучаемые модели, сохраняя все промежуточные активации (для каждого токена и с каждого слоя). Так мы получили «пространство эмбеддингов» или, другими словами, многомерное облако точек, с которым и стали дальше работать.
Чтобы исключить зависимость наблюдений от выбранного датасета, мы повторили эксперименты на случайных последовательностях токенов, и все выводы повторились. Поэтому в дальнейшем не буду акцентировать на этом внимание, а лучше сразу перейду к результатам.
Анизотропия
Один из самых главных вопросов, которые мы себе задали в процессе исследования — а какая вообще форма у этих облаков точек? Визуализировать их сложно — пространство эмбеддингов очень многомерно, — а методы снижения размерности тут не сильно помогают. Поэтому мы решили использовать анизотропию в качестве нашего «микроскопа». Анизотропия — это мера, показывающая насколько облако точек вытянуто, насколько оно неоднородно. Чем выше это значение, тем сильнее вытягивается пространство.

К примеру, уже давно известно (см. статью Representation Degeneration Problem in Training Natural Language Generation Models), что эмбеддинги трансформеров-энкодеров лежат в «узком конусе» — из-за этого косинусы между текстовыми репрезентациями всегда очень высокие. Но тем не менее, если вычесть среднее значение и отцентрировать это облако точек, оно становится вполне изотропным, то есть похожим на многомерный шарик. Поэтому говорят, что эмбеддинги трансформеров-энкодеров (Bert, RoBERTa, Albert, …) локально изотропны.
А в случае с декодерами (GPT, Llama, Mistral, …) мы обнаружили, что это совершенно не так! Даже после центрирования и использования более устойчивых к смещению методов на базе сингулярных чисел мы видим, что на средних слоях языковых моделей анизотропия практически равна 1. Это означает, что облако точек там вытянуто вдоль прямой линии. Но почему? Это же так сильно снижает ёмкость модели, она из-за этого практически не использует ТЫСЯЧИ других размерностей.

Откуда берётся эта неоднородность пространства репрезентаций в декодерах, мы пока не знаем, но предполагаем, что это связано с процессом их обучения, задачей предсказания следующего токена и треугольной маской внимания. Это одна из исследовательских задач, которая сейчас стоит перед нами.
Если посмотреть на профиль анизотропии по слоям, то становится видно, что в начале и в конце декодеров эмбеддинги гораздо более изотропны, а экстремально высокая анизотропия наблюдается только в середине, где и должен происходить весь мыслительный процесс.
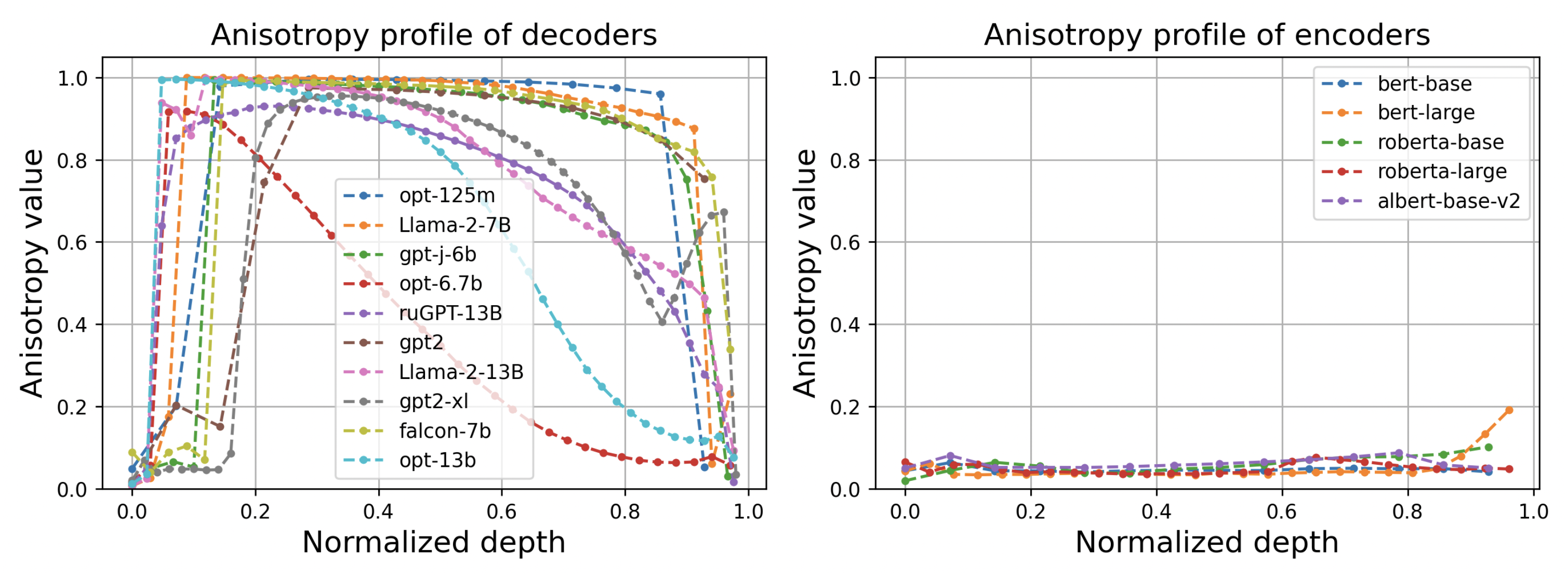
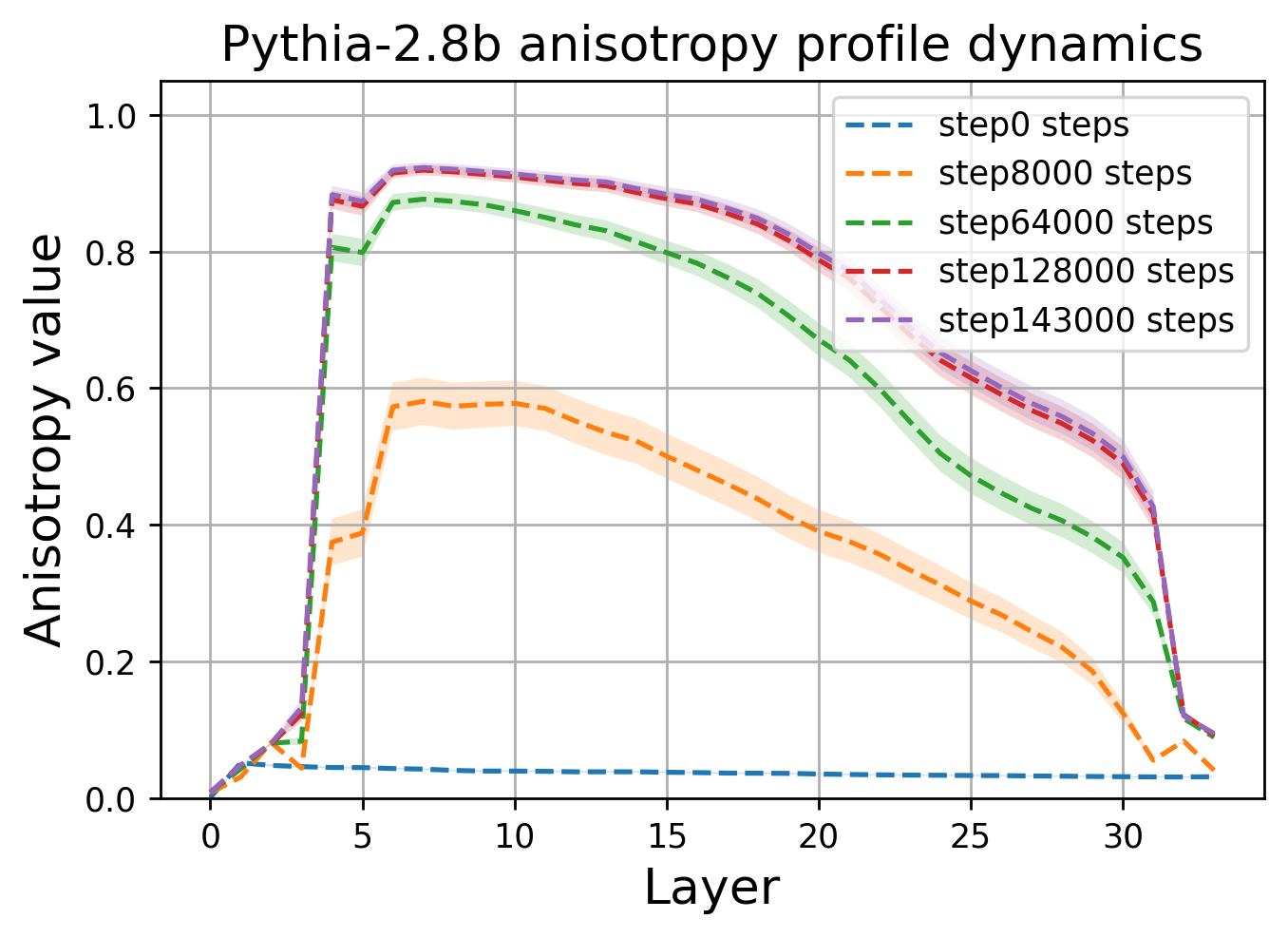
Мы проследили за тем, как меняется анизотропия от чекпоинта к чекпоинту по мере обучения моделей (мы взяли все модели с промежуточными весами из того, что было опубликовано на тот момент). Оказалось, что все модели класса трансформер-декодер постепенно сходятся к одной и той же форме пространства и одному и тому же куполообразному профилю анизотропии.
Внутренняя размерность
Следующий наш «микроскоп» для наблюдения за активациями — внутренняя размерность. Это довольно красивое математическое понятие, описывающее «сложность» фигуры (многообразия или манифолда), на котором располагаются точки в многомерном пространстве.
Чтобы было понятнее, рассмотрим трёхмерную фигуру в виде ленты, свёрнутой в спираль (см. картинку ниже). Если мы приблизимся к какому-либо её участку, то обнаружим, что в малой окрестности точки будто бы лежат на плоскости. Следовательно, локальная внутренняя размерность тут равна двум.
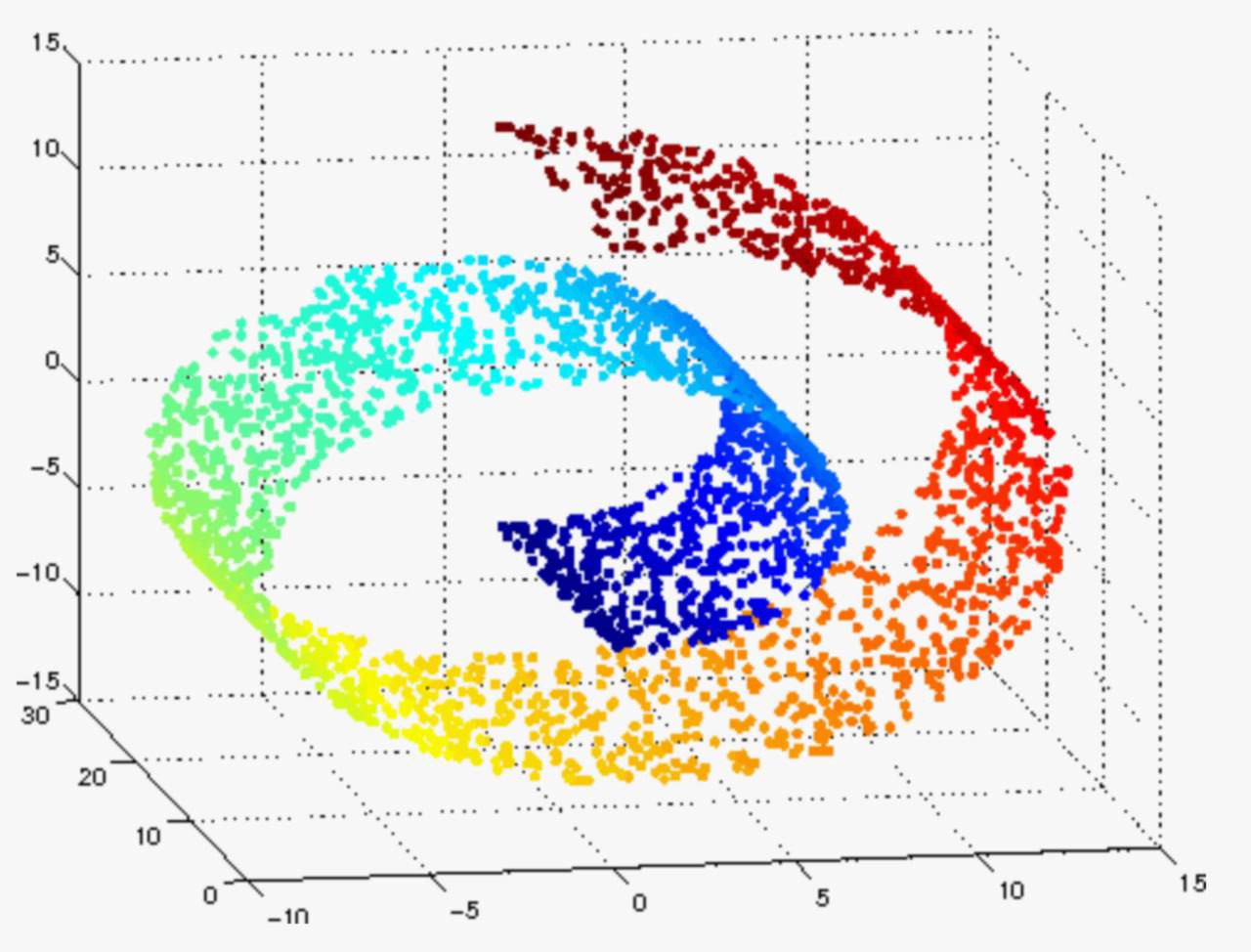
Самое главное, что внутреннюю размерность довольно легко оценить, так как она сильно связана со скоростью роста «объёма» многомерного шара (количества точек данных, попадающих внутрь шара) по мере увеличения радиуса. Измерение зависимости количества точек от радиуса позволяет определить внутреннюю размерность в локальной области облака данных.
Итак, что же мы обнаружили? Во-первых, размерность довольно низкая, но это не новость, т.к. это было обнаружено и до нас. Во-вторых, — и это гораздо интереснее — эта размерность изменяется одинаково для всех моделей по мере обучения! Этот процесс состоит из двух фаз — сначала рост, а затем падение (см. график).
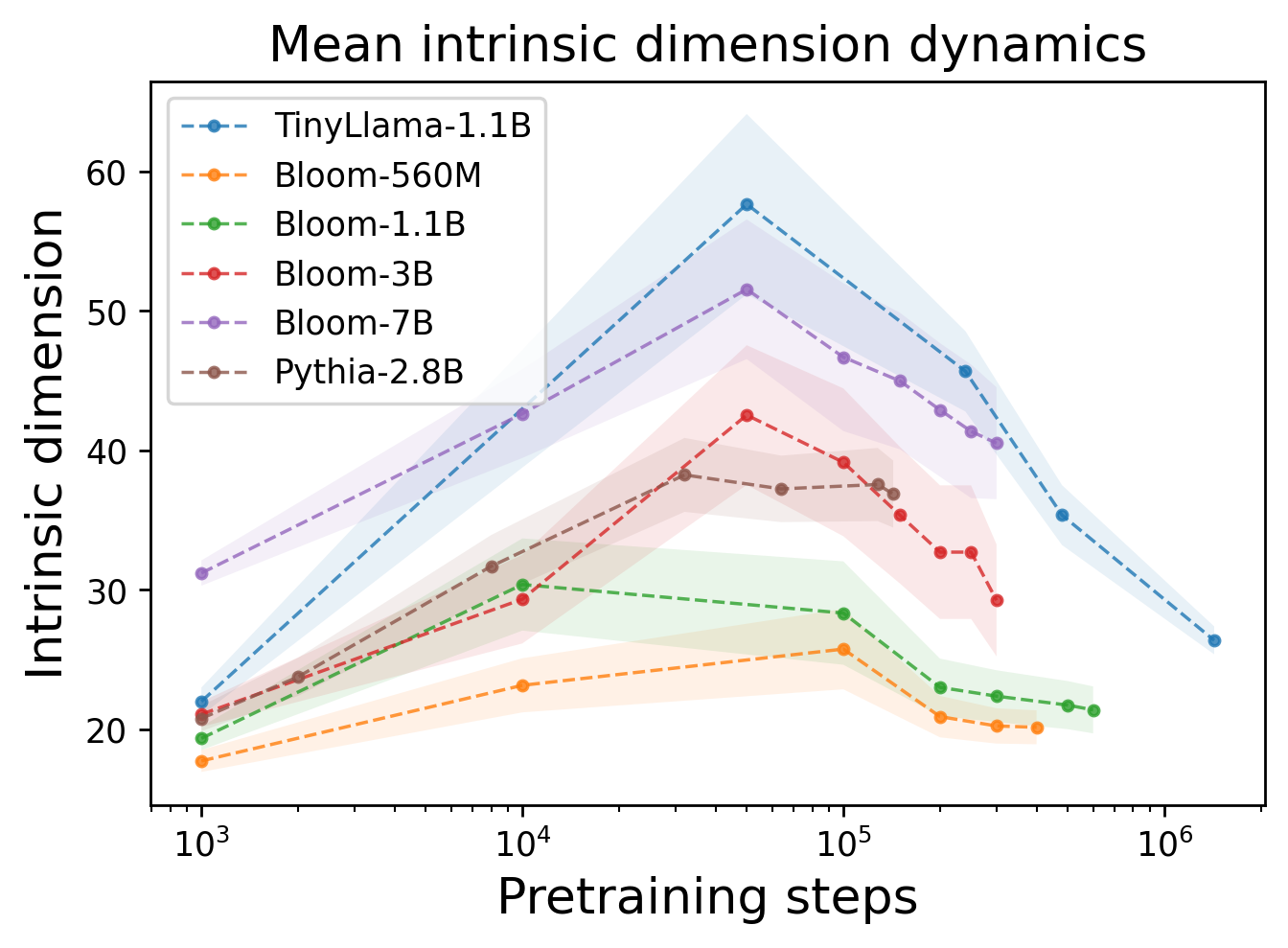
Похоже, что первая часть обучения переводит фичи в более высокие измерения, чтобы «запомнить» как можно больше информации, а во второй фазе — фичи начинают сжиматься, позволяя выявлять больше закономерностей, усиливая обобщающие способности модели.
Ещё раз — у всех LLM во время обучения присутствуют две фазы: инфляция эмбеддингов и их последующая компрессия.
Что это даёт?
Мы верим, что, вооружившись новым знанием, мы сможем улучшить процесс обучения языковых моделей (и не только), сделать его эффективнее, а сами трансформеры — быстрее и компактнее. Ведь если эмбеддинги проходят стадию компрессии и вообще стремятся расположиться вдоль одной линии, то почему бы просто не повыкидывать неиспользуемые измерения? Или помочь модели с более быстрым преодолением первой фазы.
Также мы обнаружили, что незадолго до взрывов лосса во время обучения (больная тема всех, кто учит LLM) внутренняя размерность сильно подрастает. Возможно, у нас получится предсказывать взрывы лосса и не тратить вычислительные ресурсы впустую, или вообще победить эти нестабильности, поняв их природу.
Хотя кого я обманываю, всё это нужно только ради удовлетворения своего любопытства!
Подписывайтесь на каналы авторов в телеграме AbstractDL, CompleteAI, Dendi Math&AI, Ivan Oseledets. В работе также принимали участие коллеги из AIRI, Сбера, Сколтеха, МГУ, ВШЭ и Самарского университета.
Комментарии (14)

kmmbvnr
01.04.2024 14:32А не было попытки узнать, есть ли смысл у осей многомерного пространства? Может если как-то повернуть, на всех осях окажутся определенные типы слов

Razant Автор
01.04.2024 14:32+4Да, были работы про "линейный пробинг" эмбеддингов, удалось выявить направления, связанные с координатами и временем (Language Models Represent Space and Time). Работает не идеально, но работает)

krisgrey
01.04.2024 14:32+1Получается, что современный подход к организации обучения позволяет моделям самопроизвольно находить оптимальную комбинацию мыслительных процессов - накопление знаний и их редукцию для формулирования выводов.
Напрашиваются закономерные вопросы:
1) можно ли использовать средний слой с максимальным объёмом знаний как репрезентацию внутреннего мира модели?
2) если учесть, что левая половина слоёв кодирует информацию, а правая - декодирует, то не присутствует ли некая параллель между соответствующими слоями, отстоящими от середины? Можно ли использовать эти параллели для оптимизации графа вычислений (можно ли провести какую-то нормализацию модели типа зеркалирования половин слоёв, но чтобы ответы были такими же, как у исходной)?
Было бы интересно в дальнейшем узнать, как влияют LoRa на поведение внутренних размерностей.
Razant Автор
01.04.2024 14:32+1Кстати, на задачах линейного пробинга действительно видно, что средние слои декодеров дают лучшую точность классификации. То есть если модель заморожена и можно обучать только логистическую регрессию поверх эмбеддингов, то лучше брать эмбеддинги из середины.
Вот такой у нас получился график для классификации CIFAR в другой статье про imageGPT.

phenik
01.04.2024 14:32+2Если посмотреть на профиль анизотропии по слоям, то становится видно, что в начале и в конце декодеров эмбеддинги гораздо более изотропны, а экстремально высокая анизотропия наблюдается только в середине, где и должен происходить весь мыслительный процесс.
Интересно наблюдать как исследователи свойств ИНС проходят в облегченной форме исследования которые проводили нейрофизиологи на биологических сетях) В облегченной потому как не нужно возится с подопытными и аппаратурой, типа фМРТ и др, а манипулировать только массивами чисел - весов. С другой стороны это полезно, как моделирование нейрофизиологии. В данном случае речь о компрессии информации в мозге. Разнообразных исследований на эту тему множество, они ведутся давно, с тех пор, как была установлена суммативная функция нейронов и сетей в целом, в частности, при сенсорном вводе. Сети, как правило, производят нелинейную фильтрацию информации. Лучшей моделью для сенсорных сетей являются глубокие сверточные с архитектурой подобной структуре вентрального тракта зрительной системы приматов. Но и ассоциативные области мозга, отвечающие за обработку языка, которые условно моделируются в ЯМ, также подчиняются похожим закономерностям. Генерализация - обобщение, в этом случае это абстрагирование, а абстракции связаны с компрессией.
Приведу пример исследования по временной суммации (компресси) в зрительной системе. Аналогичные закономерности наблюдаются и при пространственной суммации, и иллюстрируются такой схемой. Степень сжатия в последовательных отделах зрительного тракта, прототипах слоев в ИНС сверточного типа, изображена на рис. 3 C. Вполне напоминает приведенные в статье по анизотропии по слоям для ЯМ. И видимо будет лучше соответствовать, если к весам применить процедуру обработки подобную фМРТ.
Важность компрессии информации в мозге настолько велика, что существует даже подход к объяснению сознания и др. ментальных явлений, который основывается на этих представлениях, получивший название компрессионизма. Если приведенная работа является больше методологической, то в этой делается попытка ее некоторой реализации.
Удачи в исследованиях!

kraidiky
01.04.2024 14:32А можно подробнее про то, как в данном случае считается анизотропия в сигнале, и что более важно, как нормируется сигнал прежде чем её считать. Потому что центрирование на среднее очень контрпродуктивно если для сигнала характерно ненормальное распределение.
Например в AlexNet распределение logit-ов такое, что 3/4 значений меньше нуля, то есть активации ReLU будут в 3/4 случаев просто 0, а в остальных сигнал. Если такой треугольник относительно 0 отцентровать на среднее вы получите 3/4 одинаковых но не нулевых значений. Для других сетей у меня под рукой насчитанных активаций сейчас нет, вот тут можно графики посмотреть: https://t.me/GradientWitnesses/38, https://t.me/GradientWitnesses/39, но этот случай наводит на мысль.
Это может порождать проблемы, характерные для проблемы шкурки многомерного арбуза - в сильно многомерном пространстве обычная наша трехмерная интуиция ведёт к неправильным выводам.
Например: если у вас миллион логитов, матрица 1000x1000 и все они равны 0 и только по одному в каждой размерности равны 1, то эти вектора ортогональны интуитивно, но на сколько испортится картина если их отцентровать как-то? Интуитивно кажется, что не сильно.
Но если мы сделаем от такой матрицы активаций softmax как это делает multihead attention - то получим матрицу активаций в которой все элементы 0.001 кроме одного строки со значениями 0.027. Угол между этими двумя векторами - всего 4 градуса. А если миллион не один, а сто, то угол вообще может потеряться на фоне ошибки округления. Как вы справляетесь с этой проблемой?

kraidiky
01.04.2024 14:32+1Потому что если посмотреть на ситуацию с этой стороны, то рост анизотропии может свидетельствовать только о том, что Большая часть активаций не задействованы в каждом конкретном случае. А из этого могут следовать большие последствия - значительную часть сети можно не учитывать, а сети в процессе обучения сами стараются привести себя к "сигнальному" состоянию даже если об этом их никто специально не просил.

VDG
01.04.2024 14:32Не смотрели анизотропию для трансформера-декодера для эмбеддингов с выходов отдельно внимания и FFN?





YuriySeverinov
Год-два назад встречал статью, выводы которой заключались в том, что если продолжать учить модель длительное время после того, как она переобучилась, эффект переобучения постепенно начинает пропадать. В ней было сделано предположение, что модель начинает со временем выучивать не конкретные наблюдения, а реальные взаимосвязи и растет ее обобщающая способность.
Может этот эффект как раз и был связан с тем, что сперва модель формирует большое количество размерностей, а потом начинает их снижать?
Razant Автор
Вы говорите про явление Grokking. Да, похоже, что это явление и компрессия репрезентаций очень плотно связаны. Схожая интуиция была в статье про OmniGrok. Было бы очень интересно посмотреть что происходит с внутренней размерностью при переходе от оверфита к генерализации, предположу что там будет "ступенька" на графике внутренней размерности.
kraidiky
Ловите Ветрова, у которого есть грокнутые модели, на простых датасетах, берёте их погонять и прогоняете через свои метрики. Профит.