Привет! Меня зовут Дмитрий Королёв, я бэкенд-разработчик в Авито. В этой статье я расскажу про ключевые аспекты и концепции работы с наиболее популярными алгоритмами и структурами данных. Это поможет и в реальных проектах, и чтобы глубже понять алгоритмические принципы. Статья подойдёт специалистам, которые хотят углубить свои знания в программировании, и укрепить навыки нахождения оптимальных решений алгоритмических задач. 

Базовые концепции

Знакомство с алгоритмами и структурами данных лучше всего начать с двух базовых понятий: массивов и хэш-таблиц, причин для этого несколько:

• массивы и хеш таблицы есть в стандартной библиотеке большинства языков программирования

• массивы и хеш таблицы регулярно используются в повседневной работе

• массивы и хеш-таблицы - это две из самых простых и понятных структур данных

• многие(из личного опыта я бы даже сказал “большую часть”) алгоритмических собеседований можно пройти используя лишь массивы, хеш-таблицы и представленные ниже подходы к работе с ними

Массивы

Массив(списки в python) — это структура данных, представляющая собой коллекцию элементов одного типа, расположенных в памяти последовательно. Доступ к ним осуществляется по индексу. Массив занимает непрерывный участок памяти (это не всегда верно, но на этом уровне не будем закапываться в детали), и обычно имеют одинаковый тип данных. 

У каждого элемента массива — свой индекс, то есть порядковый номер внутри массива. Зная адрес начала массива и индекс элемента, мы всегда можем узнать адрес элемента массива в памяти: 

Подробнее можно почитать здесь.

Хеш-таблицы (они же мапы или словари)

Хеш-таблица — это структура для хранения данных в формате «ключ-значение». Внутренне хеш-таблицы обычно реализованы с использованием массива, где каждый элемент массива  — ещё одна структура данных, в которой хранятся элементы с одинаковым хешем. Например, это может быть массив или связный список.

Процесс добавления элемента в хеш-таблицу выглядит так:

1) Ключ пропускается через хеш-функцию, которая возвращает индекс в массиве для хранения значения.

2) Если по данному индексу уже есть элементы (это называется коллизией), то используется один из методов для разрешения коллизии, о которых расскажу ниже.

3) Если коллизий нет, элемент сохраняется по вычисленному индексу.

Коллизии возникают, когда два различных ключа преобразуются в один и тот же индекс массива при использовании хеш-функции. Это может произойти из-за ограниченного количества доступных индексов или из-за ограничений самой хеш-функции. Коллизии могут быть разрешены разными способами, здесь затронем два наиболее известных:

• метод цепочек (Chaining): В этом случае каждый элемент массива содержит структуру данных, в которую и будут добавляться все элементы с одинаковым хешем.

• открытое хеширование (Open Addressing): Этот метод позволяет помещать элементы прямо в массив. При возникновении коллизии он использует другие ячейки массива для поиска свободного слота (например, повторно пропускает результат, полученный после работы хеш функции, через хеш-функцию).

Пример работы хеш таблицы с методом цепочек

Подробнее можно почитать здесь.

Оценка сложности алгоритмов

Любая программа работает какое-то время и потребляет какое-то количество памяти. Для того, чтобы примерно оценить сложность работы, придумали такую штуку, как асимптотическая сложность. Это математическая модель, которая описывает поведение алгоритма относительно размера входных данных.

Асимптотика алгоритма определяет, как его эффективность изменяется с ростом размера входных данных. Обычно нас интересуют два аспекта: время выполнения и объем занимаемой памяти.

Рассмотрим пример:

def multiply_list(array, multiplier):
    new_array = []
    for i in array:
        new_array.append(i * multiplier)
    return new_array

• Во входных данных есть массив array переменной длины — обозначим его размер как N.

• Для оценки производительности алгоритмов используется O-нотация. С помощью неё и описывают асимптотическую сложность программы: она показывает, как время выполнения или используемая память алгоритма изменяются с увеличением размера входных данных. Например, O(N) означает линейный рост времени выполнения с увеличением размера данных, а O(N^2) — квадратичный рост. Это позволяет сравнивать алгоритмы и оценивать их эффективность на больших наборах данных, игнорируя меньшие детали.

• В данном случае время выполнения алгоритма составляет O(N), потому что количество операций прямо пропорционально размеру входных данных. Это достигается за счет итерации по массиву и выполнения операций умножения и добавления элемента в новый массив.

Аналогично, по оценке объема занимаемой памяти сложность также составляет O(N). Это обусловлено тем, что массив new_array увеличивается по мере добавления элементов, пропорционально длине входного массива.

Важно отметить, что константы в асимптотической сложности не существенны. Например, O(10) эквивалентно O(1), что подчеркивает, что асимптотика описывает скорость роста, игнорируя фиксированные коэффициенты.

Об оценке сложности алгоритмов написано уже очень много материала, поэтому здесь ограничимся этим одним маленьким примером, подробнее можно почитать в другой статье на хабре.

Сложности операций с массивами и хеш-таблицами

Напомню, что доступ по адресу в памяти осуществляется за O(1).

Сложности операций с массивами:

• Доступ к элементу: O(1) – поскольку, как выше было написано, зная индекс и адрес старта массива, мы знаем адрес элемента, а доступ к нему и происходит за O(1)

• Поиск элемента по значению: O(n) в общем случае, поскольку придется последовательно обойти все элементы массива (а его размер – N); в случае если массив отсортирован, то можно найти элемент за O(log n), если воспользоваться бинарным поиском.

• Вставка элемента в конец массива: в большинстве ЯП за счет автоматического управления расширения массивов сложность операции составляет O(1). Подробнее смотри тут — амортизационный анализ.

Вставка элемента в случайное место в массиве: O(n) т.к. придется полностью перевыделить память под массив.

Сложность операций с хеш-таблицами:

• Доступ по ключу: O(1), если коллизий нет; O(k), где k-число коллизий – если они есть.

• Поиск по ключу: O(1)/O(k), т.к. по сути это и есть просто доступ по ключу! :)

• Вставка: O(1)/O(k), также зависит от наличия коллизий.

Концепции при работе с массивами

Теперь мы рассмотрим три ключевые концепции при работе с массивами: два указателя, префиксные суммы и скользящее окно.

Мы изучим каждый метод на практических примерах решения алгоритмических задач. Такой подход поможет нам лучше понять суть каждого метода и научиться применять их в различных ситуациях.

Массивы: 2 указателя

Дан массив целых неотрицательных чисел, задача – переместить все нули в конец массива, сохраняя порядок остальных элементов. Пример: [0,3,0,1,12] –> [3,1,12,0,0]. Требуется найти решение за O(1) по памяти.

Идея: будем держать один указатель на позицию первого элемента со значением 0 и вторым указателем последовательно перебирать все элементы массива, при встрече элемента с ненулевым значением менять местами значения нулевого и ненулевого элементов. Таким образом мы переместим все нули в конец, рассмотрим по шагам на примере:

Шаг 1:

zero_elem_index = 0
non_zero_elem_index = 0
arr = [0,3,0,1,12]
zero_elem_index стоит на элементе со значением 0, не меняем его позицию
non_zero_elem_index стоит на элементе со значением 0, увеличиваем индекс на 1

Шаг 2:

zero_elem_index = 0
non_zero_elem_index = 1
arr = [0,3,0,1,12]
zero_elem_index стоит на элементе со значением 0, не меняем его позицию
non_zero_elem_index стоит на элементе со значением 1, меняем элементы местами 

Шаг 3:

zero_elem_index = 0
non_zero_elem_index = 1
arr = [3,0,0,1,12]
zero_elem_index стоит на элементе со значением 3, увеличиваем индекс на 1
non_zero_elem_index стоит на элементе со значением 0, увеличиваем индекс на 1

Шаг 4:

zero_elem_index = 1
non_zero_elem_index = 2
arr = [3,0,0,1,12]
zero_elem_index стоит на элементе со значением 0, ничего не делаем
non_zero_elem_index стоит на элементе со значением 0, увеличиваем индекс на 1

Шаг 5:

zero_elem_index = 1
non_zero_elem_index = 3
arr = [3,0,0,1,12]
zero_elem_index стоит на элементе со значением 0, ничего не делаем
non_zero_elem_index стоит на элементе со значением 1, меняем элементы местами 

Шаг 6:

zero_elem_index = 1
non_zero_elem_index = 3
arr = [3,1,0,0,12]
zero_elem_index стоит на элементе со значением 1, увеличиваем индекс на 1
non_zero_elem_index стоит на элементе со значением 1, увеличиваем индекс на 1

Шаг 7:

zero_elem_index = 2
non_zero_elem_index = 4
arr = [3,1,0,0,12]
zero_elem_index стоит на элементе со значением 0, ничего не делаем
non_zero_elem_index стоит на элементе со значением 12, меняем элементы местами

В итоге получаем отсортированный массив [3,1,12,0,0].

Гифка с другими входными задачами; синим указан zero_elem_index, красным non_zero_elem_index:

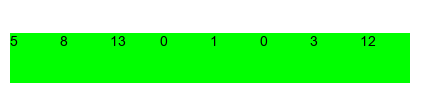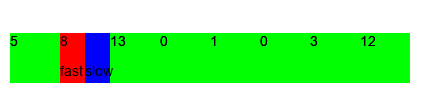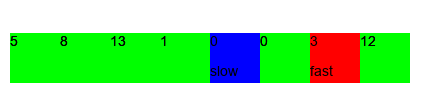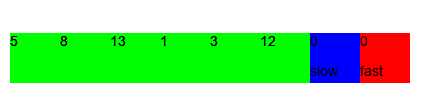
Основная концепция у двух указателей состоит в том, что есть два (а изредка и больше) указателей на определенные элементы, с которыми происходит какая-то логика. Также отличным примером служит бинарный поиск, позволяющий быстро (O(log n)) находить элементы в массиве.

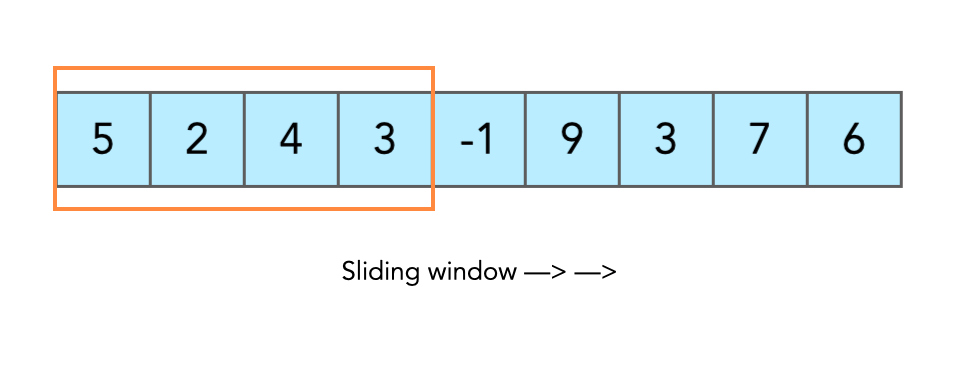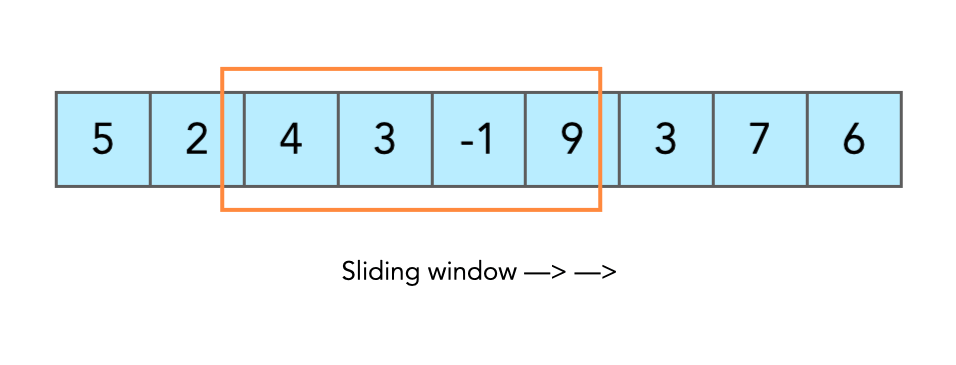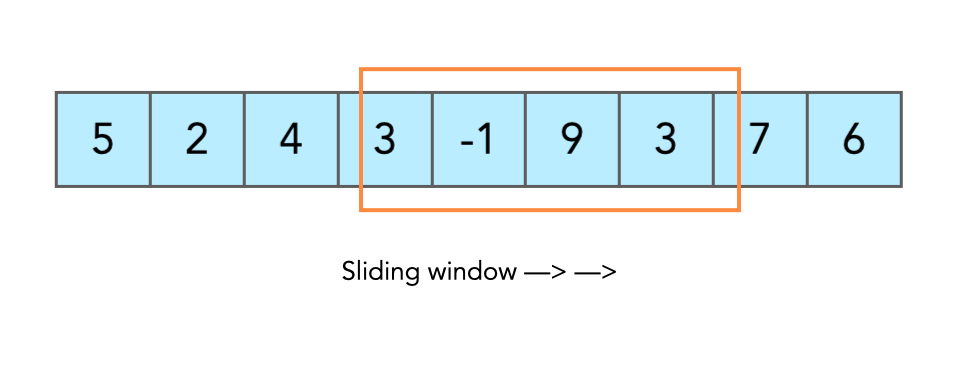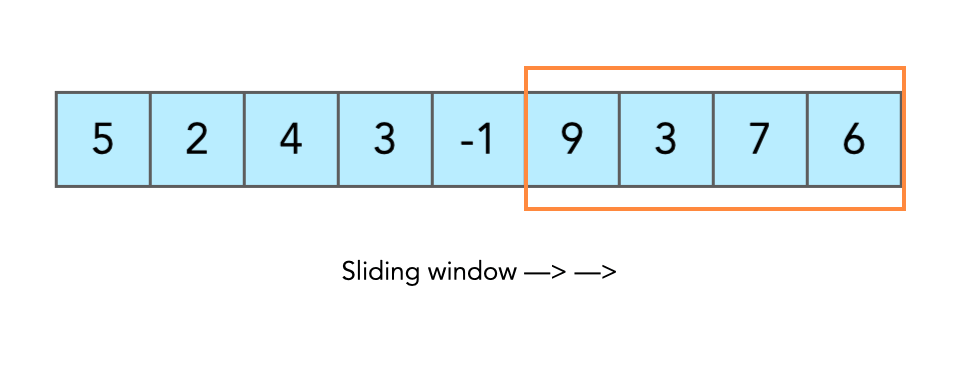
Массивы: скользящее окно

Скользящее окно — концепция, при которой мы работаем с фиксированным набором элементов последовательности данных. Это «окно» перемещается по последовательности, обрабатывая только те элементы, которые входят в его текущий диапазон. Таким образом, мы можем анализировать данные по частям, что часто бывает более эффективным и экономичным с точки зрения ресурсов.

Для лучшего понимания принципа работы скользящего окна, давайте рассмотрим его на примере массива чисел. Предположим, у нас есть массив:

data = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

Теперь создадим скользящее окно размером 3. Начнем с первых трех элементов массива:

[1, 2, 3]

Мы можем произвести какие-то операции над этими тремя элементами. Затем окно сдвигается на один элемент:

[2, 3, 4]

И мы снова выполняем операции. Процесс повторяется до тех пор, пока окно не достигнет конца последовательности. Обратите внимание на то, что в примере мы сдвинули как начало скользящего окна, так и его конец; однако мы можем, например, сдвигать сначала конец окна, а потом начало, в зависимости от задачи, которую предстоит решить. Этот метод позволяет нам эффективно обрабатывать большие объемы данных, не загружая память или процессор избыточной нагрузкой. 

Рассмотрим пример:

Дан массив nums, состоящий из нулей и единиц, и целое число k. Требуется вернуть длину максимальной последовательности единиц в массиве, если можно заменить не более k нулей на единицы.

Шаг 1: Инициализация переменных

def longest_consecutive_ones(nums, k):
    left, right = 0, 0
    max_length = 0
    zero_count = 0
    

left и right будут индексами левого и правого концов текущего скользящего окна.
max_length - длина максимальной последовательности единиц.
zero_count - количество нулей в текущем окне.

Шаг 2: Перемещение окна

while right < len(nums):
    if nums[right] == 0:
        zero_count += 1

Если текущий элемент – ноль, увеличиваем zero_count:

while zero_count > k:
    if nums[left] == 0:
        zero_count -= 1
        left += 1

Если zero_count превышает k, мы уменьшаем размер окна, сдвигая левый конец вправо до тех пор, пока zero_count не станет меньше или равным k:

 max_length = max(max_length, right - left + 1)

Обновляем max_length на основе текущего размера окна.

right += 1

Сдвигаем правый конец окна вправо.

Шаг 3: Возврат результата

    return max_length

Возвращаем максимальное количество последовательных единиц в массиве с учетом возможности замены не более k нулей.

Массивы: префиксные суммы

Префиксная сумма — подход, при котором предварительно вычисляются суммы элементов массива для быстрого получения суммы любого подмассива. Суть в том, чтобы сэкономить время на вычислениях, не пересчитывая сумму каждый раз заново.

Допустим, у нас есть массив чисел [1, 2, 3, 4, 5]. Префиксная сумма этого массива будет выглядеть следующим образом:

[1, 3, 6, 10, 15]

Каждый элемент нового массива — сумма элементов до текущего индекса включительно. Теперь, если мы хотим найти сумму элементов в подмассиве с индексами 2-4, мы можем просто вычесть сумму элементов до индекса 1 из суммы элементов до индекса 4:

Сумма[2-4] = Префикс[4] - Префикс[1] = 15 - 3 = 12

Рассмотрим пример кода, вычисляющего префиксную сумму:

def calculate_prefix_sum(arr):
    prefix_sum = [0] * len(arr)
    prefix_sum[0] = arr[0]

    # Вычисляем префиксную сумму
    for i in range(1, len(arr)):
        prefix_sum[i] = prefix_sum[i - 1] + arr[i]

    return prefix_sum

my_array = [1, 2, 3, 4, 5]
prefix_sum_array = calculate_prefix_sum(my_array)

# Теперь можем быстро найти сумму подмассива [2-4]: 
# prefix_sum_array[4] - prefix_sum_array[1]

Зачем это нужно? Префиксная сумма особенно полезна при работе с задачами, требующими частого вычисления суммы подмассивов. Это ускоряет выполнение кода и делает его более оптимизированным.

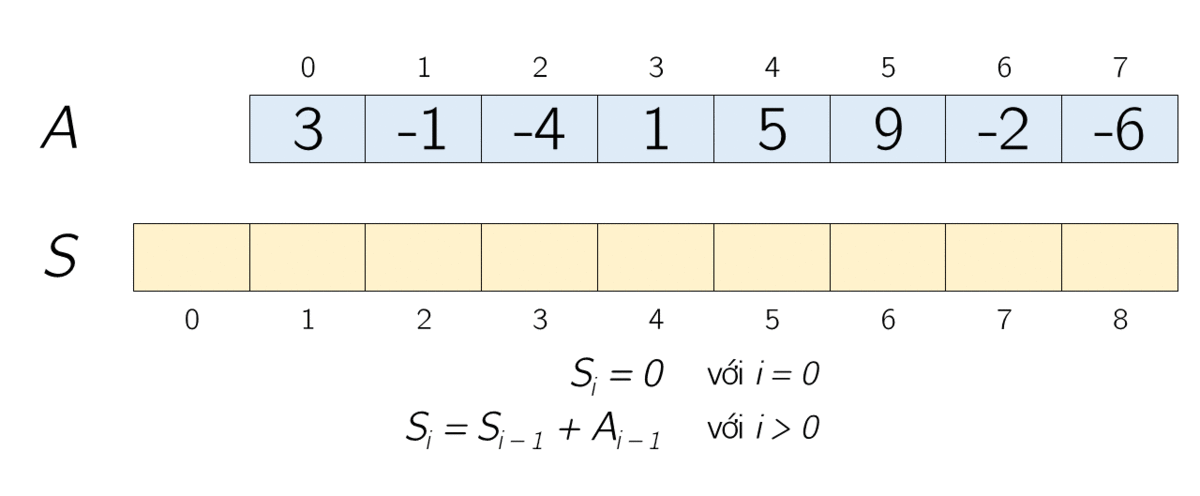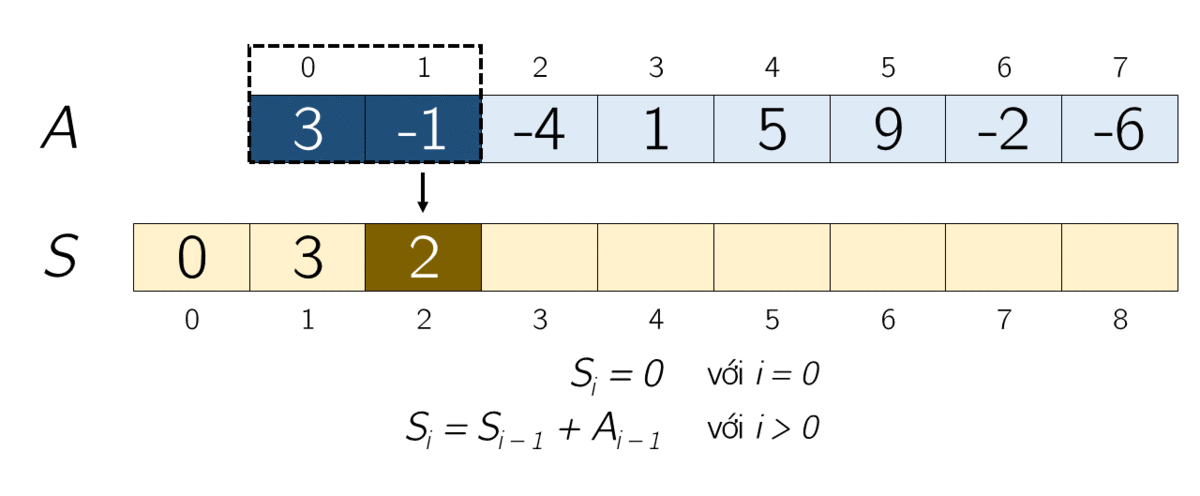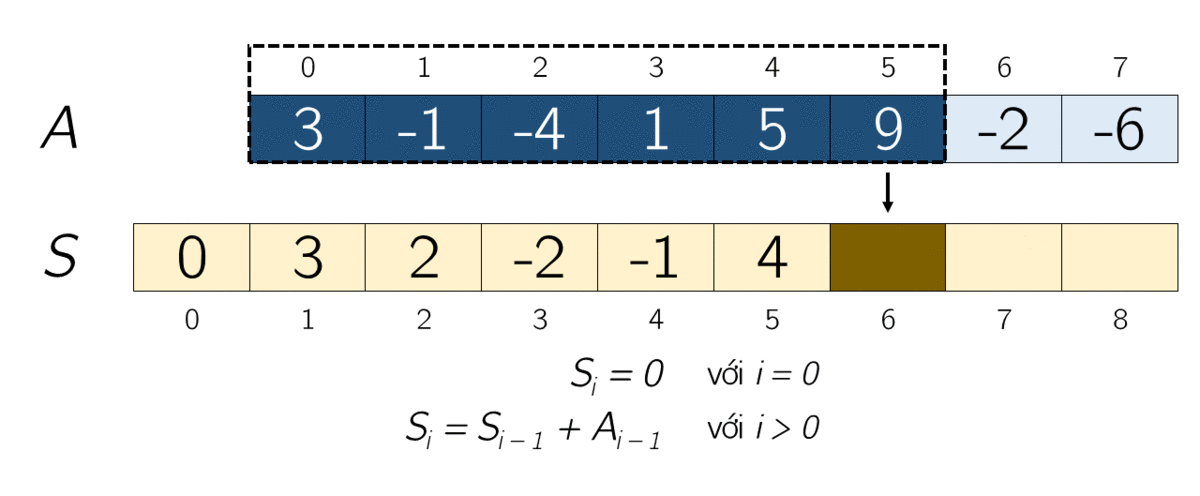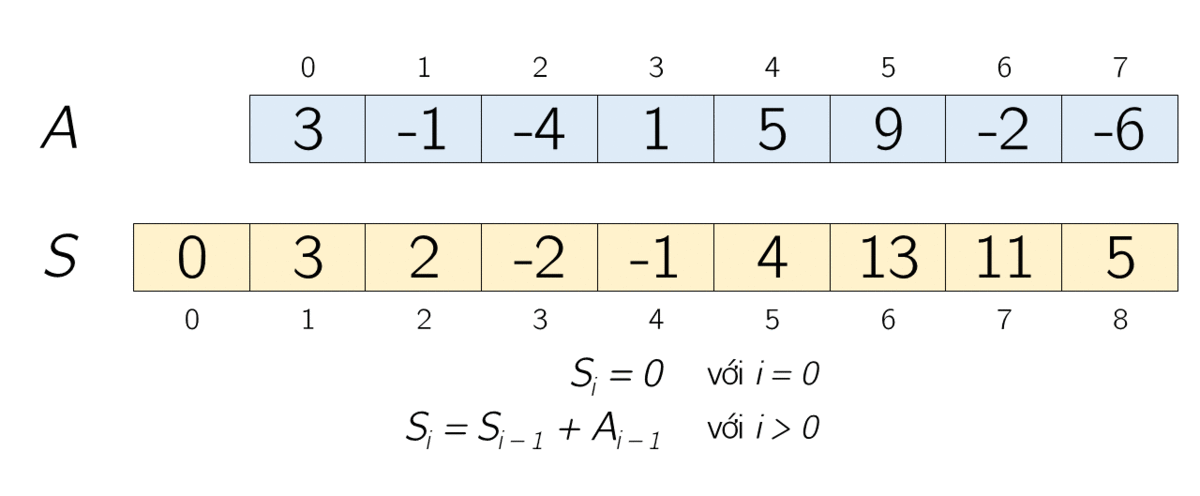
Хеш-таблицы

Хеш-таблицы: проверка наличия элемента

Один из самых популярных способов использования хеш-таблицы – проверка на наличие элемента во множестве. Хеш-таблица, в отличие от уже изученных в предыдущих постах массивов, может за O(1) сказать, содержится ли в ней элемент.

Рассмотрим пример задачи:

Панграмма – это предложение, в котором каждая буква английского алфавита встречается хотя бы один раз.

Дана строка, содержащая только строчные буквы английского языка. Верните список недостающих букв для того, чтобы строка считалась панграммой.

Пример:

Ввод: "abcdefghijklmnopqrstuvwx"

Вывод: ["y", "z"]

Решение:

Создадим строку alphabet, содержащую все буквы английского алфавита, и инициализируем хеш-таблицу letter_map. В этой хеш-таблице каждая буква алфавита является ключом, а значением является логическое значение False, показывающее, что на данный момент эта буква отсутствует в строке.

alphabet = "abcdefghijklmnopqrstuvwxyz"
letter_map = {letter: False for letter in alphabet}

Далее пройдем по каждому символу в строке sentence входных данных. Каждый встречающийся символ помечается в хеш-таблице letter_map как присутствующий, устанавливая значение ключа на True:

for char in sentence:
    letter_map[char] = True

Теперь создадим список missing, содержащий все ключи (буквы алфавита), у которых значение в letter_map осталось False, то есть буквы, отсутствующие в строке sentence входных данных.

После этих манипуляций остается только вернуть список недостающих букв

return missing

Хеш-таблицы: подсчет

Часто в задачах есть необходимость подсчитывать частоту встречаемости определенных элементов. Хеш-таблицы для этого идеально подходят, поскольку они позволяют дешево (O(1)) добавлять и удалять элементы.

Рассмотрим пример задачи:

Дана строка. Требуется проверить, имеют ли все символы входной строки одинаковое число вхождений.

Пример:

Ввод: "abacbca"

Вывод: false

В данной строке символ a встречается 3 раза, а символы b и c по 2 раза.

Решение:

Создадим пустой словарь char_count, который будет использоваться для подсчета количества вхождений каждого символа во входной строке.

def check_equal_occurrences(input_string):
    char_count = {}

Далее пройдем по каждому символу во входной строке input_string. Если символ уже присутствует в словаре char_count, будем увеличивать его счетчик на 1. Если символ встретился впервые, добавим его в словарь с начальным значением 1.

  for char in input_string:
        if char in char_count:
            char_count[char] += 1
        else:
            char_count[char] = 1

Создадим список occurrences, содержащий количество вхождений каждого символа из словаря char_count. Затем используем функцию all(), чтобы проверить, имеют ли все значения в этом списке одинаковое количество вхождений. Результат возвращается: True, если все значения равны, иначе False. Обратите внимание на то, что мы обращаемся таким образом к нулевому индексу списка occurrences; так что если в ограничениях задачи будет указано, что на вход может подаваться пустая строка – это нужно будет обработать отдельно.

occurrences = list(char_count.values())
    return all(count == occurrences[0] for count in occurrences)

Куда двигаться дальше в изучении алгоритмов и структур данных?

Чтобы глубже понимать, и эффективно применять алгоритмические концепции при решении реальных задач, стоит расширить свои знания, изучив дополнительные темы. Многие из них могут встречаться не так часто, но представляют собой более сложные и интересные вызовы, требующие не только знаний о массивах и хеш-таблицах. 

Графы. Графы представляют собой структуру данных, состоящую из узлов (вершин) и связей между ними (рёбер). Рёбра могут быть направленными и ненаправленными. Для глубокого понимания и эффективного использования графов важно знать о способах их представления (матрицы смежности, списки смежности), способах обхода графов (DFS — поиск в глубину, BFS — поиск в ширину). Также ценными являются знания о поиске кратчайших путей и выявлении циклов.

Стек/очередь/дек. Стек работает по принципу «последний вошёл, первый вышел» (LIFO), очередь — «первый вошёл, первый вышел» (FIFO), а дек (двусторонняя очередь) позволяет добавлять и удалять элементы как с начала, так и с конца. Эти структуры часто применяются как  вспомогательные средства в алгоритмах обработки данных, в системах управления задачами, а также в алгоритмах, требующих быстрого доступа к последним или первым элементам.

Односвязные и двусвязные списки. Это структуры данных, представляющие собой последовательность элементов, где каждый элемент содержит ссылку на следующий (односвязный) или на предыдущий и следующий элементы (двусвязный). Работа со списками часто требует вставки, удаления или обхода элементов. Также будет полезным умение переворачивать списки и определять наличие в них петель.

Жадные алгоритмы и динамическое программирование. Оба подхода используются для оптимизации решения задач, но имеют разные особенности. Жадные алгоритмы делают локально оптимальные выборы на каждом этапе с надеждой на глобальную оптимизацию. Динамическое программирование разбивает задачу на подзадачи и сохраняет результаты подзадач для повторного использования, чтобы избежать повторных вычислений. Эти методы находят широкое применение в разных областях, от разработки алгоритмов для решения сложных вычислительных задач до оптимизации процессов в системном проектировании.

Заключение

Надеюсь, что материал этой статьи был для вас не только занимателен, но и расширил ваше понимание ключевых концепций и техник работы с данными. По возможности оставьте ваше мнение о статье в комментариях) Спасибо вам за внимание и интерес к теме, и желаю удачи в применении полученных знаний в практической работе!