В последней третьей части обзора продемонстрировано, как на основе обобщённых типов-контейнеров реализуются различные ФП-техники “чистого” построения “эффективных” программ. В заключении будет отмечена роль теории категорий в обосновании важности абстракций, построенных над обобщёнными типами.

Оглавление обзора

• Часть 1

  • Обобщённые типы

  • Конструкторы типов

  • Полиморфные типы

  • Типы высокого рода

• Часть 2

  • Классы типов

  • Типы-контейнеры

• Часть 3 (данная публикация)

  • Контейнеры как фундамент для разработки

  • Подкатегории типов (вместо заключения)

Содержание третьей части

• Контейнеры как фундамент для разработки

  • Традиционный подход

  • “Читатель”

  • Свободный контейнер

  • Продолжения и алгебраические эффекты

  • Tagless Final

  • Клейсли и другие стре́лки

• Подкатегории типов (вместо заключения)

Контейнеры как фундамент для разработки

Сложные приложения декомпозируются на модули поменьше, которые традиционно называются сервисами, а в функциональной парадигме такие обобщённые сервисы часто называют “алгебрами”. Ключевой задачей является реализация высокоуровневых сервисов (в том числе и всей программы) посредством построения композиции вычислений из функций от других сервисов. Но, прежде всего, необходимо построить иерархию зависимостей сервисов и выбрать механизм их предоставления при реализации логики приложения.

Традиционный подход

Пожалуй, самым простым способом работы с зависимостями является их игнорирование, когда логика реализуется “в лоб” в статических методах. Термин “зависимости” в этом случае вообще не актуален – доступ к сторонним методам “импортируется” из других модулей, причём, зачастую, в самом начале файле, без привязки к целевому методу.

При функциональном подходе “сервисы” являются неизменяемыми, и их допустимо реализовывать в объектах-одиночках, не задумываясь о внедрении зависимостей. Это соответствуют идее “отказа от зависимостей”, когда они как эффекты обрабатываются в самом конце программы, а не в начале. Но, например, от зацикливания зависимостей такой подход не защищает. Более того, такой подход нарушает принцип “инверсии зависимости”, внося в код излишнюю связность, что в свою очередь приводит к нарушению более важно принципа “открытости/закрытости” и, как следствие, издержкам в сопровождении этого кода.

В ООП хорошим тоном считается описание сервиса в виде абстрактного интерфейса (trait в Scala), классы-реализации которого принимают другие сервисы-зависимости в своём конструкторе:

trait Service1 { def func1(d: Double): Int    }
trait Service2 { def func2(i: Int)   : String }
trait Service3 { def func3(d: Double): String }

// "инъекция" зависимостей через конструктор
final case class Service3Impl(srv1: Service1, srv2: Service2) extends Service3:
  override def func3(d: Double) = srv2.func2(srv1.func1(d))

В реализации Service3 используется композиция возможностей func1 и func2 сервисов Service1 и Service2. Но чтобы выполнить эту композицию, необходимо сперва представить экземпляры сервисов-зависимостей:

val srv1: Service1 = ???
val srv2: Service2 = ???

val srv3: Service3 = Service3Impl(srv1, srv2)
srv3.func3(4.2)

При большом количестве сервисов со сложной многоуровневой иерархией такой наивный подход приводит к “вскипанию” кода со всеми сопутствующими проблемами. В Scala для упрощения такого рода инъекций используют библиотеку MacWire – макросы автоматически генерируют вызов конструкторов, а также рекурсивно ищут и подставляют в конструкторы значения уже их зависимостей. Если же вдруг какая-то зависимость не найдена, об этом становится известно на этапе компиляции.

Во многих других языках стандартным решением является использование DI-контейнеров (dependency injection container). Туда предварительно регистрируются классы-реализации сервисов, а в дальнейшем, на запрос по типу какого-либо верхнеуровневого сервиса, контейнер сам сконструирует этот экземпляр, используя все найденные зависимости (и зависимости этих зависимостей, и т.п.). Особенностью многих DI-контейнеров является возможность управлять созданием и временем жизни экземпляров сервисов. Например, можно потребовать, чтобы сервисы создавались при каждом запросе к контейнеру, или единственный раз при первом обращении. Также зачастую DI-контейнеры защищают от зацикливания зависимостей.

Проблема большинства DI-контейнеров заключается в том, что проверка наличия всех необходимых зависимостей в иерархии производится в процессе выполнения. Значит остаётся вероятность, что ошибки, связанные с зависимостями, сможет обнаружить только конечный пользователь.

В Scala в качестве DI-контейнера могут выступать контекстные абстракции. Механизм вывода термов позволяет явно или неявно извлекать из контекста экземпляры нужного типа:

given Service1 = new Service1 { override def func1(d: Double) = ??? }
given Service2 = new Service2 { override def func2(i: Int   ) = ??? }

object Service3:
   def instance(using srv1: Service1, srv2: Service2) = Service3Impl(srv1, srv2)

Service3.instance.func3(4.2)

В последней строчке при обращении к instance будут найдены в контексте и неявно переданы как аргументы экземпляры сервисов Service1 и Service2, так как в определении функции эти аргументы указаны с ключевым словом using. Если же по какой-либо причине в момент вызова instance контекст не будет содержать значения нужных типов, то компилятор выдаст ошибку – проверка корректности иерархии зависимостей осуществляется средствами языка на этапе компиляции, причём без использования макросов!

Cake pattern

Далее будут рассмотрены техники, основанные на контейнерных типах, но ради справедливости стоит упомянуть ещё одну, известную под названием Cake pattern. В этом подходе сервисы-зависимости описываются как трейты с уже реализованными методами, а непосредственно инъекция в верхнеуровневый сервис осуществляется посредством расширения этого сервиса теми самыми трейтами. Cake-pattern базируется на полиморфизме подтипов, но для него не требуются использовать обобщённые типы, поэтому в данной статье не будет подробностей об этом. Кроме того, такой подход имеет ряд принципиальных недостатков (см., например, статью Cake antipattern), и в настоящее время его использование не рекомендуется.

Помимо построения иерархии зависимостей компонентов приложения, нужно также решить задачу композиции предоставляемых ими функций. Тривиальное решение из примера выше оказывается недостаточным, если нужна более оптимальная работа с потоками вычислений, “чистая” работа с эффектами и т.п. Тут выручают контейнерные типы с соответствующим образом реализованными контейнерными возможностями.

В Scala таким контейнером эффектов, в первую очередь, являлся встроенный Future. Он позволяет распределять вычисления по отдельным потокам, тем самым снижая потребление ресурсов компьютера. Но его “жадный” характер снижает возможности статической проверки корректности программы. Эту проблему могут решить такие “ленивые” контейнеры, как IO из Cats, ZIO из одноимённой библиотеки, Task из чуть менее популярной библиотеки Monix.

На практике наиболее востребованы такие возможности, которые позволяют комбинировать эффективные функции. По этому представленные ранее контейнерные возможности часто комбинируются в более сложных классах типов, что-то вроде таких:

type Functor    [F[_]] = [A, B] =>  (A =>   B)  => (F[A] => F[B]) // Lift
type Applicative[F[_]] = [A, B] => F[A =>   B]  => (F[A] => F[B]) // Lift & Zip2
type Monad      [F[_]] = [A, B] =>  (A => F[B]) => (F[A] => F[B]) // Lift & Flatten

Такая запись показывает схожесть этих возможностей, нацеленность их на комбинирование различных эффектов, объединённым одним контейнером F[_]. В частности, Applicative отвечает за независимое вычисление эффектов, в то время как Monad – за последовательное. Это, например, означает, что при комбинировании посредством Monad вычисления выстраиваются в цепочку, и сбой в любом звене приведёт к её разрыву, и остальные вычисления не будут выполнены. Вот типичный фрагмент программы на базе контейнера IO:

import cats.effect.IO
import cats.syntax.all.*
//                                                реализации шагов не важны
def findTheKeys:        Clue          => IO[Keys]  = ???
def obtainPart1:        Keys          => IO[Part1] = ???
def obtainPart2:        Keys          => IO[Part2] = ???
def completeThePuzzle: (Part1, Part2) => Treasure  = ???

def findTheTreasure(someClue: Clue) =
  findTheKeys(someClue)
    .flatMap(keys => obtainPart1(keys) product obtainPart2(keys)) 
    .map(completeThePuzzle.tupled)

Возможности комбинирования здесь предоставляются реализациями классов типов для контейнера IO:

• map Functor,

• product Applicative,

• flatMap Monad.

В каких-то командах разработчики предпочитают более императивный стиль, основанный на использовании for-выражений:

def findTheTreasure(someClue: Clue) =
  for {
    keys  <- findTheKeys(someClue)
    part1 <- obtainPart1(keys)
    part2 <- obtainPart2(keys)
  } yield completeThePuzzle(part1, part2)

For-выражения представляют собой “синтаксический сахар”, который на этапе предкомпиляции раскрывается в цепочку вызовов тех же map, flatMap. Например, вызов map спрятан здесь в последней строчке с yield, а возможности Applicative вообще не задействованы – вместо этого используется дополнительный вызов flatMap и, если не удастся получить part1, то вычисление part2 даже не начнётся.

Какой бы стиль ни был выбран, основная суть традиционного подхода остаётся прежней – зависимости инъектируются (зачастую, неявно) в конструкторы классов, в методах которых используются обобщённые контейнерные типы для более удобной (и, по возможности, чистой!) композиции эффективных вычислений. Использование вывода термов для инъекции зависимостей и возвращение значений в контейнере Future/IO/ZIO/Task выглядят как минимальный набор для построения Scala-программы. Но иногда встречаются задачи, требующие более сложных решений. Далее будут рассмотрены несколько таких примеров.

“Читатель”

Вычисление зависимостей и передача их в бизнес-логику является типичным шаблонном, просматривающимся во всех фрагментах приложения. Это не основная, а вспомогательная сквозная логика, на которой не стоило бы акцентировать внимание. А ведь именно и происходит в ОПП-шной инъекции зависимостей, когда сервисы вычисляются и передаются функциям перед их вычислением. Перенести всю возню с зависимостями в самый конец вычислений помогает шаблон “читатель” (reader).

Давайте снова вернёмся к сценарию “избавления от зависимости”, упомянутому в самом начале статьи. Вот типичный ООП-шный класс, принимающий в конструктор сервис-зависимость:

trait Dep
final case class ServiceImpl(dep: Dep):
  def func(d: Double): String = ???

Зависимость dep: Dep передаётся в конструктор класса только для того, чтобы её можно было использовать при реализации его функций. Иначе говоря, класс – это лишь набор функций, для которых сперва должны быть предоставлены все зависимости как параметры. Выразим это утверждение явно на примере одной функции и произведём пару манипуляций:

def func_1(dep: Dep)(d: Double)    =  ???
//  ⇓⇓⇓⇓⇓⇓ вследствие алгебраического изоморфизма типов (Aᴮ)ᴰ ≡ (Aᴰ)ᴮ
def func_2(d: Double)(dep: Dep)    =  ???
//  ⇓⇓⇓⇓⇓⇓ можно считать, что это просто иная запись func_2
def func_3(d: Double) = (dep: Dep) => ???

Функция func_3, принимая значение Double возвращает другую функцию от значения Dep. Теперь вычисление функции func_3 не требует предварительной передачи зависимости Dep:

val packedRes = func_3(4.2)  // Dep => Srting

И только после этого подставляются зависимости:

val dep = new Dep{}
val finalRes = packedRes(dep) // String

Основная логика приложения никак не изменилась, но с помощью простых алгебраических изоморфизмов типов получилось вынести упомянутую ранее вспомогательную логику по вычислению и передаче зависимостей в самый конец!

Выразим явно обобщённый тип результата func_3:

type Reader[D] = [A] =>> D => A
type ReaderDep[A] = Reader[Dep][A]
def func_3(d: Double): ReaderDep[String] = ???

Обобщённый тип Reader основан на стандартном функциональном типе Scala, который, очевидно, является контейнерным по типу результата. Для него уже реализованы “контейнерные” возможности map, flatMap, следовательно, можно стоить композиции функций вида func_3, возвращающих значения в контейнере ReaderDep[_].

Тип Reader сам по себе не решает задачу композиции эффективных вычислений. Но тут выручает основанный на нём трансформер:

type ReaderT[F[_], D] = [A] =>> Reader[D][F[A]] // D => F[A]

Контейнер F[_] является носителем произвольных эффектов, а трансформер над ним транслирует возможности комбинирования эффективных функций.

В библиотеке Cats похожим образом определён тип ReaderT. Особенности реализации его контейнерных возможностей требуют, чтобы у комбинируемых функций были “зависимости” одного и того же типа (в примере выше это trait Dep). Для этого иногда посредством наследования (расширения) строится общий тип, объединяющий все возможные зависимости комбинируемых функций, выбирается контейнер эффектов и на этой основе строится свой:

import cats.data.ReaderT                    // импортируется трансформер
import cats.effect.IO                       // импортируется какой-то контейнер эффетов

trait Dep1; trait Dep2                      // исходные сервисы-зависимости
type TotalDep = Dep1 & Dep2                 // общая "жирная" зависимость как пересеченеи типов
type ReaderIO[A] = ReaderT[IO, TotalDep, A] // итоговый контейнер

Необходимость ручного построения такой “жирной зависимости” ограничивает разработку приложения. Альтернативой может быть множественное “наслоение” ReaderT, распаковка которого потребует точно соблюдения порядка передачи зависимостей.

Более удобное решение предлагает вторая версия библиотеки ZIO. Как уже упоминалось ранее, одноимённый контейнер может интерпретироваться как применение трансформера ReaderT. Например, построим функцию, реализация которой зависит от сервисов Dep1 и Dep1:

def func(d: Double) = for {
  dep1 <- ZIO.service[Dep1]
  dep2 <- ZIO.service[Dep2]
} yield (??? : String) // тут используются d, dep1, dep2

Её можно вызвать сразу:

val packedRes = func(4.2) // ZIO[Dep1 & Dep2, Nothing, String]

Как и с контейнером ReaderT, зависимости можно предоставить в дальнейшем:

val dep1Layer = ZLayer.succeed(new Dep1{}) 
val dep2Layer = ZLayer.succeed(new Dep2{})

val zioRes = packedRes.provide(dep2Layer, dep1Layer) // ZIO[Any, Nothing, String]

Итоговое значение zioRes уже не имеет зависимостей, оно лишь упаковано в контейнер эффектов, аналогичный cats.IO[_].

Особенностью такого подхода является то, что зависимости могут быть предоставлены в произвольном порядке и не обязательно одновременно. “Слои” (layers) намекают на то, что иерархия зависимости может быть дополнительно структурирована.

Итак, шаблон “читатель” переносит предоставление зависимостей на финальный этап вычислений. На первоначальном этапе остаётся построение функции, принимающей эти зависимости. Стоит заметить, что таким способом первый этап можно сделать “чистым”, без побочных эффектов. Схожими особенностями обладают и другие “контейнерные” подходы, представленные далее – сперва идёт “чистое” построение композиции вычислений внутри некого контейнера, и лишь в самом конце при распаковке требуются реализации зависимостей.

Свободный контейнер

Рассмотрим такой обобщённый тип:

enum Freee[F[_], A]:
  case Pure   [F[_], A](a: A)              extends Freee[F, A]
  case Suspend[F[_], A](a: F[Freee[F, A]]) extends Freee[F, A]

Утверждается, что типы Freee[F, A] и F[A] изоморфны для любых A и ковариантного F[+_]. Доказательство утверждения, как и само происхождение этого рекурсивного типа выходит за рамки данной статьи, здесь мы изучим лишь некоторые его свойства.

Имея возможность map для F[_], можем "поднять" её и до Freee, например, добавив этот метод в enum:

def map[B](f: A => B)(using Lift[F]): Freee[F, B] = this match // this: Freee[F, A] - мы же внутри enum
  case Pure(a)     => Pure(f(a))
  case Suspend(fa) => Suspend(fa.map(_.map(f)))

Здесь использован класс контейнерных типов Lift, введённый в этой статье ранее – он позволяет вызвать map для fa в последней строчке.

Но гораздо интереснее то, как мы можем определить “разметрёшивание” Freee:

import Freee.*
extension [F[_]: Lift, A](ffa: Freee[F, Freee[F, A]])
  def flatten: Freee[F, A] = ffa match
    case Pure(fa) => fa
    case Suspend(a) => Suspend(a.map(_.flatten))

Обратите внимание на то, что наличие возможностей контейнера F[_] вроде flatten, или flatmap не требуется. Получается что, ввиду заявленного изоморфизма с F[_], Freee обогащает исходный ковариантный контейнер возможностью “разматрёшивания”!

Примеры использования будут далее, а сейчас попробуем попробуем избавится от назойливого требования F[_]: Lift, которое необходимо для композиции вычислений посредством Freee. Оказывается, для этого достаточно в тип-сумму Freee добавить ещё одно слагаемое, получив “более свободный“ контейнер Freer:

enum Freer[F[_], A]:
  case Pure   [F[_], A](a: A)                                      extends Freer[F, A]
  case Suspend[F[_], A](a: F[Freer[F, A]])                         extends Freer[F, A]
  case FlatMap[F[_], A, B](fb: Freer[F, B], afb: B => Freer[F, A]) extends Freer[F, A]

import Freer.*

extension [F[_], A](ffa: Freer[F, A])
  def map[B](f: A => B): Freer[F, B] = FlatMap(ffa, f andThen Pure.apply)
  def flatMap[B](f: A => Freer[F, B]): Freer[F, B] = FlatMap(ffa, f)

extension [F[_], A](ffa: Freer[F, Freer[F, A]])
  def flatten: Freer[F, A] = FlatMap(ffa, identity)

Теперь можно строить композицию вычислений с носителем эффектов F, при этом даже не ожидая, что для него предоставлены контейнерные возможности! Распаковку Freer можно реализовать так:

extension [F[_], A](ffa: Freer[F, A])
  def go(extract: [X] => F[Freer[F, X]] => Freer[F, X])(using Lift[F]): A =
    ffa match
      case Pure(fa)         => fa
      case Suspend(ffa)     => extract(ffa) go extract
      case FlatMap(fb, bfa) => bfa(fb go extract) go extract

В чём же выгода, если для распаковки Freer всё равно потребуются контейнерные возможности F? Хитрость заключается в том, что распаковаться можно в совсем другой контейнер! Такая функция, зачастую, называется foldMap и требует контейнерные возможности для нового контейнера G[_]; позаимствуем их из класса типов cats.Monad:

import cats.Monad
import cats.syntax.all.*

extension [F[_], A](ffa: Freer[F, A])
  def foldMap[G[_]: Monad](fToG: F ~> G): G[A] = ffa match
    case Return(a)      => Monad[G].pure(a)                            // pure    из Monad[G]
    case Suspend(ma)    => fToG(ma).flatMap(_ foldMap fToG)            // flatMap из Monad[G]
    case FlatMap(fa, f) => fa.foldMap(fToG).flatMap(f(_) foldMap fToG) // flatMap из Monad[G]

Это полностью освобождает от ограничений на F[_] – можно использовать произвольные обобщённые типы в качестве описания бизнес-эффектов. Остаётся лишь в самом конце предоставить “естественные“ преобразования ~> из этих бизнесовых контейнеров в универсальные, вроде IO. Класс Free[F[_], _] представляет собой контейнерный трансформер, но его не правильно называть “монадным”, как аналогичные типы из раздела выше, потому что в качестве F[_] он принимает любой контейнер, даже без явных “монадных” возможностей, вроде flatMap – вообще никакие ограничения на исходный контейнер не накладываются!

Реализация “более свободного” контейнера Freer присутствует в библиотеке Cats под именем Free. Разберём его особенности на примере композиции таких элементов (чистое значение и функция):

val initVal: Future[Int] = Future.successful(21)
def effectiveFunc(i: Int)(using ExecutionContext): Future[Int] =
  Future {
    val intRes = i * 2
    println(s"$i => $intRes")
    intRes
  }

Соберём из них простенькую программу, “подняв” исходные элементы, определённые через контейнер Future[_], в “мир” трансформированного контейнера Free[Future, _] из библиотеки Cats с помощью функции Free.liftF:

val freeInitVal       = Free.liftF(initVal)              // поднимаем значение
val freeEffectiveFunc = effectiveFunc andThen Free.liftF // поднимаем функцию (у liftF есть нужная перегрузка)
def buildFreeProgram(using ExecutionContext): Free[Future, Int] =
  freeInitVal
    .flatMap(freeEffectiveFunc)
    .flatMap(freeEffectiveFunc) // просто по-приколу, вызываем ту же функцию ещё раз

Для Free конечно же реализованы ключевые возможности контейнеров, позволяющие строить композицию “эффективных” вычислений, и пока не заметно отличий от исходного контейнера Future . Они проявятся позднее, когда будет вызвана функция freeProgram и произведена “распаковка” результата.

Для распаковки можно воспользоваться методом def go(f: S[Free[S, A]] => Free[S, A])(implicit S: Functor[S]): A:

given ExecutionContext = ExecutionContext.global
import cats.instances.future.catsStdInstancesForFuture // импорт неявного Functor[Future]

def extractFuture[A]: Future[A] => A =
  Await.result(_, Duration.Inf)

val freeProgram = buildFreeProgram // "конструируем" программу

// и выполняем её вычисление (распаковку) дважды:
val res1 = freeProgram go extractFuture // (using Functor[Future]), так как "под капотом" нужен map
val res2 = freeProgram go extractFuture // (using Functor[Future]), так как "под капотом" нужен map
print(res1, res2)

Выполнение этого кода приведёт к такому выводу на консоль:

21 => 42
42 => 84
21 => 42
42 => 84
(84,84)

Не смотря на то, что контейнер Future является “жадным”, трансформация с помощью в Free даёт “ленивый” контейнер, как представленный ранее IO – все внутренние вычисления откладываются на этап распаковки. Именно поэтому побочные эффекты (вывод на консоль строчек вида x => y) сработали дважды – при распаковке в переменные res1 и res2. Для распаковки Free требуются возможности вложенного контейнера. В примере выше это extractFuture: Future[A] => A и map из неявного значения класса типа Functor[Future], предоставляемого библиотекой Cats.

Более интересен второй способ распаковки, основанный на foldMap:

def extractFuture[A]: Future[A] => A =
  Await.result(_, Duration.Inf)

val interpreter: Future ~> Id =           // "естественное" преобразование контейнеров
  FunctionK.lift{ [X] => (fx: Future[X]) => extractFuture(fx) }

val res = freeProgram foldMap interpreter // неявно используется Monad[Id] для flatMap, который
println(res)                              // нужен для ленивой хвостовой рекурсии

Такая особенность трансформера Free позволяет использовать элегантный трюк для декомпозиции бизнес-логики приложения на отдельные блоки. Ранее уже упоминалось, что с контейнерным типом можно связать те или иные эффекты. Эффекты завязаны не столько на устройстве самого обобщённого типа (какие поля и как именно размещены в памяти), сколько на реализацией его “контейнерных функций” – запаковки, внутренних преобразований, перепаковки в другие контейнеры и, в частности, распаковки. Это даёт возможность строить чистую композицию эффективных вычислений. Но трансформер Free позволяет достичь того же результата с контейнерами, для которых эти возможности даже не заданы изначально, а следовательно, и эффекты не определены. Их, конечно, придётся конкретизировать для распаковки Free, но до этого момента исходный контейнер считается совершенно абстрактным. Иными словами, свободный контейнер позволяет абстрагироваться от эффектов.

Рассмотрим следующий пример. Допустим, нужно описать функции взаимодействия с репозиторием пользователей. Используя эти типы

type UserId    = Int
type UserInfo  = String
type UserSaved = Unit

нужно определить операции

type GetUser = UserId => Option[UserInfo]
type PutUser = (UserId, UserInfo) => UserSaved
type ListAll = Unit => List[(UserId, UserInfo)]

Проблема в том, что такие функции не могут быть “чистыми”, так как они работают с изменчивым состоянием хранилища – это “эффективные” функции. Чтобы сделать их “чистыми”, они должны возвращать результат в некотором контейнере, чья “распаковка” вызывала бы срабатывание соответствующих эффектов. Традиционно такие функции реализуются через соотношение подтипизации для слагаемых обобщённого алгебраического типа:

enum UsersRepository[A]:
  case Get(id: UserId)                 extends UsersRepository[Option[UserInfo]]
  case Put(id: UserId, user: UserInfo) extends UsersRepository[UserSaved]
  case ListAll                         extends UsersRepository[List[(UserId, UserInfo)]]

Контейнерный тип UsersRepository[_] соответствует эффекту работы с репозиторием, но не имеет ничего, кроме функций неявно приведения к себе от своих подтипов-слагаемых. Он является носителем абстрактного эффекта.

Для удобства композиции вычислений, часто вводятся вспомогательные функции, своего рода синтаксический мусор сахар:

import UsersRepository.*
type FreeUsersRepo[X] = Free[UsersRepository, Option[UserInfo]] // псевдоним для наглядности
def liftUserRepo = cats.free.Free.liftK[UsersRepository]        // UsersRepository ~> FreeUsersRepo

def getUser(id: UserId)                : FreeUsersRepo[Option[UserInfo]] = liftUserRepo(Get(id))
def putUser(id: UserId)(user: UserInfo): FreeUsersRepo[Unit]             = liftUserRepo(Put(id, user))
def listUsers                          : FreeUsersRepo[List[UserInfo]]   = liftUserRepo(ListAll)

Аннотации типов излишни. Они лишь подчёркивают, что функции возвращают значения в свободном контейнере над трансформированным UsersRepository. Из этих “освобождённых” функций можно построить композицию для реализации произвольной бизнес-логики:

import cats.syntax.all.*
val program = // FreeUsersRepo[List[(UserId, UserInfo)]]
  putUser(42)("answer") >>
  listUsers

Здесь >> – это лишь псевдоним из Cats для flatMap, в котором игнорируется аргумент (“произведение эффектов”, при котором учитывается только “правый“ результат). Переменная program содержит описание композиции функций с неизвестным ещё эффектом. Чтобы эту программу “запустить”, нужно знать, как интерпретировать исходный абстрактный контейнер UsersRepository, как преобразовать его к другому контейнеру с учётом специфичных эффектов:

import cats.arrow.FunctionK.{lift as liftTransform}
import cats.{Id, ~>}
import scala.collection.mutable.{Map as MutMap}

val usersRepoInterpreter: UsersRepository ~> Id = {
  val storage = MutMap.empty[UserId, UserInfo]
  liftTransform{[A] => (fa: UsersRepository[A]) =>
    {fa match
      case Get(id)       => storage.get(id)
      case Put(id, user) => storage.addOne(id, user)
      case ListAll       => storage.toList
    }.asInstanceOf[A] // а ведь компилятор и сам мог бы догадаться...
  }
}

program foldMap usersRepoInterpreter // List((24,rewsna), (42,answer))

Здорово! Но в настоящей программе приходится работать с разными эффектами одновременно. К примеру, добавим ещё такие:

enum SearchServcie[A]:
  case SearchBest (request: String) extends DataServcie[String]
  case FindSeveral(request: String) extends DataServcie[List[(Relevance, String)]]

enum NotificationService[A]:
  case Send(notification: String) extends NotificationService[NotificationResult]

Теперь для построения композиции нужно “освободить” контейнер, который сочетал бы все эти эффекты. Для этого библиотека Cats предлагает тип EitherK вида . Это не просто трансформер контейнеров, но их комбинатор. С его помощью можно сформировать контейнер для всех эффектов:

import cats.data.EitherK
type :+:[F[_], G[_]] = [A] =>> EitherK[F, G, A] // лево-ассоциативный оператор над типами-контейнерами
type TotalAlgebra[A] = (
  UsersRepository     :+:
  SearchServcie       :+:
  NotificationService
)[A]

Лево-ассоциативные операторы, вроде введённого тут :+: заметно упрощают работу со свободными контейнерами. Аналогичное решение, а также другие плюшки для работы со свободными контейнерами встречаются в различных библиотеках, например, во Freek.

Контейнеры, подобные представленному выше TotalAlgebra, действительно иногда называются “алгебрами” над типом-параметром, потому что, как и в академической математике, они описывают N-арные операции для переменных разных типов, в том числе и типа-параметра (даже если операция только возвращает значение этого типа).

“Сахарные” функции нужно теперь поднимать до TotalAlgebra:

import SearchServcie.*
import NotificationService.*

def liftF = cats.free.Free.liftInject[TotalAlgebra]

def searchBest      (request: String)            = liftF(SearchBest (request))
def findSeveral     (request: String)            = liftF(FindSeveral(request))
def sendNotification(notification: Notification) = liftF(Send(notification))

Конечно, также придётся переписать аналогичные функции для UsersRepository. Функция liftInject принимает неявный параметр типа InjectK[Big[_], Small[_]], который, по сути, предоставляет “естественное” преобразование от контейнера Small к Big. В библиотеке Cats уже есть неявные значения InjectK с комбинатором or для контейнеров, связанных посредством EitherK.

Подготовив аналогично usersRepoInterpreter интерпретаторы dataServcieInterpreter notificationInterpreter можно собрать полный с помощью or (важно соблюсти порядок комбинации контейнеров в TotalAlgebra):

def searchServcieInterpreter: SearchServcie       ~> Id = // какая-то реализация
def notificationInterpreter : NotificationService ~> Id = // какая-то реализация

extension[F[_], G[_]](fg: F ~> G)
  def :+:[H[_]]      (hg: H ~> G) = fg or hg // лево-ассоциативный синоним для or

def totalInterpreter =
  usersRepoInterpreter     :+:
  searchServcieInterpreter :+:
  notificationInterpreter

И теперь можно писать уже вот такие большие программы ?:

val littleBigProgram =
  searchBest("best user")           productL
  sendNotification("user captured") flatMap
  putUser(42)                       productR
  getUser(42)                       map
  {_.fold("")(_.reverse)}           flatMap // перворачиваем имя в обратном порядке. Типа, так заказчик захотел)))
  putUser(24)                       productR
  listUsers

littleBigProgram foldMap totalInterpreter

Такая техника интересна тем, что позволяет создавать программы-как-данные. Единожды собранную программу можно модифицировать и интерпретировать разными способами. Помимо преобразования свободного контейнера в Id, полезными бывают также преобразования в Either (для модульных тестов), или всякие Future (забудьте) IO, ZIO (для самого продукта). На практике всё же такая возможность Free редко бывает востребованной. Однако, свободные контейнеры используются не только для компоновки больших приложений, но и в некоторых библиотечных инструментах. Например, в библиотеке doobie есть type ConnectionIO[A] = Free[ConnectionOp, A] – надстройка над ConnectionOp, обобщённой сумой типов, олицетворяющих различные JDBC-операции.

Вот список дополнительной литературы об устройстве и применении контейнера Free.

• Русскоязычные публикации на Хабре:

  • Scala: Гексагональная архитектура и DDD на Free Monad в функциональном программировании Мухаммада Зунунова.

  • Чем хороши свободные монады – перевод статьи Габриеллы Гонсалес (Haskell).

• Англоязычные статьи

  • The debatably Free monad подробное последовательное конструирование контейнера Free от Николя Ринаудо.

  • Free Monad in Scala Даниэля Чокырлана с его ресурса Rock the JVM!

  • Free monads - what? and why? Адама Варски.

  • Free Monads Are Simple Ноэля Велша.

• Тип Free[F[_], _] из библиотеки Cats:

  • Free Monad на официальном сайте Type Level;

  • Free monads с ресурса herding cats Юджина Йокоты.

• “Более свободный” контейнер Freer:

  • статья Олега Киселёва и Хироми Ишии Freer Monads, More Extensible Effects;

  • библиотека eff – определённый там трансформер Eff, в отличие от Free из Cats, не требует сборки общего интерпретатора – эффекты “свободной” программы можно интерпретировать последовательно, причём в произвольном порядке;

  • ответ на Stackoverflow Different between Eff monad and Free monad;

  • FreeR - Hybrid Free Monads for Reduced Quadratic Complexity/Observability & Map-Fusion Optimization in Scala - статья в блоге Паскаля Войто;

  • Extensible Effects in Scala – статья из блога Санширо Йошиды (тут вы сможете попрактиковаться в японском языке… или же просто воспользоваться Google-переводчиком).

Продолжения и алгебраические эффекты

В данной статье уже неоднократно упоминалось, что типы целиком определяются отношениями с другими типами, тем, что мы можем сделать, имея данный тип. И для большинства типов важны именно функциональные отношения, возможности использования его значений. Наиболее выразительно эту особенность представляет кодирование Чёрча. Типы в кодировке Чёрча представляют собой способы продолжения вычислений из состояний, характеризуемых значениями этих типов.

Допустим, у нас есть некий тип Type1. Для его значений доступен набор возможностей вида Type1 => A для некоторых типов A. Экзистенциальный характер этого утверждения (“существуют такие типы A, что…“), отражается в следующей универсальной кодировке:

type Type2 = [A] => (Type1 => A) => A

Получаем тип полиморфной функции, принимающей на вход функцию-продолжения вычислений из состояния, в котором известно значение типа Type1. Типы Type1 и Type2 изоморфны: из значений одного типа всегда можно получить значения другого баз потери данных:

val туда:    Type1 => Type2 = (v: Type1) => [A] => (f: Type1 => A) => f(v)
val обратно: Type2 => Type1 = (v: Type2) => v(identity)

assert((туда    andThen обратно)(t1) == t1) // для любых t1: Type1
assert((обратно andThen туда   )(t2) == t2) // для любых t2: Type2

И всё же Type1 и Type2 не эквивалентны – более сложная структура второго даёт больше интересных возможностей.

Функциональные типы, аргументы которых представляют собой другие функции, являются характерной чертой особого стиля передачи продолжений (continuation passing style – CPS). Это типы-контейнеры, для распаковки которых необходимо конкретизировать, как именно будут продолжены вычисления с использованием “хранимого” там значения.

В CPS вызовы продолжений являются хвостовыми. Если язык поддерживает оптимизацию хвостовых вызов (TCO – tail call optimization), то в сочетании с CPS это может дать прирост производительности. В Scala есть оптимизация хвостовой рекурсии (частный случай TCO) и некоторые неочевидные оптимизации для локальных функций.

Полезные CPS-трансформеры для произвольного типа-контейнера, могут иметь весьма нетривиальную структуру. Например, утверждается, что трансформер коплотности для контейнера F[_] изоморфен этому контейнеру:

type Codensity = [F[_]] =>> [A] =>> [B] => (A => F[B]) => F[B]

Для него также определены все необходимые контейнерные возможности:

trait Monad[F[_]]: // важные контейнерные возможности
  val pure:    [A]    => A => F[A]
  val lift:    [A, B] => (A => B) => (F[A] => F[B])
  val flatten: [A]    => F[F[A]] => F[A]
  // map и flatMap строятся из них очевидным образом:
  val map     = [A, B] => (f: A => B) => lift(f)
  val flatMap = [A, B] => (afb: A => F[B]) => (fa: F[A]) => flatten(lift(afb)(fa))
  
given [F[_]]: Monad[Codensity[F]] with
  val pure    = [A]    => (a: A) => [B] => (f: A => F[B]) => f(a)
  val lift    = [A, B] => (ff: A => B) => (coda: Codensity[F][A])  => [C] => (f: B => F[C]) => coda(f compose ff)
  val flatten = [A]    => (codCodA: Codensity[F][Codensity[F][A]]) => [B] => (f: A => F[B]) => codCodA(_ apply f)

Не сложно заметить, что также как и для “более свободного” трансформера Freer, коплотность позволяет строить композицию эффективных вычислений, не накладывая никаких ограничений на исходный контейнер. Но чтобы “поднять” значение из “мира” F[_] в “мир” Codensity[F] всё же потребуются контейнерные возможности для F[_]:

def rep[F[_]: Monad, A](fa: F[A]): Codensity[F][A] = // неявно тянутся возможности Monad[F]
  [B] => (afb: A => F[B]) => summon[Monad[F]].flatMap(afb)(fa) // Monad[F].flatMap

given Monad[Option] with // контейнерные возможности для Option
  val pure =    [A]    => (a: A) => Some(a)
  val lift =    [A, B] => (f: A => B) => (coda: Option[A]) => coda map f
  val flatten = [A]    => (optOptA: Option[Option[A]]) => optOptA.flatten

val codOptInt: Codensity[Option][Int] = rep(Some(42))
val optInt:              Option [Int] = codOptInt(Some.apply) // Some(42)

Таким образом, в отличие от Freer, коплотность не позволяет “освободиться” от контейнерных возможностей F[_]. Однако взамен мы получаем неплохую компенсацию.

Хорошим примером применения коплотности является концепция ресурса, предполагающая следующий цикл вычислений:

В библиотеке Cats есть трансформер Resource, суть которого можно выразить такой конструкцией:

type Resource = [F[_]] =>> [R] =>> (Unit => F[R], R => F[Unit]) => Codensity[F][R]
//                                 (    accure   ,   release  ) => use with continuation

Другими словами, предоставив функции захвата (accure) и освобождения (release) ресурса R, получаем функцию, принимающую на вход функцию-продолжение с реализацией использования (use) ресурса, и возвращающую результат этого использования.

Трансформер Codensity представляет собой полиморфную функцию, что вызывает определённые неудобства при работе с таким типом. Чаще используется тип ContT, представляющий собой такую же функцию, но уже не полиморфную:

type ContT     = [F[_], A, X] =>> (X => F[A]) => F[A]
type Codensity = [F[_]] =>> [X] =>> [A] => ContT[F][A, X]

Трансформер ContT[F, A, X] является контейнером для значений X и его контейнерные возможности также определяются очевидным образом. С типом ContT связана одна очень интересная функция, несколько страшноватого вида:

def callCC[F[_], A, X, Y]
  : ((Y => ContT[F, A, X]) => ContT[F, A, Y]) => ContT[F, A, Y]
  = f => yfa => f { y => _ => yfa(y) }(yfa)
  //                     ↑↑↑↑↑↑↑↑↑↑↑ игорируем переданное продолжение!

Эту функцию “вызова с текущим продолжением” (call with current continuation – callCC) не получится написать для трансформера коплотности. Она позволяет очень гибко управлять потоком вычислений, реализовывать управляющие конструкции, в том числе goto, try/throw/catch/finally, async/await и т.п.

В библиотеке Cats есть своя реализация трансформера ContT, и там уже присутствует метод callCC. На его основе можно построить метод получения текущего продолжения:

def getCC[M[_] : Defer : Monad, R, A]: ContT[M, R, ContT[M, R, A]] = {
  ContT.callCC[M, R, ContT[M, R, A], A] { c =>
    lazy val x: ContT[M, R, A] = ContT.later(c(x).run) // ленивая рекурсия!
    ContT.pure(x)
  }
}

Эту реализацию предложил Матеуш Кубужок (ранее уже упоминались публикации из его замечательного блога), путь к ней он подробно расписал в этом ответе на Stackoverflow. Метод getCC позволяет, например, реализовать ФП-аналог конструкции goto:

def asksLoop =
  for {
    gotoLabel <- getCC[IO, Unit, Unit]
    _         <- ContT.liftF(IO.println("Ходите продолжить? [д/н]"))
    answer    <- ContT.liftF(IO.readLine)
    _ <-      if (answer == "д") gotoLabel
              else               ContT.liftF(IO.unit)
  } yield ()

asksLoop.run(_ => IO.println("Пока!")).unsafeRunSync()

В данном случае можно организовать только “переход назад“, но технически возможны и более сложные сценарии, в том числе, и с передачей состояния.

Так же, по следам другого ответа на Stackoverflow, рассмотрим простой сценарий с использованием callCC для обработки ошибок – будем отслеживать деление на 0.

// вспомогательная функция для удобства
def whenA[F[_], R](b: Boolean)(happyWay: ContT[F, R, Unit]) =
  if (b) happyWay else ContT.pure(())

def div[R](x: Int, y: Int)(handler: String => ContT[IO, R, Int]): ContT[IO, R, Int] =
  ContT.callCC((ok: Int => ContT[IO, R, String]) =>             // "счастливое" продолжение
    ContT.callCC((notOK: String => ContT[IO, R, Unit]) =>       // "несчастливое" продолжение
      whenA(y == 0)(notOK("Нельзя делить на 0 ")) >> ok(x / y)  // выбираем продолжение
    ).flatMap(handler)                                          // обрабатываем "несчастливое" продолжение неизвестным пока методом
  )
val calc1 = div[Unit](10, 2) // : (String => ContT[IO, Unit, Int]) => ContT[IO, Unit, Int]
val calc2 = div[Unit](10, 0) // : (String => ContT[IO, Unit, Int]) => ContT[IO, Unit, Int]

В переменных calc1 и calc2 лежат функции, принимающие на вход строку, а возвращающие… контейнер, для распаковки которого необходимо передать ещё одну функцию-продолжение… Выражения и так не тривиальны, а типы термов в нём ещё сложнее. Но не всё так плохо ? – далее будут упомянуты библиотеки позволяющие использование более простых конструкций, да и сложные типы там не торчат наружу. Пока же посмотрим, как распаковываются подготовленные вычисления. Для этого понадобится обработчик ситуации деления на 0:

def myErrorHandler(str: String) = ContT[IO, Unit, Int]{f => IO.print(str) >> f(42)}
//        не только журналируем, но и ВОССТАНАВЛИВАЕМСЯ с некторым значением ↑↑↑↑↑

// распаковщик вычислений, который и использует обработчик myErrorHandler
def myRun(calc: (String => ContT[IO, Unit, Int]) => ContT[IO, Unit, Int]) = 
  calc
    .apply(myErrorHandler) // применяем обработчик эффекта
    .run(IO.println(_))    // распаковка ContT в IO
    .unsafeRunSync()       // распаковка IO (в Id)

myRun(calc1) // 5
myRun(calc2) // Нельзя делить на 0 42

В комментариях к последним строчкам приведён соответствующий вывод в консоль. Видно, что обработчик ошибок вычислил значение 42 оно вернулось в то место, где была сгенерирована ошибка!

Стиль передачи продолжений позволяет обрабатывать схожим образом не только ошибки, но и любые эффекты. Возможности callCC и передача обработчиков в конце при “распаковке” контейнера подводят к идее алгебраических эффектов. Этот подход позволяет удобно и эффективно комбинировать как стандартные, так и свои абстрактные эффекты, откладывая их интерпретацию на конец программы. В сравнении с свободными контейнерами, когда предварительно требовалось знать перечень всех эффектов для формулировки “тотального” контейнера, концепция алгебраических эффектов не обязывает перечислять все эффекты заранее. Кроме того, основанные на концепции продолжений алгебраические эффекты зачастую обещают выигрыш в производительности.

Для Scala есть несколько библиотек с инструментами для работы с алгебраическими эффектами. Используемые там синтаксические конструкции отличаются друг от друга, поэтому вместо фрагментов кода оставлю ссылки на официальную документацию этих библиотек:

• Scala Effekt (не путать с Cats.Effect) в которой эффекты описываются обычными (не обязательно обобщёнными) трейтами с методами, возвращающими значения в контейнере Control – именно он отвечает за композицию и обработку разных эффектов;

• Turbolift также позволяет работать с абстрактными пользовательскими эффектами, предлагает не самые привычные операторы вроде !! или !@! (?) и гордится высокой производительностью;

• Kyo ориентирован на работу со стандартными эффектами, предоставляет оригинальный синтаксис на основе “стрелок” > и < , и в целом предлагает множество вкусных плюшек.

С алгебраическими эффектами и передачей продолжений связана ещё одна набирающая популярность тема. В англоязычной литературе она называется “Direct Style”, а в русскоязычной… ещё не встречалась ?. Далее будем называть его “императивным стилем”. Давайте посмотрим, ”откуда дует ветер”.

Распространение многозадачных систем и стремление к повышению производительности привела к добавлению в популярные языки программирования специальных синтаксических конструкций, упрощающих асинхронные вычисления. Рассмотрим такой код на C#:

async Task<int> CalcStep1(int v0)
async Task<int> CalcStep2(int v1)

async Task<int> Calc(int v0)
{
	var v1 = await CalcStep1(v0);
	return   await CalcStep2(v1);
}

Связка async/await указывает, что в процессе вычислений, пока операция CalcStep1 ожидает какого-то стороннего сигнала: ответа web-службы и т.п. процессор (точнее, поток, thread) может переключиться на другие вычисления и вернётся к первоначальному, лишь после завершения ожидания. Под капотом этот синтаксический сахар разворачивается в весьма нетривиальный код, который очень упрощённо можно представить так:

Task<int> Calc(int v0)
{
	return CalcStep1(v0)
		.ContinueWith(task1 => CalcStep2(task1.Result), TaskContinuationOptions.OnlyOnRanToCompletion)
		.Unwrap();
}

Метод ContinueWith со вторым параметром TaskContinuationOptions.OnlyOnRanToCompletion похож на знакомый комбинатор map, разве что в принимаемой функции нужно явно вытащить свойство Result у аргумента task1: Task<int>. В свою очередь, метод Unwrap, превращающий Task<Task<int>> в Task<int>, суть не менее знакомый flatten. Вызов ContinueWith в сочетании с Unwrap образуют аналог flatMap. Таким образом, обобщённый C#-тип Task<> является типичным контейнером со всеми ключевыми контейнерными возможностями. Значит async/await – это способ организовать императивную (direct) композицию эффективных вычислений в контейнере!

Также стоит обратить внимание на название метода ContinueWith – явный намёк, что код организован в стиле передачи продолжений. В этом ответе на вопрос на Stackoverflow, демонстрируется, что вызов await CalcStep1(v0) можно символически переписать с помощью (несуществующего в C#) комбинатора callCC как-то так

callCC CalcStep1(v0).GetAwaiter().BeginAwait;

В Cats есть трансформер ContT над любым эффективным контейнером, и даже функция callCC при нём. Значит, должен найтись способ описывать композицию любых эффективных вычислений в императивном стиле, аналогичном использованию async/await в C#. Есть, конечно, for-выражения, но у них слишком много ограничений. Достаточно полноценные решения представлены в виде отдельных библиотек:

• scala-async для контейнера Future;

• cats-effect-cps для IO;

• zio-direct, очевидно, для ZIO (тут используется связка defer/run);

• gears – “доказательство концепции” от авторов Scala 3;

• dotty-cps-async – ещё одна экспериментальная библиотека для Scala 3;

• Monadless с помощью макросов конвертирует обычные императивные вычисления в контейнерные, используя конструкцию lift/unlift;

• Each ещё одна макро-библиотека, но здесь уже работает пара monadic/each;

• Unwrapped библиотека на Scala 3, похоже, что не использует макросы; вместо await там используется bind, а async замещают контекстные функции.

У каждого решения свои особенности, но общая суть. Вот пример по мотивам документации dotty-cps-async:

val c = async[F] {                                     // c: F[String]
  val url     = "http://www.example.com"
  val data    = await(api.fetchUrl(url))               // fetchUrl:         String          => F[String]
  val theme   = api.classifyText(data)                 // classifyText:     String          =>   String
  val dmpInfo = await(api.retrieveDMPInfo(url, theme)) // retrieveDMPInfo: (String, String) => F[String]
  dmpInfo
}

Методы fetchUrl и retrieveDMPInfo возвращают значения в контейнере F и их вызовы обёрнуты в await. Это не распаковка, а некий маркер для макроса async, которой преобразует переданный ему блок в стиле передачи продолжений. Конструкция = await немного напоминает стрелку <- в for-выражении, но никак не ограничивает использование простых императивных операций вроде if, return (ранний выход), или того же for. Более того, поздние версии библиотеки позволяют не писать await, что избавляет от неприятного явления “разноцветных функций”.

Минусы прямого использования стиля передачи продолжений в Scala хорошо сформулировал Матеуш Кубужок. Работа с ContT, Codensity и другими подобными типами сильно напрягают механизм вывод типов Scala, но он всё же слабоват для таких задач, в сравнении, например, с Haskell. То, что в Haskell решается в одну строчку, требует значительных усилий для аналогичных решений в Scala. Также стиль передачи продолжений засоряет стек вызовов, что усложняет отладку кода. Но, с другой стороны, основанные на CPS библиотеки алгебраических эффектов маскируют сложные детали реализации и упрощают стек вызовов, предоставляя очень удобные инструменты для разработки.

Дополнительная литература:

• wiki-сатьи про стиль передачи продолжений:

  • Продолжение (информатика),

  • Haskell/Continuation passing style;

• статьи на Хабре про CPS (смесь русского с хаскелем):

  • Монада ContT в картинках – тут хорошо раскрывается смысл calcCC,

  • Продолжения в Haskell – тут, в частности, рассмотрен пример использования getCC;

• ещё про продолжения:

  • Why would you use ContT? статья Романа Чепляка,

  • when to use CPS vs codensity vs reflection without remorse in Haskell вопрос на Stackoverflow;

• алгебраические эффекты:

  • An Introduction to Algebraic Effects and Handlers pdf-статья Матии Претнара,

  • Effects Without Monads: Non-determinism Back to the Meta Language pdf-статья Олега Киселёва,

  • «Алгебраические эффекты» человеческим языком – хабр-превод статьи Дана Абрамова,

  • хорошую информационную поддержку имеет библиотека Kyo:

    • Kyo - Functional Scala 2023 (презентация),

    • Writing Modular Applications Using The Kyo Library – статья Хорхе Васкеса;

• императивный стиль (direct style):

  • Martin Odersky DIRECT STYLE SCALA – видео-доклад от автора языка,

  • Scala 3: What Is “Direct Style”? – статья Дина Вамплера на Medium.

Tagless Final

Давайте ещё раз рассмотрим контейнер абстрактного эффекта UsersRepo, введённый ранее при рассмотрении свободных контейнеров:

enum UsersRepo[A]:
  case Get(id: UserId)                 extends UsersRepo[Option[UserInfo]]
  case Put(id: UserId, user: UserInfo) extends UsersRepo[UserSaved]
  case ListAll                         extends UsersRepo[List[(UserId, UserInfo)]]

Ранее уже было сказано, что этот обобщённый алгебраический тип (GADT) реализует три функции неявного приведения экземпляров подтипов к значениям в контейнере. Приведение происходят “без потерь“, так как экземпляр типа UsersRepo[A] можно сопоставить с шаблонами-подклассами, и узнать, каким конструктором и из каких значений этот экземпляр создан. По сути, задача подклассов заключается только в хранении исходных параметров.

Экземпляр UsersRepo[A] всегда можно реинтерпретировать в любой другой контейнер. Но вот придумать иной неизоморфный контейнерный тип, который также отражал бы суть рассматриваемого эффекта, и который можно было бы преобразовать к UsersRepo уже не выйдет. То есть, при сохранении семантики такие типы можно лишь усложнить, но сделать проще уже не получится. В этом смысле подобные GADT называют начальными алгебрами соответствующего контейнера.

В свою очередь, интерпретация значений в контейнере UsersRepo, преобразование к другому контейнеру, считается финальным шагом. Разделение вычислений на два шага – начальное построение свободной программы и её финальная интерпретация – ведёт к очевидной потере производительности, что, как правило, не желательно. Если “начальную алгебру” UsersRepo переписать сразу в “финальной” кодировке, использующей, например, контейнер IO, то получится обычный набор функций:

trait UserRepoIO:
  val getUser:   UserId             => IO[Option[UserInfo]]
  val putUser:   UserId => UserInfo => IO[UserSaved]
  val listUsers:                       IO[List[(UserId, UserInfo)]]

Самый обычный ООП-шный трейт UserRepoIO представляет собой финальную кодировку, соответствующую начальной алгебре UsersRepo. Основное его преимущество заключается в том, что вычисление происходит быстрее, в один шаг. Недостатком в сравнении с начальной алгеброй является избыточная жёсткость – хотя и можно предоставить различную реализацию этих методов, но в их сигнатуре уже вшит тип контейнера, что ограничивает интерпретацию.

Можно ли используя финальную кодировку с её “скоростью” получить “свободу интерпретации”, присущую начальной кодировке? Давайте попробуем заменить IO в UserRepoIO на некий контейнер F:

trait UserRepoF[F[_]]: // некий неизвестный контейнер F
  val getUser:   UserId             => F[Option[UserInfo]]
  val putUser:   UserId => UserInfo => F[UserSaved]
  val listUsers:                       F[List[(UserId, UserInfo)]]

Внезапно, это и есть искомое решение! В то время как разработка на основе свободных контейнеров, помогала абстрагироваться от конкретных эффектов, техника Tagless Final позволяет абстрагироваться от контейнера, носителя контекста эффекта. Рассмотрим пару примеров реализации этого трейта (интерпретации алгебры UserRepoF):

type Log[X] = String // константный контейнер
val log = new UserRepoF[Log]:
  val getUser   = id         => s"Получить пользователя с идентификатором $id"
  val putUser   = id => user => s"Сохранить пользователя $user под идентификатором $id"
  val listUsers =                "Перечислить всех пользователей"

В подобной интерпретации каждый метод теперь может вернуть значения любого нужного типа; в случае контейнера Log, это String. А вот так можно получить и начальную алгебру:

import UsersRepo.*
val usersRepoAlg = new UserRepoF[UsersRepo]:
  val getUser   = Get.apply
  val putUser   = Put.apply.curried
  val listUsers = ListAll

Обобщённые трейты вроде UserRepoF, параметризированные обобщённым же ковариантным типом-контейнером F[_], представляют собой легко узнаваемую основу техники Scala-разработки, известную под названием Tagless Final. Слово “final” в названии соответствует использованию финальной кодировки. “Tagless” же отсылает к древнему злу ко временам, когда типизацию приходилось блюсти вручную, сверяя во время выполнения “теги” – дополнительные метаданные, передаваемые вместе с целевыми значениями. Появление в программировании обобщённых типов перенесло соответствующие механизмы типизации на этап компиляции, что позволило перейти к “бестеговой” (tagless) разработке.

Если с основой Tagless Final более или менее познакомились, осталось разобраться, как комбинировать вычисления с использованием конечного кодирования. Будем трактовать обобщённый трейт UserRepoF как класс контейнерных типов. Значения UserRepoF[SomeF] для конкретного SomeF содержат реализации соответствующих возможностей для этого контейнера. Ситуация аналогична привязке “контейнерных возможностей” к произвольным обобщённым (ковариантным) типам вида , когда также используются классы типов. Таким образом, при построении Tagless Final программы требуются экземпляры классов типов как всех используемых финальных алгебр

trait SearchServcieF[F[_]]:
  def searchBest   (request: String): F[Data]
  def searchSeveral(request: String): F[List[(Relevance, Data)]]

trait NotificationServiceF[F[_]]:
  def sendNotification(notification: Notification): F[NotificationResult]

так и “контейнерных”, вроде Monad из библиотеки Cats, позволяющего, в частности, использовать методы map и flatMap:

import cats.Monad
import cats.syntax.all.*

def programTF[F[_]: UserRepoF: SearchServcieF: NotificationServiceF: Monad]: F[List[(Relevance, Data)]] =
  val userRepo = summon[UserRepoF[F]]
  import userRepo.*

  val searchService = summon[SearchServcieF[F]]
  import searchService.*

  val notificationService = summon[NotificationServiceF[F]]
  import notificationService.*

  // далее уже знакомый код
  searchBest("best user")           productL
  sendNotification("user captured") flatMap
  putUser(42)                       productR
  getUser(42)                       map
  {_.fold("")(_.reverse)}           flatMap
  putUser(24)                       productR
  listUsers

Чтобы избавиться от “мусорных” призывов и импортов в теле programTF рекомендуется описать дополнительный DSL для конечных алгебр:

object UserRepoF:
  def getUser  [F[_]: UserRepoF] = summon[UserRepoF[F]].getUser
  def putUser  [F[_]: UserRepoF] = summon[UserRepoF[F]].putUser
  def listUsers[F[_]: UserRepoF] = summon[UserRepoF[F]].listUsers

object SearchServcieF:
  def searchBest   [F[_]: SearchServcieF] = summon[SearchServcieF[F]].searchBest
  def searchSeveral[F[_]: SearchServcieF] = summon[SearchServcieF[F]].searchSeveral

object NotificationServiceF:
  def sendNotification[F[_]: NotificationServiceF] = summon[NotificationServiceF[F]].sendNotification

В итоге получаем в точности такое же тело программы, как и в примере для свободных контейнеров, но уже в финальной кодировке:

import UserRepoF.*, SearchServcieF.*, NotificationServiceF.*

def programTF[F[_]: UserRepoF: SearchServcieF: NotificationServiceF: Monad] =
  searchBest("best user")           productL
  sendNotification("user captured") flatMap
  putUser(42)                       productR
  getUser(42)                       map
  {_.fold("")(_.reverse)}           flatMap
  putUser(24)                       productR
  listUsers

Для выполнения программы необходимо в контекст положить неявные значения финальных алгебр, конкретизированных выбранным контейнером (сами реализации не принципиальны):

given UserRepoF[IO] with
  override val getUser   = ???
  override val putUser   = ???
  override val listUsers = ???

given SearchServcieF[IO] with
  override val searchBest    = ???
  override val searchSeveral = ???

given NotificationServiceF[IO] with
  override val sendNotification = ???

Алгебра Monad[IO] уже реализована в объекте-компаньоне контейнера IO и импортируется автоматически. Теперь осталось только выполнить программу:

programTF[IO] // : IO[List[(UserId, UserInfo)]]

Функция programTF, в свою очередь, также может быть реализацией метода некоторой алгебры, более высокоуровневой с точки зрения предметной области. Это означает, что с Tagless Final очевидным образом можно строить и многослойные приложения.

Техника Tagless Final хорошо сочетается с экосистемой Cats, библиотеки которой содержат как стандартные “контейнерные” классы типов, так и базовые эффекты вроде обработки ошибок, или асинхронщины. Библиотека Cats-tagless предлагает набор макро-аннотаций для конечных алгебр, которые позволяют сократить объём шаблонного кода, и добавляют другие вкусные плюшки. Контейнеры ZIO также можно использовать с конечными алгебрами, но эта экосистема старается дистанцироваться от Tagless Final, говоря, что для ZIO-разработки это всё не нужно.

Tagless Final даёт хорошую иллюстрацию использования типов высокого рода. Будучи основанной на контейнерных типах вида , она оперирует типами-алгебрами вида . А в статье Луки Якубовича Optimizing Tagless Final – saying farewell to Free демонстрируется преобразование программ, построенных на конечных алгебрах – полиморфные типы таких программ имеют ещё более сложный вид .

Как и в случае свободных контейнеров, техника Tagless Final позволяет по-разному интерпретировать сконструированные программы, что может быть удобно, когда возможны миграции на другие контейнеры эффектов, или же когда для тестирования удобно использовать более простые контейнеры. Но благодаря своей “финальности” Tagless Final избавляет от лишнего шага построения во время выполнения начальной алгебры программы.

Говоря же о недостатках данной техники, обычно отсылают к статье “The False Hope of Managing Effects With Tagless-Final in Scala” автора библиотеки ZIO Джона де Гуса. Да, там заметно стремление продвинуть свой продукт, конкурирующий с экосистемой Cats, но можно найти вполне резонные замечания. Во-первых, даже для абстрактных для контейнеров очень важны “контейнерные возможности”, так что при реализации финальных алгебр почти повсеместно приходится писать что-то вроде F[_]: Monad – код уже теряет некоторую долю выразительности. То же замечание относится и к некоторым другим классам типов, отвечающим за “популярные“ эффекты (например, Async[F[_]]). Но более важно то, что усложнение кода для “свободы интерпретации” навряд ли может быть оправдано требованиями бизнеса – в большинстве приложений, финальные алгебры реализуются для единственного контейнера (чаще всего, это IO из библиотеки Cats).

Дополнительная литература:

• Tagless Final in Scala – хороший обзор от Даниэля Чокырлана (Rock the JVM).

• A "quick" introduction to Tagless Final – ещё одно чуть более современное “введение” Николя Ринаудо.

• Хабр-статья Возвращаясь к Неразмеченным Конечным Интерпретаторам с Dotty.

• теоретическая PDF-статья Finally Tagless, Partially Evaluated.

Клейсли и другие стре́лки

Императивный стиль, о котором говорилось ранее, позволяет “чисто” описывать эффективные программы в привычной старинной манере, основанной на использовании стека. При таком подходе вычисления разбиваются на шаги, переводящие одно состояние стека в другое. Эти состояния можно визуализировать в виде кортежей из инициализированных локальных переменных:

К сожалению, слишком редко говорят о том, что такое программирование чревато букетом принципиальных проблем:

• количество инициированных переменных растёт с каждым шагом, при этом, использованные переменные “устаревают”, засоряя контекст:

  • как следствие, очень легко перепутать последовательность шагов (например, сделать лишние действия до проверки их надобности), или же

  • вместо нужной использовать “устаревшую“ переменную того же типа и т.п.;

• компьютеры и компиляторы умнеют, но мы по-прежнему относимся к ним как к “дурочкам”, многословно объясняя, куда положить вычисленное значение и как потом его использовать;

  • требуются дополнительные (необязательные!) синтаксические конструкции, вроде инициализации локальных переменных,

  • страдает выразительность кода, что, статистически, приводит к просачиванию ошибок на этап исполнения. С такой точки зрения само стремление разработчиков к традиционному императивному стилю выглядит как поиск привычных граблей для натренированной мозоли на лбу.

В качестве альтернативы императивному стилю можно выбрать потоковый синтаксис (flow syntax), при котором подразумевается, что состояния между шагами описываются единственной переменной:

def calc(b: Boolean) = b
  .toString
  .length
  .+(37) // оператор "+" - это самый обычный метод в Scala

calc(false) // 42

В данном примере потоковый синтаксис основан на вызове через точку . собственных методов классов, или методов расширения. Но аналогичным образом можно композировать и обычные функции:

def boolToString(b: Boolean) = b.toString
def stringToInt (s: String)  = s.length
def add37       (i: Int)     = i + 37

import scala.util.chaining.scalaUtilChainingOps

def calc(b: Boolean) =
  b            pipe
  boolToString pipe
  stringToInt  pipe
  add37

Комбинатор pipe – полиморфный метод-расширение, импортированный из scalaUtilChainingOps и записанный в инфиксной операторной форме. Он просто передаёт левый аргумент в функцию, указанную справа (в нашем случае, на следующей строке). Кстати, похожая запись уже встречалась для контейнерных вычислений, где вместо pipe использовался комбинатор flatMap.

Уже лучше, но мы всё ещё не избавились от императивности окончательно. На каждом шаге вычислений в calc у нас остаётся соблазн использовать “устаревшую”, но по-прежнему доступную, переменную b, переданную в функцию как аргумент. Можно ли устранить и эту проблему? Конечно, если писать всё сразу в функциональном стиле, когда сложные функции представляются в виде комбинации простых:

val calc = // : Boolean => Int - тип выводится автоматически
  boolToString andThen
  stringToInt  andThen
  add37
  
calc(false) // 42

Комбинатор andThen здесь – встроенный метод класса Function1. Итоговая функция есть “boolToString, затем stringToInt, затем add37”. Максимально идеоматично, ничего лишнего! Мы полностью избавились от состояний, следовательно, нет и необходимости в трассировке calc, тут просто нечему ломаться! Такой стиль называется “бесточечным”. Под “точками” в теории категорий подразумевают промежуточные состояния, значения локальных переменных в стеке.

Также есть дуальный метод compose, действующий аналогично andThen, но в обратном направлении. Запись val calc = add37 compose stringToInt compose boolToString можно прочесть как “функция calc – это результат вычисления add37 после stringToInt, после boolToString”.

В случае контейнерных вычислений нужно комбинировать функции вида A => F[B]. Для таких функций библиотека Cats предлагает комбинаторы andThenF и composeF, доступные, только если для F[_] реализован класс типов FlatMap[F[_]] с необходимыми контейнерными возможностями.

Также библиотека Cats предлагает синонимы таких комбинаторов в виде стрелочек-операторов: >>>, >=> и <<<, <=<. Например:

val stringToIntOpt: String => Option[Int] = _.toIntOption
val devideOpt:         Int => Option[Int] =
  i => if (42 % i == 0) Some(42 / i) else None

import cats.syntax.all.*
val calc = devideOpt <=< stringToIntOpt
//                   ↑↑↑ оператор ?
calc("7") // Some(6)

Cемантика последовательной композиции вычислений доступна не только для типов простых и “эффективных” функций. Общий вид этих типов будет таким:

type ==>[-_, +_]

По сути, ==> и есть абстрактная “стрелка”. Но типы, как это было и с контейнерами, определяются через свои возможности. В частности, стрелки также определяются реализацией соответствующего класса типов. Стрелки обладают внушительным количеством базовых возможностей, которые можно собрать из следующих классов:

type Identity   [==>[-_, +_]] = [A] => () => (A ==> A)
type AndThen    [==>[-_, +_]] = [A, B, C] => (A ==> B, B ==> C) => (A ==> C)
type Category   [==>[-_, +_]] = Identity[==>] & AndThen[==>]

type Dimap      [==>[-_, +_]] = [A, B, C, D] => (C => A, B => D) => (A ==> B) => (C ==> D)
type First      [==>[-_, +_]] = [A, B, C] => (A ==> B) => ((A, C) ==> (B, C)) // технически, можно
type Second     [==>[-_, +_]] = [A, B, C] => (A ==> B) => ((C, A) ==> (C, B)) // обойтись только одним
type Strong     [==>[-_, +_]] = Dimap[==>] & First[==>] & Second[==>]

type Arr        [==>[-_, +_]] = [A, B] => (A => B) => (A ==> B)
type Arrow      [==>[-_, +_]] = Category[==>] & Strong[==>] & Arr[==>]

type Choose     [==>[-_, +_]] = [A, B, C, D] => ((A ==> C), (B ==> D)) => ((A Either B) ==> (C Either D))
type ArrowChoice[==>[-_, +_]] = Arrow[==>] & Choose[==>]

Для этих классов типов вводятся следующие удобные функции:

def ident[==>[-_, +_] : Identity] = summon[Identity[==>]]()

extension[==>[-_, +_]: Dimap, A, B] (fab: A ==> B)
  def dimap[C, D](ca: C => A, bd: B => D) = summon[Dimap[==>]](ca, bd)(fab)

extension[==>[-_, +_]: AndThen, A, B] (fab: A ==> B)
  def andThen[C](fbc: B ==> C) = summon[AndThen[==>]](fab, fbc)
  def >>>    [C](fbc: B ==> C) = fab andThen fbc  
  def compose[C](fca: C ==> A) = fca andThen fab
  def <<<    [C](fca: C ==> A) = fab compose fca

extension[==>[-_, +_]: First, A, B] (fab: A ==> B)
  def first[C]  = summon[First [==>]][A, B, C](fab)
extension[==>[-_, +_]: Second, A, B] (fab: A ==> B)
  def second[C] = summon[Second[==>]][A, B, C](fab)

extension[A, B] (fab: A => B)
  def arr[==>[-_, +_]: Arr] = summon[Arr[==>]](fab)

extension[==>[-_, +_]: Arrow, A, B] (fab: A ==> B)
  def split[C, D](fcd: C ==> D) = fab.first andThen fcd.second
  def ***  [C, D](fcd: C ==> D) = fab split fcd
  def merge[C   ](fac: A ==> C) = ((a: A) => (a, a)).arr[==>] andThen (fab split fac)
  def &&&  [C   ](fac: A ==> C) = fab merge fac

extension[==>[-_, +_]: Choose, A, C] (fac: A ==> C)
  def choose[B, D](fbd: B ==> D) = summon[Choose[==>]](fac, fbd)
  def +++   [B, D](fbd: B ==> D) = fac choose fbd

extension[==>[-_, +_]: ArrowChoice, A, C] (fac: A ==> C)
  def choice[B](fbd: B ==> C) = (fac +++ fbd).dimap(identity[A Either B], _.fold(identity, identity))
  def |||   [B](fbd: B ==> C) = fac choice fbd

Возможностей у стрелок больше чем у контейнерных типов, но в коде выше многие функции дублированы своими синонимами в виде символических операторов. Именно они наиболее интересны: >>>, <<<, &&&, ***, +++.

Посмотрим как использовать эти операторы для стрелок из библиотеки Cats. Там реализованы неявные значения класса Arrow для обычных функций, а также для типов Kleisli и Cokleisli, которые изоморфны таким конструкциям:

type Function [       -A, +B] =   A  =>   B  // небольшой каламбур ?
type Kleisli  [F[+_], -A, +B] =   A  => F[B] // синонимичен ReaderT
type Cokleisli[F[+_], -A, +B] = F[A] =>   B  // тоже местами интересен, но тут не будет о нём

Будем строить программу как большую эффективную стрелку типа Kleisli[IO, *, *] на основе следующих кирпичиков:

import cats.effect.IO
import cats.data.Kleisli
import cats.syntax.all.*

type ==>[A, B] = Kleisli[IO, A, B]

val boolToString :  Boolean    ==> String = Kleisli{ b     => b.toString.pure}
val getFirstChar :  String     ==> Char   = Kleisli{ s     => IO{s.head}}
val stringToInt  :  String     ==> Int    = Kleisli{ s     => IO{s.length}}
val replicateChar: (Char, Int) ==> String = Kleisli{(c, i) => (c.toString * i).pure}

Сама же эффективная программа записывается в полностью бесточечном стиле:

val program = boolToString >>> (getFirstChar &&& stringToInt) >>> replicateChar
//  program : Boolean ==> String

import cats.effect.unsafe.implicits.global
program(true).unsafeRunSync() // tttt

(Неужели кто-то всё ещё хочет развивать императивный стиль в Scala?)

Стрелки ковариантны по второму параметру, следовательно, они также относятся к контейнерам и для них реализуются все необходимые возможности. Но на самом деле он гораздо богаче. Ранее говорилось, что классы типов Applicative и Monad ориентированы на, соответственно, независимое (параллельное) и последовательное выполнение эффектов. Стрелки же допускают оба способа комбинирования вычислений.

Стрелки не исчерпываются только лишь отображениями из одного контейнера в другой, вида F[A] => G[B]. На сайте документации Cats приводится пример рекурсивной стрелки FancyFunction. Или другой пример:

type InverseFunction[-A, +B] = (B => A) => (A => B)

Хоть и не очень понятно, как можно использовать эту “инвертированную функцию”, но для неё тоже реализуются основные стрелочные возможности.

Стрелки, также как и контейнеры могут быть “свободными”. Инструменты для построения программ на их основе предоставляются, например, библиотекой Free Arrow. Операции бизнес-логики описываются в виде привычных алгебраических типов данных, но параметризированных уже двумя типами. Далее они “поднимаются” до “свободных стрелок”, из которых уже строится цепочка вычислений. Для получения результата необходимо предоставить “интерпретатор” – преобразователь из наших абстрактных стрелок во что-то вычислимое, например, в тот же Kleisli. Другими словами, достаточно пройти тот же самый путь, что и со свободным контейнерами, но получить более широкие возможности стрелок при построении программы.

Не смотря на то, что стрелки значительно богаче контейнеров, построение решений на самописных стрелках оказывается слишком громоздким для повседневного использования. Обычно рекомендуют стоить программы только на основе контейнеров (в том числе и с Kleisli над ними), и только там, где они не справляются, допускается использование самодельных стрелок. Тем не менее, всё это не отменяет очевидный факт:

Стрелки отражают саму суть функционального программирования.

Дополнительные источники по стрелкам:

• Стрелки в популярных Scala-библиотеках:

  • Arrow на официальном сайте о Cats от TypeLevel.

  • Arrow из библиотеки Cats с ресурса herding cats Юджина Йокоты.

  • Arrow из библиотеки Scalaz с того ресурса learning Scalaz того же автора.

  • ZIO Arrow (без комментариев).

• Стрелки в Scala

  • Рефакторинг при помощи композиции Клейсли – хабр-статья, в которой используется Kleisli из библиотеки Scalaz.

  • Composing Monadic Functions with Kleisli Arrows статья Санджива Сахаяма.

  • Functional Programming with Arrows презентация Юрия Полюли.

  • Arrows, Monads and Kleisli – статья в двух частях на Medium от Марцина Ржежницкого.

• Стрелки в Haskell:

  • Understanding arrows подробная статья с картинками.

  • [Monads vs. Arrows](https://stackoverflow.com/questions/3652054/monads- vs-arrows) вопрос на Stackoverflow.

Подкатегории типов (вместо заключения)

Процесс вычислений разбивается на этапы, последовательно превращающие начальное состояние в конечное. Например, этап-функция принимает на вход начальное состояние-значение, возвращает промежуточное, которое передаётся на вход следующему этапу-функции, и так далее до финального состояния-значения. Функции выстраиваются в цепочку, образуя путь вычислений. Это можно визуализировать в виде линейного графа:

Но, как уже говорилось ранее, не все вычисления производятся на уровне значений. Простые конструкторы типов описывают превращения одних типов в другие. Но обобщённые типы и сами могут выступать в качестве точек-состояний для полиморфных типов более высокого рода. Кроме того, в статье уже упоминались “путешествия” между вселенными типов, когда, например, из точки-значения можно прийти к точке-типу, или наоборот. На самом деле, есть и более интересные совокупности точек и переходов между ними, которые хоть и не очень явно, но также используются в программировании. И чтобы представить полный путь вычислений нужна более общая концепция, чем значения и их типы.

Такая концепция называется категорией. Абстрактная категория представляет собой как раз совокупность неких точек-объектов и стрелок-морфизмов между ними. При этом для категории есть обязательные условия: существование ассоциативной композиции морфизмов , и наличие у каждого объекта единичного морфизма , переводящего объект в самого себя:

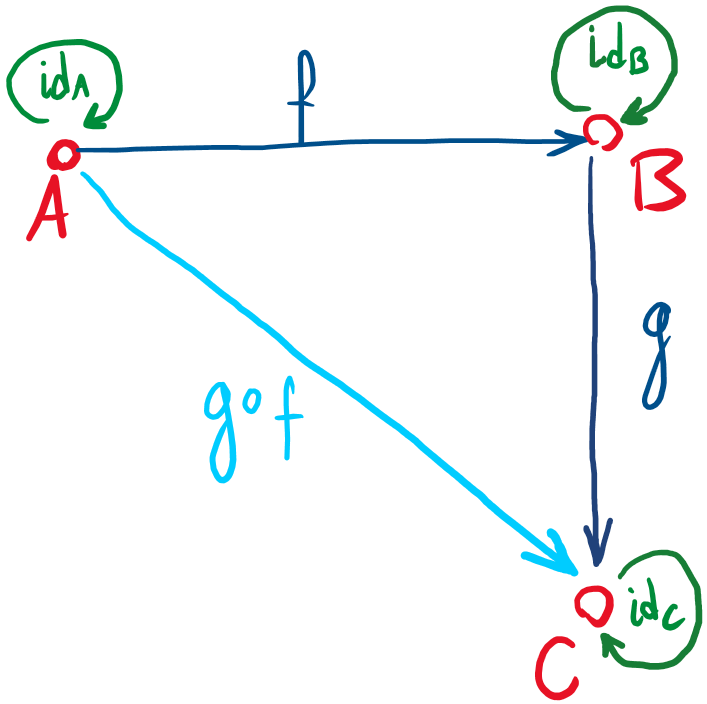
Такая банальная, на первый взгляд, конструкция позволяет оперировать уже не только стрелками-морфизмами на графе, но целыми путями, построенными из этих стрелок – сравнивать их между собой и выбирать наилучший.

Очевидно, что свои категории образуют значения, типы, конструкторы типов, виды типов и много чего ещё. Например, конструктор типов Either[A, B] переводит пару типов в тип. Но пары типов сами по себе типами не является – они образуют собственную категорию! А Either представляет собой морфизм из категории пар типов в категорию типов. Напрашивается интуиция, что совокупность категорий сама образует категорию.

В контексте обобщённых типов нам, прежде всего, важно то, что категории могут содержать вложенные подкатегории. В категории, объектами которой являются типы, а морфизмами – функции A => B, каждый обобщённый тип F[_] образует свою подкатегорию типов с морфизмами-функциями F[A] => F[B]. И это даёт очередную интерпретацию обобщённых типов.

Практически все понятия, введённые в статье, так или иначе опираются на теорию категорий:

• все простые обобщённые типы являются морфизмами вида в категории типов;

• каждый обобщённый тип F[_] представляют собой подкатегорию типов ;

• аналогичные рассуждения можно провести для полиморфных типов любого вида (например, и др.);

• вселенные типов образуют категорию с морфизмами-путешествиями между ними;

• класс контейнерных типов Lift[F[_]] (с возможностью map) олицетворяет эндофунктор из категорией типов в её подкатегорию: ;

• волнистая стрелка ~>[F[_], G[_]] представляет собой вообще говоря, функтор между подкатегориями F и G, но удобнее считать, что это естественное преобразование между эндофункторами и , направленными из категории типов в неё же (потому и приставка “эндо-”, "внутренний");

• в частности, класс типов Flatten[F[_]] совместно с Pure[F[_]] и Lift[F[_]] представляют такую пару естественных преобразований (pure и flatten) для эндофункторов, которая относится к понятию монада;

• возможность перестановки контейнеров местами F[G[A]] => G[F[A]], в том числе, когда один из них кортеж (Applicative), определяется тем, как именно функторы и сопряжены друг с другом: или ;

• свободный контейнер Free[F[_]] ассоциируется с начальным (свободным) объектом в категории монад над функтором – свободным моноидом в категории эндофункторов;

• трансформер коплотности Codensity[F[_]] представляет собой правое расширение Кана функтора вдоль самого себя: ;

• стрелки же описывают (сильные) профункторы – функторы в категорию множеств из декартова произведения категорий , где есть категория, дуальная типам (объекты – те же типы, что и в исходной категории, но все морфизмы-функции направлены в противоположную сторону).

Пожалуй, одного только этого списка должно быть достаточно для демонстрации фундаментальности теории категорий. Но всё же, что дают все эти высокоуровневые абстракции обычным программистам?

Теория категория зародилась как раздел топологии с целью предоставить достаточно выразительный язык как для описания уже существовавших там понятий, так и для формулирования новых. Один из классов задач топологии связан с операциями над путями между двумя точками – вычисления отношений между ними и т.п. К этому классу относится, например, нахождение кратчайшего пути на ориентированном графе между заданными точками. Но ведь именно это и требуется программистам – с помощью всех доступных возможностей найти наилучший путь вычисления нужного результата!

Теория категория как раз предоставляет удобный инструментарий для работы с путями вычислений. Многие понятия (функторы, монады и т.п.) определяются в ней через коммутирование диаграмм – различные пути на этих диаграммах приводят к одинаковому результату, что позволяет выбрать из них наиболее подходящий. Но, пожалуй, интереснее всего те понятия, которые определяются через своё “универсальное свойство”, утверждающее “избранность“ какого-то морфизма среди аналогичных. Именно универсальные свойства различных конструкций указывают наикратчайший путь вычислений.

Теория категорий объясняет, почему именно те, а не иные конструкции являются наилучшими инструментами при разработке компьютерных программ.

Упомянутый ранее императивный стиль (direct style) показывает, что сложные вычисления можно “замести под ковёр”, оставив на поверхности лишь нужные синтаксические конструкции. Но надо помнить, что любая такая надстройка стоит на универсальном фундаменте теории категорий.

В данной статье часто упоминается Scala-библиотека с забавным названием Cats. Ресурс Юджина Йокоты herding cats со статьями об использовании этой библиотеки с первой страницы отсылает к шуточному рекламному ролику (отсылающему к известной идиоме). Но всё же, в первую очередь, название берёт начало от “теории категорий” (Categories). Реализованные в библиотеке инструменты бывают очень полезны в работе не только с контейнером IO, но и с ZIO, Future, не говоря уже об обычных Option, List и т.п.

Также в данной статье постоянно используется термин “контейнер” везде, где обычно говорят о “монадах” или “функторах”. Такое решение выбрано здесь потому, что использовать такие термины теории категорий по отношению, например, к Option[_], вообще говоря, некорректно. Также функторами и монадами не являются одноименные классы типов – это именно что “классы”, к которым, для того же Option, относятся конкретные значения типов Functor[Option], Moand[Option]. И только эти значения (кои могут иметь разные реализации для одного и того же конструктора типов!) правильно называть функторами и монадами. Для обобщённых же типов будет точнее использовать термин подкатегории типов. Причём, это относится не только к ковариантным контейнерам, но и контравариантным обобщённым типам – такую подкатегорию будут связывать с исходной уже контравариантные функторы.

Более детальный обзор теории категорий в приложении к программированию ожидается в одной из следующих статей. Здесь же пока предложу ознакомиться с такими материалами:

• хабр-переводы (см. ссылки в начале и саму статью) первых глав книги “Теория категорий для программистов” Бартоша Милевски;

• Теория категорий на JavaScript. Часть 1. Категория множеств – тут хорошие картинки, раскрывающие, в частности, понятие “универсального свойства”;

• Монады с точки зрения программистов (и немного теории категорий) – примеры на Hakell, но также есть несколько наглядных иллюстраций;

Ещё порекомендую книгу Сергея Виницкого The Science of Functional Programming – это версия 2021 года, а более свежую версию можно самому приобрести, или попробовать собрать из исходников на GitHub.

Итак, мы рассмотрели, на первый взгляд, простое понятие “обобщённые типы” с самых разных ракурсов. Кроме того, прояснили, как они помогают создавать простые, эффективные и надёжные программы. Надеюсь, этот обзор оказался полезен читателю не меньше, чем и автору ?.