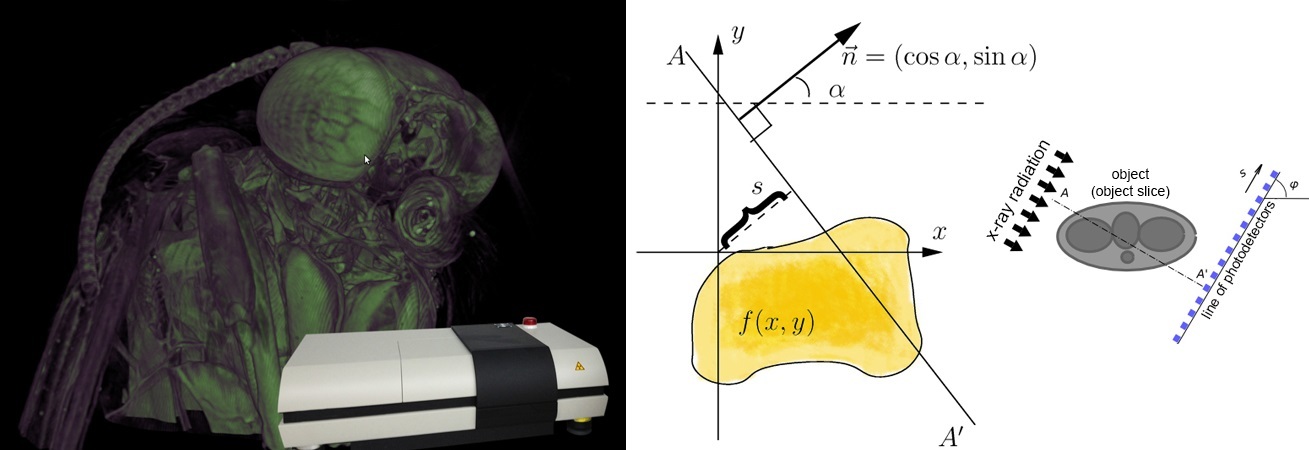
Хочу поподробнее рассказать об интересном проекте компании Edison. Перед разработчиками поставили задачу написать софт для микротомографа, они с этим отлично справились, а потом запихивали в этот томограф семечки, болты, конденсаторы и моль. А серьезным дядям этот томограф нужен, чтобы проверять алмазы и не покупать дырявые.

А еще сегодня 16 декабря, день рождения Иоганна Радона, австрийского математика, ректора Венского университета, который в 1917 году ввел интегральное преобразование функции многих переменных, родственное преобразованию Фурье, используемое сегодня во всех томографах.

Иоганн Радон был профессором 6 университетов (а в одном из них даже без кафедры), был президентом Австрийского математического общества. В Австрии в честь него назвали «Институт вычислительной и прикладной математики» и медаль.

О том, как проходила разработка софта для томографа и какие задачи решались в процессе — под катом.

Микротомограф

Ученые из томского государственного университета создали микротомограф. Он позволяет с точностью до микрона узнать о внутренней структуре различных материалов. Например, алмазов.





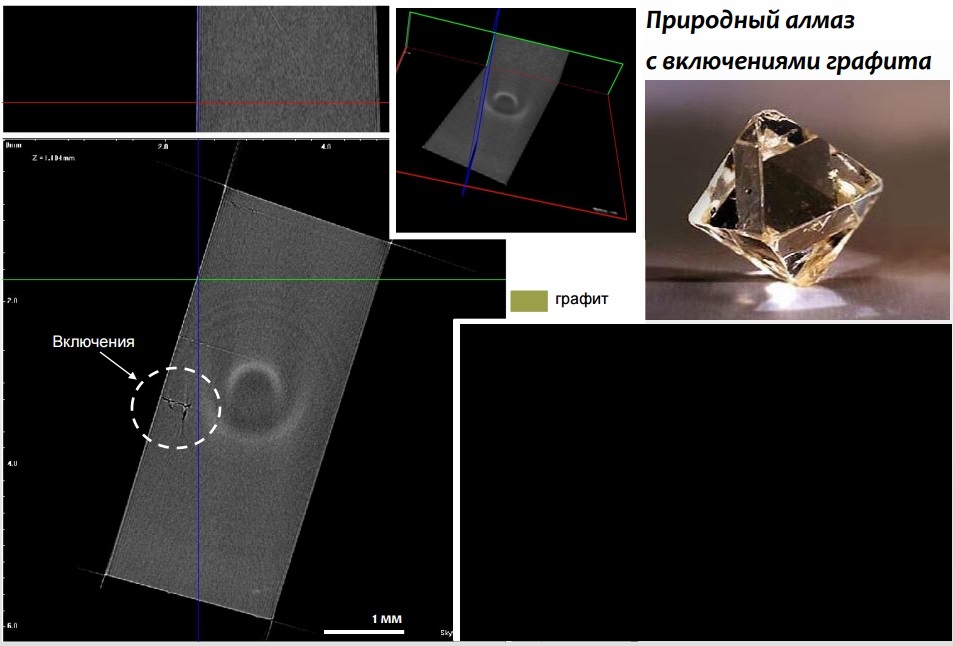
Томограф может просветить материал с разрешением до микрона. Это в 100 раз тоньше человеческого волоса. После сканирования программа создает 3D-модель, где можно посмотреть не только на внешнюю сторону детали, но и узнать, что у нее внутри.





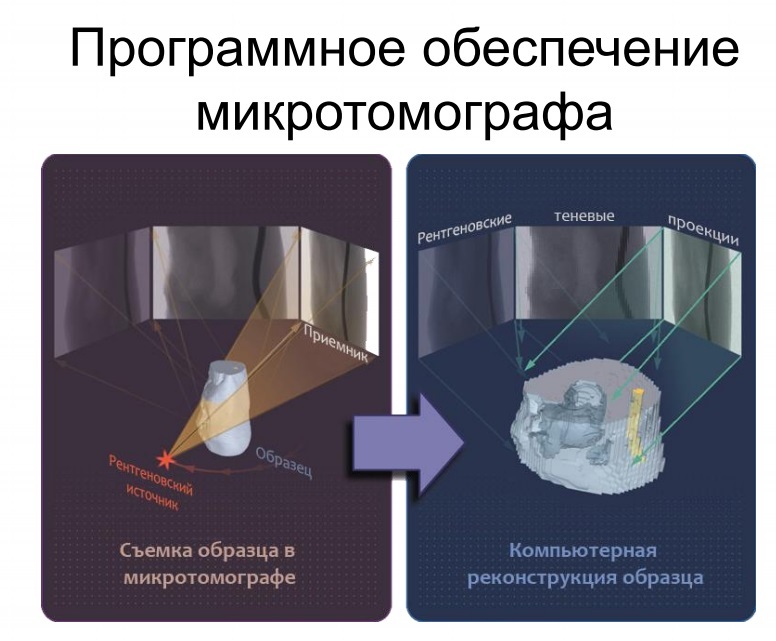
Используемые математические алгоритмы.

• Обратное преобразование Радона.
• Марширующие/шагающие кубы.
• Фильтр Гаусса.
• Фильтрация/свертка, нормализация проекций.

Реализация и технологии.

• C++/Qt.
• Ubuntu, Windows.
• CUDA.
• Объемный-воксельный рендеринг модели.
• Собственный формат хранения изображений с оттенками серого глубиной 12 бит.
• Разделение реконструкции на клиент-сервер.
• Сохранение объемных данных в виде «Октодеревьев».

Трудозатраты: 5233 человеко-часа.
Отладка производилась на сырых данных (проекционных снимках), полученных с томографа.

Алгоритмы

В первую очередь, необходимо было подобрать математический аппарат для решения задачи. Основной алгоритм — обратное преобразование Радона — был заложен в постановку задачи,

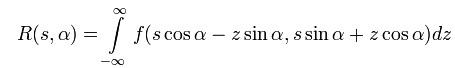
однако его потребовалось адаптировать под особенности нашей работы и использовать несколько дополнительных, вспомогательных алгоритмов. Например, ввиду того, что объект просвечивался одной «лампочкой», пришлось адаптировать формулы обратного преобразования Радона под конические, а не прямые проекции. Стандартный алгоритм подразумевает, что объект просвечивается пучком параллельных рентгеновских лучей, исходящих от бесконечно удалённого источника. В реальности источник лучей точечный, поэтому и пучок лучей имеет форму конуса. В связи с этим в алгоритм обратного преобразования Радона потребовалось ввести преобразование координат из конической системы в прямоугольную.

На первой стадии вычислений производится предварительная фильтрация/свертка, нормализация проекций. Это необходимо для того, чтобы на проекциях приглушить шумы, а плотности более явно выделить.

Для построения 3D-моделей поверхностей объектов в стандартном формате для просмотра в 3D-редакторах Компас, SolidWork, 3D Max Studio использовался алгоритм «Марширующие (шагающие) кубы». Суть алгоритма в том, что он пробегает скалярное поле, на каждой итерации просматривает 8 соседних позиций (вершины куба, параллельного осям координат) и определяет полигоны, необходимые для представления части изоповерхности, проходящей через данный куб. Далее, на экран выводятся полигоны, образующие заданную изоповерхность.

Под фильтром Гаусса в проекте понимается матричный фильтры обработки изображений с использованием матрицы свертки. Матрица свёртки – это матрица коэффициентов, которая «умножается» на значение пикселей изображения для получения требуемого результата. Фильтр используется для сглаживания воксельных данных и проекций срезов, что, в свою очередь, позволяет улучшить качество генерируемых 3D-моделей (Хабрапост 1, Хабрапост 2).

Реализация и технологии

В ходе работы также был создан ряд специализированных технических решений: библиотека для объемно-воксельного рендеринга модели; запись видео при выполнении операций с моделью; собственный формат хранения изображений с оттенками серого глубиной 12 бит; сохранение объемных данных в виде «Октодеревьев»; алгоритмы полигонизации 3D-модели.


Объемный-воксельный рендеринг модели в проекте использовался для просмотра модели с возможностью вращения и масштабирования в реальном времени. Воксель — это трехмерный пиксель. Так же с помощью воксельного рендеринга оператору предоставляются удобные инструменты для определения области просмотра с автоматическим увеличением уровня детализации и возможность расположения секущей плоскости под любым углом в два клика. На основе секущей плоскости в дальнейшем можно получить изображение среза с максимальным разрешением.
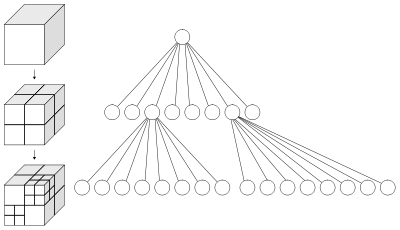Октодерево (дерево октантов, восьмеричное дерево, англ. octree) — тип древовидной структуры данных, в которой у каждого внутреннего узла ровно восемь «потомков». Восьмеричные деревья чаще всего используются для разделения трёхмерного пространства, рекурсивно разделяя его на восемь ячеек. В проекте октодерево позволяет выполнять отображение данных в режиме предварительного просмотра, когда нет необходимости в данных, которые не видны пользователю. Так, например, объемный рендеринг получает набор данных для отображения с детализацией в зависимости от выбранной области с помощью октодерева, что обеспечивает высокий FPS, когда видна вся модель, и в то же время увеличение детализации, если выбрана какая-то меньшая часть модели.

Отладка

Далее следовал этап оптимизации. Для одного объекта томограф выдаёт 360 снимков, каждый разрешением до 8000*8000. Поскольку объём обрабатываемых данных велик, решение задачи «в лоб» было бы совершенно неудовлетворительно. Это учитывалось ещё на этапе проектирования, однако после получения первой версии алгоритмы пришлось несколько раз оптимизировать и адаптировать. Задание требовало, чтобы время создания трехмерной модели микроструктуры не превышало более 2-х часов, поэтому этап оптимизации был заложен изначально. В ходе тестирования первой версии мы столкнулись с тем, что использование стандартного формата хранения изображений проекций не подходит для проекта. Входные данные содержат изображения формата TIFF с 16-битным кодированием оттенков серого. Такая глубина цвета для расчётов избыточна, а дискового пространства, сетевого канала, оперативной памяти и процессорного времени обработка таких изображений требует много. С другой стороны, стандартной 8-битной глубины цвета нам оказалось недостаточно для сохранения точности реконструкции. Поэтому был разработан формат хранения изображений с 12-битной глубиной цвета.

В технический проект было заложено горизонтальное масштабирование вычислений. Реконструкция 3D-модели, то есть основная вычислительная задача, разделялась на небольшие пакеты-задания, которые центральный модуль ПО распределял по сети серверов в кластере. На серверах применялась технология CUDA, позволяющая задействовать вычислительные мощности графических процессоров для расчётов. Время, требуемое для расчёта одной модели, сокращается пропорционально количеству серверов в кластере, так как вычислительные задачи идеально распараллеливаются, и все серверы загружены на 100%.



Архитектура CUDA применима не только для высокопроизводительных графических вычислений, но и для различных научных вычислений с использованием видеокарт nVidia. Ученые и исследователи широко используют CUDA в различных областях, включая астрофизику, вычислительную биологию и химию, моделирование динамики жидкостей, электромагнитных взаимодействий, компьютерную томографию, сейсмический анализ и многое другое. В CUDA имеется возможность подключения к приложениям, использующим OpenGL и Direct3D. CUDA — кроссплатформенное программное обеспечение для таких операционных систем как Linux, Mac OS X и Windows.

В нашем проекте CUDA применяется для основного процесса — реконструкции объёмных данных из проекций. Так как графические процессоры имеют специализированный набор команд, то вычисления реконструкции хорошо ложились именно на графические карты через технологию CUDA. На CPU данная задача решается дольше как на этапе разработки, так и на этапе выполнения.


Карты, поддерживаемые нашим ПО:

• Nvidia Tesla K80 24GB (научная);
• EVGA GeForce GTX TITAN X 12GB (игровая).

Задание предусматривало, что ПО должно работать в среде Microsoft Windows XP/Vista/7, Linux. В связи с этим кроссплатформенность решения была заложена изначально. В качестве языка разработки был выбран C++/Qt, что позволило иметь единый исходный код и собирать ПО под разные ОС.

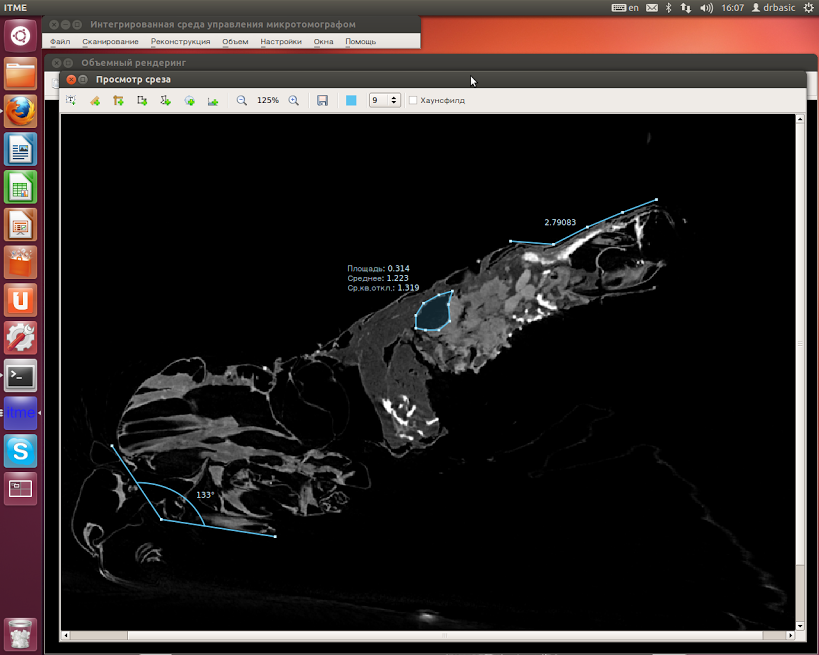
Видео