
Группа бразильских ученых опубликовала исследование, посвященное созданию инструмента для предсказания поведения активов, торгующихся на фондовом рынке. В работе представлено подробное описание метода и способа расчетов для подобных прогнозов. Мы представляем вашему вниманию наиболее интересные моменты этого документа.
Что такое адаптивный фильтр
Адаптивный фильтр — это инструмент, способный к самообучению для достижения заданного уровня соответсвия выходных данных реальному положению вещей. Под адаптивностью понимается возможность реагировать на изменения входных данных в режиме реального времени для достижения более высокой производительности. На практике, адаптивные алгоритмы реализуются двумя классическими методами — методом градиента и наименьших квадратов (LMS и RLS). Подобный фильтр может быть использован для широкого спектра задач — фильтрации, спектрального анализа или поиска сигналов и т.д.
На рисунке 1 представлена универсальная схема применения адаптивного фильтра в предиктивном фреймворке, где k — это номер итерации, x(k ) — входящий сигнал, y(k) — вывод адаптивного фильтра, являющийся прогнозом желаемого ответа d(k), а e(k) — сигнал ошибки, определяемый как разница между желаемым ответом и выводом фильтра, то есть e(k) = d(k) — y(k).
Рекурсивный адаптивный алгоритм наименьших квадратов (RLS, recursive Least-Squares) позволяет добиваться высокой производительности и скорости сходимости при использовании в переменных во времени средах.
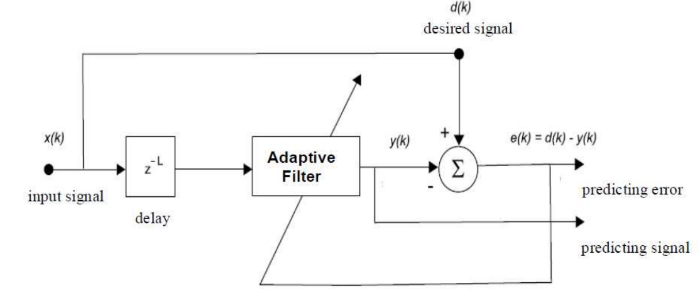
Рис. 1. Общая блок-диаграмма адаптивного фильтра для предсказания сигналов
Еще один важный параметр — это так называемое окно наблюдений, то есть временной период анализа, который обычно имеет прямоугольное или экспоненциальное соответствие. Параметр, контролирующий соответствие и длительность окна наблюдений называется коэффициентов забывания
? (он применяется к памяти алгоритма), 0 << ? < 1 и объектная функция выглядит так: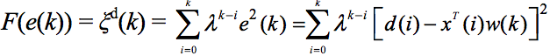
Эта функция выпукла в многомерном пространстве
w(k), то есть ?d(k) имеет лишь один глобальный минимум и ни одного локального минимума. Таким образом, мы можем достичь этой точки, установив градиент ?d(k) равным нулю, что приведет к такой формуле: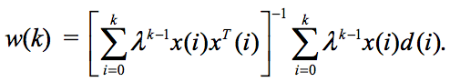
Использование адаптивного фильтра в фреймворке предсказаний цен акций
Цель данного исследования — понять, насколько жизнеспособен вариант с использованием адаптивной фильтрации в качестве инструмента для предсказания цен акций на реальных биржах. Адаптивный LMS-фильтр успешно применялся для предсказания трафика в беспроводных сетях [Liang (2002)]. В текущем случае адаптивная фильтрация использовалась для получения оценки возможной стоимости акций акций компании Petrobras, торгующихся на бразильской бирже Bovespa в Сан-Паулу (тикер PETR3).
Для создания модуля предсказания движения цены PETR3 был использован адаптивный цифровой FIR-фильтр со 100 реальными коэффициентами. В качестве алгоритма адаптации был использован RLS с коэффициентом забывания 0,98. Также было использовано окно предсказуемости размером в 16 дней. Симуляция производилась на платформе MATLAB, в качестве входных данных использовалась торговая информация в период с 01/03/2000 до 09/23/2009. Значения дневных цен акций соответствуют моменту закрытия торгов. На рисунке 2 показана сходимость коэффициентов адаптивного фильтра, использующегося в ходе создания предсказаний движения цены PETR3.
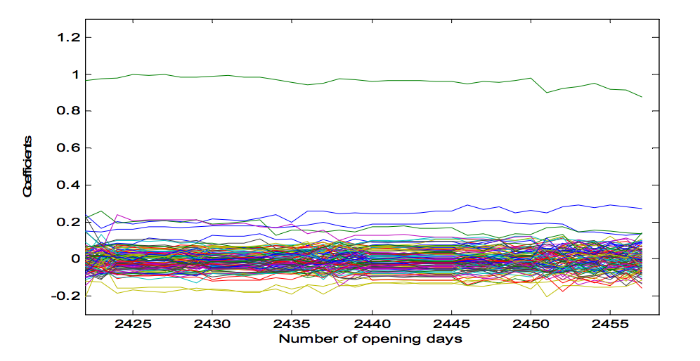
Рис. 2. Сходимость коэффициентов адаптивного фильтра, запущенного для генерирования предсказаний цен акций компании Petrobras (PETR3 на бразильском фондовом рынке).
Эволюция коэффициентов фильтрации ясно демонстрирует наличие сходимости в период, примерно совпадающий со временем предсказания. По оси абсцисс отмечено число торговых дней, участвующих в симуляции. Реальная оценка акций PETR3 на бразильском фондовом рынке в указанный период показана красной линией на рисунке 3. Там же черным отмечены значения предсказанных фильтром цен.
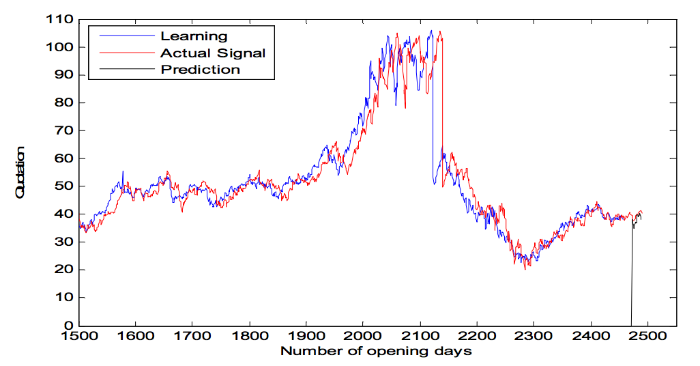
Рис. 3. Цена акций PETR3 на бразильском фондовом рынке в период анализа для фильтрации. Красным показан реальный рыночный тренд, черным — оценка, сгенерированная адаптивным фильтром.
Очевидно, что существует соответствие предсказанных цен и тем, как дела обстояли на рынке в действительности. Для подтверждения этого факта было проведено моделирование конкретного торгового дня — конкретно 2,450 день с начала наблюдений 1/3/2000 года. На рисунке 4 показан зум предсказания, сделанного адаптивным фильтром:
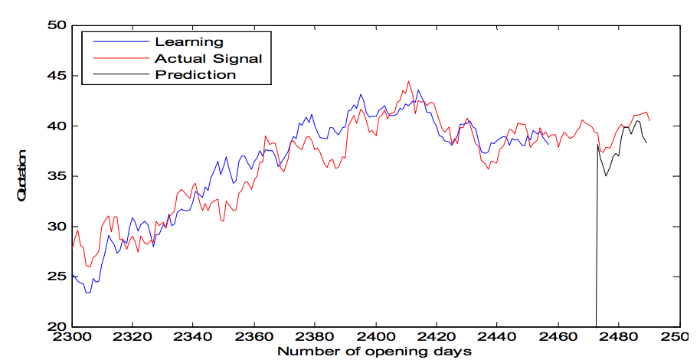
Рис. 4. Предсказание цен акций в конкретный день
Производительность адаптивного фильтра для предсказания цен выбранного актива
Рассмотрим стратегии инвестиций в акции PETR3 с использованием предсказаний, сгенерированных фильтром с момента 2473 (показан на рис. 5). Фильтрация осуществляется с помощью RLS-алгоритма с 100 коэффициентами и коэффициентом забывания ? = 0,98. Предполагаемый тренд движения цен акций PETR3 на основе фильтрации для 16-дневного окна отображен пунктирной линией на рисунке 5.
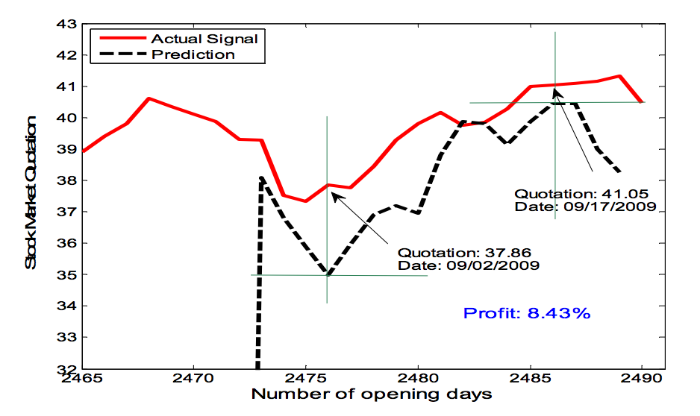
Рис. 5. Поведение актива PETR3 в период с 08/18/2009 до 09/22/2009. Пунктир — предсказание адаптивного фильтра, красным — реальная цена акций на рынке.
Кривая предсказания говорит о необходимости покупки актива в торговый день 09/02/2009 и продажи акций в момент 17/09/2009 — таким образом продажа должна прийтись на момент роста, предшествующего снижению цен. График реальных цен говорит о том, что если бы такая стратегия была реализована, то покупка акций прошла бы по цене 37,86, а продажа по 41,05, что дало бы прибыль в размере 8,43% от объёма инвестиций. Несмотря на то, что данный пример является лишь частным случаем, он иллюстрирует возможную эффективность предсказаний, основанных на адаптивной фильтрации. В дальнейшем были проведены испытания для других торговых дней, и результаты в общем были такими же.
Создание адаптивного фильтра и точность предсказаний
Несмотря на положительные результаты испытаний, предложенный метод оставляет некоторые вопросы. Один из них звучит так — для какого типа активов он работает лучше? Какое количество коэффициентов FIR следует использовать для повышения качества работы модуля предсказания? Влият ли на результат значение коэффициента забывания?
Для оценки качества предсказаний, сделанных с помощью адаптивной фильтрации, используется корреляция — это мера схожести для анализа качества совпадения между предсказанным сигналом и реальными котировками на бирже в рамках заданного окна предсказания.
Анализ точности осуществляется с помощью изучения значений корреляции, как функции числа коэффициентов фильтра и размером окна предсказания. На рисунке 5 показан 3D-график корреляции между 08/18/2009 и 09/22/2009:
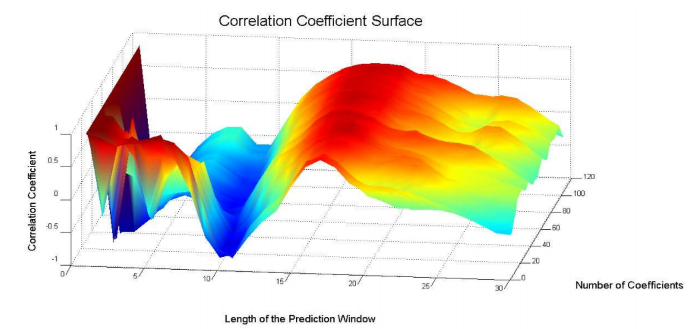
Рис. 6. Корреляционный 3D-график между предсказанными сигналами и реальными котировками акций.
График 6 был конвертирован в трехмерный контурный график, представленный на рисунке 7. На нем лучше видна зона повышенной корреляции между сгенерированным предсказанным сигналом и реальными ценами акций на рынке.

Для изучения влияние числа коэффициентов фильтра для адаптивных предсказаний был создан боковой профиль пространства из рисунка 6 (изображен на рис. 8), на котором отмечены пики корреляции, видимые наблюдателю, находящемуся в правой части пространства. Очевидно, что участок между 30 и 100 коэффициентами представляет высокую корреляцию. Соответственно, использование 30 и меньшего числа коэффциентов недостаточно для получения точного предсказания.
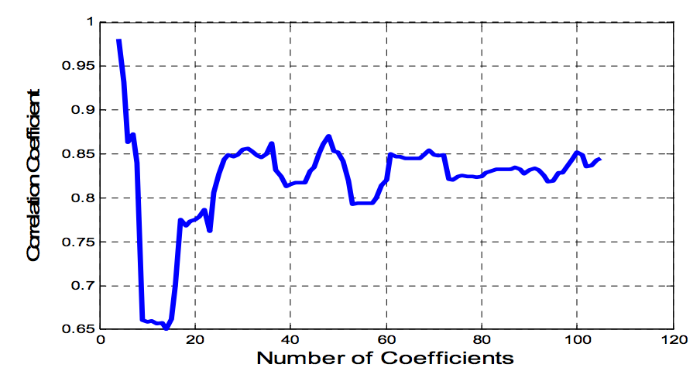
Рис. 8. Профиль корреляции, учитывающий число коэффициентов.
Первый участок высокой корреляции не особенно полезен, поскольку его можно достигнуть только при очень маленьком окне предсказания. Наилучшим вариантом в данном конкретном сценарии является выбор числа коэффициентов между 60 и 100.
Затем для оценки влияния окна предсказания на качество получаемых прогнозов, был создан передний профиль трехмерного пространства из рисунка 6 (рис. 9). На нем показано поведение максимальной корреляции с учетом размеров окна предсказания. Очевидно, что выбор очень короткого окна ведет к высокой корреляции (действительно, цены акций идущих друг за другом торговых дней показывают высокую корреляцию). Однако это практически ничего не дает нам в плане создания стратегий инвестирования на фондовом рынке.
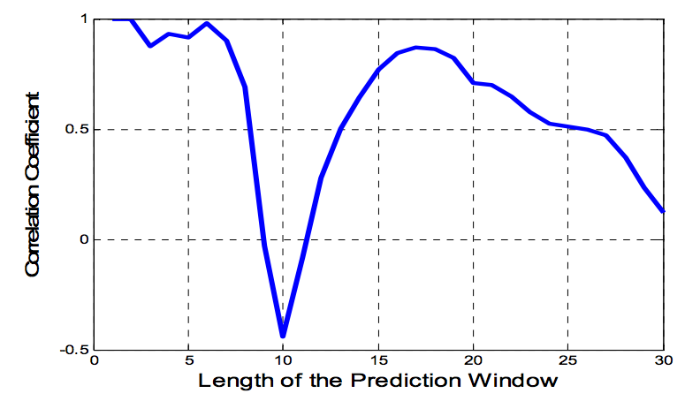
Рис. 9. Профиль корреляции с учетом размером окна предсказания (от 1 до 30 торговых дней бразильского фондового рынка).
Неожиданный результат — эксперименты показали, что выбор окна предсказания размером около 10 дней является крайне неэффективным. Напротив, предсказания на окне в примерно 15 рабочих дней показывают гораздо лучшие результаты. Точно также, как и предполагалось, слишком длинные окна предсказания приводят к снижению коррелюяции.
Таким образом, наиболее оптимальным окном предсказания в данном конкретном случае является 15-20 дней.
В таблице 1 представлена сводная информация о количестве использованных коэффициентов, длине окна предсказания, даты покупки и продажи акций согласно предложенной фильтром стратегии, цены сделок, а также общий профит транзакций.
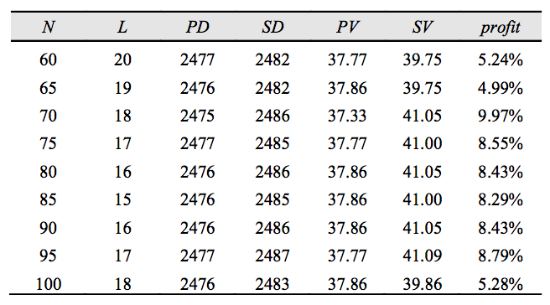
Как видно, использование адаптивного фильтра позволило добиться получения прибыли, в среднем, в размере 7% от объёма инвестиций.
Комментарии (3)

sergehog
11.01.2016 15:19+2LMS ассимптотически стремится к Moore-Penrose pseudo-inverse, который кстати так и называется Least-Squares Solution. Так что для большей «точности» можно уж сразу его использовать, просто построить большую матрицу из всех известных данных и вперед. Современные методы позволяют инвертировать огромные матрицы достаточно быстро, так что скорость не проблема, тем более если бабки нужны :)
Но вообще то аппроксимация рыночной конъюктуры линейной моделью от предыдущих данных это что то совсем тупое. Я хоть и не спец в этой области, но интуиция подсказывает что это никогда не сработает на реальных данных. Может надо какой-нибудь kernel-method приделать чтоб хотя-бы нелинейную модель получить. Да и то навряд ли.


u1d
>позволило добиться получения прибыли, в среднем, в размере 7%
Сильный вывод.
Похоже, что это они по одной сделке такой вывод сделали, сгенерировав ее с разными вариантами длины окна прогнозирования и N и усреднив полученные результаты, в текущем виде никакой стат. значимости в этой «средней» прибыли 7%. А как в остальные периоды (кроме этих рассмотренных 20 дней) их предиктор работает им было лениво считать что ли?)
ProLimit
Так это как раз самый ключевой момент исследвания, но про него очень скромно описано в одну строчку «В дальнейшем были проведены испытания для других торговых дней, и результаты в общем были такими же.». Понимай как хочешь. Похоже на манипулирование путем сокрытия части информации — в статье явно не хватает примеров, где фильтр ошибся, и соотношение ошибок и успехов на длительном периоде.