Однако в приложениях наряду с последовательностями случайных и псевдослучайных чисел требуется получать перестановки чисел, имеющие равномерное распределение. Например, потребность в таких перестановках периодически появляется в криптографических приложениях.
Метод описанный ниже предложен Санделиусом (М. Sandelius) еще в 1962 г. в работе [1].
Описываемый алгоритм позволяет получать случайные перестановки из n элементов, которые имеют равномерное распределение. Последнее означает, что вероятность получить одну из n! возможных подстановок, используя данный метод равна 1/n!..
Алгоритм получения перестановок
Метод Санделиуса проще описать рекурсивно.
На каждом шаге обрабатывается массив P. Для массива P генерируются случайные биты в количестве равном числу элементов в массиве P. i-тый бит последовательности сопоставляется i-тому элементу массива P. Массив P делится на два массива P0 и P1 по принципу: все элементы, которым сопоставлены нули заносятся в массив P0, остальные в массив P1. Для каждого массива P0 и P1 выполняется перемешивание (рекурсия). Перемешанные массивы объединяются в один. Сначала идут элементы из массива P0, затем из массива P1.
Процедура перемешивания Sandelius(P):
1. n := |P|; - мощность (число элементов) P
2. Если n=1, то вернуть P;
3. g:=[gi, i=1..n]; – получение последовательности случайных бит gi
4. P0:=[]; P1:=[]; - пустые массивы
5. i0:=0; i1:=0; - индексы для записи в массивы
6. k:= 0;
7. Если g[k]=0, то
7.1. P0[i0] := P[k];
7.2. i0 := i0+1;
8. Если g[k]=1, то
8.1. P1[i1] := P[k];
8.2. i1 := i1+1;
9. k := k+1;
10. Если k<n, то переходим к шагу 7.
11. P0 := Sandelius(P0);
12. P1 := Sandelius(P1);
13. P := P0||P1 – объединяем массивы в один большой массив.
14. Возвращаем P.
Перестановка по методу Санделиуса получается из последовательности чисел от 1 до n:
P=[1,2, …,n];
Sandelius(P);
Алгоритм, довольно легко программируется.
Sandelius:=proc(p)
local A,m,i,p1,p2;
m:=nops(p);
A:=[seq(getNextRndBit(), i=1..m)];
p1:=[]; p2:=[];
for i from 1 to m do
if A[i]=0 then p1:=[op(p1),p[i]];
else p2:=[op(p2),p[i]];
fi;
od;
if nops(p1)>1 then p1:=Sandelius(p1); fi;
if nops(p2)>1 then p2:=Sandelius(p2); fi;
return [op(p1),op(p2)];
end proc:
unsigned __int8 *bits,*tmp_perm;
Sandelius(unsigned __int8 *perm,int n)
{
tmp_perm = (unsigned __int8 *)malloc(n);
bits = (unsigned __int8 *)malloc(n);
for(int i=0;i<n;i++) perm[i]=i;
recursiveSandelius(perm,n);
free(bits);
free(tmp_perm);
}
recursiveSandelius(unsigned __int8 *perm,int n)
{
if (n<=1) return;
for(int i=0;i<n;i++)
bits[i]=getNextRndBit();
k=0;
for(int i=0;i<n;i++)
if(!bits[i])
tmp_perm[k++]=perm[i];
zeros=k;
for(int i=0;i<n;i++)
if(bits[i])
tmp_perm[k++]=perm[i];
memcpy(perm,tmp_perm,n);
recursiveSandelius (perm,zeros);
recursiveSandelius (&perm[zeros],n-zeros);
}
Особенности
Надеюсь, алгоритм генерации перестановки описан мною достаточно понятно. Теперь хочется немного обсудить, особенности его работы.
Для работы алгоритм требует последовательность случайных бит. Главное требование к этой последовательности – биты должны быть независимыми. В этом случае алгоритм генерирует равномерно распределенные перестановки даже.
Следует учитывать, что случайные биты могут иметь неравномерное распределение, но они должны быть независимыми, иначе распределение подстановок не будет равномерным.
К недостаткам можно отнести тот факт, что число случайных бит, которые потребуются для генерации перестановки не определено заранее.
Практическая проверка
Сразу скажу, что факты указанные в предыдущем пункте доказываются аналитически, но все равно захотелось проверить их на практике.
Для проверки равномерности распределения получаемых подстановок написана простая программа в математическом пакете Maple. В программе я генерировал большое число перестановок, подсчитывал количество подстановок каждого вида (что-то вроде гистограммы). Для полученного массива проверялась гипотеза о равномерности по критерию Пирсона. Кроме того, подсчитывалось распределение количества бит, требуемых для генерации одной подстановки.
Приводить исходный текст программы здесь не вижу смысла, но если есть желание посчитать самим, то файлы с исходными кодами можно найти тут.
Исследовались перестановки длины n=7. Генерировалось N=n!*1000 перестановок. Случайные биты генерировались так: 0 с вероятностью 0,5+d, 1 с вероятностью 0,5-d. d равно 0 для равномерно распределенных бит. Для получения зависимого бита генерировался случайный бит и складывался с предыдущим битом.
Число n=7 взято из соображений разумного времени выполнения (у меня это 10-20 минут).
| Вариант | Равновероятные подстановки (критерий Пирсона)? | Гистограмма | Среднее число случайных бит/среднеквадратичное отклонение |
|---|---|---|---|
| Независимые биты, d=0 | Да | 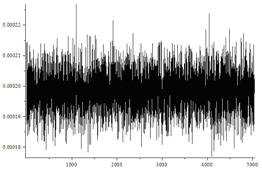 |
28.24/28.26 |
| Независимые биты, d=0.05 | Да | 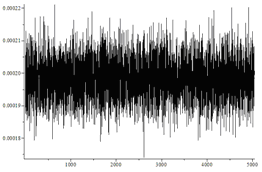 |
28.50/28,54 |
| Независимые биты, d=0.4 | Да | 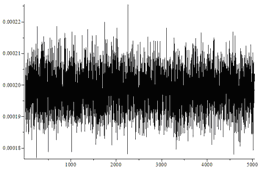 |
71.47/74.77 |
| Зависимые биты, d=0.05 | Нет | 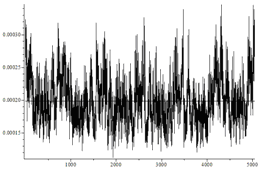 |
30.15/30.32 |
На рисунках по горизонтали отмечены номера перестановок, а по вертикали частоты их появления. Не вооруженным глазом видно, что в последнем случае распределение сильно отличается от равномерного.
Так же видно, что не зависимо от перекоса в вероятности независимых случайных бит алгоритм генерирует равномерно распределенные перестановки. Однако чем больше перекос в вероятности, тем больше случайных бит требует алгоритм.
Если же биты имеют зависимость, то генерируемые подстановки имеют распределение отличное от равномерного распределения.
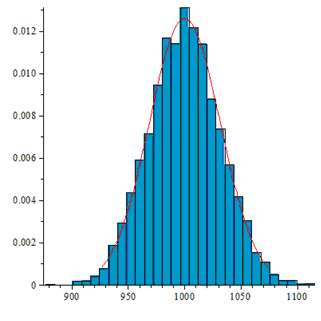
Количество подстановок, каждого типа должно иметь распределение близкое к нормальному со средним N/n! и дисперсией N/n!(1-1/n!).
В первых трех случаях гистограмма выглядит примерно так:
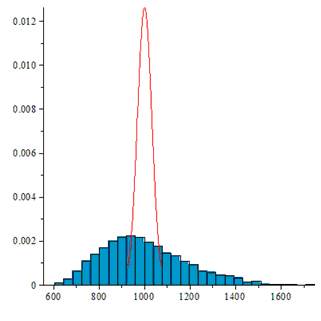
В последнем случае видно, распределение далеко от ожидаемого:
Литература
1. М. Sandelius. A Simple Randomisation Procedure, J. of the Royal Statistical Society. Ser. В., V. 24, № 2, 1962.
Комментарии (19)

mihaild
22.01.2016 23:23Кажется надо явно написать в начале, что мы учитываем возможность разной вероятности 0 и 1. Потому что если она одинаковая, то можно, например, просто сгенерировать случайное число от 0 до n!..

vasiatka
23.01.2016 11:59С ростом n для вам будут нужны все более длинные числа с равномерным распределением в заданном диапазоне…
n=256 около 1700 бит
n=512 около 3900 бит
n=1024 около 8800 бит
n=2048 около 19600 бит
В каждом случае вам потребуется гарантировать (доказывать) независимость и равномерность распределения. этих чисел.
И если мне не изменяет память, чтобы номер преобразовать в подстановку вам потребуется делить длинные числа и находить остатки от деления длинных чисел.
А так, наверное, проблем больше не будет…
mihaild
23.01.2016 12:21+3Да, нам нужны всё более длинные числа, но в любом случае нужно не меньше чем log_2(n!) бит энтропии.
Вопрос качества источника случайности — отдельный. Указанный вами способ тоже требует независимости отдельных бит)
(но да, он работает для любой вероятности 0/1)

MichaelBorisov
23.01.2016 01:12+3Изучая код функции randperm в Matlab, я обнаружил следующий алгоритм.
1) Генерируем равномерно распределенные случайные числа (например, в диапазоне 0..1) для каждого элемента последовательности, для которой мы хотим получить случайную перестановку.
2) Сортируем полученные случайные числа по неубыванию, запоминая при этом индексы оригинальной последовательности случайных чисел. В результате получается последовательность индексов.
3) Размещаем элементы исходной последовательности в соответствии с индексами, полученными на шаге 2).
В матлаб-коде это выглядит так:
function b = randperm(a) % The function accepts a vector a and returns its random permutation as b x = rand(size(a)); % Generate a random number vector with the same size as a [xs,i] = sort(x); % Sort the random numbers, store indices such that xs = x(i), see help sort b = a(i); % Use the same indices to permute the original vector a
Преимущество метода — заранее известно требуемое кол-во случайных чисел. В зависимости от используемого метода сортировки заранее известна сложность (максимальная или средняя, в случае qsort)
Если требуется получить перестановку не произвольных элементов, а последовательности натуральных чисел длиной n — то можно сразу возвращать массив индексов.
Вопросы:
1) Для описанного выше метода, гарантируется ли равномерное распределение перестановок?
2) Если оно гарантируется — какой метод эффективнее, описанный выше или приведенный в статье?
mihaild
23.01.2016 12:23+31) да, гарантируется
2) ваш метод существенно сложнее (требует генерации чисел на отрезке)
Если мы можем использовать достаточно сильные генераторы (например, генерировать равномерно числа на отрезке) — то мы можем генерировать и равномерно числа из 1,2,...,n — и использовать метод Кнута.
vasiatka
23.01.2016 13:33Может я что-то путаю… Есть несколько вариантов тасования Кнута, в том числе и с сортировкой.

vasiatka
23.01.2016 13:28+11) Генерируем равномерно распределенные случайные числа (например, в диапазоне 0..1) для каждого элемента последовательности, для которой мы хотим получить случайную перестановку.
В вашем случае, числами 0 и 1 не обойдешся. Rand должен давать случайные числа из диапазона шириной существенно большей числа элементов перестановки.
Предложенный метод, сильно напоминает тасование Кнута (вариант с сортировкой). У оригинального алгоритма Кнута (Фишера–Йетса) асимптотика O(n).
Асимптотическая оценка скорости сортировки в лучшем случае равна O(n log n), что несравнимо с оценкой O(n) скорости работы оригинального тасования Кнута. Cортирующий метод дает несмещенные перестановки, но он менее чувствителен к возможным проблемам генератора случайных чисел. Однако следует уделить особое внимание генерации случайных чисел, чтобы избежать повторения, поскольку алгоритм с сортировкой, в общем случае, не сортирует элементы случайно.
1. Если rand генерирует равномерно распределенные числа, то перестановки, полученные им, также будут иметь равномерное распределение. Думаю, если сделать проверку аналогичную той, что делал я в статье, то перестановки сгенерируются с равномерным распределением.
Про гарантированное распределение, тут все определяется качеством чисел, которые выдает rand.
2. Возможно, предложенный Санделиусом алгоритм и не самый быстрый, но не такой требовательный к качеству входной последовательности (смотрите в табличке третью строку там вероятность появления нулей 0,9, но перестановки все равно получаются равномерно распределенными).
mihaild
24.01.2016 00:57+1Строго говоря, алгоритмов, генерирующих случайную перестановку быстрее, чем за O(NlogN) не бывает по той же причине, что и не бывает таких алгоритмов сортировки.

kreep
23.01.2016 18:21+1Насколько я понимаю, этот метод работает в среднем за O(N logN), где N — число элементов перестановки. В то время как алгоритм Фишера-Йетса работает за O(N), да и пишется куда проще.
Я буду читать комментарии

lgorSL
24.01.2016 00:26+1В примере на С++ можно было бы не использовать дополнительную память.
Если я правильно понимаю, функция выдаёт независимые биты, и потому не важно, в каком порядке мы их спрашиваем. Можно по аналогии с qSort идти от начала, запрашивая рандомные биты, пока не наткнёмся на 1, а потом двигаться с конца, пока не получим 0.

nickolaym
25.01.2016 14:40Правильно я понимаю, что алгоритм не гарантирует остановку?
Допустим, ГСЧ заклинило, и он начал выдавать «совершенно случайно» только нули или только единицы.
Тогда рекурсивный алгоритм будет жрать время и стек до посинения.
Или, допустим, ГСЧ решил выдавать такую последовательность:
1 ноль, n-1 единиц
1 единица, n-2 нулей
1 ноль, n-3 единиц…
в среднем-то нулей и единиц поровну… Ну да, в белом шуме попалась «любимая мелодия».
А время работы из линейного или логлинейного превратилось в квадратичное!
mihaild
25.01.2016 16:53Ну, если PRG зажилил энтропию и не отдает — то тут уж ничего сделать нельзя (либо выдать фиксированный ответ, либо зависнуть).

nickolaym
25.01.2016 20:08А чего это он зажилил?
Может, первые десять лет аптайма ГСЧ выдавал чересчур белый шум, и вот прямо сейчас пришла пора в течение суток выдавать сплошные нули, а ещё через двадцать лет он целые сутки будет выдавать сплошные единицы.
mihaild
25.01.2016 22:25Если PRG нормальный, то остановка гарантирована (вероятность того, что алгоритм не остановится — ноль), а мат. ожидание времени работы — оптимально с точностью до мультипликативной константы.

nickolaym
25.01.2016 20:05Насчёт равномерности — требуются доказательства!
Ибо разным последовательностям случайных бит соответствуют одинаковые перестановки.
Например, (для n=5)
00000, xyz… = 11111, xyz… = xyz… — потому что, как я уже сказал выше, все-нули и все-единицы — это просто пропуск одного шага
01111, 0111, xyz… = 00111, 01, xyz… — два раза отщепили первый элемент и перетасовали хвост, — это отщепили два элемента, сохранили их порядок, перетасовали хвост…
vasiatka
25.01.2016 22:00В статье сделано моделирование (ака Монте-Карло), распределение перестановок получено равномерное.
В конце статьи есть ссылка на оригинальную статью, там есть доказательства.


dcc0
С описанием пока не очень понятно:
т.е. для n = 7 имеем 7 битов, сгенерированных случайно, допустим: 0101101,
делим. (массивы изначально пустые?! Это был риторический вопрос), получаем P0=[0,0,0], P1[1,1,1,1]
@ все элементы, которым сопоставлены нули заносятся в массив P0, остальные в массив P1@
Перемешиваем… и тут вопрос: что перемешиваем каждый массив в отдельности?
Но там и так все значения одинаковые. Или мы перемешиваем индексы?
vasiatka
Вы немного не поняли. Сопоставить элементам массива биты, не означает записать их в этот массив. Массив Р содержит элементы, которые нужно переставить. В вашем случае будет так:
P=[1,2,3,4,5,6,7]; g=[0,1,0,1,1,0,1];Тогда массивы Р0 и Р1:
P0=[1,3,6]; P1=[2,4,5,7];Нужен ли в статье модельный пример? Мне казалось все достаточно понятным.
dcc0
Да, точно. Перечитал. Спасибо.
Про модельный пример не могу дать однозначного ответа. Нужен ли — зависит, вероятно, от того, на какую аудиторию рассчитан материал. Вообще — легче один разу увидеть, чем 100 раз услышать :).
Если алгоритм — не военная тайна, то можно дать какую-то модель :)