Напоследок, о второй части доклада Surya Ganguli — как теоретическое понимание процесса оптимизации может помочь на практике, а именно, какую роль играют седловые точки (первая часть вот тут, и она совершенно необязательна для чтения дальше).

Disclaimer: пост написан на основе отредактированных логов чата closedcircles.com, отсюда и стиль изложения, и уточняющие вопросы.
Чуть-чуть напомню, что такое седловые точки. В пространстве нелинейных функций есть точки с нулевым градиентом по всем координатам — именно к ним стремится градиентный спуск.
Если у точки градиент по всем координатам 0, то она может быть:
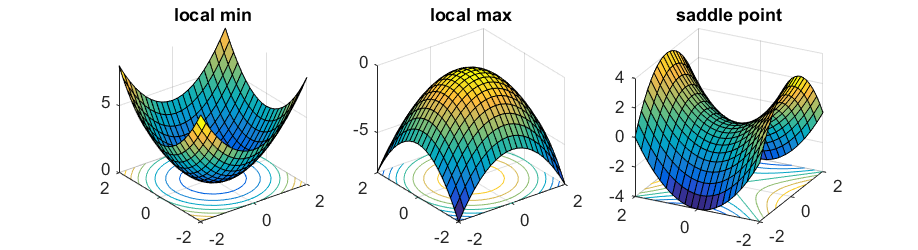
- Локальным минимумом, если по всем направлениями вторая производная положительна.
- Локальным максимумом, если по всем направлениям вторая производная отрицательна.
- Седловой точкой, если по каким-то направлениям вторая производная положительна, а по другим отрицательна.
Итак, нам рассказывают хорошие новости для градиентного спуска в очень многомерном пространстве (каким является оптимизация весов глубокой нейросети).
- Во-первых, подавляющее большинство точек с нулевым градиентом — это седловые точки, а не минимумы.
Это можно легко понять интуитивно — чтобы точка с нулевым градиентом была локальным минимумом или максимумом, вторая производная должна быть одного знака по всем направлениям, но чем больше измерений, тем больше шанс, что хоть по какому-то направлению знак будет другим.
И поэтому большинство сложных точек, которые встретятся — будут седловыми. - Во-вторых, с ростом количества параметров оказывается, что все локальные минимумы довольно близко друг к другу и к глобальному минимуму.
Оба этих утверждения были известны и теоретически доказаны для случайных ландшафтов в больших измерениях.
В сотрудничестве с лабой Yoshua Bengio их получилось экспериментально продемонстрировать и для нейросетей (теоретически пока не осилили).
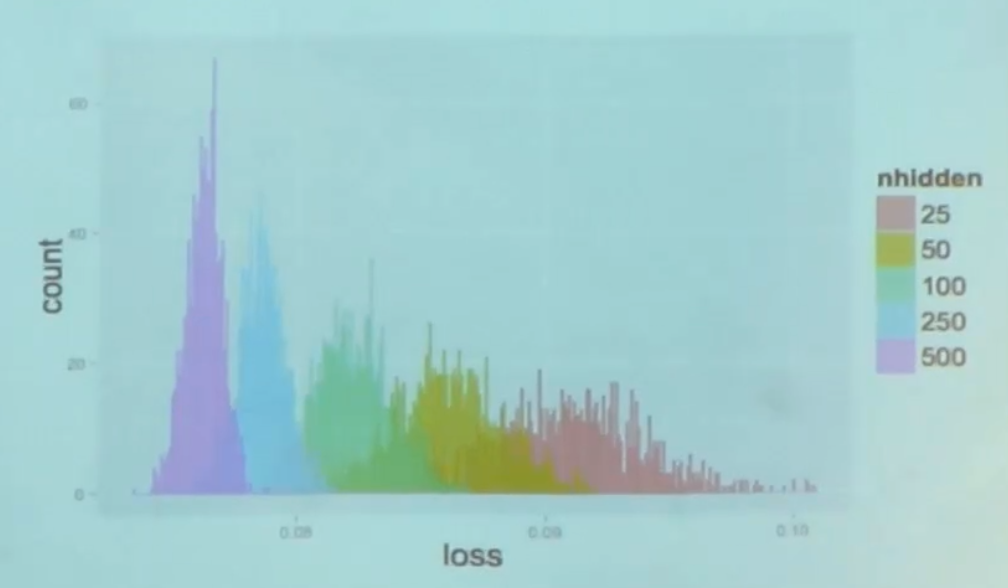
Это гистограмма значений cost function в локальных минимумах, которые получились многократными попытками тренировок из разных точек — чем меньше параметров, тем меньше разброс значений в локальных минимумах. Когда параметров много, разброс резко уменьшается и становится очень близким глобальному минимуму.
Главный вывод — что локальных минимумов бояться не нужно, основные проблемы — с седловыми точками. Раньше, когда мы плохо умели тренировать нейросети, мы думали, что это из-за того, что система скатывается в локальный минимум. Оказывается, нет, мы просто не могли выбраться из седловой точки.
И вот они придумали твик градиентного спуска, который хорошо избегает седловых точек. К сожалению, у них там используется гессиан.
Для необразованных как я, гессиан — это матрица значений попарных вторых производных в точке. Если думать о градиенте как о первой производной для функции от многих переменных, гессиан — вторая.
Александр Власов вот написал хороший туториал про так называемые second order optimizations, к которым относится работа с гессианом.
Разумеется считать гессиан — страшно непрактично для современных нейросетей, поэтому я не знаю как их решение на практике применять.
Второй момент — это они придумали некую теоретически кошерную инициализацию, которая в случае просто линейных систем решает проблему vanishing gradients и дает тренировать сколь угодно глубокую линейную систему за одинаковое количество градиентных шагов.
И мол утверждается, что и для нелинейных систем это тоже помогает. Я, правда, пока не видел упоминаний в литературе успешного использования этой техники.
Ссылки на полные статьи: про оптимизацию градиентного спуска и про улучшенную инициализацию.
В интересное время живем.
Комментарии (13)

pehat
04.05.2016 11:38+1Поясните необразованному, почему так сложно бороться с седловыми точками? Казалось бы, седло – точка неустойчивого равновесия, и малые возмущения в большинстве направлений должны «скатываться» из седла в сторону локального минимума.

Monnoroch
04.05.2016 13:39+3Потому, что вокруг седла во все стороны очень пологое плато и кажется, что все, оптимизация закончилась, когда на самом деле нет.


Monnoroch
У меня всегда было ощущение, что с седловыми точками как раз призваны сражаться модернизированные методы оптимизации с моментом и прочими наворотами. На интуитивном уровне кажется, что вторые производные лучше момента только в теории (ну и может на практике только количественно и не очень уж сильно), ведь добавление момента в каком-то смысле делает оптимизационный метод второго порядка: с «ускорением».
Не одинаковое, а ограниченно растущее. Это значит, что в какой-то момент увеличение числа слоев перестает увеличивать время обучения, но вот что это за момент и насколько скоро он наступает — еще вопрос. Теоретический результат хорош, но применим ли он к нелинейным сетям и к глубине сетей принятой в жизни пока не ясно.
sim0nsays
Все так, RMSProp, adagrad и прочее — как раз для этого, но не сказать, что они эту задачу всегда решают успешно. Когда шума много, маленький сигнал из правильного направления легко забить :(

Про второе — хм, он по-моему в докладе прямо говорил, что мол indepedent, график показывал —
Или вы прочитали статью и это все обман?
Monnoroch
Я прочитал статью и там есть очень другая картинка:

Какая-то из них врет и вот эта мне кажется гораздо более правдоподобной :)
sim0nsays
Стоять! Это была статья про их улучшенный метод градиентного спуска, это вообще не про иницализацию. Инициализацию они обсуждают тут — http://arxiv.org/pdf/1312.6120.pdf, и там натурально независимо от глубины (искать по словам orthogonal initialization).
Поправлю пост
Monnoroch
А вот и не стоять, моя картинка как раз из правильной статьи про инициализацию.
sim0nsays
Ок, но она же вроде из секции до init conditions? Т.е. supposedly они при получении этого графика ее не применяли. А дальше там те же графики, что и на скрине, который я привел выше.
Monnoroch
И это тоже не правда, вот часть описания эксперимента на моей картинке:
То есть, они уже тут применяют ключевую идею статьи про decoupled initial conditions. Возможно, дальше они дополнительно сделали что-то еще и получили еще более крутые результаты, как на вашей картинке, но я пока не понял, что же именно.
sim0nsays
Прежде всего, спасибо за обсуждение — пришлось таки прочитать статью :)
Насколько я понимаю, этот график из секции про экспериментальное подтверждение тезиса, что с ростом глубины сети время тренировки в количестве эпох выходит на константу. Она у них довольно высокая, потому что они выбрали значение главной моды маленьким, а время схождения от нее зависит квадратично.
В следующей секции они сначала исследуют возможность делать unsupervised pretraining на input set, который мол получает начальные значения с модой близкой к 1, поэтому сходится гораздо быстрее. Про это у них дальше картинка:
И далее сноска:
Что видимо как раз отвечает на обсуждаемый нами вопрос.
Далее они предлагают вместо дорогой процедуры pretraining использовать тупо ортогональные матрицы для весов (что отличается от depoupled conditions, если я не путаю, потому что decoupled conditions зависят от атупута тоже), и они сходятся тоже с константой скоростью, видимо у них тоже мода хорошая.
Monnoroch
Спасибо, я тоже уже вчитался еще раз в детали статьи и пришел к тем же выводам. Однако, мне все равно не верится, что эти результаты обобщатся на произвольные модели. Все-таки, обучить модель любого размера за пару-тройку эпох (судя по графику) — это какая-то фантастика.
sim0nsays
О да, я тоже полон сомнений. В случае нелинейных моделей и других датасетов все может легко развалиться. Тем более, попробовать просто, а что-то никто не рапортует об успехах.
Monnoroch
Я попробую, как время будет на моих RCGAN-ах, с которыми я сейчас играю и которые реально сложно оптимизировать.