Аннотация

В статье рассмотрены основы статистической обработки сигналов и методы их оптимальной обработки* на фоне шума.

Введение

Основной задачей радиотехники является приём, передача и обработка информации с использованием в качестве переносчика – радиосигнала. Главное требование, предъявляемое к радиотехническим системам – получение своевременной и достоверной информации от источника к потребителю. Однако этому мешает физика принципов работы приёмопередающих устройств и среды распространения сигнала, суть которой заключается во флюктуации физических параметров системы и случайным значением принимаемого сигнала, имеющего шумовую составляющую, также относящуюся к стохастическим процессам.

На текущий момент, самый эффективный способ различения полезных сигналов на фоне шумов и помех является оптимальная обработка, реализуемая, как правило, сравнением принимаемой входной реализации с априорно известной формой полезного сигнала. При этом шумы, которые по своей природе процесс слабокоррелированный, вносят меньший вклад в величину, показывающую степень этого сравнения и называющуюся коэффициентом корреляции. Таким образом, любая задача обнаружения сводится к проверке минимум двух гипотез. В общем случае задача обнаружения состоит из двух гипотез: H_0 – сигнал отсутствует на входе приёмного устройства, H_1 – сигнал присутствует на входе приёмного устройства. Различные алгоритмы обнаружения обеспечивают различную вероятность правильного обнаружения P{d_1/H_1} при различных прочих статистических параметрах. Для сравнения эффективности алгоритмов обнаружения существуют критерии, а так как обрабатываются вероятностные величины, то характер этих критериев статистический. Иными словами критерий можно определить как мерило сравнения.

Статистические критерии обнаружения

Большая часть алгоритмов обнаружения радиолокационных целей включают в себя следующие этапы:

1. Прием входной реализации
2. Формирование порога на основе априорной или апостериорной информации.
3. Оптимальная фильтрация входной реализации
4. Принятие решения о наличии сигнала/цели

При этом очередность приёма входной реализации и формирования порога зависит непосредственно от типа алгоритма. Алгоритмы, формирующие порог на основе апостериорной информации о принятой входной реализации называют адаптивными [1]. Критерий выбирается эмпирически исходя из типа задачи. Например: при выборе места работы обычно рассматривают два критерия:

• Максимума отношения заработанных денег к затраченной силе.
• Максимума удовольствия, получаемого от работы.

К сожалению, современные реалии ставят в приоритет такого специалиста, навыки которого позволяли бы как можно быстрее выпустить продукцию и максимизировать прибыль компании. И зачастую второй критерий либо отбрасывается, либо при анализе ситуации ему присваивается низкий приоритет. Показатель, в данном случае, определяющий приоритет критериев, называется его мощностью.

В математической статистике мощность критерия определяется, как вероятность не совершить ошибку второго рода при принятии решения. В нашем случае ошибка второго рода — это не устроится на оптимальную для себя работу, в общем же случае это ложное принятие за истину события соответствующего гипотезе H_0.

Разумеется, универсальных критериев не существует. Так, например, критерий, имеющий наибольшую мощность, в решении одной задачи, в решении другой может оказаться наихудшим по этому показателю.

Критерий минимального среднего риска (критерий Байеса)

Рис.1 График распределения условной плотности вероятности наличия W(U|A=1) и отсутствия W(U|A=0) с вероятностями ошибок

Пусть A = 1 соответствует наличию сигнала s(t), а A = 0 – его отсутствию. Множество решений d вырождается в два: d_0 >A=1 and d_1>A=0.
При решении задачи бинарного обнаружения задача эквивалентна проверке гипотезы H_1 о том, что А = 1, при альтернативной гипотезе H_0 о том, что А = 0, а функция потерь переходит в квадратную матрицу:



Таким образом, условный риск при A = 0 равен r_0= C_00 P{d_0/H_0 }+ C_01 P{d_1/H_0 }=C_00 (1-P{d_1/H_0 })+ C_01 P{d_1/H_0 }, а при A = 1 равен r_1= C_10 P{d_0/H_1 }+ C_11 P{d_1/H_1}=C_10 (1-P{d_1/H_1} )+C_11 P{d_1/H_1}, где P{d_1/H_1} – вероятность правильного обнаружения, а P{d_1/H_0 } – вероятность ложной тревоги.

Средний риск определяется как r ?=qr_0+pr_1, где q – априорная вероятность отсутствия сигнала, а p – априорная вероятность присутствия сигнала и определяет средние потери при ложной тревоге и пропуске цели [2]. Например: при использовании такого критерия для выставления порога срабатывания пожарной сигнализации, стоимость риска при ложной тревоге – вызов пожарной службы, а при пропуске – стоимость вещей в сгоревшей квартире или офисе.

На рис.1 проиллюстрированы графики распределения плотности вероятности при наличии и отсутствии сигнала, также выделены зоны, площадь которых численно равна вероятностям ошибок при принятии решения. Ввиду стохастической природы явлений рассматриваемых в данном примере, распределения имеют ненулевую дисперсию. Согласно критерию минимального среднего риска лучшим алгоритмом обнаружения сигнала будет тот, у которого величина r ? будет минимальна [2].

Критерий максимума апостериорной вероятности (максимального правдоподобия)

Этот критерий получается из критерия минимального среднего риска при условии, что потери при совершении ошибки обратно пропорциональны вероятности их совершения C_01=1/P{d_0}, C_10=1/P{d_1}. При этом порог оптимального обнаружителя выставляется таким образом, чтобы минимизировать сумму вероятностей ошибок P_ош=P{d_0/H_1 }+P{d_1/H_0 } (см рис.2).


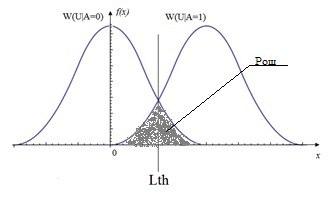
Рис.2 График распределения условной плотности вероятности наличия W(U|A=1) и отсутствия W(U|A=0) с вероятностью ошибки

Двухпороговый критерий Вальда

В случаях, когда большую роль играет время наблюдения за процессом, например при наличии нескольких каналов и одного обнаружителя или круговом обзоре РЛС, применяют критерий последовательной проверки гипотез Вальда также известный под названием двухпороговый.


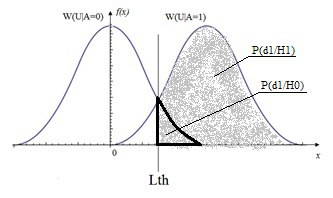
Рис.3 График распределения условной плотности вероятности наличия W(U|A=1) и отсутствия W(U|A=0) с вероятностью правильного обнаружения и вероятностью ложной тревоги

По этому критерию область определения вероятности делится на три подобласти, разделяемыми двумя порогами, определяемыми вероятностями правильного обнаружения и ложной тревоги (см.рис 3):
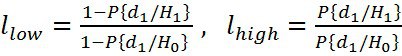
Критерий Вальда является оптимальным в смысле минимизации среднего времени наблюдения по большому количеству экспериментов [4]. Так как наиболее предпочтительным для радиолокации является сокращение длительности процедуры обнаружения, современные реалии ведут к всё более активному использованию этого критерия [5].

Критерий Неймана-Пирсона

Большим минусом критериев Байесовского класса является необходимость априорного знания элементов матрицы потерь. Например: при пропуске вражеского бомбардировщика на союзную территорию стоимость рисков не поддается исчислению.

В критерии Неймана-Пирсона фиксируется время обнаружения. Оптимальным будет алгоритм с максимальной вероятностью правильного обнаружения P{d_1/H_1 }, при условии, что вероятность ложной тревоги P{d_1/H_0 } не превышает заданной величины [6].

В виду того, что критерий Неймана-Пирсона не требует знания априорных вероятностей ситуаций A = 1 и A = 0, в радиолокации его используют одним из основных [5].

Заключение

При разработке обнаружителей очень важно осознанно выбирать критерий оптимальности, ведь, как уже упоминалось ранее, каждый критерий имеет максимальную мощность в какой-либо определенной ситуации и применение иных может привести к нежелательным последствиям.

Список использованных источников:

[1] Bulyakulov R.R. The adaptive threshold device // Processing of the 2014 IEEE North West Russia Section Young Researches in Electrical and Electronic Engineering Conference. P.165.
doi: 10.1109/EIConRusNW.2016.7448237
[2] Бакулев, П.А. Радиолокационные системы. Учебник для ВУЗов / П.А. Бакулев; М.: Радиотехника, 2004. – 46 с.
[3] Юревич, Е.И. Теория автоматического управления / Е.И. Юревич; М.: Энергия, 1969
[4] Богатырев, А.А. Стандартизация статистических методов управления качеством / А. А. Богатырев, Ю. Д. Филиппов; М.: Изд-во стандартов, 1989. – 42 с.
[5] Храменков, А.С. Сопоставительный анализ радиолокационных обнаружителей, основанных на критерии неймана-пирсона и последовательном критерии отношения вероятностей /А.С. Храменков, С.Н. Ярмолик // доклады БГУИР №6(76) Минск, 2013.
[6] Васильев, К.К. Методы обработки сигналов: Учебное пособие / К.К. Васильев; Ульяновск, 2001.