Как может показаться, анализ сигналов и данных — тема достаточно хорошо изученная и уже сотни раз проговоренная. Но есть в ней и некоторые провалы. В последние годы словом «энтропия» бросаются все кому не лень, толком и не понимая, о чем говорят. Хаос — да, беспорядок — да, в термодинамике используется — вроде тоже да, применительно к сигналам — и тут да. Хочется хотя бы немного прояснить этот момент и дать направление тем, кто захочет узнать чуть больше об энтропии. Поговорим об энтропийном анализе данных.
В русскоязычных источниках очень мало литературы на этот счет. А цельное представление вообще получить практически нереально. Благо, моим научным руководителем оказался как раз знаток энтропийного анализа и автор свеженькой монографии [1], где все расписано «от и до». Счастью предела не было, и я решила попробовать донести мысли на этот счет до более широкой аудитории, так что пару выдержек возьму из монографии и дополню своими исследованиями. Может, кому и пригодится.
Итак, начнем с начала. Шенноном в 1963 г. было предложено понятие меры усредненной информативности испытания (непредсказуемости его исходов), которая учитывает вероятность отдельных исходов (до него был еще Хартли, но это опустим). Если энтропию измерять в битах, и взять основание 2, то получим формулу для энтропии Шеннона
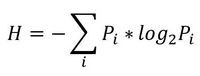, где Pi это вероятность наступления i-го исхода.То есть в этом случае энтропия напрямую связана с «неожиданностью» возникновения события. А отсюда вытекает и его информативность — чем событие более предсказуемо, тем оно менее информативно. Значит и его энтропия будет ниже. Хотя открытым остается вопрос о соотношениях между свойствами информации, свойствами энтропии и свойствами различных ее оценок. Как раз с оценками мы и имеем дело в большинстве случаев. Все, что поддается исследованию — это информативность различных индексов энтропии относительно контролируемых изменений свойств процессов, т.е. по существу, их полезность для решения конкретных прикладных задач.
Энтропия сигнала, описываемого некоторым образом (т.е. детерминированного) стремится к нулю. Для случайных процессов энтропия возрастает тем больше, чем выше уровень «непредсказуемости». Возможно, именно из такой связки трактовок энтропии вероятность->непредсказуемость->информативность и вытекает понятие «хаотичности», хотя оно достаточно неконкретно и расплывчато (что не мешает его популярности). Встречается еще отождествление энтропии и сложности процесса. Но это снова не одно и то же.
Едем дальше.
Энтропия бывает разная
- термодинамическая
- алгоритмическая
- информационная
- дифференциальная
- топологическая
Все они различаются с одной стороны, и имеют общую основу с другой. Конечно, каждый вид применяется для решения определенных задач. И, к сожалению, даже в серьезных работах встречаются ошибки в интерпретации результатов расчета. А все связано с тем, что на практике в 90% случаев мы имеем дело с дискретным представлением сигнала непрерывной природы, что существенно влияет на оценку энтропии (на деле там в формулке появляется поправочный коэффициент, который обычно игнорируют).
Для того, чтобы немного обрисовать области применения энтропии к анализу данных, рассмотрим небольшую прикладную задачку из монографии [1] (которой нет в цифровом виде, и скорей всего не будет).
Пусть есть система, которая каждые 100 тактов переключается между несколькими состояниями и порождает сигнал x (рисунок 1.5), характеристики которого изменяются при переходе. Но какие — нам не известно.
Разбив x на реализации по 100 отсчетов можно построить эмпирическую плотность распределения и по ней вычислить значение энтропии Шеннона. Получим значения, «разнесенные» по уровням (рисунок 1.6).
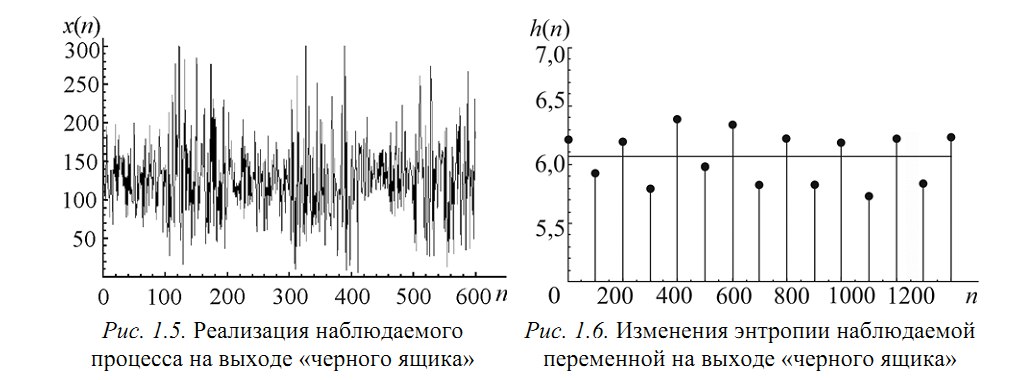
Как можно видеть, переходы между состояниями явно наблюдаются. Но что делать в случае, если время переходов нам не известно? Как оказалось, вычисление скользящим окном может помочь и энтропия так же «разносится» на уровни.В реальном исследовании мы использовали такой эффект для анализа ЭЭГ сигнала (разноцветные картинки про него будут дальше).
Теперь еще про одно занятное свойство энтропии — она позволяет оценить степень связности нескольких процессов. При наличии у них одинаковых источников мы говорим, что процессы связаны (например, если землетрясение фиксируют в разных точках Земли, то основная составляющая сигнала на датчиках общая). В таких случаях обычно применяют корреляционный анализ, однако он хорошо работает только для выявления линейных связей. В случае же нелинейных (порожденных временными задержками, например) предлагаем пользоваться энтропией.
Рассмотрим модель из 5ти скрытых переменных(их энтропия показана на рисунке ниже слева) и 3х наблюдаемых, которые генерируются как линейная сумма скрытых, взятых с временными сдвигами по схеме, показанной ниже справа. Числа-это коэффициенты и временные сдвиги (в отсчетах).
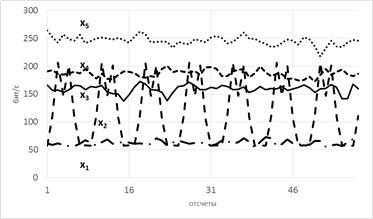
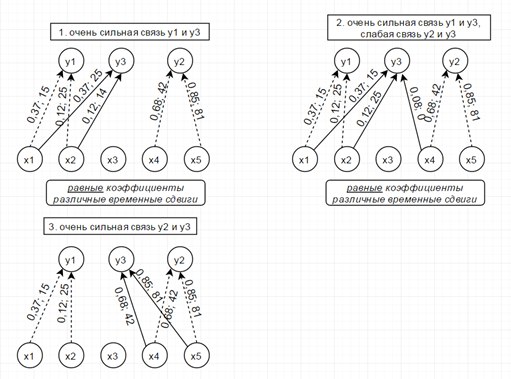
Так вот, фишка в том, что энтропия связных процессов сближается при усилении их связи. Черт побери, как это красиво-то!
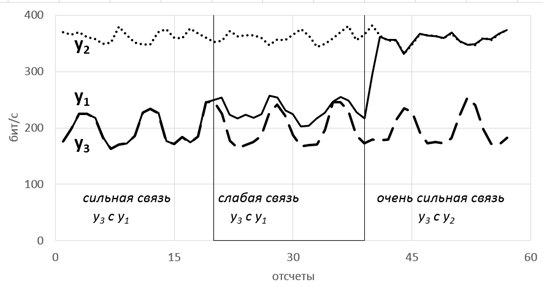
Такие радости позволяют вытащить практически из любых самых странных и хаотичных сигналов (особенно полезно в экономике и аналитике) дополнительные сведения. Мы их вытаскивали из электроэнцефалограммы, считая модную нынче Sample Entropy и вот какие картинки получили.
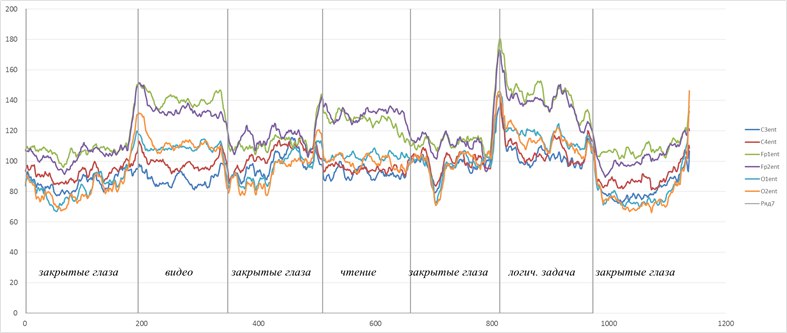
Можно видеть, что скачки энтропии соответствуют смене этапов эксперимента. На эту тему есть пара статей и уже защищена магистерская, так что если кому будут интересны подробности — с радостью поделюсь. А так по миру по энтропии ЭЭГ ищут уже давно разные вещи — стадии наркоза, сна, болезни Альцгеймера и Паркинсона, эффективность лечения от эпилепсии считают и тд. Но повторюсь-зачастую расчеты ведутся без учета поправочных коэффициентов и это грустно, так как воспроизводимость исследований под большим вопросом (что критично для науки, так то).
Резюмируя, остановлюсь на универсальности энтропийного аппарата и его действительной эффективности, если подходить ко всему с учетом подводных камней. Надеюсь, что после прочтения у вас зародится зерно уважения к великой и могучей силе Энтропии.
P.S. При наличии интереса, могу немного подробней поговорить в следующий раз об алгоритмах расчета энтропии и почему энтропию Шеннона сейчас смещают более свежие методы.
Литература
1. Цветков О.В. Энтропийный анализ данных в физике, биологии и технике. СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2015. 202 с.
2.Abasolo D.,Hornero R., Espino P. Entropy analysis of the EEG background activity in Alzheimer’s disease patients // Physiological Measure-ment. 2006. Vol. 27(3). P. 241 – 253. epubs.surrey.ac.uk/39603/6/Abasolo_et_al_PhysiolMeas_final_version_2006.pdf
3. 28. Bruce Eugene N, Bruce Margaret C, Vennelaganti S. Sample entropy tracks changes in EEG power spectrum with sleep state and aging // Journal of Clinical Neurophysiology. 2009. Vol. 26(4). P. 257 – 266. www.ncbi.nlm.nih.gov/pubmed/19590434
4. Энтропийный анализ как метод безгипотезного поиска реальных (гомогенных) социальных групп (О. И. Шкаратан, Г. А. Ястребов) www.sociologos.ru/metody_i_tehnologii/Razdel_Analiz_dannyh/Statisticheskij_analiz/Entropijnyj_analiz_kak_metod_bezgipoteznogo_poiska_realnyh_gomogennyh_socialnyh
5. Энтропийные и другие системные закономерности: Вопросы управления сложными системами. Прангишвили И.В. apolov-oleg.narod.ru/olderfiles/1/Prangishvili_I.V_JEntropiinye_i_dr-88665.pdf
Комментарии (40)
mickvav
17.07.2016 22:20Вот чего не понял — как из картинки 1.5 получается картинка 1.6?
YuliyaCl
17.07.2016 22:28Исходную последовательность разбиваем на «куски» по 100 отсчетов. По каждому строим эмпирическую плотность распределения вероятности Pi и с ней считаем энтропию Шеннона по формулке.
mickvav
18.07.2016 11:51Ок, получили 100 float-ов. Скорее всего, все разные. Вероятность каждого из исходов — 1/100. Как получается, что ваша формула дает разные числа?
mickvav
18.07.2016 11:53Да, и чем именно 100 отсчетов так уж примечательны? 200 будет лучше или хуже? Почему?
YuliyaCl
18.07.2016 19:22100-так как берется система, каждый 100й отсчет переключающаяся в другое состояние(условно их у нас два в примере). И для каждого из этих состоянии имеет место свое распределение вероятности. Вот оно то и будет влиять на значение расчетной энтропии.
mickvav
19.07.2016 09:30+2А если нет априорного знания о том, как там система ведёт себя под капотом, откуда взять этот период? И еще раз повторю не отвеченный вопрос — как вы по 100 float-ам распределение вероятности строите? Если строите гистограмму, то какую и из каких соображений выбираете её параметры?
Sergey_Kovalenko
17.07.2016 23:05+1Что касается бинарных последовательностей, до сих еще никто не справились с задачей дать удовлетворительную меру сложности единичного конструктивного объекта в себе, колмогоровская сложность безотносительно машины или языка определена лишь для неограниченно усложняющихся последовательностей таких объектов. Иными словами, если наперед задан объект, то можно предъявить машину, относительно которой его сложность равна нулю, как бы он интуитивно сложен не был, и машину, относительно которой сложность этого объекта будет невероятно большой, даже если он интуитивно прост.
Простите, а какая главная мысль статьи? Второй вопрос — как все-таки строится модель энтропийного передатчика для конкретного процесса, например если процесс на осциллографе — правильная синусоида?YuliyaCl
17.07.2016 23:21Да, относительность она везде)
Мысль главная-это рассказать о разноплановости энтропии как понятия(не каждый это знает), и отметить некоторые подводные камни. Ну и вдруг кому-то информация пригодится в своих исследованиях.
Насчет второго вопроса уточните, пожалуйста, что вы имеете ввиду под моделью-аналитическое выражение али что то другое?Sergey_Kovalenko
18.07.2016 14:49Если следовать примеру выше и разбить область значений синусоиды на небольшие участки, то получится, что принимая любое значение кроме крайних, почти равновероятен как переход в состояние с большим значением, так и переход в состояние с меньшим. Выходит, что синусоидальный сигнал, будучи полностью предсказуемым, имеет ненулевую энтропийную мощность в качестве марковского передатчика?
Sergey_Kovalenko
18.07.2016 15:02Энтропийная мощность марковского передатчика (энтропия Шеннона) — абсолютная не зависящая не от чего величина, применимая всюду, где по крайней мере можно утверждать вероятностный либо статистически устойчивый характер процесса.
К примеру взяв 20 типографских оттисков буквы «а» 15 — буквы «б» и 65 — буквы «в» с помощью энтропийной мощности в отсутствие всякой вероятности Вы можете подсчитать количество различных слов длины 100, составленных из этих оттисков.
sgenie
18.07.2016 01:39А можно текст магистерской где-нибудь наити?
YuliyaCl
18.07.2016 01:43В библиотеке университета(ЛЭТИ) лежит электронная запись, но могу прислать по почте с честным обещанием, что будете ссылаться при использовании)
Astronomikon
18.07.2016 02:13поделитесь своей работой) ссылки на ваше авторство обещаю)
info@astronomikon.ru
Vinchi
18.07.2016 05:37может напишите ссылку на его работу или пошлете на мою почту? :) turyev.roman@gmail.com
Alter2
18.07.2016 10:04Честно сказать так и не понял зачем было вводить эту чисто статистическую величину когда есть прекрасно зарекомендовавшая себя дисперсия с абсолютно тем же применением что и рассмотренное в статье (поиск корелляции).
YuliyaCl
18.07.2016 10:08В некоторых случаях действительно корреляцией можно обойтись. Но как и отмечала-только в случае линейности связи. Нелинейные она не видит.
Проверяли хотя бы на моделях, одна из которых тут представлена. Энтропия отражает степень связности, а корреляции нет между сигналами вообще(наблюдаемые переменные генерировались на основе независимых скрытых ).
Так что основное преимущество перед дисперсионным методом именно такое.
Ares_ekb
18.07.2016 10:21+1Например, принцип максимума энтропии используется для определения распределения вероятностей при некоторых известных макро ограничениях. В своё время этот принцип произвел на меня огромное впечатление своей простотой и возможностями. Я очень давно этим не занимался и вряд ли смогу привести какие-то примеры. Можно погуглить maxent.
Кстати, там используется именно энтропия Шеннона, в связи с чем очень интересно это:
P.S. При наличии интереса, могу немного подробней поговорить в следующий раз об алгоритмах расчета энтропии и почему энтропию Шеннона сейчас почти не используют.
Я был уверен, что Шенноновская энтропия повсеместно используется.YuliyaCl
18.07.2016 10:51+1Скорее некорректно немного сказала, десятилетия два назад появились новые метод расчета, показывающие в ряде задач бОльшую эффективность(аппроксимированная и выборочная в ТОП-ах). Поэтому есть тенденция перехода на них. Но конечно для ряда задач Шенноновская также применима. Подправлю, пожалуй)
buriy
18.07.2016 10:51То есть, если я правильно понял, вы считаете, что если у вас есть две функции H от распределения вероятностей перехода между состояниями, то они друг с другом как-то «связаны»?
Даже если не говорить про способы влияния количества пиратов на глобальное потепление (ваше определение «связанности» явно означает не причинно-следственную связь), можно легко подобрать случай, когда энтропия одной функции будет в два раза больше или меньше другой, но из первой функции можно будет прекрасно предсказать вторую с любой наперёд указанной точностью, и наоборот.
Всё же одним параметром распределение вероятностей не опишешь.
uhharski
18.07.2016 11:48Спасибо за статью, хотелось побольше узнать о алгоритме вычисления степени связности нескольких процессов с помощью энтропии.
Dimchansky
19.07.2016 00:53Есть ли где-то в электронном виде «Цветков О.В. Энтропийный анализ данных в физике, биологии и технике»? Тираж, смотрю, совсем небольшой.
gaki
19.07.2016 05:38Я шо-то не понял… первая формула определяет битовую размерность числа всех возможных исходов?
К примеру, подбрасываем монету, возможных исходов 2, вероятность каждого = 0.5, логарифм = -1, H = -(0.5*-1 + 0.5*-1) = 1. Действительно, можно описать все (два) исхода одним битом, который либо ноль, либо единица.
Или вот, допустим, я выпил йаду -> у меня один исход (смертельный) с вероятностью 1, логарифм = 0, H = 0. Т. е., вообще ни одного бита не нужно, и так всё ясно… Хотя нет, что-то не сходится — формально же исходов всё равно два — умер (вероятность 1)/не умер (вероятность 0), и нужно будет посчитать несуществующий логарифм нуля?..buriy
19.07.2016 11:30Если логарифм нуля (минус бесконечность) умножить на ноль, получим в данном случае ноль.
X*ln X -> 0 при X -> 0
perfect_genius
19.07.2016 08:32+2Очередная статья про энтропию, написанная сложным языком. Продолжаем ждать простую статью.
Neurocell
19.07.2016 09:14Любопытно было бы взглягуть на магистерскую (wissensaft at protonmail dot com), но последняя картинка в статье выглядит так, как будто вы нашли различие по «ЭЭГ» без глазных артефактов и с оными. Подругому взлет энтропии по Fp1/Fp2, при стабильных O1/O2 во время визуальной нагрузки прям и не объяснить :). Шутки в сторону, главная причина имхо по которой энтропия не светится в физиологических журналах приличного импакта (5+), в том что чаще всего данные могут быть объяснены моделью с более тривиальными параметрами: мощность, когерентность и т.п. Ну или не могут быть объяснены вовсе. В статье, на рисинках 1.5 и 1.6., на глаз, амплитудная огибающая тоже вполне себе предсказатель, исчитать в 100 раз дешевле. (На «сравнительных» русунках, кстати, масштаб по абсциссе не соблюден. Я был бы рецензентом — наругался бы.)
TimeCoder
23.07.2016 11:55На тему энтропии меня давно мучает один вопрос, буду признателен за мысли. Что насчет изменения энтропии Вселенной (да, я читал Хокинга)? А лучше, ее относительно малой части: солнечной системы. Если посмотреть тенденцию: было просто газопылевое облако, появилась звезда, образовались тяжелые элементы и планеты, вода, простые организмы, сложные организмы, разумный человек, цивилизация.
Как Вы считатете, каждый следующий шаг «ожидаем»?
Если да, то в основу реальности вшит механизм обеспечения ее эволюции на всех уровнях (не только биологическом), если нет — значит энтропия мира падает (за счет чего?).Olm
26.07.2016 04:57А почему вы считаете солнечную систему замкнутой или изолированной? Теперь пропало противоречие? Помимо этого с термодинамической точки зрения все «нормально» даже в наших масштабах — солнце постепенно остывает, планета напротив нагревается…
TimeCoder
26.07.2016 09:481. Думаю, что изолированных систем в природе вообще нет, речь об относительной изолированности. В трудах Н.А. Козырева упоминались галактики, расстояния между которыми столь огромны, что их слабым взаимодействием в данном вопросе можно пренебречь. Второе начало термодинамики применимо только к абсолютно замкнутой системе? Если таковых в реальности не существует, значит это правило в природе не работает? Если допускается некоторая открытость — какова мера? Какую систему можно считать достаточно замкнутой?
2. Вселенная — изолированная система? Если честно, мне не нравятся трюки с термодинамической трактовкой энтропии. По бумаге, энтропия падает, но никакая формальная модель меня не убедит в том, что текущее состояние Вселенной — более хаотичное, чем кипящий океан энергии после большого взрыва. Структура материи в пространстве и динамика процессов во времени невероятно сложная, живые организмы поражают уровнем организации. Процессы, которые протекают в организме человека несопоставимо сложнее, чем процессы на этапе зарождения звездных систем (сравните термоядерный синтез и процесс репликации ДНК). Мир становится все более сложным и высокоорганизованным, и вовсе не думает кануть в пучине тепловой смерти. Что не так с энтропией?
qw1
26.07.2016 13:02Относитесь к энтропии не как к мере хаоса, а как к мере непредсказуемости.
Чьё поведение сложнее предсказать, кипящего океана или человеческого социума? Если второе, значит энтропия со временем выросла.
Ares_ekb
26.07.2016 21:32На эту тему вспоминается книга «Физика процессов эволюции» и книги по самоорганизации Хакена. Я правда их очень давно читал и ничего не помню ) Кстати, у Хакена не плохо описан принцип максимума информационной энтропии.
У меня отложилось какое-то представление, оно может быть ошибочным. Скажем, если на склон пирамидки положить шарик, то он просто скатится вниз по склону. Если положить шарик на вершину пирамидки, то он тоже скатится вниз, но направление скатывания будет зависеть от малейших флюктуаций. Т.е. поведение становится уже гораздо более сложным.
По мере остывания вселенной, уменьшения её плотности этот «ландшафт» из пирамидок и ямок изменяется нелинейно. Появляются новые точки неустойчивости, точки бифуркации — считай точки свободы, неопределенности. Причем, эти точки каким-то образом могут между собой синхронизироваться и возникают разные пространственные и временные структуры. В упомянутых книгах приводятся примеры.
Не знаю на сколько это корректный пример. Попробуйте вытянуть перед собой руки ладонями вниз. Одновременно на правой руке опустите указательный палец вниз, а средний поднимите вверх, а на левой наоборот — средний вниз, указательный — вверх. Потом измените положение пальцев на противоположное. И делайте так, постепенно увеличивая скорость. В какой-то момент движение рук синхронизируется, и оба указательных (или средних) пальца будут опускаться (подниматься) одновременно. Или если двигать пальцами на разных руках в разных фазах, то постепенно фазы выровняются. Скорость движения пальцами — это некий внешний параметр, который постепенно изменяется (увеличивается), что в некоторый момент приводит к качественному изменению поведения пальцев (системы), они синхронизируются друг с другом.
Так же и со вселенной. Она постепенно остывает. Но при этом происходят разные нелинейные процессы, в которых возникают точки неустойчивости, в которых малейшие флюктуации могут приводить к появлению разных пространственных и временных структур.
Snuff
Спасибо за интересную статью! Было бы интересно почитать статьи на тему практического применения алгоритмической энтропии. И где можно найти книгу [1]?
YuliyaCl
Благодарю!
По поводу алгоритмической энтропии-она особо не применяется в чистом виде в анализе экспериментальных данных, так как не существует (насколько мне известно) универсального алгоритма вычисления алгоритмической сложности произвольной бинарной последовательности. Но наблюдаются связи между алгоритмической и вероятностной энтропией. Можно еще почитать исходную статью Колмогорова http://www.mathnet.ru/links/33d1dd58ea91b3b7cccac275fe0a8970/ppi68.pdf и тут http://iitp.ru/upload/publications/6123/vyugin_kolm.pdf (ссылки красиво не вставляются, извиняюсь)
Книгу можно найти, скорее всего, в киоске СПбГЭТУ «ЛЭТИ», но это нужно уточнить. На неделе выясню и подскажу подробнее. А вы из какого города? И чем занимаетесь? Может, получится по почте отправить, если нужно.
salas
не существует (насколько мне известно) универсального алгоритма вычисления алгоритмической сложности произвольной бинарной последовательности
Да, в точном математическом смысле колмогоровская сложность невычислима (верно даже более сильное утверждение: любая вычислимая оценка её снизу ограничена). Но можно получить любопытные результаты, подменив её на оценку сверху: длину строки после сжатия bzip2. Не знаю, пошла ли эта идея дальше экспериментов по ссылке.