В начале несколько вводных слов. Асинхронными можно называть любые схемы без внешнего тактирования. При этом различные виды асинхронных схем используют разный принцип работы, и самосинхронные схемы – всего лишь одна из их разновидностей. Под самосинхронными обычно понимают т.н. полумодулярные схемы, из-за возможности их представления в виде алгебраических структур, составляющих полумодулярные решетки (да простят меня математики за возможные неточности). Одна из особенностей полумодулярных (читать — самосинхронных) схем – независимость от задержек, что на практике означает работоспособность схемы в любых условиях, при которых транзисторы способны переключаться. Впрочем, никто не мешает проектировать самосинхронные схемы на механических реле или любых других перключателях. Не секрет, что разрабатывать такие схемы очень сложно, но зато им не грозит отказ из-за перегрева, к примеру, или эффектов старения.
С введением всё, и можно переходить к практике. По способу проектирования все самосинхронные схемы можно разделить на две группы – автоматы управления, и схемы с большим количеством логики. Откуда берется такое разделение. Автоматы управления, это несложные устройства вроде счетчиков, защелок, триггеров, или каких-то небольших контроллеров. Эти устройства в основном проектируют вручную с помощью сетей Петри (язык описания параллельных динамических процессов), а затем синтезируют в Petrify или других тулах. Под схемами с большим количеством логики следует понимать привычные всем узлы вычислительных устройств: контроллеры периферии, ПДП, блоки арифметики, да все что угодно, где используется умножение, сложение, сравнение, мультиплексирование и т.д. Подобные схемы слишком сложно описываются сетями Петри, и проектируются иначе (это тема отдельного цикла публикаций, а то и целого учебника). Поэтому начнем с азов, с сетей Петри.
Возьмем в качестве примера простейший самосинхронный счетный триггер. Как и все самосинхронные схемы, он работает по тому же принципу, что и кольцевой генератор на инверторах:
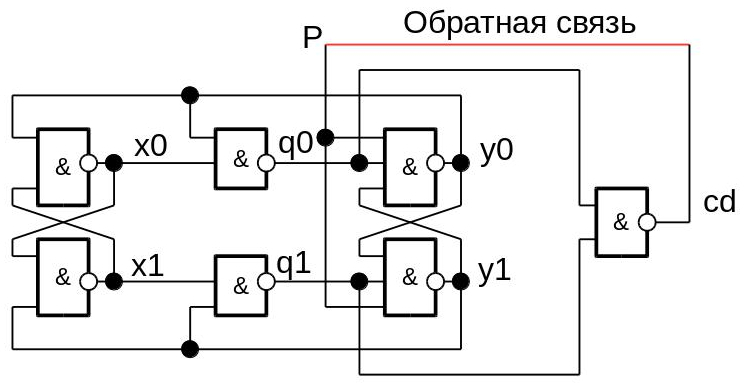
Сигнал P является счетным, сигналы x0,x1,y0,y1 – внутренними, пара {q0,q1} – выходные сигналы счетчика, а cd – индикатор окончания переходных процессов в схеме. Если сигнал cd замкнуть на счетный вход P, автомат будет работать бесконечно. Кто желает, может в этом убедиться при помощи привычного всем моделирования:
`timescale 1ns/10ps
module sim();
wire P,cd;
counter dut(.P(P), .cd(cd));
assign P = cd;
initial begin
force P=0;
force dut.x0=0;
force dut.x1=1;
#2;
release P;
release dut.x1;
release dut.x0;
end
endmodule
module counter(
input wire P,
output wire cd
);
wire x0, x1, y0, y1, q0, q1;
nand2 U1 (.A(y0), .B(x1), .Y(x0));
nand2 U2 (.A(y1), .B(x0), .Y(x1));
nand2 U3 (.A(y0), .B(x0), .Y(q0));
nand2 U4 (.A(y1), .B(x1), .Y(q1));
nand3 U5 (.A(P), .B(q0), .C(y1), .Y(y0));
nand3 U6 (.A(P), .B(q1), .C(y0), .Y(y1));
nand2 U7 (.A(q0), .B(q1), .Y(cd));
endmodule
module nand2(
input wire A, B,
output wire Y
);
assign #1 Y = ~(A & B);
endmodule
module nand3(
input wire A, B, C,
output wire Y
);
assign #1 Y = ~(A & B & C);
endmodule
Обратите внимание, что у логических элементов обязательно должна быть ненулевая задержка, а схема требует начальной установки. В железе (если кто то попробует сделать эту схему на ПЛИС или россыпи) начальная установка не требуется.
А теперь займемся реверс-инжинирингом, чтобы понять, как получить схему счетного триггера с помощью сетей Петри. Выберем произвольную начальную расстановку значений на выходах элементов (можно взять из моделирования, или придумать самим):
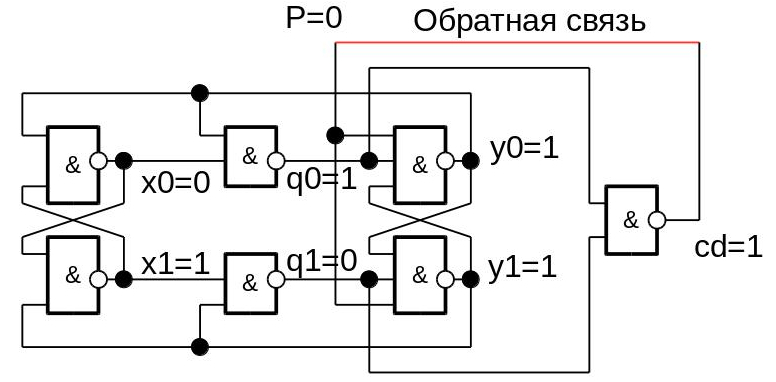
Поскольку P=cd, то значение P в следующий момент времени должно измениться на 1. Построим граф, в вершинах которого будут переменные, а ребра – направление переключения переменных. Переменные пометим знаком +, если они переключились из 0 в 1, а знаком минус, если они переключились из 1 в 0. Граф введем в редакторе Workcraft ( можно скачать бесплатно с сайта http://www.workcraft.org. Выбираем меню File — Create work — Signal Transition Graph, и вводим граф). Начальное переключение сигнала P из 0 в 1 (т.е. P+) пометим входящей срелкой с кружком (токеном). Получится граф:
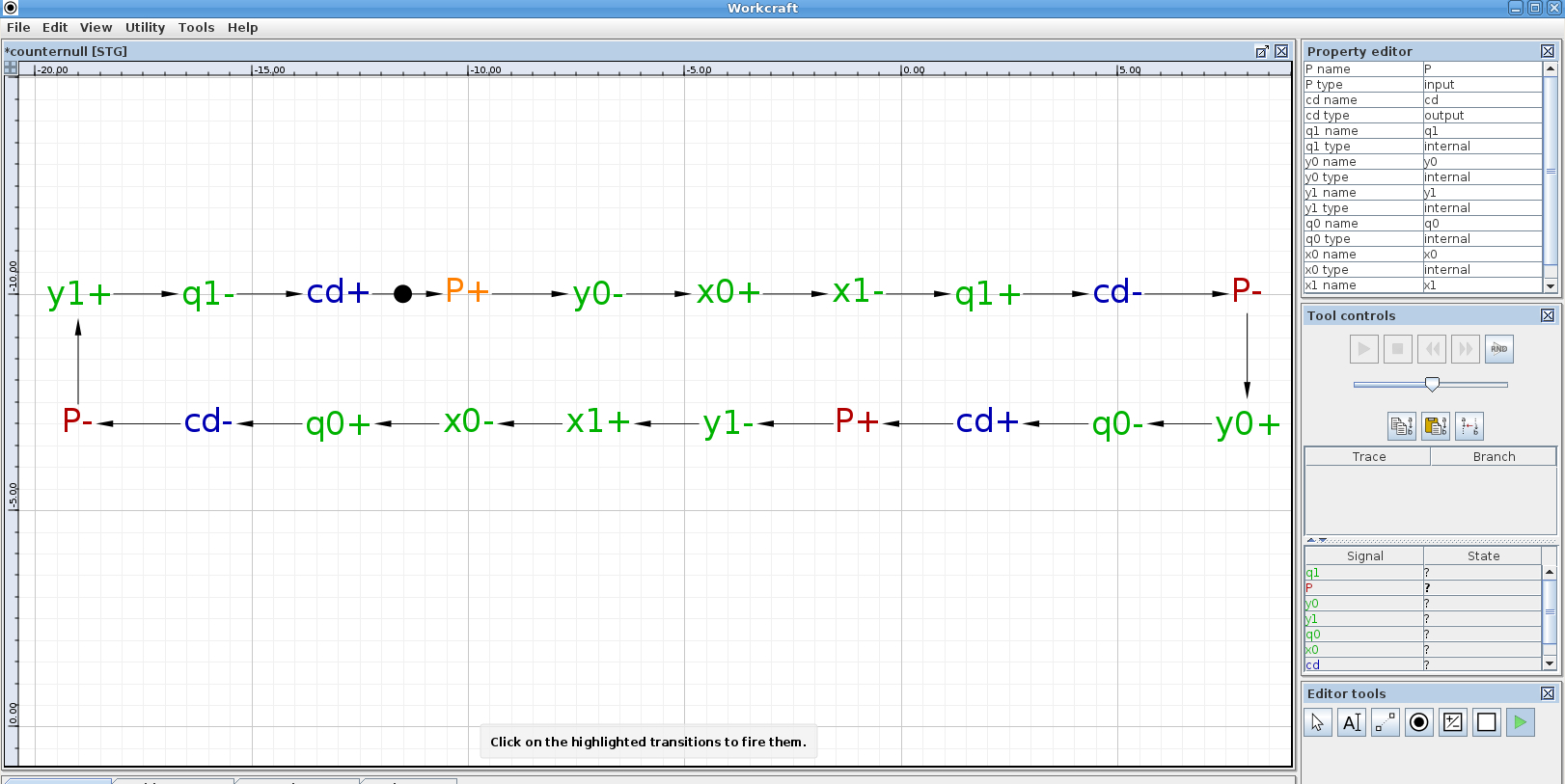
После переключения P в 1 следует переключение сигнала y0 в 0, затем x0 в 1, и т.д., пока не вернемся к началу. Как видно из графа, выходные переменные {q1,q0} переключаются в цикле 10-11-01-11-10-11 и т.д., что соответствует работе счетного триггера. Можно включить режим симулятора работы сети Петри, для этого надо нажать на иконку зеленого треугольника в правом нижнем окне Editor Tools, а затем запустить симуляцию в появившемся выше окне Tool Controls.
Следующий шаг – синтез графа в Petrify. Выбираем в меню Tools – Synthesis – Complex gate synthesis [Petrify], и получаем лог:
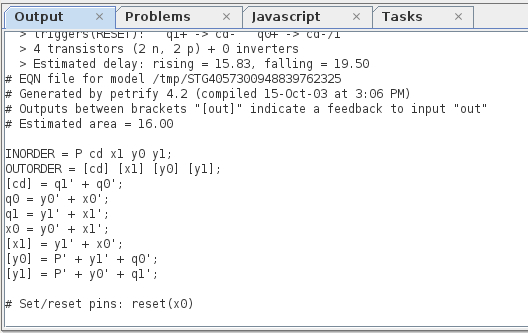
Синтез прошел успешно (что означает, что схема является
Из графа становится очевидно, что работоспособность счетного триггера не зависит от задержек: в какое бы место схемы Вы не добавили задержку, это лишь замедлит его работу, но не изменит порядок переключения элементов и не нарушит логику работы схемы.
Описанные процедуры (в порядке: от графа к схеме) позволяют синтезировать и проверять на самосинхронность только схемы защелок, триггеров, счетчиков, либо произвольных контроллеров, чье поведение описывается сетью Петри, содержащей не более 50 переменных. Более сложные схемы приведенным способом разрабатывать нельзя (необходимо использовать другие подходы к проектированию). Но для изучения основ разработки самосинхронных схем, рассмотренный пример счетного триггера (а так же туториалы из дистрибутива workcraft) – самое то. Заинтересовавшимся теорией рекомендую почитать учебник по сетям Петри и самосинхронным схемам: Мараховский В. Б., Розенблюм Л. Я., Яковлев А. В. Моделирование параллельных процессов. Сети Петри, а так же изучить материал на сайте разработчиков workcraft.
Комментарии (17)

andy_p
20.07.2016 21:23Можно еще это почитать:
Л. П. Плеханов Основы самосинхронных электронных схем.
Л. П. Плеханов- дядя мой.

UA3MQJ
21.07.2016 11:19+2Я тут одно время экспериментировал с самосинхронными схемами с их последующим синтезом в ПЛИС Altera. Первой целью было ввести к 1 и 0 еще одно состояние, которое ни то и ни другое. Например Z. Но в симуляции если это все и работает, то в железе нет. Очень много «зарубает» оптимизатор синтезатора. В итоге, пришлось выяснить особые команды для синтезатора, чтобы не зарубал. Можно насильно создавать асинхронные RS триггеры и на них строить все. После всяческих экспериментов пришел к своему решению, которое оказалось велосипедом. Велосипед называется NCL (null conversion logic). Реализована простейшая логика (и, или, не). Вот уже пару лет неспешно это прорабатываю. Может быть тоже статейку напишу.
Спасибо за статью
Khort
21.07.2016 11:43+1А как удалось организовать RS-триггеры на ПЛИС?
Я в свое время искал, и не нашел таких ПЛИС, у которых триггеры имеют асинхронный сброс и установку. Задействовать два LUT внутри одного LAB тоже не получается — внутри LAB нет роутинга в обратную сторону. В результате я пришел к тому, что RS триггер (или сразу С-элемент) можно построить только на двух LAB, что очень расточительно.
По поводу NCL, я лично отношусь к этой технике скептически, поскольку там каждый элемент логического базиса содержит в себе защелку. Т.е. размер схемы получается чудовщиный, а эффект тот же, что и у самосинхронных. Но это — на вкус и цвет
Chinook
21.07.2016 12:38> внутри LAB нет роутинга в обратную сторону
Я может чего не понял, но разве вот это не оно:
The LAB local interconnect can drive LEs within the same LAB. The LAB
local interconnect is driven by column and row interconnects and LE
outputs within the same LAB.
Khort
21.07.2016 12:43В LAB делают обратную связь, но только с выхода D-триггера. А для создания RS триггера на двух LUT требуются обратные связи с выходов именно LUT, а не D-триггера.

Chinook
21.07.2016 12:49Да нет же, на схеме LE сигнал на local routing выдаётся с выхода LUT или регистра через мультиплексор.

Chinook
21.07.2016 13:04А-а, вы наверное имеете в виду register feedback. Он действительно идёт с выхода регистра на вход LUT только внутри того же LE. Но есть ещё local routing: с выхода регистра или LUT одного LE на вход любого LE в том же LAB.

Khort
21.07.2016 13:28Именно. Получается, что на одну самосинхронную защелку нужно 2 LAB (c использованием local interconnect), а для полноценного самосинхронного Flip-Flop триггера — уже 4 LAB. С-элемент тоже потребует 3-4 LAB с дополнительным local interconnect. Об этом я и писал выше.
В конечном счете, и триггеры и С-элементы — только маленькие винтики в схеме, и если так расточительно тратить local interconnect, то скольконибудь серьезная схема может не влезть в ПЛИС. В идеале хочется обойтись вообще без local interconnect, и это было бы возможно с D-триггером с асинхронным сбросом и установкой (который можно превратить в RS-защелку, подав на клоковый вход константу). Проблема в том, что асинхронные сброс/установка в ПЛИС как правило глобальные, а для асинхронных схем сигналы Set/Reset каждого триггера должна формировать локальная логика. Выходит, снова упираемся в ресурсы ПЛИС — глобальных линий сброса/установки очень мало. Но, надо поэкспериментировать.
Chinook
21.07.2016 13:53+1Пардон, но здесь похоже путаница в терминологии. Давайте проясним, у Альтеры:
LE – логический элемент, содержит LUT и DFF,
LAB (logic array block) – группа из 10-16 LE,
local interconnect – интерконнект внутри LAB, его хватит чтобы завернуть на вход по одному выходу с каждого LE и он не является критичным ресурсом.
MultiTrack interconnect (Row and Column) – основной интерконнект внутри чипа. Это уже ограниченный ресурс.
В этой терминологии утверждение, что на защёлку нужно 2 LAB и т. п. является несколько преувеличенным. То же касается local interconnect – тратить его совсем не расточительно, раз уж используются LE.
Насчёт асинхронные сброс/установка глобальные, не совсем так. Опять же для Альтеры они просто общие для всех LE одного LAB. Сбросов обычно 2 на LAB.

Chinook
21.07.2016 12:44Забыл ещё вот это:
> не нашел таких ПЛИС, у которых триггеры имеют асинхронный сброс и установку
Ну MAXII имеет асинхронную загрузку, которая может использоваться как асинхронная установка. Но MAXII, вероятно, не то, что вам нужно.

UA3MQJ
21.07.2016 12:51Так там одна макроячейка все это и содержит: триггер с разными типами входов. Надо использовать lov level primitives. Я даже немного про это написал тут.
По поводу NCL, я лично отношусь к этой технике скептически
Надо на практике пробовать. Там видно будет. Но хотя бы в надежности есть какая-то уверенность, т.к. сигнал получается дифференциальный. А с одним сигналом — нет гарантии, что его значение верное, да плюс метастабильность…
Chinook
21.07.2016 12:57Примитив может содержать все нужные входы, а вот аппаратная реализация – нет. Тогда синтез всё-равно делает регистр из нескольких LUT.

UA3MQJ
21.07.2016 13:09Тут надо глядеть отчет синтезатора и схему, которую создает синтезатор. Плюс, нужно обязательно задавать опции синтезатора, чтобы он не поудалял все. Он же стремится сократить и создать оптимальную синхронную схему, а нам нужно все наоборот

Chinook
21.07.2016 13:18Если использовать примитив, синтезатор сделает всё как надо. Он знает где и как он делает регистры из LUT. Вот если попытаться описать такую логику вручную, тогда да.


andy_p
Тогда уж Варшавского надо читать.
Khort
Трудно не согласиться. Но у Варшавского не простых книг, где бы начиналось с «азов». Без серьезной математической подготовки Варшавский вообще не читабелен, на мой взгляд. А вот учебник, что я присоветовал в конце — весьма и весьма читабелен.