Нужно ли вам читать этот текст?
Давайте проверим. Прочтите следующее:
Тригонометрическим рядом Фурье функции? называют функциональный ряд вида
где
Страшно, но всё же хочется понять, что это значит?
Значит, вам под кат. Постараюсь формул не использовать.
Мотивация
По моему глубокому убеждению, к математике можно подходить на двух уровнях: большинство людей её видит (им её именно так и преподают) как набор значков и правил операций над значками, что приводит к широким массам людей, математикой травмированных. А можно попытаться передать смысл и идеи, не особо заостряясь на значках. Лично я неспособен к синтаксическому подходу, я в цепи из двух формул обязательно потеряю какой-нибудь минус, что не мешает мне достаточно успешно считаться математиком. Просто у меня в голове графический ускоритель.
Я уже приводил цитату Фейнмана о том, как именно он читал все уравнения, что ему приходилось:
Actually, there was a certain amount of genuine quality to my guesses. I had a scheme, which I still use today when somebody is explaining
something that I'm trying to understand: I keep making up examples. For instance, the mathematicians would come in with a terrific theorem, and they're all excited. As they're telling me the conditions of the theorem, I construct something which fits all the conditions. You know, you have a set (one ball) — disjoint (two balls). Then the balls turn colors, grow hairs, or whatever, in my head as they put more conditions on. Finally they state the theorem, which is some dumb thing about the ball which isn't true for my hairy green ball thing, so I say, «False!»
И при подготовке этого текста я наткнулся на замечательный доклад Анри Пуанкаре, который, пожалуй, был величайшим математиком конца девятнадцатого и начала двадцатого столетия. Он указывал, что даже в такой абстрактной науке, как математика, следует культивировать интуитивные понятия, например, понятие прямолинейности, хотя интуиция и должна проверяться формальными доказательствами.
Его доклад озаглавлен «Du role de l'intuition et de la logique en mathematiques», на французском можно прочитать тут, английский перевод доступен здесь. Крайне рекомендую интересующимся математикой, читается на одном дыхании.
Update: Вот тут лежит перевод на русский язык.
К сожалению, передавать интуицию очень сложно, но я попытаюсь, так как выгода от переданной интуиции несравнимо выше от выгоды передачи просто значков.
На что я опираюсь в этом тексте
Перво-наперво нужно знать, что такое вектор, хотя бы на уровне «стрелочка». Ну и представлять, что стрелочки можно рисовать в существенно большем количестве размерностей, нежели 2 или 3. Ну и что хранить вектор можно в std::vector.
Затем центральным понятием является скалярное произведение.
На пальцах скалярное произведение можно представлять как меру того, насколько один вектор похож на другой. То есть, это операция, которая на вход берёт два вектора, на выход даёт число. Нормирование данных это уже детали, пока не очень нужные. Поэтому если у меня есть две стрелочки единичной длины, то скалярное произведение равно единице, если стрелочки совпадают, нулю, если они ортогональны и минус единице, если они противонаправлены.
Лирическое отступление
Это не просто лирика, это пример, который на первый взгляд не связан с темой разговора, но на самом деле является его сутью. Хотите понимать дальше — понимайте пример. Что неясно, задавайте вопросы.
Давайте на минуту рассмотрим крайне практическую задачу: у меня есть неспешный робот, и он должен знать, где он находится. Система навигации должна быть пассивной. Я люблю крайне дубовые решения, поэтому я ставлю на моего робота два микрофона (как уши у человека). Затем у меня есть маяк (на самом деле несколько, но давайте про один), который проигрывает в цикле некоторый (моно) звук. Например, вот такой:

Это просто сухие щелчки, положим для простоты один щелчок в секунду.
«Уши» робота находятся на разном расстоянии от маяка, а звук распространяется неспешно, поэтому каждый из двух микрофонов запишет плюс-минус один и тот же сигнал, но с небольшой задержкой один относительно другого. Я не ищу легких путей, поэтому у меня не лабораторные условия. Вот, например, как выглядит запись в течение нескольких секунд:
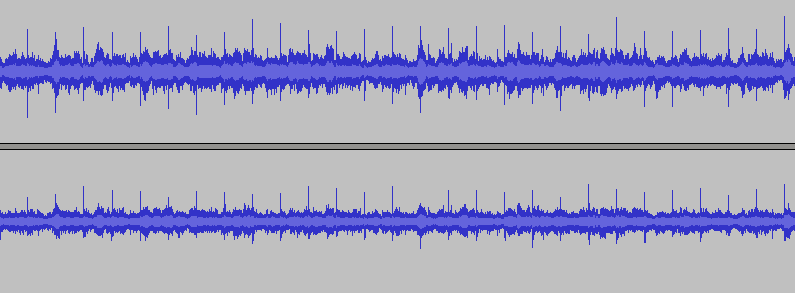
Два канала по количеству ушей, высокий уровень шума (играет музыка). На записи видно регулярные всплески сухих щелчков, но напрямую искать их в сигнале крайне непросто, иногда музыка бывает даже громче щелчков.
Как мне убрать фоновый шум? Напоминаю, робот у меня совсем неспешный. Самый дубовый способ — это записать час звука, затем порезать его на 3600 кусков в одну секунду длиной (у меня один щелчок в секунду), и взять среднее между всеми этими кусочками записи.
Получится нечто вот такое:
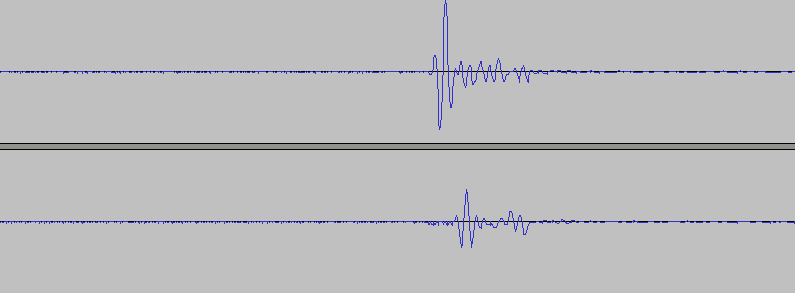
Пики щелчков приходятся в каждом из 3600 кусков на одно и то же место, а остальной шум размазан более-менее равномерно по всей длине, в итоге шум уходит. К слову сказать, маяков у меня несколько, никакой синхронизации между ними нет, а ушей только два. И именно так я и разделяю сигналы с маяков: один маяк щёлкает три раза в секунду, другой пять, третий семь. (Очень важно) Порезав один и тот же сигнал на кусочки в 1/3, в 1/5 или в 1/7 секунды, я получу сигнал именно с нужного маяка!
Итак, теперь мне нужно понять, как один сигнал сдвинут относительно другого. Мне абсолютно всё равно, в каком именно месте записи у меня пик, мне нужен сдвиг одного канала относительно другого.
Для начала давайте поймём, как я вообще представляю этот сигнал в памяти машины. Я пишу обычный wav с частотой дискретизации 44100Гц. Длина записи одна секунда, таким образом, у меня есть просто два массива (вектора!) вещественных чисел со 44100 элементами.
Фиксируем один вектор, а второй 44100 раз циклически сдвинем вправо. (Очень важно) Посчитаем 44100 скалярных произведения и возьмём тот сдвиг, при котором это скалярное произвдение максимально. То есть, именно этот сдвиг максимизирует похожесть двух сигналов. Поздравляю вас, вы только что посчитали взаимнокорреляционную функцию!
Update: хороший комментарий с иллюстрацией.
А теперь давайте считать ряд Фурье в уме
Предыдущая секция очень важна, но пока давайте её отложим и попробуем посчитать на пальцах простой ряд Фурье.
В качестве примера давайте возьмём простой квадратный сигнал, так любимый в электронике. Графики я рисую в sage.
def square_wave(t): return (sgn(sin(t))+1)/2
t = var('t')
plot(square_wave(t), (t, -10*pi, 10*pi),figsize=(10,2))
Это простой периодический сигнал с периодом в 2 pi. Половину времени он равен нулю, половину времени равен единице. Давайте считать коэффициенты ряда Фурье (см. начало статьи).
Нулевая частота
Коэффициент a0 — это просто среднее сигнала, очевидно, что он равен половине. Как считать a1 и b1?
Первая частота
А вот тут я предлагаю нарисовать один период нашего сигнала, но на сей раз не в обычной декартовой системе координат, но в полярной. Итого у нас угол идёт от нуля до двух пи, и мы получим следующую картинку:
parametric_plot((cos(t)*square_wave(t), sin(t)*square_wave(t)), (t, 0, 2*pi))
Почему в полярной системе? Очень просто. Как преобразуются полярные координаты точки (r,alpha) в декартовы?
x = r cos(alpha),
y = r sin(alpha).
А что у нас стоит под знаком интеграла в формуле для a1 и b1? Правильно, f sin(t) и f cos(t). Осталось проинтегрировать. Как это сделать в уме? Представьте, что у вас это не математический график, а отрезок проволоки. Давайте найдём его центр тяжести. Очевидно, что он будет лежать на оси ординат примерно в центре нашей дуги (на самом деле, на расстоянии 2/pi от центра, ну да это не суть, давайте назовём это расстояние A):
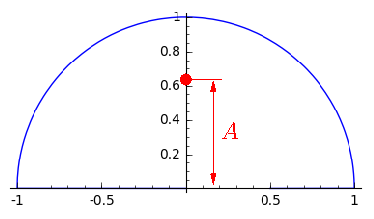
Координаты красной точки (центра тяжести графика) и есть нужные нам интегралы (с точностью до умножения на константу, ну да это не суть). Кстати, а можете сказать, почему именно так?
Итого a1 = 0, b1 = A.
Вторая частота
Что до a2 и b2? Давайте снова делать полярный график, «наматывая» наш обычный график вокруг нуля. Единственное, что теперь мы будем наматывать, делая два оборота.
Первый оборот:
parametric_plot((cos(2*t)*square_wave(t), sin(2*t)*square_wave(t)), (t, 0, pi))
parametric_plot((cos(2*t)*square_wave(t), sin(2*t)*square_wave(t)), (t, pi, 2*pi))Второй оборот очевидно будет пустым, наш квадратный сигнал в этот момент равен нулю:

Центр масс первого + второго графиков лежит, очевидно, в нуле. Таким образом, a2=0, b2=0.
Третья частота
Теперь намотаем вокруг нуля один период нашей функции три раза, для наглядности я показываю три витка на раздельных графиках:
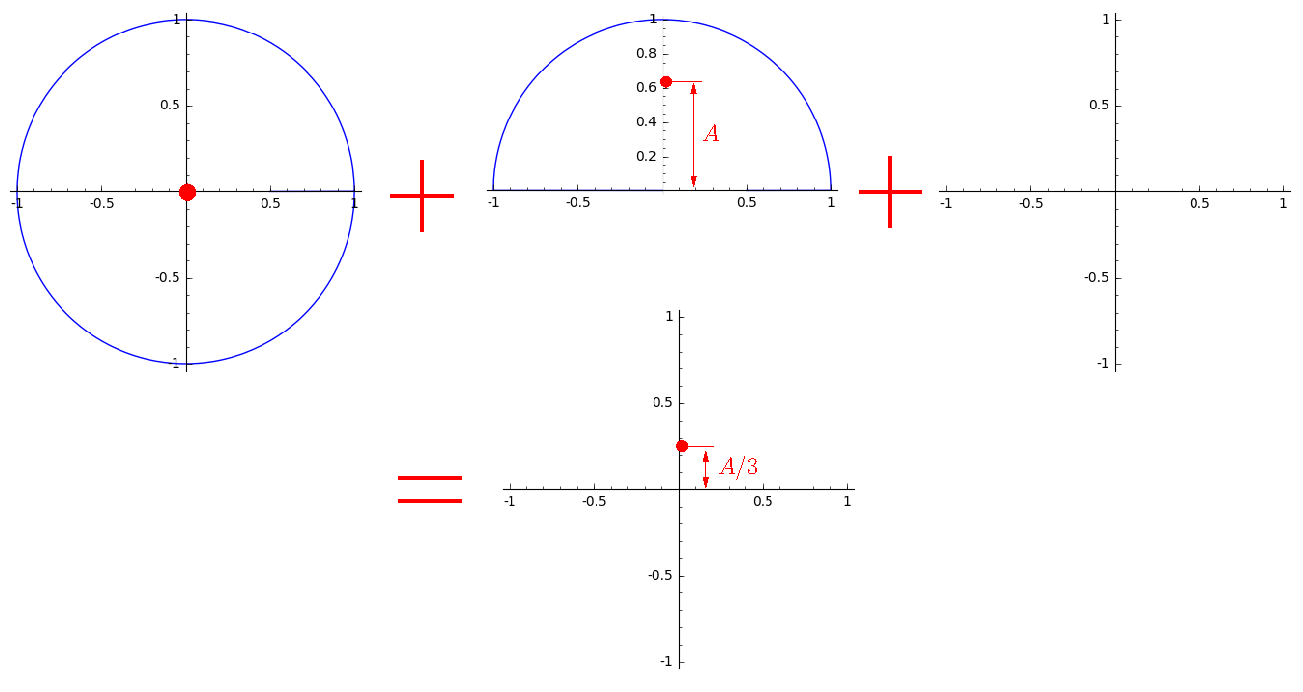
Первый виток заполняет полностью нашу окружность, второй наполовину, а третий пуст. Если один полный виток весит один килограмм, то мы имеем один килограмм в нуле и полкило на расстоянии A от нуля. Итого, центр тяжести будет на расстоянии A/3 от нуля.
a3 = 0
b3 = A/3
Более высокие частоты
Что будет с четвёртой частотой? Два заполненных витка и два пустых, центр в нуле. И так для всех чётных.
Что будет с пятой частотой? Два заполненных, два пустых и один полувиток. Итого центр тяжести на оси ординат на расстоянии A/5 от нуля.
Подводим итог
Если посмотреть ещё раз, как мы считаем интегралы, то станет понятно, что между нашим сигналом (квадратной волной) и функциями cos(nx), sin(nx) мы ищем скалярные произведения. То есть, мы смотрим, насколько наш сигнал похож на cos(nx) и насколько он похож на sin(nx). Наматывая определённое количество раз график (периодической!) функции вокруг нуля, мы гасим все частоты, кроме текущей.
Полярный угол нашего центра тяжести говорит, насколько сигнал похож на соответствующий синус или насколько он похож на соответствующий косинус. А расстояние, на котором находится центр тяжести, говорит о силе их вклада в формирование нашего сигнала.
Итого наш ряд равен f(x) = 1/2 + 2/pi sin(x) + 2/(3 pi) sin(3x) + 2/(5 pi) sin(5x) +…
Домашнее задание
1) Вы поняли связь между примером с роботом и квадратной волной?
2) А как связан ряд Фурье с преобразованием Фурье?
Комментарии (97)

awfun
25.08.2016 20:09+3Когда первый раз увидел аналогию с векторами, тоже очень порадовался простоте:
1. Там и там базис может быть бесконечномерным
2. Там и там есть произведение: в векторах покоординатное, в Фурье как результат вычисления интеграла (как его вычислять — другое дело, на понимании это не отражается)
3. Через произведение можно определить разложение по базису
Что меня не радует в такой аналогии — ряд из векторов сходится везде, а ряд из функций только при определенных значениях аргумента. А при других — разойтись в бесконечность или сойтись к какой-то третьей функции. Можно ли это объяснить на векторах?Sayonji
25.08.2016 22:36+2ряд из векторов сходится везде
Что вы имеете в виду под этим? По аналогии с функциями, ряд из векторов тоже «может» сходиться в каких-то компонентах, а в каких-то расходиться. Например,
сумма от единицы до бесконечности (0, 1/n, 1/2^n) равна (0, +inf, 1).
awfun
26.08.2016 11:11Имею в виду, что если я беру базисом вектора
x1 = {1; 0; 0...}
x2 = {0; 1; 0...}
x3 =…
И раскладываю какой-то вектор по этому базису: {a; b; c; ..} = a * x1 + b * x2 +…
То левая часть равна правой всегда, т.к. нет зависимости от переменных.
В примере из статьи: f(x) = 1/2 + 2/pi sin(x) +…
Равенство верно для некоторого множества иксов, а для другого может быть неверно.mayorovp
26.08.2016 11:15В примере из статьи равенство будет верно для всех иксов если функция f является
гладкой и периодической с периодом 2?удовлетворяет условиям теоремы.

popolznev
26.08.2016 09:08+4Это не аналогия. Вектор — это то, что можно умножать на число и складывать с другими векторами (в том же векторном пространстве). Функции можно умножать на числа и складывать с другими функциями. Так что функция — это частный случай вектора.
splav_asv
26.08.2016 11:04Более того, число — частный случай функции.

popolznev
26.08.2016 11:43-2Нет, это не так.

haqreu
26.08.2016 12:10Слушайте, давайте не будем разводить флейма, но мне кажется, что вы несколько поспешно это сказали.
mayorovp
26.08.2016 13:33Числу можно поставить в соответствие функцию ноля аргументов или постоянную функцию на любом множестве — но само число от этого функцией не станет. У них разные определения.

haqreu
26.08.2016 13:45Если вы ещё можете мне определить, что такое число, не прибегая к теории категорий, будет вообще отлично. Давайте не будем разводить флейм, ладно?

Halt
28.08.2016 11:34Если говорить о натуральных числах, то их можно описать используя только базовые аксиомы теории множеств. Остальные выводятся по определению. Но там в процессе определения все еще присутствует фраза «ставить в соответствие» что в общем-то подразумевает наличие понятия морфизма.

haqreu
28.08.2016 12:42А что запрещает числу быть функцией?

Halt
28.08.2016 12:58Ничто не запрещает :) Не далее как вчера читал доклад по основам лямбда-исчисления, где числа вполне себе представляются функциями.
На мой взгляд, понятие множества более интуитивно, чем функция.
haqreu
28.08.2016 13:22В лямбда-исчислении напряги с вещественными числами, ну да не суть. Я и говорю, что разговор долгий и конечный ответ неочевиден.

barkalov
26.08.2016 13:47«Натуральному числу 5 можно поставить в соответствие действительное число 5.0 — но само натуральное число от этого действительным не станет. У них разные определения.»

popolznev
26.08.2016 14:56-3Давайте не будем ничего разводить. Я знаю что говорю.

haqreu
26.08.2016 15:03-2Что характерно, я тоже стараюсь не говорить того, чего не знаю.
Я лишь вам пытаюсь сказать, что не всё так быстро, как вы заявляете. Это будет длинным обсуждением, которое не касается темы текущей статьи. Ваша категоричность на зыбкой почве неопределённости удручает.
popolznev
26.08.2016 15:11-3Я не «заявлял, что всё быстро», а отреагировал на конкретное ложное утверждение, которое было написано в ответ на мой комментарий. Обратите внимание, что я и не обсуждаю вопроса, который вам так не хочется обсуждать.

haqreu
26.08.2016 15:17-3Вы понимаете, что определения понятий, которые вы имеете в вашей голове, могут не совпадать с, например, моими? И именно тут мы приходим к излишней категоричности и поспешности вашего заявления о ложности.

popolznev
26.08.2016 15:32-1Вы понимаете, что определения понятий, которые вы имеете в вашей голове, могут не совпадать с, например, моими?
Разумеется.
И именно тут мы приходим к излишней категоричности и поспешности вашего заявления о ложности.
Не следует.

kalobyte
25.08.2016 23:55+4что-то у меня куда-то пропали кнопки в редакторе
теперь цитату не воткнуть
короче
прочитал
нихера не понял
вот я еле осилил пту в 27 лет, в 31 пошел в быдловуз, но не осилил ничего из тамошнего бреда
меня вот интересует не абстгактный матан, а например как написать модулятор сигнала на с#
вот что забавно
«Порезав один и тот же сигнал на кусочки в 1/3, в 1/5 или в 1/7 секунды, я получу сигнал именно с нужного маяка!»
а откуда _я_ это должен узнать? ты просто преподносиш это как факт, типа делай так и получиш вот так
«Фиксируем один вектор, а второй 44100 раз циклически сдвинем вправо. „
а почему вправо? и что значит сдвигаем? ты имееш в виду операцию сдвига вправо? как это выглядит в коде?
“А теперь давайте считать ряд Фурье в уме»
зачем его считать, что такое ряд фурье в реальности? зачем мне его считать?
ну вот ты взял прямоугольный сигнал и что должны получить в конце? какой с этого профит?
«А вот тут я предлагаю нарисовать один период нашего сигнала, но на сей раз не в обычной декартовой системе координат, но в полярной.»
зачем???7 если прямоугольник мне еще понятен и я могу себе представить образ в голове прямоугольного сигнала, то зачем мне еще какие-то там координаты? какой профит я получу?
с этого момента я дальше читал просто набор букв и непонятных картинок
ты в sdr что-то понимаеш? можеш написать статью, как сделать амплитудный модулятор и демодулятор на c#? пусть даже на низких частотах звуковой карты
вот хорошая статья базовая, тут все понятно и наглядно с картинками
http://we.easyelectronics.ru/teplofizik/rabota-s-sdr-svistkami-na-c-rtl2832.html

lectricas
26.08.2016 00:00Странный текст, не осилил. Сначала вы писали все просто а потом как задвинули:
Для начала давайте поймём, как я вообще предста....(Очень важно) Посчитаем 44100 скалярных произведения и возьмём тот сдвиг, при котором это скалярное произвдение максимально.
А дальше вообще:
Коэффициент a0 — это просто среднее сигнала
я посмотрел на формулу и не понял, почему это среднее.
В общем матан это сложно и с наскока не получиться. Пойду курсеру посмотрю что ли.
haqreu
26.08.2016 00:02Если вы не разобрались, то это вполне нормально. Но если вы хотите понять, то задавайте вполне конкретные вопросы. Пока я их не вижу, а следовательно, не понимаю, зачем вы написали этот комментарий.

rafuck
26.08.2016 01:00+1Ну, в частности он спросил, почему константная компонента в разложении представленного сигнала равна 1/2 :)

haqreu
26.08.2016 01:07-3Обычно в конце вопроса ставится вопросительный знак. Ну или вопрос оформляется как просьба. Здесь я вижу констатацию факта с неясными для меня целями.
Но вообще интеграл — это площадь подграфика. Грубо говоря, это среднее значение по графику, помноженное на длину графика.
pacahon
26.08.2016 12:00А можно разъяснить, почему площадь под графиком равна pi/2? Написано, что период 2*pi, половину времени сигнал равен 1, значит площадь будет pi.

haqreu
26.08.2016 12:05+1А, ну это мой ляп, интеграл, конечно, равен ?. Среднее значение сигнала 1/2, множим на длину 2?, получаем ?. Таким образом, a0=1
Я забыл, что в формуле ряда Фурье стоит a0/2 в коэффициенте, а не просто a0. Я ж говорю, что формулами пользоваться не умею. Понимаю, что нужно сигнал поднять на 1/2, чтобы он от 0 до 1 был, ну вот и славно.
pacahon
26.08.2016 12:55Спасибо. А какая главная мотивация наличия 2 микрофонов? Это как раз "недубовый" способ избавиться от шума и выделить полезный сигнал?

haqreu
26.08.2016 13:44Нет, мне нужно два микрофона, чтобы знать, где находится источник звука, ровно как вы локализуете звук двумя ушами. С монозвуком это сделать сложно :)
diafour
26.08.2016 12:10+4Ну и представлять, что стрелочки можно рисовать в существенно большем количестве размерностей, нежели 2 или 3.
На пальцах скалярное произведение можно представлять как меру того, насколько один вектор похож на другой.
Секундный сэмпл — это вектор размерностью 44100.
Попробую соорудить аналогию для иллюстрации процесса:
Пусть есть две строки с пробелами и словом где-то между пробелами (пробелы ест парсер, пусть будет минус), например,
s1 = "----------Slovo---"
s2 = "-------Slovo------"
Теперь примем, что строки s1 и s2 — это вектора размерностью 18, а значения координат это ASCII коды символов. Дальше из s2 получим 18 векторов с помощью циклического сдвига:
s [0] = "-------Slovo------"
s [1] = "--------Slovo-----"
s [2] = "---------Slovo----"
s [3] = "----------Slovo---"
s [4] = "-----------Slovo--"
...
s [8] = "vo-------------Slo"
...
s[17] = "------Slovo-------"
s[18] = "-------Slovo------" == s[0]
Теперь остаётся подсчитать 18 раз скалярное произведение строки s1 с каждым из полученных векторов и запомнить тот вектор и его индекс, где будет наибольшее скалярное произведение. Полученный индекс будет сдвигом «Slovo» в строке s2 относительно строки s1.

REPISOT
26.08.2016 00:18-1квадратный сигнал, так любимый в электронике
Квадратные сигналы у нас обсуждают только «специалисты» из Госду… мы.
А в ЦОС и Теории сигналов и цепей это — прямоугольный сигнал. В данном случае — Меандр
haqreu
26.08.2016 00:20Да, я использовал кальку со вполне стандартного термина «square wave». Но при этом любопытно, что вместо того, чтобы просто вежливо предложить русский аналог, вы начинаете хамить. По-моему, зря.

REPISOT
26.08.2016 06:16+3Претендовать на научность и при этом — плавать в базовых терминах — высшее неуважение к читателям. Да еще и ссылка
так любимый в электронике
это просто оскорбление всех электронщиков.
Особенно плохо, что если кто-то начинающий или просто любитель поведется на ваш «tutorial», то он нахватает левых терминов.
И тут неуместно выражение «посчитаем в уме».
«Вручную», «без компьютера» — может быть. Но то, что описано в статье — это не «в уме»
И не надо ссылаться на перевод. Это еще больший косяк чем невежество. Это пренебрежение.
Увидел незнакомый термин, «но слова то, вроде знакомые, пусть будет квадратный сигнал. и так сойдет»
haqreu
26.08.2016 09:14-2А что в этом подсчёте не делается в уме? То, что я был вынужден нарисовать картинки вместо телепатической трансляции? Или там такие сложные картинки, что прямо не представить, что у нас точка ездит по окружности, половину времени рисует, половину нет?

tarkvin_aktus
26.08.2016 00:48+1«что приводит к широким массам людей, математикой травмированных»
Тут вы точно правы.
Я студент, который только весной закончил 4ый курс матана. Все формулы разумеется мне знакомы, я решал это. Конечно сей коммент может говорить о моей «одарённости» и «способностях», но к концу статьи у меня задёргался глаз и чуть не пошла пена изо рта.
haqreu
26.08.2016 00:50+1Подобного рода тексты нельзя просто читать, возьмите карандаш и попытайтесь воспроизвести каждую операцию самостоятельно. А затем понять, почему была сделана именно это операция, а не иная другая. Не получится понять — задавайте вопрос.

dzobnin
26.08.2016 19:19+1А я думал, что статьи пишут, чтобы их понимали, а не чтобы потом в комментах объяснять.

haqreu
26.08.2016 20:01Один и тот же текст не будет понятен всем людям. Почему вы предлагаете не пользоваться возможностью задать вопрос, раз уж такая имеется? Я вас уверяю, я нередко пишу вопросы авторам книг. И получаю ответы, что характерно…

dzobnin
27.08.2016 02:18+1Ваш сумбурный текст будет понятен только тем, кто и так понимал эту тему. Тем, кто тему не понимал, статья не поможет от слова совсем :) То есть статья не нужна.
С тем же успехом вы могли написать: «Читайте функан, и пишите вопросы в комментах».
Vjatcheslav3345
27.08.2016 12:03+1Мне, кстати, так и советовал научрук диссер писать — он говорил — найди баланс между понятностью, с опорой на то, что знает даже неспециалист в этом вопросе (но не разжевывая, что Солнышко — оно желтое) и предельной краткостью (отожмём текст досуха на отжималке от бабушкиной стирмашинке, но не так, чтобы его порвать на лоскутья) и вот тогда, канатаходцем пройдя меж крайностями, придав стиль тексту, ты и получишь требуемое; если в процессе написания ты ещё и чувствуешь удовольствие — значит двигаешься в нужном направлении: чего желаю и Вам, ибо идеи интересные, осталось чуть поправить их реализацию.

haqreu
27.08.2016 12:13-1Да, как-то так, спасибо за хорошо сформулированный рецепт. У диссертации есть только один минус — она пишется с малым количеством итераций (чаще всего вообще в один проход). А получить хорошее объяснение можно лишь многократно отработав его на разных людях. Что, в частности, я и делаю на этом ресурсе (и не только тут). И если отфильтровать рассказы о том, какой я мудак и что мои тексты не нужны, то в комментариях я почерпнул немало ценного. А там потихоньку и книга скомпилируется.

julie
26.08.2016 06:31Я пишу обычный wav с частотой дискретизации 44100Гц. Длина записи одна секунда, таким образом, у меня есть просто два массива (вектора!) вещественных чисел со 44100 элементами.
откуда тут второй вектор?

chianti
26.08.2016 09:05Мне, как человеку любящему математику (хотя и, на самом деле, слабо ею владеющему), статья понравилась. Единственное, что смутило:
— в примере с роботом, он что стоит на одном месте и вообще не двигается? Зачем ему тогда система навигации? Если же двигается, то, мне кажется, такая простая фильтрация работать не будет.
— после анализа прямоугольных сигналов статья закончилась и остается совершенно непонятно, как теперь посчитать ряд фурье «в уме», например, для пилообразного сигнала, в котором встречаются и отрицательные коэффициенты.
Все таки, мне кажется, гораздо более универсальным подходом будет разобраться в интегрировании, пусть даже и численными методами.
haqreu
26.08.2016 09:39Робот движется, но может позволить себе остановиться на десять секунд, этого на самом деле вполне достаточно. Я в примере использовал час, чтобы было понятнее, почему уйдёт шум.
Для пилообразного сигнала ряд в уме считать чуть сложнее, но тоже возможно: вам даже не надо представлять теперь витки отдельно, т.к. достаточно представить себе спираль (cos(n*t)*t, sin(n*t)*t).
Вполне очевидно, что ни влево, ни вправо она не перевесит, а её центр тяжести будет лежать на оси ординат, в отрицательной половине. И тем ближе к нулю, чем выше частота. Частоты присутствуют все.
так что там должно быть что-то навроде -sin(x) — sin(2x)/2 — sin(3x)/3…
Но при этом вы, видимо, не поняли, что я вовсе не призываю считать в уме все возможные ряды. Один простой посчитали — уже хорошо. Это всё нужно просто для создания ментальной картинки, которая поможет дебажить формулы, в которых вы однажды неминуемо ошибётесь.
Я в самом начале сказал, что цепочку формул сам не могу написать корректно. Ну да и бог с ней, пусть будет некорректно. Зато у меня есть возможность взять самую последнюю (например, просто прочитав в книге) и применить к ней некоторое количество sanity checks путём простого наделения смыслом разных значков. И весьма вероятно, что я увижу ошибку в выводе.
GarryC
26.08.2016 10:59Забавный у Вас робот, если он может себе позволить остановиться на десять секунд, чтобы найти свое место. Что Я Делаю Не Так?
И по поводу квадратного сигнала — есть еще термин прямоУгольный, с ударением на у, тоже неплохо. хотя и не так любимо в электронике.
По самому тексту — способ прикольный, хотя и весьма ограниченный в своем применении, только для сигналов, принимающих 2 значения, лично мне интегралы понятнее.
haqreu
26.08.2016 11:06Я открою вам секрет, робот вполне может предполагать, где он находится. Например, по одометрии. Только с одометрией накапливается ошибка, которую можно иногда сбрасывать, остановившись на десять секунд.
А про способ, похоже, большинство тут присутствующих не очень поняли, что я не предлагаю так ничего считать. Я предлагаю только иметь ментальную картинку. Самым важным в этом тексте является именно связь между роботом и рядом Фурье, почему и как уходят разные частоты сигнала.

hardegor
26.08.2016 10:56+2Стоит добавить картинку — меандр и наложенные на него несколько синусоид с указанием вычисленных амплитуд, тогда наступит некоторое просветление, как меандр раскладывается на синусоиды или как из них получить меандр.

haqreu
26.08.2016 14:26Вот картинка, любезно присланная hardegor:


MichaelBorisov
30.08.2016 20:58+1Картинки что, от руки рисовали? Синусоида наименьшей частоты слева мало похожа на синусоиду. Далее, правый нижний график справа — колебания суммы должны иметь разную амплитуду, увеличивающуюся ближе к краям импульсов (явление Гиббса), а здесь они равновеликие.
К слову сказать, такое приближение прямоугольника суммой синусоид, чтобы колебания были равновеликими — это весьма трудная задача на минимакс-приближение. Решается только итерационными методами. Встречается в задачах расчета цифровых фильтров.
rafuck
30.08.2016 22:55По поводу синусоиды, не похожей на синусоиду, на мой взгляд придирка. А вот про всплески у границ ступенек, осмелюсь привести ссылку на график в вольфраме (там их очень хорошо видно):
http://www.wolframalpha.com/input/?i=sin(x)%2Bsin(3x)%2F3%2Bsin(5x)%2F5%2Bsin(7x)%2F7
MichaelBorisov
30.08.2016 23:19По поводу синусоиды, не похожей на синусоиду, на мой взгляд придирка.
Ну реально непохожа. Может быть, у вас глаз не такой наметанный, а я синусоиды ем на завтрак. Попробуйте начертить реальную синусоиду того же периода поверх приведенного графика и сравнить. «Синусоида» из рисунка — это скорее отрезки прямых, соединенные дугами окружности.
А вот про всплески у границ ступенек, осмелюсь привести ссылку на график в вольфраме (там их очень хорошо видно)
Ну да, я про это и говорю. Должны быть всплески, а на рисунке их нет.
rafuck
30.08.2016 23:24Кстати, там нигде и не написано, что это именно синусоиды :) Надо бы узнать, что за функция обозначена через s_i(t). Может на них действительно все хорошо получается.

rafuck
30.08.2016 23:32Посмотрите даже на сумму s_0(t)+s_1(t). Там «синусоида» выходит за границы импульсов сверху и снизу, и это, мне кажется, не ошибка. Просто мы чего-то не знаем :) Надо смотреть первоисточник, из которого взята картинка.

kernelmode
26.08.2016 11:44+2Вот еще очень хороший материал, дающий интуитивные объяснения по теме
https://betterexplained.com/articles/an-interactive-guide-to-the-fourier-transform/

vadbond
26.08.2016 12:05У вас есть два вектора вещественных чисел со 44100 элементами, соответственно можно посчитать одно скалярное произведение. Что значит сдвиг вектора вправо и как получаются 44100 скалярных произведений?

haqreu
26.08.2016 12:08Операция циклического сдвига вектора: есть вектор [a,b,c]. Один раз сдвигаю вправо, получаю вектор [c,a,b].
Если мы сдвинем вправо трижды, снова попадём на [a,b,c]. Мне интересно, какой именно из сдвинутых векторов имеет наибольшую корреляцию (суть есть скалярное произведение с точностью до нормализации данных). Вектор из 44100 компонент можно сдвинуть 44100 раз до момента получения исходного.

dcc0
26.08.2016 13:36«Лично я неспособен к синтаксическому подходу, я в цепи из двух формул обязательно потеряю какой-нибудь минус».
Оооот, истину возвещает автор. Всегда не понимал, как с этими значками быть и от математики хотелось бежать. Увы! Математика на яблоках меня тоже не всегда удовлетворяла, так как в школе считал, что яблоки надо есть = )
Для себя по поводу формул сделал вывод — мне проще понять, когда я знаю, что есть в начале и что нажуно получить, сколько шагов до результата…

sena
27.08.2016 09:18> Пики щелчков приходятся в каждом из 3600 кусков на одно и то же место, а остальной шум размазан более-менее равномерно по всей длине, в итоге шум уходит.
А что если частота щелчков немного плавает и пиков не получится?
haqreu
27.08.2016 09:19А вот тут будет горько и обидно. Впрочем, если вы конкретно про робота, то, конечно же, ему хватит десятка секунд. Даже с плавающей частотй будет сносно.

sena
27.08.2016 14:14А есть готовые алгоритмы, которые позволят фильтровать щелчки с сильно плавающей непредсказуемой частотой?

haqreu
27.08.2016 14:41Рецепта на все случаи жизни точно не существует. Всё сильно зависит от реальных характеристик.

MichaelBorisov
30.08.2016 21:02Есть алгоритмы, которые позволят фильтровать щелчки, появляющиеся псевдослучайным образом. Еще лучше (с точки зрения громкости звука, используемого для навигации) использовать не щелчки (импульсы по сути), а псевдослучайный белый шум. Основа для подобных методов — последовательности, генерируемые сдвиговым регистром с обратной связью (LFSR). Методы применяются в современной радио- и эхолокации. Засечь радар, который излучает не мощные импульсы, а слабенький широкополосный шум, сложнее из-за того, что энергия шума размазана как во времени, так и в частотной области.

2mugik
27.08.2016 09:18Спасибо за статью.
«Координаты красной точки (центра тяжести графика) и есть нужные нам интегралы (с точностью до умножения на константу, ну да это не суть). Кстати, а можете сказать, почему именно так?»
Что-то не смог( Хотелось бы понять.
haqreu
27.08.2016 09:23Интеграл — это площадь подграфика функци. Если грубо, то это среднее значение сигнала умножить на время интегрирования. Центр тяжести — это именно среднее значение сигнала, причём по оси абсцисс и ординат они независимы (сепарабельны). Сигнал по оси абсцисс f*cos, сигнал по оси ординат f*sin. Итого падаем ровно на определение Фурье.
Скрытый текстПравда, с переходом к полярным координатам и центром тяжести есть один небольшой нюанс, но для нашей конкретно функции роли не играет.
stavenko
31.08.2016 09:50Скажите пожалуйста, интеграл — это площадь, то есть это число, одно.
А вы говорите о центре тяжести — это два числа.
Мы получается сначала сложили все столбики параллельные y, а потом сложили столбики параллельные х?
haqreu
31.08.2016 10:53-1Так нам и надо два интеграла, один для коэффициента an, другой для коэффициента bn. Игрек координата центра тяжести — это интеграл с синусом, икс координата — это интеграл с косинусом.

2mugik
27.08.2016 10:27+1Но почему именно 2/pi от центра? Т. е. численно понятно что определенный интеграл sin от 0 до pi/2 =1. Это площадь. Делим на длину pi/2 и получаем среднее значение 2/pi. Но как это представить графически? Например есть ось y — половина у нее 1/2. Теперь транслируем на ось y четвертушку круга и… бац среднее уже больше, а именно 2/pi. Это понятно что верхний конец дуги четвертушки транслируется плотнее нижний. Но почему именно такое соотношение средних? Как то бы эту дугу четвертушки даже не знаю как-то развернуть штоли чтобы понять закономерность «плотностей» трансляции. именно числом каким-то.

haqreu
27.08.2016 11:12-1Вы хотите понять, как это можно в уме посчитать, но при этом не интегрировать синус напрямую? Вариантов много, давайте я вам приведу два:
первый, обратите внимание, что автор цитирует ровно тот самый доклад Пуанкаре, о котором я говорил!
второй
2mugik
27.08.2016 13:51да, Спасибо. про первый можно как-то ссылку поправить чтобы картинка (fig 7) вошла?

haqreu
27.08.2016 14:39Картинка тут.
На всякий случай, как такое ищется: смотрите, что искомая статья напечатна в сборнике докладов Эдинбургского математического сообщества в 1905м году. Смотреть можно на scholar.google.com.
Затем идёте на сайт журнала и выбираете нужную часть. В нашем случае все картинки в конце сборника докладов.

webhamster
27.08.2016 12:21Так что же сказал Фейнман? Вы обещали объяснить суть того, как воспринимать формулы, и для этого перешли на английский язык.
Что мелочиться, можно было и всю стать на английском написать.
haqreu
27.08.2016 12:41-1Если вам непонятен английский, и при этом вы не можете найти перевод сами, то просто попросите ссылку. Не надо агрессии, от этого желание отвечать пропадает.
На самом деле я не всегда тыкал пальцем в небо: обычно под моими догадками была определенная основа. Я придумал схему, которой пользуюсь и по сей день, когда кто-то объясняет мне что-то, а я пытаюсь это понять: я придумываю примеры. Скажем, в комнату входят математики в чрезвычайно возбужденном состоянии с потрясающей теоремой. Пока они рассказывают мне условия этой теоремы, я в уме строю нечто, что подходит ко всем ее условиям. Это легко: у вас есть множество (один мяч), два непересекающихся множества (два мяча). Затем, по мере роста количества условий, мои мячики приобретают цвет, у них отрастают волосы или что-нибудь еще. Наконец, математики выдают какую-то дурацкую теорему о мяче, которая совсем не подходит к моему волосатому зеленому мячику. Тогда я говорю: «Ложь!»
— Ричард Ф.Фейнман. «Вы, конечно, шутите, мистер Фейнман!»

agarus
28.08.2016 11:40"… между нашим сигналом (квадратной волной) и функциями cos(nx), sin(nx) мы ищем скалярные произведения. То есть, мы смотрим, насколько наш сигнал похож на cos(nx) и насколько он похож на sin(nx)."
Вот очень странное утверждение. Одно дело однотипные вектора с яркими выбросами перемножать и искать наибольшее произведение. А другое дело перемножать одинаково периодичные функции сдвинутые по фазе и потом еще и множить их на нашу случайную ф от х. Что же мы тогда под «похожестью» понимаем…
haqreu
28.08.2016 12:46Подождите, при чём тут яркие выбросы? Вектор (1,1) и (1.2,0.8) имеют яркие выбросы? К кому (1,1) ближе, к (1.2,0.8) или к (-1,1)? Скалярное произведение нам собственно скажет, что к первому. Функции (патологические не берём, ладно?) от этого вектора не отличаются вообще ничем.

agarus
28.08.2016 16:43Яркие выбросы просто удобные ориентиры, для образного восприятия. Мы множим две функции Ф и синус и интегрируем их. Это как-то мне совсем не представляется мерой сходства. Грубо говоря ваш виток из проволки превращается в хитро изогнутую проволоку. Потому что в том месте где у вас стоит f:
x = r cos(alpha),
y = r sin(alpha).
А что у нас стоит под знаком интеграла в формуле для a1 и b1? Правильно, f sin(t) и f cos(t).
Должно стоять f(t) и ровного витка там не получится. f также зависит от (t) как и синус с косинусом, верно?
пс.пардон промазал.
haqreu
28.08.2016 18:19Подождите, я перестал понимать.
Давайте возьмём f=sin(x+.001). На кого эта функция больше похожа, на sin x или на cos x?
В первом случае скалярное произведение integrate ( sin(x+.001)* sin(x))dx даст почти единицу, во втором случае почти ноль.
Следовательно, наша искомая f скорее похожа на синус, нежели на косинус.
Если же мы захотим нарисовать это дело, как я сделал, то надо «намотать» sin(x+.001) вокруг начала координат. Вы получите «лепесток» (на самом деле двойной, ну да не суть), смотрящий наверх. Он будет почти симметричным относительно оси ординат, таким образом, центр тяжести будет почти лежать на оси ординат, говоря о том, что на косиус (ось абсцисс) наша функция непохожа.

stavenko
31.08.2016 09:55+1Спасибо добрый человек. Вот эта вот аналогия со скалярным произведением — это просто отличая идея.
Пойду попробую теперь объяснить своей девушке.






kluwert
Т.е. вы хотите сказать, что после прочтения вашего весьма сбивчивого опуса читатель вдруг вскрикнет «Эврика!» и тут же переоткроет теорему Винера-Хинчина? Кстати, перед тем как использовать понятие «скалярное произведение», которое обычный среднестатистический технарь помнит только по векторам из курса школьной математики, нужно, наверное, сказать несколько слов о пространстве L2, об обобщении понятия «скалярное произведение» на это пр-во. Да и, кстати, уж коли речь идёт о ПФ от даже не непрерывного сигнала, какие-то словеса нужно сказать об обобщённых функциях, не? А то ведь вдумчивый читатель может начать задавать вопросы о правомерности интегрирования бесконечной последовательности прямоугольников и т.д.
haqreu
Нет, не хочу. Я даю пищу для размышления, каждый пусть делает с ней, что хочет. Почитайте статью Пуанкаре всё же для начала и не ищите проблемы там, где её нет. Пожелание одной фразой описать все патологические случаи похвально, но именно этим в итоге и пугает людей, при всём том, что математика — это просто.
Пространство L2 — это прекрасно, но для иллюстрации напрочь не нужны лебеговы меры, бесконечноразмерные пространства и тому подобное. И обобщённые функции тоже ни к чему там, где можно обойтись обычной. Да не просто обычной, а я вам хуже скажу, сэмплированием обычной.