Постановка задачи
На днях я увидел на просторах интернета крайне любопытную вещь: мендосинский двигатель. Ротор на подшипниках крайне низкого трения: оригинальный имел стеклянный цилиндр, подвешенный на двух иголках, современные имеют магнитный подвес оси. Двигатель бесколлекторный, на роторе подвешены солнечные батареи, которые выдают напряжение на катушки, намотанные на роторе. Ротор проворачивается в фиксированном магнитном поле статора, солнечная батарея уходит от направленного света, на её место приходит другая. Крайне элегантное решение, которое вполне под силу сделать дома каждому.
Вот на этом видео крайне подробно описан (на русском языке) принцип работы:
Но ещё больше самого двигателя мне показалась любопытной следующая вещь. В описании этого видео Дмитрий Коржевский написал следующую вещь: «Боковую опору заменить магнитом НЕВОЗМОЖНО!!! Не задавайте больше этот вопрос!»
Отмазка: я ни разу не физик, могу сильно ошибаться, поправки приветствуются.

О, это интересно. Давайте ещё раз посмотрим, как работает магнитный подвес ротора. Если мы поставим два магнита, то изолиния потенциала выглядит следующим образом в зависимости от расстояния между двумя магнитами:
То есть, мы ставим два фиксированных магнита на статоре. Магнит на оси ротора не захочет сдвинуться вбок, т.к. изолиния потенциала имеет некий локальный минимум. Он захочет выскочить вдоль оси ротора. Делаем две таких системы, получаем ось ротора, которая зафиксирована магнитным полем в радиальном направлении, но при этом нестабильна в продольном. Упираем ось в стеклянную стеночку и вуаля, получили подшипник слабого трения.
Но стеклянная стеночка — это как-то… неэлегантно, что ли? Вполне логично желание получить полностью парящий в воздухе ротор, безо всяких костылей. И явно Дмитрия затюкали этим вопросом, да так, что он был вынужден написать невозможность подобного прямо в описании видео. И ведь Дмитрий Коржевский не один такой.
Давайте посмотрим сюда, цитирую:
What would happen if the base magnets were spaced and oriented like in this drawing? Would it give it stability in the axial plane, and do away with the mirror requirement?
Или сюда, цитирую:
On a Mendocino Motor why does one side float free while the other has a tip to a wall? I know the question might sound trivial but I have worked up the idea why not use the same magnets used to levitate as a counter force on both sides of the shaft? I attached a very rough jpg of what I mean. the green magnets at the end of the shafts is what im referring to. is there some theory or law preventing this?
То есть, люди по всему миру хотят избавиться от механической поддержки оси. Я в школе учился плохо и мне невозможность создания полностью магнитного подвеса без костылей тоже ни разу не очевидна. При случае я за чашкой чая задал своему начальнику, учёному с мировым именем (не физику, прикладному математику), этот вопрос: «А почему, собственно невозможно?» И знаете, ему это тоже не было очевидно!
На вышеозначенных форумах никто толком не объяснил, почему это невозможно. В лучшем случае цитировали какую-то теорему Ирншоу, которая не слишком-то удобоварима. Итак, она гласит следующее: «Всякая равновесная конфигурация точечных зарядов неустойчива, если на них кроме кулоновских сил притяжения и отталкивания ничто не действует.» Вам ясно? Мне нет. Положим, я могу смириться с тем, что мы говорим про заряженные частицы, а не про магниты. Но дальше?
Первая иллюстрация
Когда мне что-то неясно, я рисую картинку. Для простоты она будет в двумерном пространстве. Давайте представим четыре закреплённых единичных заряда по углам квадрата и свободный заряд в центре квадрата. Примерно так:

Неужели свободный заряд не находится в состоянии устойчивого равновесиия? Ведь куда бы он ни двинулся, он приближается к одному из фиксированных зарядов, увеличивая силу отталкивания! Давайте попробуем нарисовать карту потенциальной энергии свободного заряда. Я в школе учился плохо, физику прогуливал, поэтому будем черпать знания из википедии. Итак, если мы имеем в пространстве только один закреплённый заряд, то он создаёт во всём пространстве электростатический потенциал.
Формула электростатического потенциала (кулоновского потенциала) точечного заряда в вакууме:
Во всех умозрительных опытах все коэффициенты у меня равны либо нулю, либо единице. Поэтому заряд q единичный, неясный k тоже единица. То есть, один закреплённый заряд создаёт потенциал, измеряемый по формуле 1/r, где r — это расстояние до заряда.
Потенциальная энергия свободного единичного заряда в поле нашего закреплённого заряда также равна 1/r. (Вообще говоря, энергия равна k*q1*q2/r, но коэффициенты выбираем так, чтобы было удобно считать). Для нескольких зарядов все потенциалы просто складываются.
Давайте рисовать карту потенциальной энергии нашего свободного заряда, я это делаю при помощи sage:
var('x,y')
def unit_potential(a,b,x,y): return 1/(sqrt((x-a)^2 + (y-b)^2))
def system_potential(x,y): return unit_potential(1,1,x,y)+unit_potential(-1,1,x,y)+unit_potential(1,-1,x,y)+unit_potential(-1,-1,x,y)
contour_plot(system_potential(x,y), (x, -2, 2), (y, -2, 2), cmap='hsv', contours=30, region=5-system_potential(x,y), figsize=12, colorbar=True)
Вот карта, я выколол точки, где потенциальная энергия уходит в бесконечность:
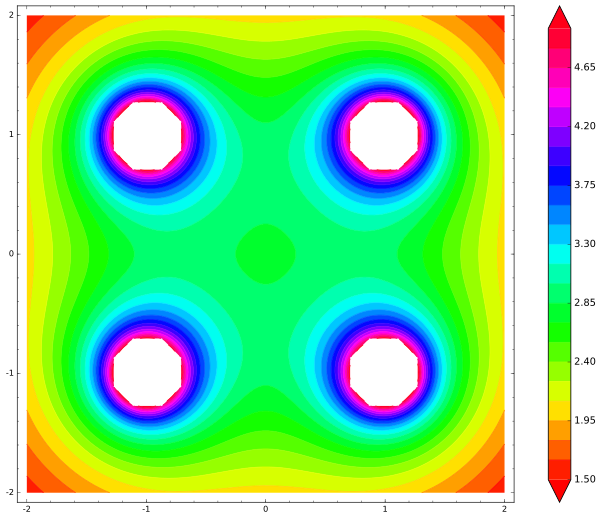
По центру квадрата чётко виден локальный минимум энергии. Куда бы ни двинулась частица из центра, энергия будет увеличиваться, поэтому от небольших возмущений она явно захочет вернуться назад в центр, это точка устойчивого равновесия. Неужели Ирншоу соврал? Нет, он не соврал. Проблема в том, что я плохо нарисовал картинку. И многие ошибаются ровно так же, как и я. Остановитесь сейчас, подумайте, где я ошибся?
В данном случае ошибка в том, что в двумерном пространстве закреплённый заряд создаёт потенциал, измеряемый по формуле -ln r, где r — это расстояние до заряда, а вовсе не 1/r. Давайте на некоторое время вы мне поверите на слово и разрешите неясным образом изменить кулоновскую формулу, тогда корректный код будет выглядеть вот так:
var('x,y')
def unit_potential(a,b,x,y): return -ln(sqrt((x-a)^2 + (y-b)^2))
def system_potential(x,y): return unit_potential(1,1,x,y)+unit_potential(-1,1,x,y)+unit_potential(1,-1,x,y)+unit_potential(-1,-1,x,y)
contour_plot(system_potential(x,y), (x, -2, 2), (y, -2, 2), cmap='hsv', contours=30, region=5-system_potential(x,y), figsize=12, colorbar=True)
Вот картинка с картой потенциальной энергии:
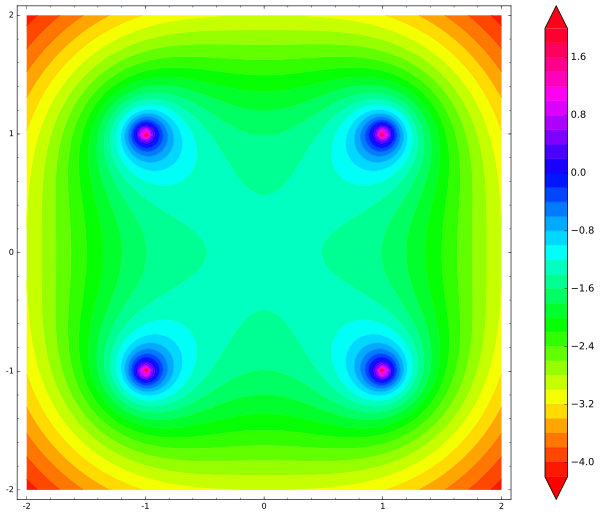
Обратите внимание, что локальных минимумов на карте нет. Центр квадрата — седловая точка, то есть, точка неустойчивого равновесия. Как только свободный заряд сдвинется хоть на микрон от центра квадрата, он обязательно скатится и вылетит из квадрата, ускоряясь и ускоряясь.
Секунду, что всё же произошло с формулой потенциала?
Когда я получил явное противоречие с теоремой Ирншоу, я понял, что где-то прокололся и стал искать ошибку. Ошибку искать лучше всего последовательно с самого начала. Я тяжко вздохнул и пошёл читать, что такое уравнения Максвелла. В школе я учился не то, что бы очень плохо, оценки у меня были отличными. Только знаний вынес явно не по всем предметам. Например, уравнения Максвелла мне разве что в кошмарах снились после школы, а в университете и далее с ними сталкиваться просто не приходилось.
А оказалось, что там всё крайне просто, особенно если мы интересуемся только электростатикой! Уравнений Максвелла четыре по количеству следующих законов:
1. Закон Гаусса, он нам пригодится. Пока оставим всякие дивергенции, «на пальцах» это просто закон сохранения: энергия из ниоткуда не берётся и в никуда не уходит.
2. Закон Гаусса для магнитного поля — те же яйца, вид сбоку. Да и магнитным полем я пока не интересуюсь, т.к. разговор идёт от заряженных частицах, пропускаем.
3. Закон Фарадея: если мы двигаем магнитами, то они порождают электрическое поле, это интересно, подробнее поглядим потом.
4. Закон Ампера: если мы двигаем электрическим полем, то порождаем магнитное. На фиг, неинтересно.
Итак, эти четыре закона связывают между собой два векторных поля E и B, электрическое поле и магнитное. Эти векторные поля — это функции, которые имеют четыре аргумента (x,y,z,t), и каждой четвёрке аргументов сопоставляют один трёхмерный вектор. Магнитное нам не очень интересно в данном случае, рассмотрим поле E(x,y,z,t). Причём не забываем, что мы интересуемся электростатикой, поэтому E постоянно во времени. Очень удобно рассматривать это векторное поле как некоторую реку, где каждой в каждой точке реки мы говорим, куда и с какой скоростью течёт вода.
Закон Фарадея говорит о том, что в случае постоянное во времени поле E (мы же говорим про электростатику) не имеет вихрей.
Как связан электростатический потенциал с электрическим полем? Очень просто: если поле E безвихревое (наш случай), то возможно создать такой ландшафт u, что покрыв его метровым слоем воды (на всех высотах!) и «отпустив» эту воду, скорость и направление течения воды породит поле E. Если умными словами, то можно найти такую скалярную функцию u, что её градиент равен полю E.
Закон Гаусса говорит следующее: возьмём маленькую область пространства. Если мы в неё не поместили заряда специально, то количество
«воды», которое затекает в эту область, равно количеству, которое вытекает. Если хочется выпендриться, то можно сказать, что дивергенция поля E равна нулю.
Напоминаю, что поле E — это производная скалярной функции u. Если её дивергенция равна нулю, то это означает, что лапласиан функции u равен нулю. Лапласиан — это умное слово для обозначения «кривизны» функции. В случае функции одной переменной лапласиан — это просто вторая производная. Вторая производная равна нулю только у постоянной или линейной функции (логично, кривизна равна нулю). В случае функции двух переменных лапласиан — это сумма двух частных производных. Если он равен нулю, то кривизна в одном направлении обязана быть аннулирована кривизной в другом направлении. То есть, чипсы разрешены:

А вот локальных минимумов (максимумов тоже) функция с нулевым лапласианом не имеет. То есть, чипсы разрешены, а холмы нет:

Представьте, что мы обмакнём проволочное колечко (хорошо изогнутое) в мыльную воду. Тогда мыльная плёнка образует поверхность с нулевым лапласианом:

Это будет так называемая минимальная поверхность. Мыльная плёнка старается уменьшить свою площадь. Логично, что если бы на ней был некий локальный максимум, то сгладив его, мы получили бы плёнку меньшей площади. Поэтому их и нет. Итак, электростатический потенциал — это своего рода минимальная поверхность, локальных максимумов (в местах, куда мы специально заряд не помещали) не имеет.
Функция 1/r имеет нулевой лапласиан в трёхмерном пространстве, а вот в двумерном нет! Если мы хотим рисовать двумерные примеры, то нам нужно решить задачу Дирихле, я о ней уже говорил в одной из своих предыдущих статей. Для 2D это будет функция -ln r.
Update: хороший комментарий chersanya, проясняющий суть магии.
Теорема Ирншоу и её следствия
Итак, возвращаясь к нашему примеру с одной свободной заряженной частицей. Потенциал электростатического поля не имеет локальных минимумов, и, как следствие, потенциальная энергия одной частицы локальных минимумов не имеет. Поэтому одна частица не может находиться в состоянии устойчивого равновесия в постоянном поле. Поздравляю вас, мы только что доказали теорему Ирншоу. Но вот как быть с более сложными системами? Как применить эту теорему к ним?
Вот очередной пример, предложенный моим начальником, который должен был опровергнуть теорему Ирншоу. Давайте зафиксируем два заряда и создадим подвижное тело, состоящее из невесомой нерастяжимой палки с зарядами на обоих концах:

Интуитивно, если мы слегка сдвинем палку влево (вправо), то один из концов приблизится к фиксированным зарядам, и они его оттолкнут, вернув палку в изначальное положение. Где же подвох? Давайте нарисуем электрстатический потенциал двух фиксированных зарядов:
var('x,y')
def unit_potential(a,b,x,y): return -ln(sqrt((x-a)^2 + (y-b)^2))
def system_potential(x,y): return unit_potential(0,1,x,y)+unit_potential(0,-1,x,y)
contour_plot(system_potential(x,y), (x, -2, 2), (y, -2, 2), cmap='hsv', contours=30, figsize=12, colorbar=True)
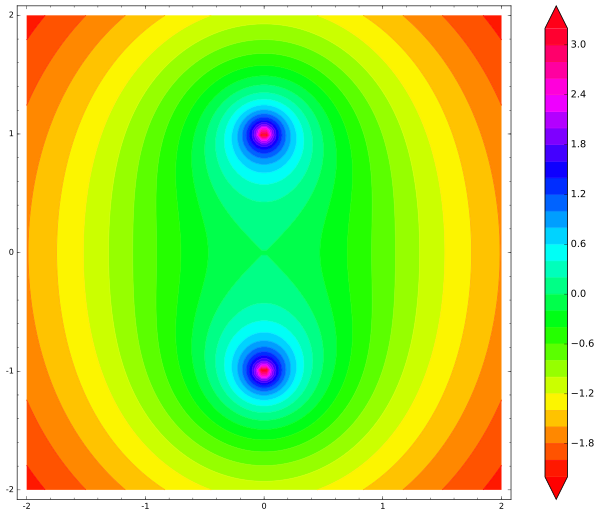
Как нарисовать потенциальную энергию нашей заряженной по концам палки? Палка имеет три степени свободы (две на перемещение и одна на вращение), поэтому график будет четырёхмерным. Давайте попробуем проигнорировать вращение и разрешим палке только параллельно перемещаться. Зафиксируем точку на палке, например, её центр, будем рисовать карту потенциальной энергии палки для положения её центра. Тогда общая потенциальная энергия палки — это сумма потенциальных энергий зарядов на конце:
var('x,y')
def unit_potential(a,b,x,y): return -ln(sqrt((x-a)^2 + (y-b)^2))
def system_potential(x,y): return unit_potential(0,1,x,y)+unit_potential(0,-1,x,y)
def energy(x,y): return system_potential(x+2,y)+system_potential(x-2,y)
contour_plot(energy(x,y), (x, -3, 3), (y, -2, 2), cmap='hsv', contours=30, figsize=12, colorbar=True)
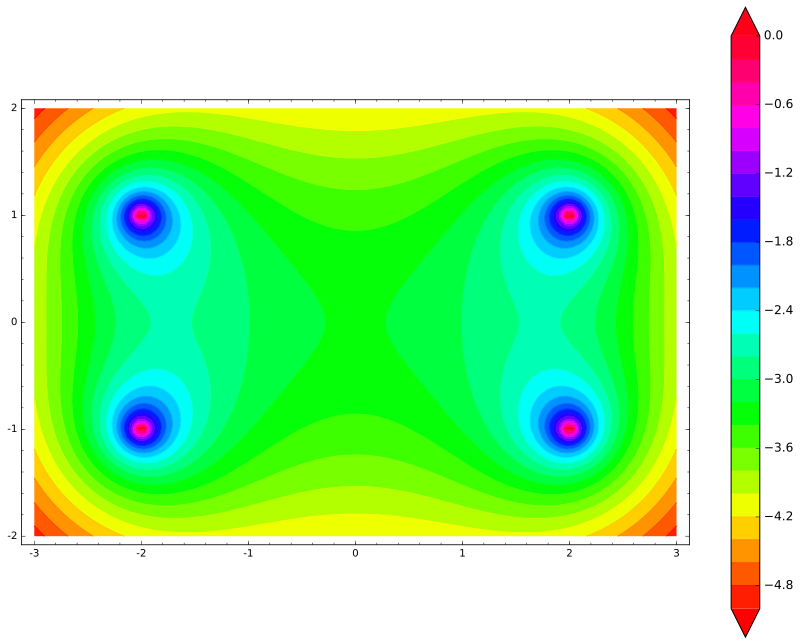
Итак, энергия палки имеет четыре пика (каждый из двух концов палки попадает на каждый из двух зарядов). Как и предполагалось, палка не захочет двигаться по горизонтали. Она убежит по вертикали!
Это логично, ведь из чего мы получили энергию? Мы сложили потенциальные энергии каждого заряда. Мы знаем, что потенциальная энергия каждого заряда — это функция с нулевым лапласианом. Их сумма тоже будет иметь нулевой лапласиан. То есть, потенциальная энергия любого (не только нашей палки!) заряженного тела не может иметь минимумов в постоянном электрическом поле!
Выводы
Ментальное изображение магнитных и электрических полей у людей, плотно не работавших с физикой, обманчиво. Мозг нас обманывает, рисуя картины минимумов энергии. К сожалению, это не так, и действительно создать мендосинский двигатель без опоры представляется затруднительным.
Какие могут быть лазейки? Теорема Ирншоу (если мы сделаем усилие и вообще применим её к магнитам) применима только системам неподвижных постоянных магнитов.
1. Мы можем попытаться создать динамическое магнитное поле
2. Диамагнетизм и всякие сверхпроводники также не входят в рамки теоремы Ирншоу
3. Подвижные вообще и вращающиеся в частности тела также не рассмотрены, наиболее известный пример левитрон
Так что, не всё ещё потеряно. Да, использование любой из этих вещей убьёт начисто лаконичность мендосинского двигателя, но магия свободно парящих в воздухе вещей перекроет всё!
Update:
Именно теорема Ирншоу показала невозможность существования твёрдой материи, таким образом отвергнув существовавшую модель строения атома. В итоге была построена планетарная модель атома.
Комментарии (216)

lnroma
27.03.2016 01:21-3А если добавид по магниту чуть в перед и назад. Таки образом чтобы сила 'пререднего' и 'заднего' магнита действовали на магинты оси, отталкивая их на встречу друг друга. Надеюсь вы меня поняли.

Zlobober
27.03.2016 02:08+11Очень хорошее изложение! Как человек с математическим образованием, не нашедший достаточно времени в школе на физику, я получил искреннее удовольствие от прочтения.
rPman
27.03.2016 02:28+2У меня только один вопрос, возникающий собственно из утверждения, что локального минимума у поля с несколькими постоянными магнитами нет и причина в том что магнитные поля складываются, взаимодействуя друг с другом (я надеюсь точно понял текст в статье?).
А если его создать 'правильное сложение' искусственно, сделать так чтобы магниты не воздействовали друг с другом, т.е. разместить их подальше, а воздействие передавать креплением из диамагнетика.
Наидубовейший пример:
- два магнита повернутые одним полюсом друг к другу, будучи не закрепленными будут стремиться:
a) оттолкнуться
b) развернуться, причем у нас две степени свободы
c) сдвинуться (так же две степени свободы) - чтобы уравновесить a) мы закрепляем два магнита на концах стержня (достаточно длинном, чтобы нивелировать воздействие магнитов на его концах, плюс еще столько же), полюсами вдоль, и закрепляем вторую пару магнитов напротив них,
- таким образом любое движение вдоль стержня будет остановлено
- чтобы уравновесить сдвиг в сторону, мы создаем еще два точно таких же стержня, размещая их под углом 90 градусов к первому и друг другу, жестко соединив их за центры.
- таким образом мы ограничиваем сдвиг, так как любое движение будет уменьшать расстояние между какой-либо парой магнитов
- чтобы уравновесить поворот, мы размещаем на каждом стержне по два магнита, полюсами перпендикулярно стержню но на расстоянии 1/4 от концов, и фиксируем для каждого парный магнит, повернутый к нему тем же полюсом. Магниты на каждом стержне размещаем в одной плоскости, но направленные в противоположные стороны,
- таким образом поворот вокруг каждой оси (стержня) будет блокироваться магнитами на соседних стержнях.
- таким образом поворот вокруг каждой оси (стержня) будет блокироваться магнитами на соседних стержнях.
Я ничего не упустил?
Заголовок спойлера

Fullmoon
27.03.2016 09:01Ничего не понял.
Да, запрет Ирншоу в магнитостатике обходится введением диамагнетиков, но вы тут используете их просто как жёсткие связи. Если отвлечься от диамагнетизма, на картинке я вижу возможный поворот вокруг оси x от z к y (принимая классическую раскраску осей). Две пары перпендикулярных магнитов на z ничем не скомпенсированы. Аналогично обстоит дело и с другими осями.
Или вы хотите уравновесить систему за счёт участков стержней вблизи перпендикулярных магнитов? Тогда полюса надо было направить в противоположную сторону, диамагнетики из поля выталкиваются.

haqreu
27.03.2016 09:30+1А если его создать 'правильное сложение' искусственно, сделать так чтобы магниты не воздействовали друг с другом, т.е. разместить их подальше, а воздействие передавать креплением из диамагнетика.
Не получится. Во-первых, я сильно подозреваю, что вы использовали слово диамагнетик как "немагнитный материал", по крайней мере, ваша картинка на это намекает. Если нет, то я не понял. К тому же, Ирншоу ничего не говорил о диамагнетиках, левитация лягушки:
Of flying frogs and levitrons

Во-вторых, просто размещать магниты подальше, чтобы они не взаимодействовали не получится. Именно об этом статья, о том, что наш мозг нас обманывает и они взаимодействуют. А создать не непрерывное поле не получится.rPman
27.03.2016 18:41Да, я про немагнитный материал.
Не понял про 'мозг нас обманывает' и 'взаимодействие' — какое именно взаимодействие тут добавляется, ведь я использую только одно единственное свойство магнитов — отталкиваться
все остальные свойства в моей схема — паразитные (каждому я противопоставляю отдельную пару магнитов, работающих на отталкивание), вся идея состоит в том что ошибка слабее чем основное взаимодействие.

haqreu
27.03.2016 09:38+1Да, к слову, напишите себе маленький симулятор систем магнитов, будет проще, чем магниты клеить и тратить время на подозрения того, что у вас что-то несоосно. Там кода-то на пару сотен строчек максимум.

vsabadazh
27.03.2016 02:54+2Большое спасибо за статью! Интересно и захватывающе написано.
Что до стеклянного упора — мне в первую очередь пришла мысль о том, что ротор, создающий переменное поле, мог бы создавать лишние вибрации, которые могли бы как-то повлиять на магнитные подшипники. И чтобы эти вибрации погасить, применяют жестко закрепленную опору.
А оказалось, что всё куда сложнее...

thewizardplusplus
27.03.2016 08:36+2в двумерном пространстве закреплённый заряд создаёт потенциал, измеряемый по формуле -ln r, где r — это расстояние до заряда, а вовсе не 1/r
Досадно. Всегда нравился алгоритм поиска пути, основанный на электростатике: у препятствий и NPC отрицательный заряд, у цели — большой положительный. Восхищало, как красиво применили физику для целей игрового ИИ. А выходит, что физика тут по сути не при чём.
А за статью спасибо. Часто слышал, что магнитную левитацию нельзя создать на статических магнитах, и именно поэтому во всех левитирующих глобусах имеется электрическая схема на батарейках. Тоже воображение рисовало всякие группы из 4 магнитов в основании. Теперь понятно, почему это невозможно.
haqreu
27.03.2016 09:23Так а что мешает использовать логарифм и считать, что мы применяем физику? :)

thewizardplusplus
27.03.2016 10:27+1Мне кажется, с логарифмом будет совсем другое поведение. Собственно, вы описали это в статье — отсутствуют локальные минимумы.
С формулойq/rможно расставить отрицательные заряды вдоль границ улицы, поместить в конце положительный заряд и NPC побегут к нему (причём придерживаясь центра дороги, чего не будет, например, при использовании более популярного A*).
С логарифмом же, как я понял, тропинки из локального минимума вдоль улицы не получится, NPC просто вытолкнет за её пределы (то есть внутрь препятствий).
haqreu
27.03.2016 12:04Ненене, минимум будет у цели. Тропинка получится отлично, это будет просто долина в горах.

Минимума не может быть в свободной от заряда зоне. У вас же цель получить минимум именно в месте заряда другой полярности, так что, всё ок.

SpaceBrainEater
28.03.2016 15:58+3Ну почему же? На самом деле и то и то правильно, просто -ln r — для двухмерных пространств(миров), а 1/r — для трёхмерных.
Очень интересная штука получается: двумерный случай позволяет тебе искать наилучшие пути вокруг предметов (в одной плоскости), а трёхмерный — может застрять, если ты будешь искать обход в плоскости (можешь попасть в локальный минимум, как на рис. 6), но в трёхмерном пространстве он будет ещё предлагать обходить сверху/снизу.

DeepBlue
27.03.2016 09:01Функция с нулевым лапласианом может иметь локальный минимум, например, x^4 в нуле. (Или сумма четвёртых степеней координат для большей размерности.) Но, по-видимому, минимумы порядка больше 2 нельзя получить по каким-то другим соображениям (например, нельзя настолько точно установить магниты).

haqreu
27.03.2016 09:22+1Простите, но нет. x^4 — это не гармоническая функция. Обращение второй производной в ноль в одной точке, это, конечно, хорошо, но надо бы на всей области определения.

Dooez
27.03.2016 15:40Ноль это вроде как местоположение гипотетических зарядов, собственно это и есть исключение.

AntonSor
27.03.2016 10:28.Надо изменить направление силы гравитации. Т.е. расположить ротор вертикально. И подвесить его на вертикальных магнитных подшипниках. Тогда он будет свободно висеть в воздухе.
Vjatcheslav3345
27.03.2016 10:28А полимагниты для этого двигателя не подойдут? (https://geektimes.ru/post/273106/).

haqreu
27.03.2016 10:30Нет, (насколько я понимаю) это обычные магниты, просто намагниченные не просто север-юг. Левитацию только на этом не построить.

Uranix
27.03.2016 11:04Разве форма мыльной пленки удовлетворяет уравнению Лапласа? Она должна просто минимизировать свою площадь, что соответствует минимизации функционала
.
Уравнение поверхности получается таким:
haqreu
27.03.2016 11:16+3Не согласен. Минимальная поверхность минимизирует энергию Дирихле, что соответствует решению уравнения Лапаласа.

Uranix
27.03.2016 11:17+1А в каких координатах уравнение поверхности?

haqreu
27.03.2016 11:27+1Ээ… Не понимаю вопроса, в каких хотите, в тех и задавайте?

Uranix
27.03.2016 11:35+1Если задавать уравнение поверхности в виде z = u(x, y), то я не вижу ошибки в своих рассуждениях. Может вы поверхность параметризуете иначе, что у вас уравнение Лапласа получается. А еще бы хотелось увидеть обоснование
Минимальная поверхность минимизирует энергию Дирихле
Опять-таки, оператор набла там двумерный или трехмерный?
haqreu
27.03.2016 12:00+1Вот тут достаточно подробно расписано. Лично я здесь пользовался только картезианскими координатами. Размерность наблы зависит от размерности пространства...

Uranix
27.03.2016 12:02+1За ссылку спасибо, но там приведено ровно то уравнение, которое я написал вначале

haqreu
27.03.2016 12:07+1А, ну тогда я проворонил. Тогда минимизация вашей функции равнозначна минимизации энергии Дирихле.

Uranix
27.03.2016 12:14+1Простите за занудство, но все же нет. Функционал Дирихле — квадратичная форма, его минимизация приводит к линейному уравнению поверхности. Уравнение минимальной поверхности нелинейно. Иными словами, растяжение проволочного кольца по оси z не приводит к простому растяжению поверхности пленки. Но решения обоих уравнений, безусловно, удовлетворяют принципу максимума, и более того, при малых изгибах пленки она вполне неплохо описывается уравнением Лапласа.
GarryC
27.03.2016 11:41+4Мне все-таки кажется, что Вы не вполне правы с системой из4 по краям и 1 в середине, и в середине будет точка устойчивого равновесия.
Центральный заряд никуда не выскочит, дело в другом — он расталкивает все остальные, поэтому система зарядов в равновесии быть не может, что и утверждается теоремой.
haqreu
27.03.2016 11:59+2Нет, извините, вы не поняли текст. Вы ошибаетесь так же, как ошибался я в самом начале.
Я зафиксировал четыре заряда по углам. И свободный заряд в центре квадрата находится в неустойчивом равновесии.GarryC
27.03.2016 12:32+4По теореме Вы не можете зафиксировать четыре заряда по углам, поскольку для этого нужна внешняя сила.

haqreu
27.03.2016 12:37Если вам так проще, то уберите имя Ирншоу из статьи и считайте, что я доказал свою теорему, где я могу фиксировать заряды. Хотя это и нечестно, поэтому я всё же цитирую первоисточники.
GarryC
27.03.2016 13:45Так вот, к сожалению, Ваше доказательство неверно.
Проведем простейший вычислительный эксперимент.
Разместим по углам 4 одинаковых заряда и рассмотрим силы, действующие на пятый заряд на некотором отклонении от центра.
Для простоты картины отклоним пятый заряд вдоль одной из осей симметрии системы.
При этом на заряд в центре действуют Кулоновы силы, которые обратно пропорциональны квадрату расстояния между зарядами.
Возьмем сумму проекций этих сил на ось симметрии системы, причем все члены, не зависящие от отклонения, вынесем за скобку.
Данный расчет легко сделать в виде таблицы в Excel, получаем следующие результаты
для отклонения 0 сумма сил равна 0,
для отклонения 10% сумма сил равна -0.7 * К, где К — обобщенный коэффициент
20% -> -1,3; 30% -> -1,8; 40% -> -2; 50% -> -2; 60% -> -1,6; 70% -> -0.8; 80% -> 0,3; 90% -> 1,8; 100% -> 3,5.
Отсюда четко видно, что пока отклонение не составит 80% длины плеча системы или более, результирующая сила будет направлена в направлении, обратном смещению и система будет возвращаться в устойчивое состояние, если угловые заряды зафиксированы.
Вот если бы сила взаимодействия была обратно пропорциональна расстоянию, а не квадрату расстояния, устойчивого состояния не было бы.
Может, Вам следовало строить напряженность поля, а не потенциал?
haqreu
27.03.2016 14:06Вы ошиблись, использовав формулу 1/r в вычислении потенциала. Она не работает в 2d. См. самый первый пример из статьи.
GarryC
27.03.2016 14:26Да, если мы рассматриваем куб из зарядов (наверное, все-таки, 3d), то получающаяся сила стремится увеличить смещение, просто Ваш начальный пример как бы неявно подразумевал, что мы в плоскости зафиксированны.

haqreu
27.03.2016 14:27Ничего себе неявно подразумевал:
Для простоты она будет в двумерном пространстве.
Если вы сделаете те же выкладки в 3д с настоящим кулоновским потенциалом 1/r, то ваш заряд в центре куба держаться не будет.GarryC
27.03.2016 14:44На секундочку, как раз в двумерном пространстве, которые Вы приняли для простоты, он и держится, и я именно об этом и написал.

haqreu
27.03.2016 14:51Тогда ещё раз, вы ошибаетесь, используя формулу 1/r в 2d, она не работает (не является решением уравнений Максвелла).
GarryC
27.03.2016 15:03-1В любом (одномерном, двумерном, трехмерном) пространстве формула Кулоновских сил (в данном случае отталкивания) одна и обратно пропорциональна квадрату расстояния, взятого по данному пространству. Так вот, в случе одномерного пространства заряд устойчив во всех внутренних точках интервала, в случае двумерного — в некоторых из внутренних точек квадрата, в случае трехмерного — ни в одной точке куба.
Я не знаю насчет решения уравнений Максвела, но простая физика дает именно такой результат, по-моему, у вас все таки неверная терминология относительно 2d, Вы явно имеет в виду плоский срез пространства.chersanya
27.03.2016 15:08+4Если использовать формулу обратных квадратов в 1- или 2- мерном пространстве, то это соответствует ограничению передвижения зарядов по оставшимся осям каким-то другим способом. В таком случае очевидно, что можно сделать устойчивую конфигурацию — просто возьмите картонную трубку, поставьте вертикально и положите вниз её магнит. Тогда можно поместить туда ещё один магнит, который будет в равновесии — по горизонтали ему не даёт двигаться трубка (т.е. зафиксировали в одномерном пространстве), а по вертикали сила тяжести и отталкивания магнита уравновешены.
Теорему Ирншоу либо нужно применять с законом обратных квадратов — но в 3д, либо в пространстве любой размерности, но с соответствующим потенциалом. "Соответствующим" — т.е. таким, который получается из уравнений Максвелла.
haqreu
27.03.2016 15:19Если использовать формулу обратных квадратов в 1- или 2- мерном пространстве, то это соответствует ограничению передвижения зарядов по оставшимся осям каким-то другим способом.
Спасибо, вы хорошо сформулировали, у меня не получалось никак. Именно поэтому нужно менять формулу потенциала для двумерных примеров.

Arastas
28.03.2016 14:15+1Поправьте, я правильно Вас понял, что если я возьму пример с четырьмя зарядами по углам квадратов в трехмерном пространстве, и зажму эти заряды между двумя листами стекла, ограничив их перемещение по оси z, то положение в центре квадрата будет аттрактивно?

WinPooh73
27.03.2016 14:21-4Какие ещё заряды? Вам удалось получить магнитный монополь? Зачем тогда писать статьи на Хабре, бегом за Нобелевской премией! :))

haqreu
27.03.2016 14:23+5Если вы внимательно читали статью, то она вся целиком говорит об электростатике. И да, у меня монополи. Рассмотрение магнитного поля, а не электрического лишь загромождает выкладки, не внося ничего нового.
Ваш сарказм неуместен.
WinPooh73
27.03.2016 14:27+1ОК, прочитал про приближение магнитостатики и про магнитный заряд. Беру свой сарказм обратно :))

haqreu
27.03.2016 14:40+2Про сарказм: в этой статье пара дней моей работы. Меня удивляют комментаторы, с места в карьер выливающие едкие комментарии на мою работу, выказывая неуважение к ней. Если я написал глупость, потрудитесь просто объяснить, где я ошибся. Польза будет и мне, и тем кто потом прочитает. Просто поток ругани только озлобит всех вокруг.

WinPooh73
27.03.2016 17:04ОК, я отвечу как человек, потративший на изучение темы не пару дней, а несколько семестров в различных курсах не самого слабого физического вуза (МФТИ). На мой взгляд, Вы решаете одну задачу, а ответ пытаетесь выдать за решение другой. Электростатика в общем случае не аналогична магнитостатике. В реальности у нас нет магнитных зарядов, а есть только магнитные диполи. Соответственно, кулоновский закон (где 1/r) для них не выполняется, там следующий порядок малости. Вам следует решать электростатическую задачу для диполей.

haqreu
27.03.2016 17:07+1Правильно, и получим тот же самый итог, только с длинными выкладками. О чём я и написал.

NeoCode
27.03.2016 12:33Боковая опора — это просто опора, или там все-же есть какая-то фиксация для оси вращения?
Я бы провел эксперимент следующего рода — ось, упирающуюся в опору, удлинил бы длинным пластиковым стержнем, и на конце прикрепил бы магнит, опору отнес бы дальше и к ней прикрепил бы другой магнит, отталкивающий магнит на стержне. Теория теорией, а интересно было бы посмотреть на видео, как система себя поведет на практике...
haqreu
27.03.2016 12:38+1Просто опора. Да напишите же симулятор, это просто. Я не стал, т.к. фейл уже заранее гарантирован.

Ivnika
27.03.2016 12:38Возможно глупость скажу… но- а если представить что ось ротора может чуть изгибаться? А магниты по краям наклонены внутрь. Т.е. можно представить вместо оси гибкую стальную проволоку.
Правильно ли я понимаю что в этом случае боковые опоры не нужны?
haqreu
27.03.2016 12:39Нет, неправильно. Фиксированные связи можно заменять упругими, от этого мало что изменится.
А вообще вы пытаетесь сделать динамическое поле без использования батарейки, только механически. В принципе, можно попробовать, только из рамок теоремы Ирншоу вы выходите.
Ivnika
27.03.2016 12:46Я имел в виду это
https://drive.google.com/file/d/0B5cuMwPdi8ojaGQwVkFkR2tFdGc/view?usp=sharing
извините не получилось картинкой вставить

kamiel
27.03.2016 12:48понял что автор хочет избавиться от «костылей». есть такое на кольцевых магнитах. когда-то смотрел эту магию, но ссылку потерял :(
есть только краткий обзор energodar.net/ha-tha.php?str=energy/magnets/podshipnik или еще можно ролики посмотреть на ютубе
haqreu
27.03.2016 13:09Так по вашей же ссылке в видео видна боковая поддержка. В целом я верю, что можно создать что-то парящее, но только покуда вращается (см. левитрон). В покое ничего парить в статике не может.

kamiel
28.03.2016 11:07не могу картинки вставлять. смотрите последнюю в статье: нужно создать потенциальную яму где все будет парить. в общем случае надо рассматривать систему не одномерно, а двумерно, в 2-х плоскостях.
а видео там немного не то, вот нашел https://www.youtube.com/watch?v=81qZlTLxpxk (хотя качество ужасное, но других источников нет). Николаев сделал много магнитных подшипников разных типов. его полное видео вообще чистая магия)))
bromzh
28.03.2016 11:14+3В учёной среде принято публиковать свои работы в научных журналах. Если единственный источник какого-либо опыта или открытия — сомнительное видео — 99% что это лженаучная хрень.

kamiel
28.03.2016 11:43-1т.е. пока умный дядя с кучей дипломов, желательно зарубежом, не скажет вам что можно, вы не поверите?
в ученой среде (по крайней мере раньше было так) принято проверять все опытным путем. я собрал все модели что на видео и все работало. Николаев говорит в своем видео, кто он и где работал. думаю дураков туда не брали.
бросил я это дело только когда увидел японские турбины со скоростями 20-30 тыс оборотов на магнитных подвесах. вот тогда и пришло понимание, что мы уже безнадежно отстали в науке. и с подобным отношением, вряд ли уже когда нибудь догоним.
haqreu
28.03.2016 12:31+2т.е. пока умный дядя с кучей дипломов, желательно зарубежом, не скажет вам что можно, вы не поверите?
Именно так, с двумя поправками: а) зарубежные дипломы не обязательны и б) умный дядя должен быть очень не один
Николаев говорит в своем видео, кто он и где работал. думаю дураков туда не брали.
Он вполне мог до того трудиться на нормальном научном поприще, это совершенно не запрещает впоследствии стать научным жуликом. Публикуешься в рецензируемых научных журналах, имеешь цитаты и воспроизведения твоих результатов другими людьми — молодец. Присваиваешь себе громкие (для обывателя) титулы и пытаешься продавать нанофильтры (или что там Петрик делал) через госаппарат — жулик.

bromzh
28.03.2016 13:05Просто факт наличия эксперимента/открытия в рецензируемых научных изданиях обычно означает, что компетентные люди смогли воссоздать опыт и проверили на правильность теоретические выкладки за меня. Конечно, можно включить параноика, не верить никому, кроме себя и считать все эксперименты/теории по-умолчанию неверными до тех пор, пока лично не воссоздашь эксперимент или не проверишь теорию. Все эксперименты по квантмеху или ТО, которые проводятся на уникальном или очень сложном оборудовании тоже считать враньём, пока лично не запустишь какой-нибудь коллайдер и не обсчитаешь результаты?
А вот отсутствие работы в научных изданиях вызывает вопросы, почему же их там нет? Может сам опыт особой ценности не представляет? Или он не несёт в себе ничего нового? Если опыт уникальный, но за ним нет теории, то его обязательно примут во внимание. Сонолюминесценцию, например, пока не могут объяснить теоретически, но он на слуху. Если в теории есть пробелы, то возможно научное сообщество поможет их решить, Эндрю Уайлс тоже не с первого раза достиг цели.
thewizardplusplus
28.03.2016 13:40Хочу заметить про сонолюминесценцию. Вроде уже установили причину — свечение происходит из-за нагрева газов внутри схлопывающегося кавитационного пузырька (а они туда попадают из воды вокруг, т. к. были растворены в ней; в частности растворение в воде некоторого количества инертных газов усиливает свечение), а нагрев газов происходит из-за крайне быстрого сжатия (схлопывания) кавитационного пузырька.
Да, чтобы газы светились, нужна температура в тысячи кельвинов и именно такая температура достигается при схлопывании кавитационного пузырька. Тысячи при многопузырьковой сонолюминесценции и сотни тысяч (sic!) при однопузырьковой.
В случае однопузырьковой сонолюминесценции на последней стадии коллапса кавитационного пузырька стенки пузырька развивают скорость до 1-1,5 км/с, что в 3-4 раза превышает скорость звука в газовой смеси внутри пузырька.
Источник — Википедия. Да, там ещё указывается модель Швингера (основанная на изменении вакуумного состояния электромагнитного поля в кавитационном пузырьке), как возможное объяснение. Но вроде как теория с нагревом признана основной в настоящее время.
P. S.: Очень интересуюсь данным явлением. Поражает, как столь маленькие пузырьки могут развивать такие скорости сжатия и создавать такие температуры.
Особенно это восхищает в свете существования рака-щелкуна (synalpheus regalis), который охотится, щёлкая клещнёй и создавая этим струю кавитационных пузырьков, которые, схлопываясь, нагревают воду до 4500 C (https://www.youtube.com/watch?v=W9xK1AmCHIM). Температура поверхности Солнца, напомню, около 5000 C.
Температура Солнца по щелчкупальцевклещни… Красиво же!
bromzh
28.03.2016 14:00Ну википедия (особенно русская её часть) — довольно сомнительный источник информации. Банально: в русской пишут
Итак, если природа света тепловая, то необходимо объяснить, за счёт чего достигаются столь высокие температуры.
В настоящее время считается, что нагрев воды происходит следующим образом.
В английской же версии сразу стоит предупреждение:
The mechanism of the phenomenon of sonoluminescence is unknown. Hypotheses include: ...
Т.е. читателя сразу предупреждают: механизм неизвестен, есть только гипотезы. Зачем писать на русской так, как написано, я не понимаю...

haqreu
28.03.2016 14:48+1Вот тогда и пришло понимание, что мы уже безнадежно отстали в науке. и с подобным отношением, вряд ли уже когда нибудь догоним.
Не хороните российскую науку раньше времени. И уж тем более не из-за её отношения к шарлатанам.

VIK52
29.03.2016 22:44+2Наши центрифуги для разделения изотопов урана (2000 оборотов в секунду, 30 лет непрерывной работы) — ни фига мы не отстали

skyramp
27.03.2016 12:52Для простоты она будет в двумерном пространстве.
А такой переход из трехмерного пространства в двухмерное в этой задаче вообще корректен?
haqreu
27.03.2016 12:54+1Прочтите, пожалуйста, статью, она и об этом в частности. Да, корректен.

skyramp
27.03.2016 13:13А можно, пожалуйста, чуть более конкретно? я прочитал статью, но понять правильно что-либо достаточно сложно, особенно после перехода "а давайте перейдем от задачи удержания точки в точки в трехмерном пространстве к задаче удержания точки в двухмерном, ой, а она там не удерживается из за того, что это двухмерное а не трехмерное пространство". прочитав несколько раз текст выше и вокруг данного перехода его обоснование я не нашел или, к сожалению, не понял

haqreu
27.03.2016 13:25+6Да, вы действительно не поняли и исказили логику того, что я говорил. Попробуем ещё раз.
1) Рисовать примеры в 2д привлекательнее, нежели в 3д. При этом велик соблазн напрямую взять формулу из 3д и её использовать (см. кулоновский потенциал 1/r). Наверху в комментариях приведён пример с AI в играх, где так и сделано, таким образом, я не один такой.
2) К сожалению, такой прямой переход ошибочен: eсли принять за отправную точку, что электромагнитные поля являются решением системы уравнений Максвелла, то легко увидеть, что 1/r удовлетворяет уравнениям Максвелла в 3д, но не в 2д.
3) Решаем уравнения в 2д, получаем функцию потенциала вида -ln r.
4) Минимальные картинки можно рисовать в 2д, а не в 1д, т.к. функции нулевого лапласиана в 1д несколько вырождены для нашей физики.
5) Заряд не удерживается в 2д не потому, что это 2д, а не 3д, а потому, что потенциальная энергия не имеет локальных минимумов (нулевой лапласиан), это следствие уравнений максвелла, а не размерности пространства.
6) Таким образом, что в 2д, что в 3д статическая левитация невозможна.
skyramp
27.03.2016 13:48+16) Таким образом, что в 2д, что в 3д статическая левитация невозможна.
тут возникает вопрос, является ли кристаллическая решетка примером искомой левитации (просто при очень малых расстояниях), а если нет — то почему механизмы, обуславливающие существование кристаллических решеток, не применимы в данной задаче?
haqreu
27.03.2016 14:08+1Потому что с кристаллическими решётками мы уже уходим в квантовую физику.

dax
28.03.2016 00:18Звучит неубедительно. Принимая расстояние между атомами в кристаллической решетке 1 нм, до квантовых эффектов еще далеко.
Zenitchik
28.03.2016 12:08В кристаллической решётке атомы соединены химическими связями. Химическая связь сама по себе имеет минимум потенциальной энергии при некотором расстоянии между атомами.

WinPooh73
27.03.2016 14:03Если мы поставим два магнита, то изолиния потенциала выглядит следующим образом в зависимости от расстояния между двумя магнитами
Извините, не понял, о каком потенциале идёт речь? Насколько я помню из курса общей физики, магнитное поле непотенциально.
haqreu
27.03.2016 14:07О потенциальной энергии идёт речь.

WinPooh73
27.03.2016 14:23Вы можете показать, что эта энергия потенциальна, т.е. при движении по любой замкнутой траектории сохраняется при возвращении в исходную точку?

Dooez
27.03.2016 15:48В реальности магнитных зарядов не существует и линии напряженности замкнуты. Данная статья разбирает случай с электрическими зарядами, в статике уравнения магнитного и электрических полей похожи.

arheops
27.03.2016 15:50Потенциальность энергии магнитного поля доказывается в стандартном школьном курсе физики, и да, ее можно вывести из уравнений Максвела.

MichaelBorisov
29.03.2016 21:27+2Насколько я помню из курса общей физики, магнитное поле непотенциально.
В областях пространства, где отсутствуют электрические токи и переменное электрическое поле, ротор векторов H и B равен нулю, а такое поле является потенциальным (т.е. его можно представить в виде градиента некоторой скалярной функции — потенциала). См. также вики.
Магнитное поле, создаваемое постоянными магнитами, аналогично электрическому полю, создаваемому диполями. Единственная разница — это поле внутри магнитов. Оно формулами электростатики не описывается. Однако в задачах на взаимодействие постоянных твердых магнитов эта разница несущественна — нас в общем-то и не интересует поле внутри магнитов, а только снаружи их.

AndrewSu
27.03.2016 15:17«Всякая равновесная конфигурация точечных зарядов неустойчива, если на них кроме кулоновских сил притяжения и отталкивания ничто не действует.»
Я на Вашем месте не оставлял бы поиск удачной конфигурации. Ведь на систему действует еще и гравитация.
haqreu
27.03.2016 15:17+2Нет, спасибо, вечного двигателя я искать не буду. Гравитация ничему не поможет, всё остаётся точно тем же.

AndrewSu
27.03.2016 15:39Я имею ввиду не вечный двигатель, а конфигурацию без механических опор.

haqreu
27.03.2016 15:43+1В моей фразе «вечный двигатель» был использован в переносном смысле, в смысле поисков философского камня. Любая система, сотоящая только из неподвижных постоянных магнитов, нестабильна. Доказано в девятнадцатом веке. Искать надо в другом месте.

arheops
27.03.2016 15:51Существует конфигурация без механических опор для вращающегося вала(используется в магнитных подшипниках кулеров). К сожалению, с невращающимся(статическим) предметом — невозможно. Тоесть можно сделать такой же двигатель, который будет "парковаться" на ночь, а днем висеть.

haqreu
27.03.2016 15:53Ага, я о такой возможности и говорил. Поделитесь, пожалуйста, ссылкой подобный подвес? В принципе, старт "с толкача" для такого красивого двигателя — приемлемый компромисс.

arheops
27.03.2016 16:07+1Самый простой вариант — наклоняете ось(тут она тоже наклонена), ставите на стекло. На том конце, который на стекле вешаете маленький пропеллер с малым углом атаки. За счет экранного эффекта при правильном подборе ось будет висеть в несольких миллиметрах от опоры. При уходе от опоры уменьшается экранный эффект, соответсвено падает обратно. Размер и наклон оси надо подобрать так, чтоб не улетало в другую сторону. Полностью электромагнитный подшипник сделать без обратной связи — никак. Тоесть надо обратную связь какогото типа вводить(в этом примере — экранный эффект).

MichaelBorisov
29.03.2016 21:35Идея красивая, но пропеллер — это увеличение сопротивления вращению. Как бы не получилось даже хуже, чем с механической опорой.
А вот активная система стабилизации, регулятор — это с моей точки зрения более перспективно, хотя и сложно.
arheops
29.03.2016 21:40Пропеллер будет создавать очень малое сопротивление. Уж точно меньше, чем паралепипед из солнечных элементов. Нам ведь от пропеллера требуется не тяга, а экранный эффект. Потому угол атаки такого пропеллера можно делать в 5 градусов и менее. Простейший случай — диск из картона диаметром в 2см с прорезанными полосками отогнутыми на 1мм в сторону стекла.

Dum_spiro_spero
27.03.2016 15:32+1Мне статья понравилась. Тоже давно волновал этот вопрос. Это тот случай, когда «нет ничего практичней хорошей теории». Т.е. можно сразу отбросить попытки собрать хитрую статическую систему магнитов и думать о том, как проще и лучше сделать динамическое поле.
Будет ли практическая польза от этого? Вопрос. У меня есть игрушка — в стеклянной колбе вертушка с зачерненными с одной стороны лопастями — выставляешь на солнце — крутится. Работает э… почти вечно — от рассвета до заката. КПД должен определяется коэффициентом трения в оси, поглощающей способностью зачернения. Наверное можно вывести формулу — типа максимальная мощность такой системы объемом V в зависимости от этих коэффициентов и сравнить с КПД солнечной батареи.

Aclz
27.03.2016 15:43+2Хех, гляжу, это вечные грабли, на которые норовит наступить каждый.
Я когда-то с похожей целью рисовал поле двух обращенных друг к другу выпуклыми частями полусфер в three.js (что если в центр каждой поместить по заряду, и связать их жестко:

Как видно, в поперечном ("вертикальном") направлении устойчивости нет.
После чего я стянул одну из полусфер в сферу, в результате чего поле ожидаемо было вытеснено из сферы:


haqreu
27.03.2016 15:45Ну вы хоть практично к вопросу подошли и магнитов не покупали. Картинки — наше всё :)

arheops
27.03.2016 15:52Можно получить то же магнитиками и опилками.

Aclz
27.03.2016 16:21И да, магнитики в статике способны создать лишь вихревое поле, потенциальное нет.

MichaelBorisov
29.03.2016 21:49+1Необходимое условие потенциальности векторного поля — это чтобы его ротор был равен нулю. Такое поле может быть представлено как градиент поля скалярного — потенциала. По определению.
В случае системы постоянных магнитов у нас во всем пространстве, кроме самих магнитов, отсутствуют электрические токи и переменное электрическое поле, таким образом, ротор векторов H и B равен нулю. Поэтому магнитное поле является потенциальным везде, кроме пространства внутри магнитов. Так что явления, происходящие с постоянными магнитами, можно с успехом рассматривать по законам электростатики, если рассмотреть вместо магнитов соответствующие электрические диполи.
Googolplex
30.03.2016 13:36+1Стоит отметить, что необходимое условие не является достаточным — из равенства ротора нулю потенциальность может не следовать. Собственно, в следующем предложении по вашей ссылке приведён пример непотенциального поля с нулевым ротором, а именно, если поле задано на многосвязной области, то даже если оно безвихревое, оно не является потенциальным. В английской вики про это написано гораздо лучше, чем в русской.
Собственно, если мы будем рассматривать область 2D-пространства, внутри которой есть магнит, то магнитное поле в ней не будет потенциальным, потому что любой криволинейный интеграл по замкнутому пути, охватывающем этот магнит, будет отличен от нуля. В трёхмерном пространстве же "простые" сплошные магниты не являются препятствием для выполнения достаточных условий потенциальности поля (например, нет такого замкнутого пути, интеграл по которому будет будет отличен от нуля), так что действительно, магнитное поле "простых" магнитов будет потенциальным.

Aclz
30.03.2016 17:33В случае системы постоянных магнитов у нас во всем пространстве, кроме самих магнитов, отсутствуют электрические токи и переменное электрическое поле, таким образом, ротор векторов H и B равен нулю.
Магнитное поле создается орбитальными и спиновыми микротоками внутри магнита. Таким образом это поле за пределами магнита будет ненулевым вихревым (с ненулевым ротором).

MichaelBorisov
29.03.2016 21:41Красиво! Поделитесь, чем вы рисовали "опилки"? Сами писали код визуализации или библиотеку нашли?

Aclz
30.03.2016 16:54three.js (оно трехмерное, на объектах-линиях. На картинке просто отрендерен один слой).

arheops
27.03.2016 15:53+1Динамическая конструкция возможна. Не совсем понятно, почему не сделать при наличии солнечных батарей магнитный подшипник на конце. https://ru.wikipedia.org/wiki/%D0%9C%D0%B0%D0%B3%D0%BD%D0%B8%D1%82%D0%BD%D1%8B%D0%B9_%D0%BF%D0%BE%D0%B4%D1%88%D0%B8%D0%BF%D0%BD%D0%B8%D0%BA. Также можно внутрь моторчика засунуть управляющий микропроцесор и организовать отвод от стенки.

haqreu
27.03.2016 15:56Но если активные магнитные подшипники уже получили определенное распространение, то пассивные подшипники (где магнитное поле создается высокоэнергетическими постоянными магнитами, например, NdFeB) только на стадии разработки.
Чистые догадки с моей стороны: потому что солнечные батареи не выдадут достаточной мощности, а с постоянными магнитами дома не сделать? (подозреваю, что и активный дома тоже сделать затруднительно, хотя и не пробовал)
arheops
27.03.2016 16:13Не надо много энергии, надо обратная связь. Например, воздушная(экранный эффект) либо УЗ дальномер, либо оптопара(горизонтальная, нет лазера — выключаем питание дополнительного магнитика). Постоянными магнитами не сделать. Ну тут и вращение очевидно не постоянными магнитиками организовано, правда?

haqreu
27.03.2016 16:15Мощность нужна для возможности реагирования. Подозреваю, что предложенный вами вариант с экранным эффектом очень слабо отличается от просто положения неустойчивого равновесия :(

arheops
27.03.2016 16:29+1Нет, вы не правы. Давайте еще раз. четырьмя магнитами вы образуете потенциально-эквивалентную поверхность, тоесть это как сделать подкладку снизу из тефлона. Потом вы ее наклоняете например на 15 градусов относительно гравитационного поля с уклоном направо. В результате у вас болеее выгодное положении оси с магнитами на конце будет ВСЕГДА внизу справа. Собственно именно из-за этого на видео можно сделать справа поддержку(там скорее всего 1-3градуса наклона, несуть). Теперь если справа вы ось начинаете подталкивать(ну пусть пальцем), она будет подпрыгивать ровно на столько, сколько вы ей сообщили энергии(с учетом ее веса), потом возращаться на опору. Возражений нет? Вращается она всегда в одну сторону(если не всегда, можно наклонить катушки так, чтоб было всегда в одну, погрешность изготовления, ну или просто толкнуть в нужном направлении) Дальше, экранный эффект проявляется в том, что крыло(крыльчатка винта) имеет большую подьемную силу когда снизу на расстоянии порядка трети ширины крыла есть экран. Разница достигает нескольких раз. Соответсвенно можно подобрать крыльчатку так, что она не сможет на максимальных оборотах поднять всю конструкцию из гравитационной ямы, но сможет ее отодвинуть от поверхности в пределах действия экранного эффекта(на ширину самой крыльчатки). Собственно, все. Система квази-стабильна. Недостаточно оборотов — паркуется на стекло.

haqreu
27.03.2016 16:33Не очень понимаю, какое из моих утверждений неправильно. Я не оспариваю возможность динамической стабилизации. Я лишь выразил печаль в том, что работать система будет лишь в крайне узком диапазоне оборотов. И сделать на коленке практически нереально, т.к. будет требовать экстремально хорошей балансировки и т.п. И если вы повернёте двигатель на столе (посмотрите, как в видео его поворачивают), то он наверняка от малейшей вибрации застопорится. И чтобы он работал в чуть более реальных условиях, нежели один тестовый запуск в лаборатории, нужен запас по мощности.

arheops
27.03.2016 16:43+1Вы говорите, что такая конструкция не будет отличаться по усточивости. Я говорю — будет, потому, что есть обратная связь(экран). Такую конструкцию можно и без двигателя сделать(вращать ручками). Балансировка нужна хорошая, только если вы будете делать малый наклон оси и малый диаметр крыльчатки. Если вы сделаете наклон 5-10 градусов и крыльчатку из двух лопастей хотя бы миллиметров 10 с шириной на концах лопастей 7-8мм, то точность изготовления нужна малая. Крыльчатка, естественно, не должна касаться экрана. Касание например грифилем от карандаша. В видео вы можете увидеть, что мощности на вращение 10см крыльчатки — хватает. Нужная тяга — 500миллиграм. Сколько нужно — регулируется наклоном оси.

arheops
27.03.2016 16:51+1Кстати, экранный эффект ослабевает при большой скорости, потому очень вероятно, что усиление оборотов будут не так уж сильно влиять на тягу. Пробывать надо, такой эффект применяется в подшипниках гидроэлектростанций(поднимается за счет экранного эффекта в жидкости).

Dooez
27.03.2016 16:07Мне кажется проще было бы объяснить так: в любой точке потенциальтного поля есть соседняя точка, в которой энергия не больше. То есть если система выйдет из неустойчивого равновесия (что очень просто), начнется движение. На данное устройство помимо магнитных сил действуют еще и гравитационные (тоже потенциальная энергия), поэтому вверх оно двигаться не может, иначе ротор бы просто улетел.

haqreu
27.03.2016 16:13Мне кажется, что я примерно так и обяснил. Разве нет?

Dooez
27.03.2016 16:23В комментариях видимо не все поняли, я решил чуть проще написать. Таки слово лапласиан до сих пор меня пугает, и я уверен не я один такой =)

haqreu
27.03.2016 16:27Эх, видимо, картинки с чипсами и печаными дюнами не вошли :(

mixmax
29.03.2016 05:59на самом деле чипсы — это отличная иллюстрация для таких как я, кто линейную алгебру и физику уже подзабыл и не то чтобы насмерть пугается, но мучительно вспоминает все эти лапласианы) зато любит визуализации и помнит слова гиперболический параболоид, так что спасибо :)
эквипотенциальность поверхности и аналогия с чипсами в данном случае без сложных выкладок хорошо объясняет почему, как ни режь пространство на оси и не рекомбинируй заряды — в трехмерном варианте находясь в локальном минимуме в одной плоскости (предельный случай "седловина вдоль") мы обязательно попадаем в локальный максимум в другой, ортогональной ей ("седловина поперек"), что, очевидно, является неустойчивым равновесием и система из него выйдет при минимальном внешнем воздействии.

ukhanov
27.03.2016 16:45Читаем теорему внимательно: "… в отсутствие третьих сил..."
«Просто так» левитирующий магнитик ничего не нарушает?
Тогда почему система из нескольких магнитиков должна обязательно всё разрушить?
haqreu
27.03.2016 16:46Простите, но мне ваш вопрос неясен. Если вам нужен ответ, то переформулируйте, пожалуйста.

ukhanov
27.03.2016 16:52Собственно, вопрос, скорее риторический. Смысл моего коментария перекликается с замечанием https://habrahabr.ru/post/280216/?reply_to=8824294#comment_8823398 о наличии в данной системе гравитационного поля. Это означает, что нет смысла ломать копья по поводу теоремы Ирншоу — она здесь неприменима.

haqreu
27.03.2016 16:56+1Попробуйте представить себе минимум гравитационной энергии в свободном пространстве. Не получилось? Значит, Ирншоу хорошо поработал.

ukhanov
27.03.2016 17:03При чём тут это? У нас система из гравитации, магнитных сил и жёстких опор.
Моё утверждение в том, что теорема Ирншоу тут неприменима.
haqreu
27.03.2016 17:06+1Ваше утверждение ошибочно. Теорема Ирншоу применима к любым полям (и их комбинациям!) где сила взаимодействия обратно пропорциональна квадрату расстояния (я про 3д)

ukhanov
27.03.2016 17:09жесткие опоры в эту категорию не входят
chersanya
27.03.2016 17:13Опоры для заряда, который хотим левититровать — конечно не входят, иначе какая же это левитация с опорами :) А остальные заряды (которые поле создают) можно как угодно крепить друг с другом.

ukhanov
27.03.2016 17:15Правильно. Но забудьте про теорему.

haqreu
27.03.2016 17:17Неправильно, свободные заряды, что мы пытаемся заставить левитировать, можно крепить как угодно жёсткими связями между собой.

ukhanov
27.03.2016 17:21Два заряда приклееные к концам палочки находятся в состоянии равновесия — теорема не работает!

haqreu
27.03.2016 17:25Вы забыли создать внешнее поле, в котором ваша палочка должна левитировать. Можно тогда вообще сказать: система из нуля зарядов находится в равновесии.
Вы методично и безапелляционно заявляете ложные вещи и не пытаетесь слушать, что вам говорят. Я устал, дальше не отвечаю.
ukhanov
27.03.2016 22:02Я ничего не забыл. Мы говорим про теорему и её применимость, а не про левитацию. Во всяком случае я начинал с этого.

haqreu
27.03.2016 22:11Ох, вы всё упорствуете. Приведу формулировку теоремы ещё раз:
Stable levitation or suspension is impossible for a body placed in a repulsive or attractive static force field in which force and dsitance are related by an inverse square law.
Итак, теорема сформулирована. К какой именно системе она неприменима?
ukhanov
27.03.2016 22:18Ведь ясно же написано "… inverse square law." Вы вводите жесткие связи, которые этому закону не удовлетворяют. Если я выражаюсь непонятно, попробуйте почитать доказательство этой теоремы (http://studopedia.ru/3_56120_teorema-irnshou.html).

haqreu
27.03.2016 22:20Вы понимаете, что слово body в этой формулировке — это произвольное жесткое тело, которое может быть намагничено в разных местах по-разному, а не только один единичный заряд?
Та формулировка, что вы привели, существенно слабее той, что привёл я. Ирншоу доказал обе. Для электростатики я тоже в этой статье доказал обе.
ukhanov
27.03.2016 22:34-1Монополь пока не найден, поэтому магнит всегда намагничен по-разному. Но если Вы привяжете его верёвочкой, то мгновенно оказываетесь за рамками теоремы.
У меня дежавю, или я что-то упустил.
haqreu
27.03.2016 22:39+1Лично я говорил только про электростатику, возможно, вы этого не поняли. Там монополи вполне найдены. Ирншоу говорил про магнитные поля тоже, про магнитные монополя не говорил ни я, ни Ирншоу (в данном контексте, по крайней мере).

ukhanov
27.03.2016 22:48Про монополь — это просто моё занудство по поводу Вашей формулировки "… жесткое тело, которое может быть намагничено в разных местах по-разному,..." — извините.
А устойчивая система из магнитиков показана в Вашей публикации и работает исключительно благодаря опорам, в полном соответствии с теоремой, которая здесь и не работает именно из-за наличия опор.
haqreu
27.03.2016 22:55Слушайте, прекратите борьбу с ветряными мельницами и давайте попробуем разобрать всё с самого начала. Поняли ли вы всё так, как я объясняю ниже в этом комментарии?
Насколько я понимаю, вы говорите про мой последний пример, там, где четыре заряда у меня.
1) Два фиксированных заряда просто уберём, но оставим произвольное (постоянное во времени) электростатическое поле (Ирншоу говорил про любые поля с нужным законом, но я только про электростатику).
2) Итак, у меня нет ещё никаких вообще тел в моём пространстве, только от руки нарисованное поле.
3) Я туда ввожу некое свободно плавающее тело, которое состоит из палки и двух зарядов на концах этой палки. Конфигурация (длина) и заряд этой палки жёстко фиксированы, но плавать она может где угодно в пространстве.
4) Какое бы вы ни подали поле на вход, эта палка никогда не будет находиться в состоянии устойчивого равновесия.
qwertyk06
27.03.2016 23:06Вы меня таки извините, но палка по вашему это что электростатическое взаимодействие?

haqreu
27.03.2016 23:06Поясните мне, пожалуйста, электростатическое взаимодействие должно быть между чем и чем?
Я вам отвечу: оно должно быть между каждой точкой палки и окружающей средой.
Stable levitation or suspension is impossible for a body placed in a repulsive or attractive static force field in which force and dsitance are related by an inverse square law.
ukhanov
27.03.2016 23:17-1Какая сила действует между зарядами на концах палки? Если 1/r^2, то попробуйте их сблизить.
Если другая, то читаем условие теоремы и получаем ответ.
haqreu
27.03.2016 23:22Всё. Вы меня окончательно утомили. Это моя последняя попытка быть вежливым и полезным в этой ветке: два заряда на концах палки отталкиваются друг от друга, но палка им не даёт. Условие теоремы говорит о взаимодействии зарядов с окружающей средой, а не зарядов между собой. Ровно потому, что взаимодействие зарядов палки между собой может быть абсолютно каким угодно, но оно не будет изменяться в зависимости от точки пространства (см. постоянность длины палки, например). И сама палка влияет на окружающее поле, но это абсолютно не важно. До тех пор, покуда каждая отдельно точка палки взаимодействует с внешним полем по кулоновскому закону, теорема применима.

qwertyk06
27.03.2016 23:57Попробую вам ответить. Я не говорю что противоречащие закону состояния возможны. Я лишь вижу в ваших аргументах пробелы (мне так кажется на текущий момент) которые делают все ваши доказательства неактуальными.
Под body скорее всего подразумевается "заряженное тело" поскольку у вас палка не заряжена и "мешает" кулоновскому взаимодействию, то для вашей статьи она является внешней силой.
Это что касается первичной формулировки из статьи.
«Всякая равновесная конфигурация точечных зарядов неустойчива, если на них кроме кулоновских сил притяжения и отталкивания ничто не действует.»
Это вообще закон для сферического коня в вакууме!!! Взаимодействие упором это не кулоновское взаимодействие. потому что в переведённой формулировке заряды точечные!
То же что вы воспроизводите в недавних постах это совсем другой закон… И в нём я спокойно вижу другие пробелы: "in a repulsive or attractive" например… из формулировки у меня создаётся впечатление что разрешается использовать ТОЛЬКО однотипные заряды, а про внешнюю силу вы вообще ничего не привели.
haqreu
28.03.2016 00:10+2Одна формулировка является прямым следствием другой. Вот эта формулировка не предполагает никаких жёстких связей и не предполагает никаких внешних сил, только кулоновские силы между свободно плавающими зарядами:
«Всякая равновесная конфигурация точечных зарядов неустойчива, если на них кроме кулоновских сил притяжения и отталкивания ничто не действует.»
Из неё напрямую следует расширенная теорема Ирншоу, где мы уже можем создать произвольное поле, и поместить в него произвольное жёсткое тело (например, систему зарядов, связанных палочками). И единственным требованием является то, что внешнее поле создаёт кулоновские силы на тело. Ещё раз её формулировка:
«Stable levitation or suspension is impossible for a body placed in a repulsive or attractive static force field in which force and dsitance are related by an inverse square law.»
Чтобы не заниматься спекуляциями о двусмысленных трактовках языка, попробуйте понять, как она доказывается, возможно, и сама формулировка у вас прояснится. Мы не должны требовать только кулоновских взаимодействий между разными частями самого тела, жесткие связи вполне допустимы. Единственное ограничение на само тело состоит в том, что его энергия в отсутствие внешнего поля постоянна для любого положения тела в пространстве.
qwertyk06
30.03.2016 01:34В общем да, почитал я Википедию (мне хватило, дальше просто не ушёл потому что смысла не видел) там также сформулирована первичная теорема, а также кратко описываются её расширения…
Считаю последний пример автора неудачным (про заряды на палочке). Потому что доказывается теорема основная, а палочка внешняя сила… потому автор и вынужден уходить в "трёхмерность".
Там же даны и способы "обхода" данной теоремы… В частности сверхпроводники и диамагнетики…
Но про вторые я напишу ниже, под комментом с видео. (хотя если подумать требуемая для поддержки вращается и не является статической, а задача стоит удержать именно её).
PS ukhanov мне всегда казалось что диполь это 2 разноимённых заряда.
haqreu
30.03.2016 01:39Похоже, вы так и не попыталсь прочитать то, что я писал в развёрнутых комментариях на ваши вопросы. В последнем примере с палочкой я доказывал расширенную теорему Ирншоу, и палочка ну никак не является внешней силой для нашего заряженного тела, состоящего из палочки и двух зарядов.

ukhanov
28.03.2016 09:05-3Два заряда на палочке — это диполь (по определению: https://ru.wikipedia.org/wiki/%D0%AD%D0%BB%D0%B5%D0%BA%D1%82%D1%80%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B9_%D0%B4%D0%B8%D0%BF%D0%BE%D0%BB%D1%8C%D0%BD%D1%8B%D0%B9_%D0%BC%D0%BE%D0%BC%D0%B5%D0%BD%D1%82", Карл), а поле диполя отродясь не было эр-квадратом

Arastas
29.03.2016 11:12У меня такая формулировка вызывает вопросы — а что такое 'stable levitation'? Со словом stable я еще разберусь, хотя и тут могут быть разночтения, но вот слово levitation как описание положения (перемещения?) тела в пространстве мне кажется нестрогим.

haqreu
29.03.2016 13:17Stable levitation — это просто положение устойчивого равновесия под воздействием любой комбинации любых сил, подчиняющихся кулоновскому закону. Разве это нестрого?

Arastas
29.03.2016 13:511) Я не знаю, честно говоря. Возможно, что я несколько вне контекста. Но вот если бы меня спросили, как я понимаю слово levitation, я бы стал думать про гравитационное поле. Что-то вроде способности тела сохранять состояние покоя в гравитационном поле при отсутствии подвеса или опоры. Я согласен, что гравитационное поле можно заменить другим. Но всё равно, у меня в голове левитация семантически связана именно с гравитацией.
2) А вот устойчивое положение равновесия это нечётко, так как устойчивость бывает разной. Бывает аттрактивность, т.е. способность положения равновесия притягивать к себе все траектории из некоторой своей окрестности. А бывает просто устойчивость, она же устойчивость по Ляпунову, т.е., если нестрого, ограниченность траекторий системы. Рассмотрим вырожденный пример отсутствия зарядов вообще. Тогда любая точка на плоскости будет положением равновесия, все траектории ограничены и всё устойчиво, но нет ни одного аттрактора.
По контексту я думаю, что и Вы, и Ирншоу, имеете ввиду именно аттрактивность положения равновесия, асимптотическую устойчивость. Но вот если бы меня, опять же, спросили про levitation, то вряд ли я бы подумал об обязательной аттрактивности.
haqreu
29.03.2016 14:10Disclaimer: я не настоящий сварщик, я маску просто нашёл.
Слово levitation было использовано в историческом контексте именно из-за связи с гравитацией. Но сама теорема не обязательно говорит про гравитацию.
Что такое устойчивость по Ляпунову — к сожалению, я не знаю. Но пример с отсутствием поля вообще не является примером устойчивого равновесия, он является примером безразличного равновесия. Устойчивое равновесие — это точка, отклоняясь от которой, мы получаем силу, которая стремится нас вернуть в эту самую точку. Таким образом, в вашей терминологии, видимо, это именно аттрактивность.
haqreu
29.03.2016 14:15Небольшое дополнение: при отклонении от устойчивого равновесия мы не обязательно получаем вектор силы, направленный в точку устойчивого равновесия. Точка равновесия не обязана быть колодцем энергии, она может быть вортексом.

arheops
27.03.2016 16:58Без опоры один магнитик тоже не ливитирует.

ukhanov
27.03.2016 17:04
arheops
27.03.2016 17:08Ну постройте систему без опоры. Без обратной связи(явной или в виде колебания с резонансом) не получается, почему — описано в статье.

ukhanov
27.03.2016 17:12Я, возможно, не ясно выразился. Моё утверждение именно в этом и заключается. Без опор такая система не работает. Именно это и нарушает условия применимости теоремы Ирншоу.

ionicman
27.03.2016 17:03+3Спасибо за статью!
Очень было интересно почитать. Каюсь, тоже не знал про такой мотор. Сам делал только двигатель Стирлинга.
P.S. Для тех, кто не хочет возиться с балансировкой нашел дешевле: http://www.dx.com/p/neje-diy-solar-magnetic-levitation-motor-engine-transparent-black-399279

Garrett
27.03.2016 17:12+2Торт!
Спасибо за интересную статью, несмпеша почитать и подумать на досуге самое то =)

zerocool56
27.03.2016 20:12+3Есть такой персонаж на ютубе, Игорь Белецкий.
Он опытным путём, используя разные типы магнитов, пытался добиться полноценной магнитной левитации без подвесов, правда не увенчались успехом его опыты, но наблюдать их было довольно интересно.
Ссылочка на его канал www.youtube.com/playlist?list=PLeDdnFjxKZmO9NF1CWOENnCdEIPjjpXpW

AndroCAD
27.03.2016 20:23-3Тут Тимур спрашивает: "а есть видео, где этой штуке отключают свет"?
Что с ней произойдет? Хреновина зависнет, как в эксперименте "гроб Магомета" (Эффект Мейснера)? Или выскользнет в какую-то сторону? А то афтор намекает на подарочную версию, но не освещает вопрос, что будет с подарком в темноте.
haqreu
27.03.2016 20:43-1Если вы меня автором назвали, то будьте любезны не коверкать слово. И я ни на какую подарочную версию и близко не намекал.

AndroCAD
28.03.2016 18:46-1Г-дь с вами, я вас автором не называл и гостинцев от вас не ждал.
Афтор видео намекал, что это неплохой подарок и буде спрос — наклепает еще.
Ну и ответ на мой вопрос: без света, хреновина уныло висит, магниты подставки толкают стержень к боковому стеклу. Как и было сказано, особого равновесия в системе нет.

ClearAirTurbulence
27.03.2016 21:08-2Интересно, а спомощью полимагнитов, описанных тут:
geektimes.ru/post/273106
можно все-таки повесить ротор?

IT_Enot
27.03.2016 21:09-1А, извиняюсь, как насчет кокона из магнитов? Если мы мыслим в 3д пространстве, то почему магниты только в одной плоскости? Если сделать так, чтобы магниты были снизу и по бокам, грубо говоря, то можно добиться желаемого эффекта. Другой вопрос в том, как эти самые по бокам будут крепиться.

haqreu
27.03.2016 21:11+2Да, собственно, делайте кокон из чего угодно. Но локального минимума потенциальной энергии добиться не удастся. В случае электростатики зарядите, например, полую сферу. Думаете, в центре сферы будет минимум потенциала? Нет. Весь объём внутри сферы (несмотря на заряд только на поверхности!) будет иметь один и тот же потенциал.

IT_Enot
27.03.2016 21:20-1Но ведь изначальная задача была не добиться минимума в котором бы находился ротор и оставался как в блюдце, а подвесить его в воздухе как и хотели все обычные люди.

haqreu
27.03.2016 21:25+2Пассивная левитация (под действием сил, обратно пропорциональных квадрату расстояния) невозможна в любой конфигурации.

s_kozlov
27.03.2016 22:40А нельзя ли как-то использовать магнитную яму (сцепку) Николаева?

haqreu
27.03.2016 22:41Извините, не знаю, кто такой Николаев.

s_kozlov
28.03.2016 08:40некоторые ссылки и видео можно посмотреть тут
ссылка первая попавшаяся. Был еще длинный фильм по его опытам, но найти не могу.
haqreu
28.03.2016 08:53+2Слушайте, ну ведь совершенно очевидный жулик. Идём искать об этом Николаеве информацию, всего несколько кликов.
Тут говорят, что он, цитирую: «ученый-физик, исследователь аномальных явлений, автор книг по эфирной электродинамике, критик теории относительности, член-кореспондент Международной академии энергоинформационных взаимодействий.»
Звучит солидно. Идём искать, что это за академия такая. Читаем следующее: «псевдонаучное течение, претендующее на статус «науки о процессах энергоинформационного обмена в Мироздании».
Как только в России кто-то претендует на членство в академии, и эта академия не РАН, нужно моментально насторожиться. РАЕН? Жулики. Вот эта самая ЭНИО — жулики.
s_kozlov
28.03.2016 09:17Жулик или нет — пусть комиссия по лженауке разбирается, у меня компетенции не хватит так заявлять. Членство в сомнительных академиях — для меня не показатель. (Например, многие в МММ играли, но от этого не стали финансовыми спекулянтами)
Во-первых, он уже умер, не спросить. Во-вторых, эффект магнитной сцепки есть, видео полно, повторений много. Вопрос только в том, можно ли его использовать каким-то полезным способом и все.
В третьих, я ни в коем случае не призываю ВЕРИТЬ в теорию Николаева, вполне допускаю, что он ошибался в своих объяснениях, могу только повторить, что моей компетенции не хватает подтвердить или опровергнуть.
bobermaniac
28.03.2016 13:11+1Хотите я вам скину ссылку на видео с вечным двигателем?

s_kozlov
28.03.2016 13:20Я видел уже много ссылок, некоторые довольно интересны. Так что скидывайте, посмотрю с удовольствием, если что-то незнакомое. Только в личку, пожалуйста, чтоб тут не засорять.

MDiMaI666
27.03.2016 21:18-2А если где опора туда вентилятор поставить? Чтобы дула в противоположном направлении, это может послужить воздушной опорой? При изменении условий(ветер помешает) конечно оно слетит, но все же как вариант

haqreu
27.03.2016 21:19
MDiMaI666
27.03.2016 21:51То-есть все таки возможна, с экраном и обратным эффектом?

haqreu
27.03.2016 21:53Экранный эффект — это одна из разновидностей механической опоры, это не магнитная левитация.

MDiMaI666
27.03.2016 21:59Спасибо, не знал.
Можно вопрос не по теме? Кажется вы разбираетесь в этом деле.
Можно ли сделать или есть какой ни будь браслет (с датчиком холла или еще чего) чтобы отловить положения пальцев и кисти? не навешивая на сами пальцы ничего. Чтобы определить жест/ положение пальцев?
Видел какой то проект где браслет по мышцам определяет — не то.
Проект где на стол ставится устройство с размером Юсб хаба и он тоже отлавливает движения — не то.
haqreu
27.03.2016 22:01Я не специалист ни разу. Теоретически можно, замеряя электрические импульсы на коже, подобные вещи я видел в лабораторных условиях. В домашних же условиях сомневаюсь.

kemsky
27.03.2016 22:30Вопрос поставлен: можно ли убрать опору, ответ — нельзя заменить магнитом, пусть так, при этом диамагнетики не рассмотрены.
Мне кажется вопрос совсем не закрыт, можно поискать на ютубе левитацию в висмуте, например.
haqreu
27.03.2016 22:35Вы последний абзац читали? Ответ: опору убрать можно, но лаконичность и элегантность данного двигателя будет убита.

kemsky
27.03.2016 22:52Что неверно в моем комментарии?
Вы утверждаете, что будет потеряна элегантность и лаконичность, но доказательств этому в статье нет, поэтому вопрос остается открытым.

BD9
27.03.2016 22:35-2en.wikipedia.org/wiki/Electrodynamic_bearing
Здесь рассматривается открытая система, т. ч. можно достичь всего что угодно.
А так — придёте к тому, что будете рассказывать, что существование Солнечной Системы невозможно в принципе.
Ну и «картезианскими координатами» -? На русском книжек по теме не читали никогда?
haqreu
27.03.2016 22:37Эта ссылка уже была в комментариях, зачем вы её ещё раз привели?
Ну и «картезианскими координатами» -? На русском книжек по теме не читали никогда?
Не поверите, не читал. Вы чего добиться хотели? Написали бы комментарий с "декартовыми" под моим комментарием с "картезианскими" и дело с концом. Или вам охота, чтобы я начал считать ошибки в вашем сообщении? Они там есть, только я не вижу, зачем мне на них показывать.

W0lT
28.03.2016 07:55+1Отличная статья, заставила меня написать программку на скорую руку и достать из ящика магниты. Если пощупать руками, становится понятнее. Например, если вместо упора добавить отталкивающий магнит, ось с того края съедет вбок и выведет из равновесия остальные магниты. Можно еще рассказать про то, как магнитные диполи сводятся к точечным зарядам? И вот программа, если вдруг кому понадобится yadi.sk/d/NzJhMEo3qXDqp.
Скрытый текст
haqreu
28.03.2016 08:34+1Там всё довольно просто, если теорема выполняется для точечных зарядов любой полярности, то она будет выполняться для электрических диполей. Мы можем уменьшать расстояние между двумя противоположными зарядами до нуля, сохраняя дипольный момент. То есть, теорема выполняется для электрических диполей в том числе. Магнитные диполи имеют абсолютно те же самые уравнения, что и электрические (не забываем, что речь не про электродинамику!). Таким образом, она выполняется и для магнитных диполей.
Vjatcheslav3345
28.03.2016 09:33А нельзя ли изготовить вариант мендосинского двигателя заключив в прозрачную вакуумную капсулу кольцевой супермаховик и нанеся на его поверхность фотопоглощающее покрытие — и получив сразу еще и аккумулятор, а не только двигатель?
Кроме того обычный супермаховик как то его автор стабильно подвешивал на магнитах
(http://n-t.ru/ri/gl/ek08.htm).
Vjatcheslav3345
28.03.2016 09:51Вот здесь, на разрезе, можно посмотреть на подвес некольцевого, существующего "в железе" супермаховика (http://www.kinetic-power.com/kinetic).

theambient
28.03.2016 12:29Статья читается на одном дыхании, спасибо за прекрасное изложение. К своему стыду с логарифмом я не угадал =)
Можете пояснить, почему в примере с палкой вы строите потенциальное поле вот так
def system_potential(x,y): return unit_potential(0,1,x,y)+unit_potential(0,-1,x,y) def energy(x,y): return system_potential(x+2,y)+system_potential(x-2,y)
То есть почему вы на каждом конце палки сверху и снизу ставите по заряду? Вы ведь строите суммарное поле всей системы и должны получить 4 (неустойчивых) максимума, но в вершинах креста, а не прямоугольника. Вот тут я что-то недопонимать.
haqreu
28.03.2016 12:46Подождите, два заряда, что поставлены вертикально, у меня фиксированы. Они создают потенциал с двумя пиками, расположенными вертикально. Так? Возьмём один свободный заряд (левый конец палки) и нарисуем карту его потенциальной энергии. Это будет просто copy-paste карта потенциала, единственное, что она будет чуточку сдвинута по горизонтали, т.к. я рисую карту относительно не самого заряда, а центра палки. Сделаем то же самое с правым зарядом, опять получим карту, сдвинутую по горизонтали, но уже в другую сторону.
Карта энергии всей палки — это сумма двух карт энергий её концов. Четыре пика по углам прямоугольника.

RomanVZ
29.03.2016 23:04+1Можно взять висмут или пиролитический графит, чтоб обойтись без боковой опоры. Пассивная левитация, без электромагнитов и сверхпроводников.
В принципе, можно не мудрить с фотоэлементами, достаточно свойств графита:

qwertyk06
30.03.2016 01:49Согласно википедии диамагнетики позволяют обойти теорему Ирншоу… Но должен отметить что для всех видео приведённых вами здесь и найденных мной левитируют крайне небольшие предметы (жаба это максимум, да и то там БОЛЬШОЕ поле вызванное явно не магнитом) кубики, шарики, графитовый стержень и тп (над весьма массивныеми субъектами).
С другой стороны в первичном видео сказано что давление на боковую стенку не более грамма. Так что ждём точно такой же системы с большим кирпичом сбоку (диамагнетик) и магнитом на конце (вместо опоры). Может кто и осилит, только смысла нет, при попытках снятия энергии тут вам и трение будет и магнит в диамагнетик упрётся и ещё 31 удовольствие.
- два магнита повернутые одним полюсом друг к другу, будучи не закрепленными будут стремиться:


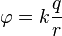
pda0
Насчёт века это трудно сразу сказать, фотоэлементы могут раньше деградировать. :) Магниты постоянные могут потерять свойства.
haqreu
Вообще в статье речь шла не совсем о том.