Троичные вычисления
Я готовлю курс лекций по архитектуре компьютеров для студентов нашего университета, и в качестве небольшой практической разминки я бы хотел предложить студентам построить примитивный программируемый вычислитель в троичной логике. Конкретно эта статья рассказывает про базовый модуль, который будет использоваться в постройке, а именно про троичный мультиплексор. В данном тексте я не пойду дальше простейшего сумматора (и его реализации в железе), текст и так получается достаточно насыщенным. В последующих статьях я буду потихоньку рассказывать, куда меня эта кривая заведёт, так как я в самом начале авантюры.
- Считаем до трёх: раз
- Считаем до трёх: два
Я выбрал сбалансированную троичную систему, в которой один трит может представлять одно из трёх значений -1, 0 или 1. Весьма подробно о ней можно почитать тут.
На любые вопросы из разряда «зачем?!» я отвечаю заранее: «Because I can».

Стройматериал: троичный мультиплексор
Логический уровень
Базовым стройматериалом является троичный мультиплексор. Логически это штука о пяти выводах: на один из них (sel) подаётся троичный сигнал селектора, и в зависимости от него на выход мультиплексора (out) подаётся один из трёх входных сигналов inN, inO или inP.
На схемах его обычно рисуют как-то так:

Демультиплексор работает похожим образом: в зависимости от селектора один вход замыкается на один из трёх выходов. Та железка, что использую я, имеет двунаправленные ключи, так что она разом и мультиплексор, и демультиплексор (впрочем, возможности демультиплексирования я пока не использую).
Реализация в железе
Дизайн железки принадлежит Александру Шабаршину, я его честно целиком свистнул. Единственное, что я сделал, так это развёл железку под поверхностный монтаж, т.к. эти микросхемы существенно дешевле выводных, в китае можно их взять по 50 центов за штуку.

До того, как я наткнулся на этот дизайн (к слову, немало информации по троичным вычислениям и железкам для них есть на форуме Александра), я пытался городить огород из cd4016 и cd4007, что работало, но было крайне громоздко и неудобно. Использование ключей dg403 даёт настоящий троичный элемент без какой бы то ни было избыточности типа кодирования троичной системы в двухбитовой двоичной.
Кстати, в отличие от многих теоретиков, Александр пошёл гораздо дальше, он разработал и заказал собственные микросхемы, работающие на троичной логике:

Для создания одного мультиплексора TRIMUX Александр использовал две микросхемы ключей dg403, у одной логика запитана между -5В и 0В, а у второй между 0В и 5В, что позволяет работать с троичным сигналом, представленным тремя уровнями напряжения -5, 0 и 5В. Но это оставляет половину ног свободной, поэтому в две микросхемы dg403 как раз умещаются два троичных мультиплексора.

Как это использовать? Функции одного аргумента
Давайте пропустим тривиальную тождественную функцию, которую можно получить, подав на соответствующие входы мультиплексора -1, 0, 1.
Для начала давайте прибавим ко входному сигналу А единицу (разумеется, в кольце -1,0,1):
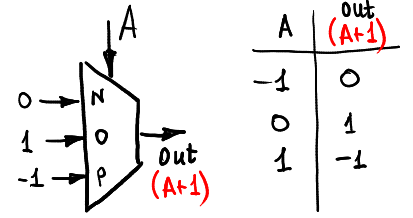
А вот так мы можем единицу вычесть:
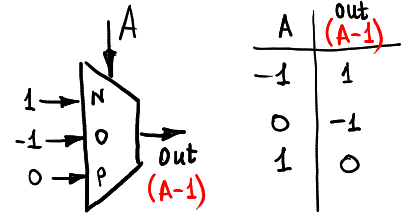
Вот так мы можем посчитать функцию одного аргумента max(A,0):
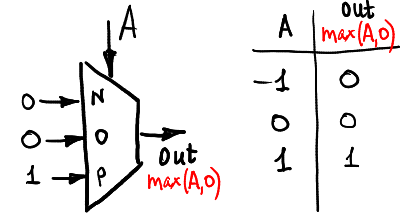
А вот так min(A,0):

Функции двух аргументов: полусумматор
A+B
Итак, одного мультиплексора нам хватает для того, чтобы посчитать функцию одного аргумента. Чтобы посчитать функцию двух аргументов, придётся использовать три или четыре мультиплексора. Например, если мы хотим посчитать сумму двух троичных сигналов A и B (по-прежнему в рамках кольца -1,0,1), то можно использовать такую схему:
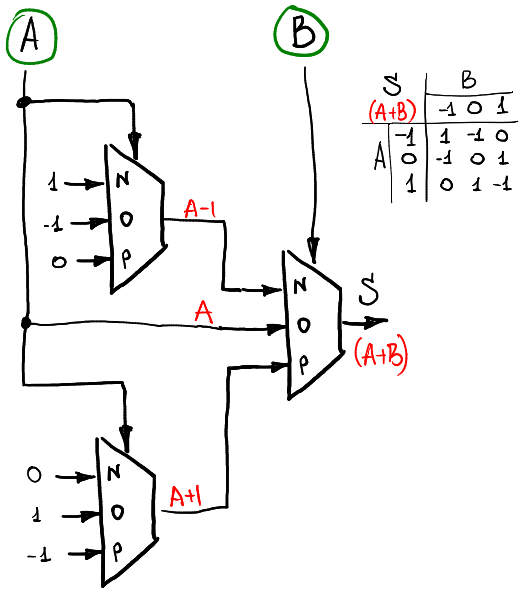
Первый уровень мультиплексоров считает функции одного аргумента от сигнала А, а второй их использует в зависимости от уровня сигнала B.
Консенсус
Если мы хотим посчитать функцию консенсуса от двух троичных сигналов (она равна -1 если A=B=-1 и равна 1 если A=B=1, иначе она равняется нулю), то это можно сделать так:

Реализация в железе
Итак, мы только что создали полусумматор. В зависимости от двух входов А и B он выдаёт два выхода S и С, которые можно посчитать как A+B = S + 3*C.
Давайте его тестировать! Красный диод = -1, выключенный = 0, зелёный = 1. Таким образом, эта фотография нам говорит, что S=-1, C=1, то есть, 1+1 = -1 + 3*1:

Вот эта табличка даёт все девять возможных состояний нашего полусумматора, каждая ячейка приводит соответствующие значения S и С. По ссылкам в ячейках соответствующие фотографии железа.
| S,C | B | |||
| -1 | 0 | 1 | ||
| A | -1 | 1,-1 | -1,0 | 0,0 |
| 0 | -1,0 | 0,0 | 1,0 | |
| 1 | 0,0 | 1,0 | -1,1 | |
Функции трёх аргументов: полный сумматор
Полный же сумматор должен принимать на вход три аргумента, а не два, как полусумматор. Третьим аргументом является перенос из младшего разряда. Итак, из трёх входов A,B и Cin нам нужно посчитать два выхода S и Cout по закону A+B+Cin = S + 3*Cout.
Сумма трёх тритов
Для функции трёх аргументов идея ровно та же, что и для функции двух: мы применяем послойную подготовку данных для последующих вычислений. То есть, первый слой мультиплексоров принимает на вход только A, второй только B и последний мультиплексор только Cin.
Вот так может выглядеть схема вычисления S:
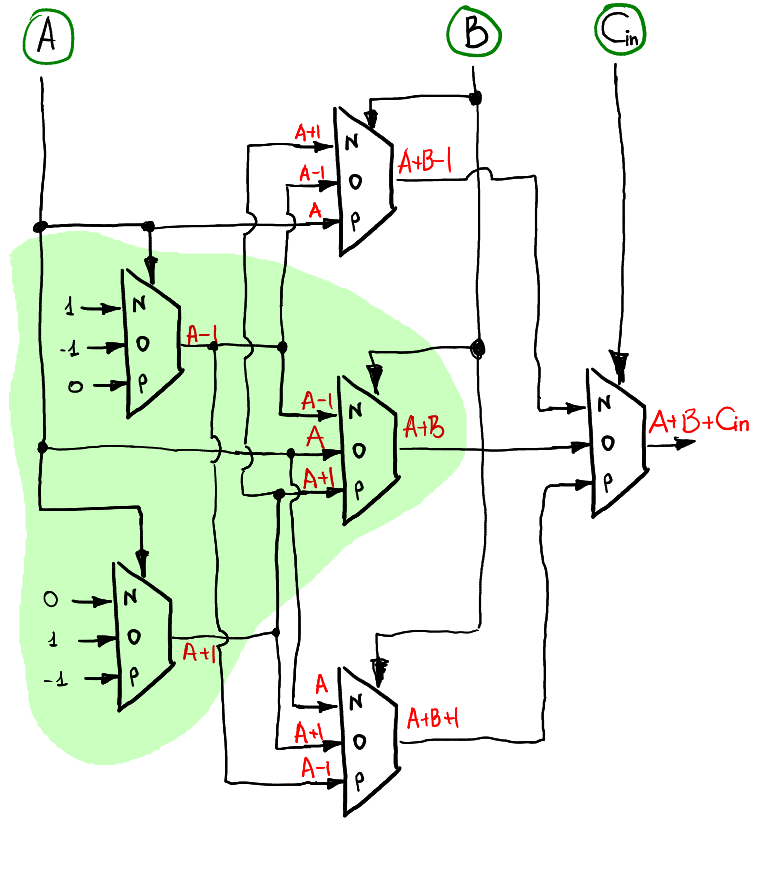
Обратите внимание, что когда Cin = 0, то это по факту должно повторять работу полусумматора. Логично, что полусумматор входит в схему полного сумматора (выделено зелёным).
Переполнение результата
Трит переполнения считается совершенно аналогично и совершенно так же схема включает в себя схему вычисления трита переполнения у полусумматора:

Реализация в железе
В этот раз тыкать проводочки на макетке мне было лень, поэтому быстренько развёл плату:

И сдул вековую пыль с запасов гетинакаса:

Вот все 27 возможных состояний полного сумматора, обратите внимание, что средняя таблица (которая для Cin=0) повторяет таблицу для полусумматора.
| Cin = -1 | B | |||
| -1 | 0 | 1 | ||
| A | -1 | 0,-1 | 1,-1 | -1,0 |
| 0 | 1,-1 | -1,0 | 0,0 | |
| 1 | -1,0 | 0,0 | 1,0 | |
| Cin = 0 | B | |||
| -1 | 0 | 1 | ||
| A | -1 | 1,-1 | -1,0 | 0,0 |
| 0 | -1,0 | 0,0 | 1,0 | |
| 1 | 0,0 | 1,0 | -1,1 | |
| Cin = 1 | B | |||
| -1 | 0 | 1 | ||
| A | -1 | -1,0 | 0,0 | 1,0 |
| 0 | 0,0 | 1,0 | -1,1 | |
| 1 | 1,0 | -1,1 | 0,1 | |
Чем хорош полный сумматор, так это тем, что такие платы можно собирать в бутерброд до достижения нужной разрядности.
Вот так выглядит бутерброд для двух разрядов:

Вот так он решает пример -4 + 2 (левая плата — младший разряд):

На самом деле, конечно, для самого младшего разряда нам не нужен полный сумматор, полусумматора вполне хватило бы, ведь нам не нужно делать перенос на вход сумматора младешго разряда. Но полусумматор на макетке я уже разобрал, и мне лень его собирать обратно :)
Заключение
В данной статье я кратко рассказал, из чего и как можно строить базу для троичных вычислений. В следующих выпусках ждите счётчики, память, АЛУ и т.п. Stay tuned!
Комментарии (63)
DrPass
16.03.2017 03:57Мне кажется, в аппарате явно недостаточно светодиодов, показывающих состояние полусумматоров. По крайней мере, если вы его собрали для показа студентам на лекциях, а не исключительно for fun.

haqreu
16.03.2017 09:13Я не показываю конечную железку, у меня её нет. Но вообще для понимания состояний есть моделирование, это быстрее и эффективнее, нежели провода перетыкать на макетах.
DrPass
16.03.2017 12:12Но вообще для понимания состояний есть моделирование, это быстрее и эффективнее
Тут больше психологический эффект. Студентам просто интереснее, когда им показываешь живой работающий макет, а не софтинку на лабораторном компьютере.
haqreu
16.03.2017 12:14Потому и делаю железку. Но железка нужна для проверки результатов моделирования, а не наоборот.

zelyony
16.03.2017 05:58+1если студенты разобрались с двоичными мультиплексорами, то зачем им еще забивать голову (некоторые просто зубрят не понимая) троичными? какой бонус? повторение — мать учения? какие практические применения у троичной логики? да даже если оно есть, не лучше ли потратить это время на изучение более универсальных FPGA, OpenCL, что уж точно не будет лишним в их будущем?
а если они не разобрались с двоичными, то нахера усложнять троичными?
На любые вопросы из разряда «зачем?!» я отвечаю заранее: «Because I can».
ощущение, что вы для себя "for fun" создали троичные хреньки, а теперь нескольким потокам (не на один ведь год) будете втюхивать с гордостью свою работу студентам. хорошо, когда твоя работа не пропала даром? но нужно ли "забивать" этим студентов? cui bono?

Ovsiannikov
16.03.2017 06:24+11Так автор же в университете преподаёт, а не в ПТУ. Если кто-то не может разобраться с университетским курсом, то может они не там учится, и ему стоит пойти в учебное заведение рангом пониже?

zelyony
16.03.2017 06:36+1в моем комменте дело было не в "кому преподавать?", а "что преподавать?"
я ведь не знаю всех нюансов:
- можно троичные мультиплексоры подать за одну пару, а можно растянуть на полсеметра. во втором случае резонный вопрос: может заменить на что-то более полезное для будущих спецов?
- и если автор говорит, что "оно студентам НАДО", у меня вообще нет вопросов

haqreu
16.03.2017 09:07+27Зарекался я не отвечать на вопрос «зачем», но один раз всё же сделаю. Разобью по пунктам:
1. В университете (даже на специальности информатика) преподают не только OpenCL, но и литературу, философию и физическую культуру. Поэтому утверждение «лучше бы» неуместно без контекста, который вы не знаете.
2. В университете уместно преподавать не только будущее технологий, но также и прошлое, развивая кругозор и создавая полную картину окружающей среды. Да, я планирую сделать расширение памяти для ATMEL AVR на ферритовых кольцах и опять-таки показать его студентам.
3. Большинство моих студентов никогда в жизни не задавалось вопросом, есть ли жизнь за пределами двоичной системы. Просто даже не подозревают, что можно делать иначе.
4. Вы сильно недооцениваете «for fun». Приносить развлечение и элемент игры в курс лекций я просто обязан, иначе никто меня реально слушать не будет.
VLT
16.03.2017 10:07+6Спасибо Вам что вы есть, что есть такие преподаватели которые стремятся? донести интересно.

Calc
16.03.2017 11:52+2Не обращайте внимания на этих людей.
Нам в техникуме преподавали полностью всю железную часть с проектированием.
Слышали о двоичных системах, троичных, 17ричных, 13 ричных (в институте максимум двоичная, 8 и 16 были)
Память на ферритовых кольцах — вообще отдельная тема. Мало кто из ныне живущих специалистов слышал о ней, а видели еще меньше. (мне 30 лет)
Так что много от преподавателя зависит, а не от места обучения.
haqreu
16.03.2017 11:59+2Пожалуйста, не принимайте моё использование слова «университет» как снобизм. Я вовсе не собирался принижать другие учебные заведения. Я говорил об обучении в целом, а университет указал просто как то место, где конкретно я работаю.

AnROm
16.03.2017 16:09Большинство моих студентов никогда в жизни не задавалось вопросом, есть ли жизнь за пределами двоичной системы. Просто даже не подозревают, что можно делать иначе.
Мои ровесники на работе не имеют даже минимальных знаний и представления о троичной с.с. У нас в универе рассказывали о ней, но практики не было. В принципе, если учебное время позволяет, то почему бы и нет.

dronab
17.03.2017 11:21Я в одно время хотел собрать на SMD транзисторах простейшую двоичную логику — типо 4 битный проц, 512 байт оперативки, ПЗУ. По сути аналог микроконтроллера на дискретных элементах. Для реализации на нем программы которая будет запрашивать с современной микросхемы RTC дату и время и выводить на 7-ми сегментные индикаторы. Причем монтаж планировался ультра плотный — все компоненты близко друг другу, платы тонкие, между плат расстояние плотное с изолирующим слоем, минимум разъемов или очень мелкие.
Сил, терпения и быть может мозгов не хватило. Пока отложил до лучших времен.
Vjatcheslav3345
21.03.2017 12:31-2- Большинство моих студентов никогда в жизни не задавалось вопросом, есть ли жизнь за пределами двоичной системы. Просто даже не подозревают, что можно делать иначе.
А доводится ли до конца этот методический пример по обучению самостоятельному мышлению? — т. е. даются ли студентам самостоятельные задания или рефераты на тему "провести расследования и выяснить — почему троичная система пока не вышла за рамки лабораторий" (тут правильный ответ нужно будет искать вообще вне этой системы — кто сумел выйти из рамок — тот и умеет мыслить самостоятельно).

SergLens
23.03.2017 18:41-1Почти не знаком со всеми этими системами. Но недавно подумал именно как Вы — почему двоичность, почему — правда и ложь? Ведь всем же известно, что истина — где-то посередине — а для этого всё-таки подходит троичная система. Успехов в исследовании!

ivkomn
16.03.2017 16:18...(некоторые просто зубрят не понимая)...
Когда в инсте на Каширке учился, была байка, что «такие инженеры стране не нужны» :)
mayorovp
16.03.2017 08:00Как упражнение для ума — сойдет, но в получившейся "железной" схеме явно избыточное число элементов. Все мультиплексоры, принимающие на вход константы, наверняка можно было бы сделать проще.

haqreu
16.03.2017 09:09+1Вы предлагаете удешевление ценой усложнения понимания схемы. Иметь один-единственный блок, с которым можно работать, имеет своё преимущество. Каждый пусть ищет свой личный компромисс. Не забывайте, что я делаю не серийную, а демонстрационную железку.

Arastas
16.03.2017 23:38А на 4х мультиплексорах можно собрать универсальную схему, реализующая любую функцию двух аргументов. Но на трёх смотрится красивее. :)

ij_king
16.03.2017 08:42-1Отличная идея!!! Давайте соберём команду, подключим аксакалов из МГУ (Хосе Рамиля Альвареса и Маслова Сергея Петровича) и сделаем новую вычислительную вселенную!!! :)
nerudo
16.03.2017 08:44Как представляется число 42 (и -42) в троичной логике?

Akon32
16.03.2017 08:58+542_10=(81-27-9-3)_10 = (+1;-1;-1;-1;0)_3
-42_10 = (-1;+1;+1;+1;0)_3
SpyDeX
16.03.2017 10:22Первый раз вижу систему счисления с отрицательными базовыми значениями.
сколько знаю, в основе числа от 0 до (base-1). // двоичная, восьмиричная, десятичная, шестнадцатиричная и прочие.
Очень необычно и очень смущает.
haqreu
16.03.2017 10:27+4Это очень удобно, т.к. органично представляет отрицательные числа. Нет мутных вещей типа отрицательных нулей и все счётчики-сумматоры могут сразу считать в обе стороны.

pehat
17.03.2017 02:04+1Не надо тёплое с мягким путать.
1) Отрицательные нули — это мутная вещь арифметики с плавающей точкой. Как в троичной логике реализовать числа, у которых будет одинаковое число знаков после запятой вне зависимости от порядка? Придётся городить абсолютно такой же костыль, как в IEEE 754.
2) Вообще-то в двоичной арифметике всё и так считается в обе стороны, просто это арифметика по модулю 2^[количество_бит_на_число]. Вся фигня с дополнительным кодом — иллюзия для белковых субъектов, которым понадобилось вывести на печать вычет.Zenitchik
17.03.2017 09:53Как в троичной логике реализовать числа, у которых будет одинаковое число знаков после запятой вне зависимости от порядка?
А в чём Вы видите трудность? Отрицательных нулей не появится, так же, как и не потребуется дополнительный код (вообще).

tyomitch
23.03.2017 11:10-1Вообще-то в двоичной арифметике всё и так считается в обе стороны, просто это арифметика по модулю 2^[количество_бит_на_число]. Вся фигня с дополнительным кодом — иллюзия для белковых субъектов, которым понадобилось вывести на печать вычет.
На самом деле нет: если предположить 8-битную арифметику, то- для беззнаковых чисел: 128 ? 2 = 256 = 1'0
- для знаковых чисел: 128 ? 2 = -256 = 255'0
mayorovp
23.03.2017 11:29А, вы наверное про операции mul и imul, которые перемножают два числа и возвращают число удвоенной разрядности.
Так вот — в большинстве ЯП нет способа получить старшую часть результата этой операции без хитрых обходных путей (вызовов внешних функций или интринсиков). А для младшего разряда утверждение о том, что это всего лишь операция в кольце вычетов выполняется (в обоих случаях получен корректный 0).
А всяческие обходные пути с получением старшей части числа используются, за редкими исключениями, лишь для реализации арифметики повышенной разрядности. Для которой, если ее разрядность ограничена, продолжает выполняться это условие.

igormu
16.03.2017 10:39+4Есть еще, например, система счисления по основанию (-2) и по любым другим отрицательным основаниям.
Есть по основанию фи.
Есть на основе чисел Фибоначчи. Много их.

Mimizavr
16.03.2017 09:32+1Огромное спасибо за статью. Когда-то в институте у меня была возможность заняться как раз устройствами на троичной логике. А я, дурак, забил(((
Если я не ошибаюсь, то даже есть пример реализации операционной системы для троичного компьютера.

k_simakov
16.03.2017 12:48Подскажите, а что из себя представляет блок питания в вашей железной реализации? Любопытно больше деталей узнать о том, как вы получаете -5, 0 и +5.

haqreu
16.03.2017 12:51Пока что у меня тупой делитель на резисторах, видите крокодилы с блока питания? Я туда 10 вольт подаю. А потом делитель, который даст среднюю точку.
Когда будет надо больший ток иметь, то поставлю два китайских зарядника на 5В.
GarryC
16.03.2017 13:30+2По поводу «Сетуни» — она не была троичной в истином смысле этого слова, там трит реализовывался на двух битах, поэтому по энергетике она выигрывала не так, как должна была, то есть почти не выигрывала.
Поскольку хорошего троичного элемента так и не сделали, проект умер естественной смертью.
И по поводу троичной системы вообще — личо мне кажется, что главная проблема тут в третьем значении, в предложеной автором реализации, например, будет крайне сложно отличить настоящий ноль от короткого замыкания плюс и минут единицы.
MaM
16.03.2017 14:32Как я читал, в Сетуни, таки использовалась память на ферритовых кольца, насчет энергетики не знаю, но где-то слышал, что она выигрывала надежностью и как не парадоксально, надежность её и погубила, заводам просто было не выгодно производить Сетунь. Относительно ламп, ферритовые кольца все-же более надежный элемент. Ваши последние строчки вызывают у меня недоумение, а как обычный вентиль его заметит? Тут уже вопрос к хорошей конструкции. Есть зоны значений, есть фарбайден зоны, в компьютере таки логический ноль, это не отсутствие напряжение, а вполне определенный (низкий) уровень напряжения. Если вам интересно Xаррис и Харрис можете почитать. (тут я про двоичную конечно, как верно заметил potan в троичной делают по другому)
DrPass
16.03.2017 14:57+3надежность её и погубила, заводам просто было не выгодно производить Сетунь
Да в СССР хозрасчета в те годы не было, у заводов с этим было проще, исходили из заявок и госплана. Скорее, заказчики осторожничали с машинами непривычной конструкции.
GarryC
17.03.2017 09:02+2Память на ферритах применялась и вполне себе для двоичной логики ( например в «Электроника-100И» ) — 2 уровня намагничивания, а отсутствие намагничивания просто не использовалось. Да и перекинуть колечко из одного состояния в другое очень просто — достаточно дать ток с запасом и кривая намагниченности сработает за Вас, а вот остановится ровно посередине весьма и весьма нетривиальная задача.
А насчет уровня — речь не о вентиле, который любой уровень воспримет как ноль или единицу, а про человека с тестером или с индикатором — вот там то мы можем увидеть разницу в напряжении при закоротке в двоичной логике, а в троичной в данной реализации это весьма затрудненно.

potan
16.03.2017 14:15+4Представление троичного сигнала уровнями напряжения — очевидное, но не совсем правильное решение. Оно будет проигрывать двоичной логике.
Основная проблема — большая разница напряжений между крайними значениями.
Более эффективно передавать троичное значение по трем проводам (на двух низкое, на одном высокое напряжение). Это соотносится с передачей двоичного значения по дифференциальной паре, которое достаточно широко используется. При этом сохраняется помехозащищенность двоичного кодирования, сокращается количество аппаратуры и глубина схем (за счет троичной системы) и сокращается энергопотребление, так как на каждом такте надо перезарядить меньшее количество линий.
Еще такое кодирование хорошо для реализации асинхронной логики (неготовое значение кодируется низким уровнем на всех линиях).
Плюс — можно использовать стандартные элементы.

NikLok
16.03.2017 19:33Брусенцов Н П в последней реализации логического элемента использовал двухполярный источник питания. 0 соответствовал 0. + соответствовал 1, а минус соответствовал -1. И схема была чем-то типа сбалансированного моста.

vlad230596
19.03.2017 12:11Спасибо большое за статью, и в особенности, за кучу поясняющих картинок. Вы не зря выбрали путь преподавателя, читать такую статью очень приятно. Более того, всё понятно, даже если не вчитываться в текст, а только пробежаться по графическому материалу.

FlameStorm
21.03.2017 14:33Статья хорошая, спасибо.
Иллюстрации схем и понятные технические решения очень хороши. Успехов в популяризации и обучение свежих светлых голов!
Пробежал по комментам, поискал на всякий случай ссылку и не нашёл, так что добавлю — загляните на trinary.ru, лет наверное пять назад для себя открыл. До сих пор помню, уникальная инфа и люди.
«Троичные» часы вообще вещь, которая должна быть у любого сурового программера :)
И по схемотехнике ребята помнится там тоже решали вопросы, может быть полезно.
Akon32
23.03.2017 13:07+1Эти часы http://trinary.ru/projects/sinchron/?
А в чём они троичные? Синусоида и есть синусоида.
FlameStorm
23.03.2017 18:02Ну я потому и взял слово «троичные» в кавычки, т.к. сам не понял, почему же они троичные. Но необычные и любопытные это точно.


Psychosynthesis
Круто!
Не сочтите за троллинг, но есть ли какие-нибудь реально целесообразные применения у итогового девайса на подобной схеме?
SpyDeX
Когда я был маленьким, нам на курсах тоже пытались рассказать про троичную систему с перспективой построения компьютеров на такой логике. Половина одногрупников была восторжена «потенциалом мощности» таких решений(этож сразу на 50% мощнее чем двоичная логика!).
Прошло 20 лет, готовятся всё те же курсы, для таких же студентов.
Так что перспектива такая — лет через 20, какой-нибудь из восторженых текущей лекцией студентов снова будет готовить точно такую-же лекцию для следующей партии студентов.
Других применений я не предполагаю, ну ещё может несколько человек в порывах научного голода попробует какую-нибудь мигалку светодиодов собрать.
MaM
Сетунь.
pehat
Сетунь — машина с троичной логикой на двоичной элементной базе. Товарищ Брусенцов взял два бита и комбинацию 11 запретил. После получения этого знания я долго чесал репу в поисках «увеличения эффективности». Да, такая вещь как дополнительный код исчезла, но в остальном профит сомнителен.
haqreu
У моего девайса применение демонстрационное.
Psychosynthesis
А перспективы?
antstar
Например, для грубой эмуляции работы квантового компьютера. Если в классическом исполнении кубиты принимают конечные значения (0|1) с определенной вероятностью, то здесь конечные состояния можно принять за (-1|1) с вероятностью 100% и с суперпозицией в (0)
TAPAHbl4
Всё же квантовая суперпозиция — это когда сразу во всех значениях, а после измерения — только в одном единственном. В данной ситуации это обыкновенная троичная логика, тут значение будет всегда одно, как до так и после измерения.