Введение

Свёрточные нейронные сети (СНС). Звучит как странное сочетание биологии и математики с примесью информатики, но как бы оно не звучало, эти сети — одни из самых влиятельных инноваций в области компьютерного зрения. Впервые нейронные сети привлекли всеобщее внимание в 2012 году, когда Алекс Крижевски благодаря им выиграл конкурс ImageNet (грубо говоря, это ежегодная олимпиада по машинному зрению), снизив рекорд ошибок классификации с 26% до 15%, что тогда стало прорывом. Сегодня глубинное обучения лежит в основе услуг многих компаний: Facebook использует нейронные сети для алгоритмов автоматического проставления тегов, Google — для поиска среди фотографий пользователя, Amazon — для генерации рекомендаций товаров, Pinterest — для персонализации домашней страницы пользователя, а Instagram — для поисковой инфраструктуры.

Но классический, и, возможно, самый популярный вариант использования сетей это обработка изображений. Давайте посмотрим, как СНС используются для классификации изображений.

Задача

Задача классификации изображений — это приём начального изображения и вывод его класса (кошка, собака и т.д.) или группы вероятных классов, которая лучше всего характеризует изображение. Для людей это один из первых навыков, который они начинают осваивать с рождения.

Мы овладеваем им естественно, без усилий, став взрослыми. Даже не думая, мы можем быстро и легко распознать пространство, которое нас окружает, вместе с объектами. Когда мы видим изображение или просто смотрим на происходящее вокруг, чаще всего мы можем сразу охарактеризовать место действия, дать каждому объекту ярлык, и все это происходит бессознательно, незаметно для разума. Эти навыки быстрого распознавания шаблонов, обобщения уже полученных знаний, и адаптации к различной запечатлённой на фото обстановке не доступны нашим электронным приятелям.

Вводы и выводы

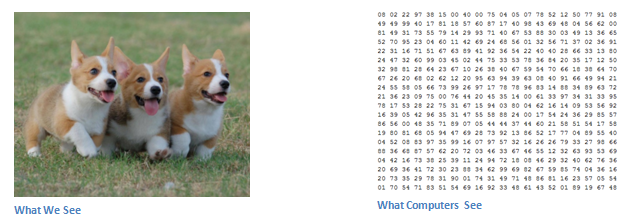
Когда компьютер видит изображение (принимает данные на вход), он видит массив пикселей. В зависимости от разрешения и размера изображения, например, размер массива может быть 32х32х3 (где 3 — это значения каналов RGB). Чтобы было понятней, давайте представим, у нас есть цветное изображение в формате JPG, и его размер 480х480. Соответствующий массив будет 480х480х3. Каждому из этих чисел присваивается значение от 0 до 255, которое описывает интенсивность пикселя в этой точке. Эти цифры, оставаясь бессмысленными для нас, когда мы определяем что на изображении, являются единственными вводными данными, доступными компьютеру.  Идея в том, что вы даете компьютеру эту матрицу, а он выводит числа, которые описывают вероятность класса изображения (.80 для кошки, .15 для собаки, .05 для птицы и т.д.).

Чего мы хотим от компьютера

Теперь, когда мы определили задачу, ввод и вывод, давайте думать о том, как подбираться к решению. Мы хотим, чтобы компьютер мог различать все данные ему изображения и распознавать уникальные особенности, которые делают собаку собакой, а кошку кошкой. У нас и этот процесс происходит подсознательно. Когда мы смотрим на изображение собаки, мы можем отнести его к конкретному классу, если у изображения есть характерные особенности, которые можно идентифицировать, такие как лапы или четыре ноги. Аналогичным образом компьютер может выполнять классификацию изображений через поиск характеристик базового уровня, например границ и искривлений, а затем с помощью построения более абстрактных концепций через группы свёрточных слоев. Это общее описание того, что делают СНС. Теперь перейдём к специфике.

Биологические связи

В начале немного истории. Когда вы впервые услышали термин сверточные нейронные сети, возможно подумали о чем-то связанном с нейронауками или биологией, и отчасти были правы. В каком-то смысле. СНС — это действительно прототип зрительной коры мозга. Зрительная кора имеет небольшие участки клеток, которые чувствительны к конкретным областям поля зрения. Эту идею детально рассмотрели с помощью потрясающего эксперимента Хьюбел и Визель в 1962 году (видео), в котором показали, что отдельные мозговые нервные клетки реагировали (или активировались) только при визуальном восприятии границ определенной ориентации. Например, некоторые нейроны активировались, когда воспринимали вертикальные границы, а некоторые — горизонтальные или диагональные. Хьюбел и Визель выяснили, что все эти нейроны сосредоточены в виде стержневой архитектуры и вместе формируют визуальное восприятие. Эту идею специализированных компонентов внутри системы, которые решают конкретные задачи (как клетки зрительной коры, которые ищут специфические характеристики) и используют машины, и эта идея — основа СНС.

Структура

Вернёмся к специфике. Что конкретно делают СНС? Берётся изображение, пропускается через серию свёрточных, нелинейных слоев, слоев объединения и полносвязных слоёв, и генерируется вывод. Как мы уже говорили, выводом может быть класс или вероятность классов, которые лучше всего описывают изображение. Сложный момент — понимание того, что делает каждый из этих слоев. Так что давайте перейдем к самому важному.

Первый cлой — математическая часть

Первый слой в СНС всегда свёрточный. Вы же помните, какой ввод у этого свёрточного слоя? Как уже говорилось ранее, вводное изображение — это матрица 32 х 32 х 3 с пиксельными значениями. Легче всего понять, что такое свёрточный слой, если представить его в виде фонарика, который светит на верхнюю левую часть изображения. Допустим свет, который излучает этот фонарик, покрывает площадь 5 х 5. А теперь давайте представим, что фонарик движется по всем областям вводного изображения. В терминах компьютерного обучения этот фонарик называется фильтром (иногда нейроном или ядром), а области, на которые он светит, называются рецептивным полем (полем восприятия). То есть наш фильтр — это матрица (такую матрицу ещё называют матрицей весов или матрицей параметров). Заметьте, что глубина у фильтра должна быть такой же, как и глубина вводного изображения (тогда есть гарантия математической верности), и размеры этого фильтра — 5 х 5 х 3. Теперь давайте за пример возьмем позицию, в которой находится фильтр.  Пусть это будет левый верхний угол. Поскольку фильтр производит свёртку, то есть передвигается по вводному изображению, он умножает значения фильтра на исходные значения пикселей изображения ( поэлементное умножение). Все эти умножения суммируются (всего 75 умножений). И в итоге получается одно число. Помните, оно просто символизирует нахождение фильтра в верхнем левом углу изображения. Теперь повторим этот процесс в каждой позиции. (Следующий шаг — перемещение фильтра вправо на единицу, затем еще на единицу вправо и так далее). Каждая уникальная позиция введённого изображения производит число. После прохождения фильтра по всем позициям получается матрица 28 х 28 х 1, которую называют функцией активации или картой признаков. Матрица 28 х 28 получается потому, что есть 784 различных позиции, которые могут пройти через фильтр 5 х 5 изображения 32 х 32. Эти 784 числа преобразуются в матрицу 28 х 28.

(Небольшая ремарка: некоторые изображения, в том числе то, что вы видите выше, взяты из потрясающей книги "Нейронные сети и глубинное обучение" Майкла Нильсена ("Neural Networks и Deep Learning", by Michael Nielsen). Настоятельно рекомендую).

Допустим, теперь мы используем два 5 х 5 х 3 фильтра вместо одного. Тогда выходным значением будет 28 х 28 х 2.

Первый слой

Давайте поговорим о том, что эта свертка на самом деле делает на высоком уровне. Каждый фильтр можно рассматривать как идентификатор свойства. Когда я говорю свойство, я имею в виду прямые границы, простые цвета и кривые. Подумайте о самых простых характеристиках, которые имеют все изображения в общем. Скажем, наш первый фильтр 7 х 7 х 3, и он будет детектором кривых. (Сейчас давайте игнорировать тот факт, что у фильтра глубина 3, и рассмотрим только верхний слой фильтра и изображения, для простоты). У фильтра пиксельная структура, в которой численные значения выше вдоль области, определяющей форму кривой (помните, фильтры, о которых мы говорим, это просто числа!).                 

Вернемся к математической визуализации. Когда у нас в левом верхнем углу вводного изображения есть фильтр, он производит умножение значений фильтра на значения пикселей этой области. Давайте рассмотрим пример изображения, которому мы хотим присвоить класс, и установим фильтр в верхнем левом углу.

Помните, всё что нам нужно, это умножить значения фильтра на исходные значения пикселей изображения.

По сути, если на вводном изображении есть форма, в общих чертах похожая на кривую, которую представляет этот фильтр, и все умноженные значения суммируются, то результатом будет большое значение! Теперь давайте посмотрим, что произойдёт, когда мы переместим фильтр.

Значение намного ниже! Это потому, что в новой области изображения нет ничего, что фильтр определения кривой мог засечь. Помните, что вывод этого свёрточного слоя — карта свойств. В самом простом случае, при наличии одного фильтра свертки (и если этот фильтр — детектор кривой), карта свойств покажет области, в которых больше вероятности наличия кривых. В этом примере в левом верхнем углу значение нашей 28 х 28 х 1 карты свойств будет 6600. Это высокое значение показывает, что, возможно, что-то похожее на кривую присутствует на изображении, и такая вероятность активировала фильтр. В правом верхнем углу значение у карты свойств будет 0, потому что на картинке не было ничего, что могло активировать фильтр (проще говоря, в этой области не было кривой). Помните, что это только для одного фильтра. Это фильтр, который обнаруживает линии с изгибом наружу. Могут быть другие фильтры для линий, изогнутых внутрь или просто прямых. Чем больше фильтров, тем больше глубина карты свойств, и тем больше информации мы имеем о вводной картинке.

Ремарка: Фильтр, о котором я рассказал в этом разделе, упрощён для упрощения математики свёртывания. На рисунке ниже видны примеры фактических визуализаций фильтров первого свёрточного слоя обученной сети. Но идея здесь та же. Фильтры на первом слое сворачиваются вокруг вводного изображения и "активируются" (или производят большие значения), когда специфическая черта, которую они ищут, есть во вводном изображении.

(Заметка: изображения выше — из Стэнфордского курса 231N, который преподают Андрей Карпатый и Джастин Джонсон (Andrej Karpathy and Justin Johnson). Рекомендую тем, кто хочет лучше изучить СНС).

Идём глубже по сети

Сегодня в традиционной сверточной нейронной сетевой архитектуре существуют и другие слои, которые перемежаются со свёрточными. Я очень рекомендую тем, кто интересуется темой, почитать об этих слоях, чтобы понять их функциональность и эффекты. Классическая архитектура СНС будет выглядеть так:

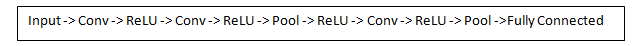
Последний слой, хоть и находится в конце, один из важных — мы перейдём к нему позже. Давайте подытожим то, в чём мы уже разобрались. Мы говорили о том, что умеют определять фильтры первого свёрточного слоя. Они обнаруживают свойства базового уровня, такие как границы и кривые. Как можно себе представить, чтобы предположить какой тип объекта изображён на картинке, нам нужна сеть, способная распознавать свойства более высокого уровня, как например руки, лапы или уши. Так что давайте подумаем, как выглядит выходной результат сети после первого свёрточного слоя. Его размер 28 х 28 х 3 (при условии, что мы используем три фильтра 5 х 5 х 3).  Когда картинка проходит через один свёрточный слой, выход первого слоя становится вводным значением 2-го слоя. Теперь это немного сложнее визуализировать. Когда мы говорили о первом слое, вводом были только данные исходного изображения. Но когда мы перешли ко 2-му слою, вводным значением для него стала одна или несколько карт свойств — результат обработки предыдущим слоем. Каждый набор вводных данных описывает позиции, где на исходном изображении встречаются определенные базовые признаки.

Теперь, когда вы применяете набор фильтров поверх этого (пропускаете картинку через второй свёрточный слой), на выходе будут активированы фильтры, которые представляют свойства более высокого уровня. Типами этих свойств могут быть полукольца (комбинация прямой границы с изгибом) или квадратов (сочетание нескольких прямых ребер). Чем больше свёрточных слоёв проходит изображение и чем дальше оно движется по сети, тем более сложные характеристики выводятся в картах активации. В конце сети могут быть фильтры, которые активируются при наличии рукописного текста на изображении, при наличии розовых объектов и т.д. Если вы хотите узнать больше о фильтрах в свёрточных сетях, Мэтт Зейлер и Роб Фергюс написали отличную научно-исследовательскую работу на эту тему. Ещё на ютубе есть видео Джейсона Йосински c отличным визуальным представлением этих процессов.

Еще один интересный момент. Когда вы двигаетесь вглубь сети, фильтры работают со все большим полем восприятия, а значит, они в состоянии обрабатывать информацию с большей площади первоначального изображения (простыми словами, они лучше приспособляются к обработке большей области пиксельного пространства).

Полносвязные слои

Теперь, когда мы можем обнаружить высокоуровневые свойства, самое крутое — это прикрепление полносвязного слоя в конце сети. Этот слой берёт вводные данные и выводит N-пространственный вектор, где N — число классов, из которых программа выбирает нужный. Например, если вы хотите программу по распознаванию цифр, у N будет значение 10, потому что цифр 10. Каждое число в этом N-пространственном векторе представляет собой вероятность конкретного класса. Например, если результирующий вектор для программы распознавания цифр это [0 0,1 0,1 0,75 0 0 0 0 0,05], значит существует 10% вероятность, что на изображении "1", 10% вероятность, что на изображение "2", 75% вероятность — "3", и 5% вероятность — "9" (конечно, есть и другие способы представить вывод).

Способ, с помощью которого работает полносвязный слой — это обращение к выходу предыдущего слоя (который, как мы помним, должен выводить высокоуровневые карты свойств) и определение свойств, которые больше связаны с определенным классом. Например, если программа предсказывает, что на каком-то изображении собака, у карт свойств, которые отражают высокоуровневые характеристики, такие как лапы или 4 ноги, должны быть высокие значения. Точно так же, если программа распознаёт, что на изображении птица — у неё будут высокие значения в картах свойств, представленных высокоуровневыми характеристиками вроде крыльев или клюва. Полносвязный слой смотрит на то, что функции высокого уровня сильно связаны с определенным классом и имеют определенные веса, так что, когда вы вычисляете произведения весов с предыдущим слоем, то получаете правильные вероятности для различных классов.

Обучение (или "Что заставляет эту штуку работать")

Это один из аспектов нейронных сетей, о котором я специально до сих пор не упоминал. Вероятно, это самая важная часть. Возможно, у вас появилось множество вопросов. Откуда фильтры первого свёрточного слоя знают, что нужно искать границы и кривые? Откуда полносвязный слой знает, что ищет карта свойств? Откуда фильтры каждого слоя знают, какие хранить значения? Способ, которым компьютер способен корректировать значения фильтра (или весов) — это обучающий процесс, который называют методом обратного распространения ошибки.

Перед тем, как перейти к объяснению этого метода, поговорим о том, что нейронной сети нужно для работы. Когда мы рождаемся, наши головы пусты. Мы не понимаем как распознать кошку, собаку или птицу. Ситуация с СНС похожа: до момента построения сети, веса или значения фильтра случайны. Фильтры не умеют искать границы и кривые. Фильтры верхних слоёв не умеют искать лапы и клювы. Когда мы становимся старше, родители и учителя показывают нам разные картинки и изображения и присваивают им соответствующие ярлыки. Та же идея показа картинки и присваивания ярлыка используется в обучающем процессе, который проходит СНС. Давайте представим, что у нас есть набор обучающих картинок, в котором тысячи изображений собак, кошек и птиц. У каждого изображения есть ярлык с названием животного.

Метод обратного распространения ошибки можно разделить на 4 отдельных блока: прямое распространение, функцию потери, обратное распространение и обновление веса. Во время прямого распространения, берётся тренировочное изображение — как помните, это матрица 32 х 32 х 3 — и пропускается через всю сеть. В первом обучающем примере, так как все веса или значения фильтра были инициализированы случайным образом, выходным значением будет что-то вроде [.1 .1 .1 .1 .1 .1 .1 .1 .1 .1], то есть такое значение, которое не даст предпочтения какому-то определённому числу. Сеть с такими весами не может найти свойства базового уровня и не может обоснованно определить класс изображения. Это ведёт к функции потери. Помните, то, что мы используем сейчас — это обучающие данные. У таких данных есть и изображение и ярлык. Допустим, первое обучающее изображение — это цифра 3. Ярлыком изображения будет [0 0 0 1 0 0 0 0 0 0]. Функция потери может быть выражена по-разному, но часто используется СКО (среднеквадратическая ошибка), это 1/2 умножить на (реальность — предсказание) в квадрате.

Примем это значение за переменную L. Как вы догадываетесь, потеря будет очень высокой для первых двух обучающих изображений. Теперь давайте подумаем об этом интуитивно. Мы хотим добиться того, чтобы спрогнозированный ярлык (вывод свёрточного слоя) был таким же, как ярлык обучающего изображения (это значит, что сеть сделала верное предположение). Чтобы такого добиться, нам нужно свести к минимуму количество потерь, которое у нас есть. Визуализируя это как задачу оптимизации из математического анализа, нам нужно выяснить, какие входы (веса, в нашем случае) самым непосредственным образом способствовали потерям (или ошибкам) сети.

(Один из способов визуализировать идею минимизации потери — это трёхмерный график, где веса нейронной сети (очевидно их больше, чем 2, но тут пример упрощен) это независимые переменные, а зависимая переменная — это потеря. Задача минимизации потерь — отрегулировать веса так, чтобы снизить потерю. Визуально нам нужно приблизиться к самой нижней точке чашеподобного объекта. Чтобы добиться этого, нужно найти производную потери (в рамках нарисованного графика — рассчитать угловой коэффициент в каждом направлении) с учётом весов).

Это математический эквивалент dL/dW, где W — веса определенного слоя. Теперь нам нужно выполнить обратное распространение через сеть, которое определяет, какие веса оказали большее влияние на потери, и найти способы, как их настроить, чтобы уменьшить потери. После того, как мы вычислим производную, перейдём к последнему этапу — обновлению весов. Возьмём все фильтровые веса и обновим их так, чтобы они менялись в направлении градиента.

Скорость обучения — это параметр, который выбирается программистом. Высокая скорость обучения означает, что в обновлениях веса делались более крупные шаги, поэтому образцу может потребоваться меньше времени, чтобы набрать оптимальный набор весов. Но слишком высокая скорость обучения может привести к очень крупным и недостаточно точным скачкам, которые помешают достижению оптимальных показателей.

Процесс прямого распространения, функцию потери, обратное распространение и обновление весов, обычно называют одним периодом дискретизации (или epoch — эпохой). Программа будет повторять этот процесс фиксированное количество периодов для каждого тренировочного изображения. После того, как обновление параметров завершится на последнем тренировочном образце, сеть в теории должна быть достаточно хорошо обучена и веса слоёв настроены правильно.

Тестирование

Наконец, чтобы увидеть, работает ли СНС, мы берём другой набор изображений и ярлыков и пропускаем изображения через сеть. Сравниваем выходы с реальностью и смотрим, работает ли наша сеть.

Как компании используют СНС

Данные, данные, данные. Компании, у которых тонны этого шестибуквенного магического добра, имеют закономерное преимущество перед остальными конкурентами. Чем больше тренировочных данных, которые можно скормить сети, тем больше можно создать обучающих итераций, больше обновлений весов и перед уходом в продакшн, получить лучше обученную сеть. Facebook (и Instagram) могут использовать все фотографии миллиарда пользователей, которые у них сегодня есть, Pinterest — информацию из 50 миллиардов пинов, Google — данные поиска, а Amazon — данные о миллионах продуктов, которые ежедневно покупаются. И теперь вы знаете какое волшебство они используют в своих целях.

Ремарка 

Хоть этот пост и должен быть хорошим началом для понимания СНС, это не полный обзор. К моментам, которые не обсуждались в этой статье, относятся нелинейные (nonlinear) слои и слои объединения (pooling), а также гиперпараметры сети, такие как размеры фильтров, шаги и отступы. Сетевая архитектура, пакетная нормализация, исчезающие градиенты, выпадение, методы инициализации, невыпуклая оптимизация, сдвиг, варианты функций потерь, расширение данных, методы регуляризации, машинные особенности, модификации обратного распространения и много других необсуждённых (пока ;-) тем.

(Перевод Наталии Басс)